基于改进经验公式的油浸式变压器热点温度计算
2022-10-11亢银柱晋涛牛曙李国栋阮江军邓永清
亢银柱,晋涛,牛曙,李国栋,阮江军,邓永清
(1.国网山西省电力公司电力科学研究院, 太原 030001; 2.武汉大学 电气与自动化学院, 武汉 430072)
0 引 言
变压器绕组热点温度是影响变压器绕组油纸绝缘老化程度的重要因素,分析变压器的热特性对保障变压器运行安全性与可靠性具有重要意义[1-2]。将光纤温度传感器安装在变压器绕组线饼中或绕组附近可能发生过热的位置,可对变压器热点温度进行直接测量[3-4],但该方法只适用于新制造的变压器,同时敷设传感器时需要对外壳进行打孔,可能会造成变压器油渗漏和潮湿环境下测温油槽进水并积聚的后果。变压器热点温度瞬态计算经验公式法简化了变压器运行过程中复杂的内部传热过程,将变压器绕组热点温度等效为环境温度、变压器内部顶油温升和热点对内部顶油的温升之和,具有实现简单易行、适用范围广的特点,因此通过监测变压器顶层油温,进而结合经验公式推算变压器绕组热点温度在实际工程中得到广泛应用。
针对不同负载容量的油浸式变压器的热点温度计算导则于上世纪八十年代初步形成[5-6],经过多次扩充完善,目前国内较为常用的为 IEEE Standard C57.91-2011[7]和GB/T 1094.7-2008(对应IEC 60076-7:2005)[8-9]。经验公式为运行变压器绕组热点温度的监测提供了一个有效手段,但经验公式在考虑其他环境因素如风速、湿度等情况下的热点温度计算结果与测量结果误差较大[10],如何提高经验公式计算变压器热点温度时的计算精度一直是经验公式在实际应用中所需关心的问题[11]。国内外学者对标准推荐热点温度计算经验公式的适应性以及改进方法进行了大量的研究。文献[12]对IEEE Annex G推荐的经验公式展开了研究,分析了经验公式中特征参数对变压器热点温度计算结果的影响,研究结果表明标准推荐的特征参数仅适用于正常运行情况下的变压器热点温度计算,若发生过负荷或欠负荷情况,计算误差较大。文献[13]对IEEE的推荐公式做出了改进,考虑了温升过程中顶层油温的变化,并有改进后的公式对三相不平衡负载情况下的油浸式变压器温升进行计算,计算结果与实测结果的温差小于0.5 ℃。文献[14]根据变压器热点温度、负载电流和环境温度等监测数据,采用遗传算法对IEEE推荐公式中的变压器热力学参数进行修正,提高了经验公式的计算精度。文献[15]通过对35台退役变压器的环境温度、负荷、热力学特性等参数统计,给出了IEC 60076-7中热点系数的计算方法,研究结果说明标准中给出的热点系数普遍偏低,并根据统计结果改进了推荐经验公式。文献[16]根据变压器铁心和绕组的发热过程,详细解释了GB/T 15164-1994中推荐的绕组热点温度计算方程各参数项的含义,并对推荐方程中的绕组指数和油指数项进行了调整和修改,使得经验公式具有更高的可靠性。
配电变压器是电网的重要组成部分,随着国家节能减排政策的落实,S13节能型变压器在电网中得到了越来越广泛的应用[17-18]。为分析S13-M-100 kVA/10 kV型变压器的热特性,对一台S13-M-100 kVA/10 kV型变压器进行了多负载率并考虑风速作用的变压器温升试验,温升试验中在变压器绕组中安装荧光式光纤温度传感器来测量变压器绕组热点温度,采用热电阻温度传感器来测量变压器顶层油温和外界环境温度。结合温升试验结果,针对GB/T 1094.7—2008中推荐瞬态热点温度计算经验公式在负荷大幅下降以及环境中有风速作用时计算误差较大的情况,提出了修正因子,并使用Levenberg-Marquardt(L-M)算法对变压器热特性参数和风速修正因子参数进行估算,改进了油浸式变压器绕组热点温度经验公式计算方法。
1 变压器多负载率温升试验
1.1 试验平台及测温点布置
选用的试验变压器为额定容量100 kVA、额定电压10 000±2×2.5%/400 V的S13-M-100 kVA/10 kV 三相三柱式平面叠铁芯变压器,结构如图1所示。

图1 S13-M-100 kVA/10 kV平面叠铁芯变压器
温升试验中采用FTM-6CH-H200荧光式光纤测量变压器绕组温升,该光纤测温系统的量程为-40 ℃~200 ℃,温度采集间隔为1 s,精度为±0.1 ℃。本次试验在变压器绕组上安装了6根FTM-6CH-H200型号荧光式光纤测温传感器。6根光纤测温仪依次布置于A、B、C相高压绕组以及低压绕组间的油道中,如图2所示,为了使得光纤探头测量所得温度更贴近绕组热点温度,光纤测温传感器安装在绕组95%高度处,即最有可能是绕组热点的位置,试验中取最高的光纤探头温度做为绕组热点温度。

图2 光纤安装示意图
本次试验采用PT100型热电阻测量变压器顶层油温和环境温度。温升试验中,热电阻测温探头和光纤探头测得的温度信号在数字式显示器集成后,由RS 232传输到电脑控制端,因此可以通过软件平台实时对各热电阻测温探头以及光纤测温数据进行监视,热电阻和光纤的测控平台如图3所示。

图3 热电阻和光纤测温平台
1.2 变压器温升试验
采用短路法对S13-M-100 kVA/10 kV三相三柱立体变压器进行温升试验,试验接线图和现场图如图4和图5所示。

图4 变压器温升试验原理图

图5 变压器温升试验现场图
温升试验之前首先进行了变压器在额定条件下的空载和负载试验,确定该变压器空载损耗为149.2 W,负载损耗为1517.3 W。多阶段试验通过电源给变压器三相绕组加载不同损耗,不同负载率条件下变压器损耗计算公式为:
P=n2×Pk+P0
(1)
式中n为变压器负载率;Pk为负载损耗;P0为空载损耗。
试验中考虑了环境中风速的作用。风速分为1 m/s、 2 m/s、 3 m/s三档,风速通过调节试验风扇的档位和距变压器的距离进行控制,风速通过手持式风速仪进行测量,如图6所示。变压器依次加载0.8倍、1.1倍、0.9倍、0.7倍、1.2倍、1.0倍的载荷,进行稳态温升试验,保持负载及风速不变直至变压器各个测温点的温度达到稳定,每种负载率稳态试验耗时约6 h。

图6 试验风扇和风速仪
2 变压器绕组瞬态热点温度优化计算方法
2.1 标准经验公式瞬态热点温度计算
对于油浸自冷式变压器,GB/T 1094.7-2008中推荐的指数方程法经验公式中,不同负载系数下的热点温度等于环境温度、顶层油温升和变压器热点温度与顶层油温之间的温差三者之和,热点温度上升时和热点温度下降时的指数方程法经验公式分别为:
(2)
f3(t)+HgrKy
(3)
式中θα为环境温度;Δθoi为变压器初始顶层油温升;Δθor为额定损耗下变压器顶层油温升;Δθhi为变压器热点温度与顶层油温的初始梯度;R为额定电流下负载损耗和空载损耗比值;K为变压器运行负载系数;x为变压器油指数;H为热点系数;gr为额定电流下绕组平均温度对油平均温度的梯度;y为绕组指数;f1(t)、f2(t)和f3(t)均为时间的指数函数,用于表达油浸式变压器瞬态绕组热点温度随变压器负载持续时间的变化关系,三者的表达式为:
f1(t)=1-e-t/(k11×τ0)
(4)
f2(t)=k21×(1-e-t/(k22×τW))-(k21-1)×(1-e-t/(τ0/k22))
(5)
f3(t)=e-t/(k11×τ0)
(6)
其中,常数k11、k21、k22和常数τo、τw均为变压器的热特性参数;τo为变压器平均油时间常数(min);τw为变压器绕组热点位置的时间常数(min)。对于不同容量等级和不同散热方式的油浸式变压器,标准给出的热特性参数推荐值如表1所示。

表1 油浸式变压器热特性参数推荐值
使用GB/T 1094.7-2008标准推荐的经验公式对变压器绕组热点温度进行计算,变压器瞬态热点温度计算结果与试验结果如图7所示。
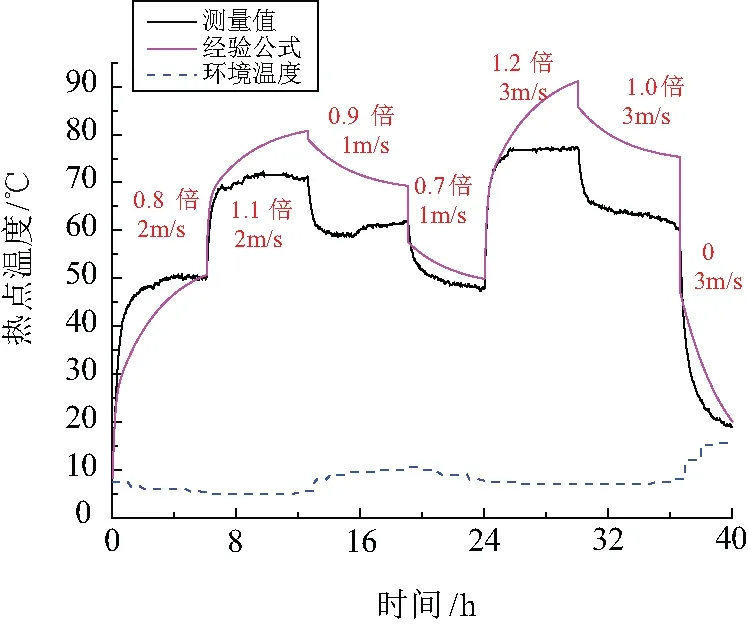
图7 热点温度计算结果与试验结果对比
图7中可以看出,由于经验公式法无法考虑环境中风速对变压器热点温升的影响,在约40 h的负载和风速共同波动的温升过程中,不同风速情况下标准推荐经验公式计算结果与试验结果之间具有较大误差,其中1.2倍负载电流情况下, 3 m/s的风速导致热点降温达16 ℃。因此考虑风速作用时,有必要对标准中变压器热点温度计算经验公式进行修正。
2.2 改进瞬态热点温度计算经验公式
直接利用标准经验公式对变压器瞬态热点温度计算在外界环境风速较大时出现了较大误差,这是由于标准经 验公式只考虑了环境温度和变压器负载率,没有计及风速对变压器热点温度的影响,基于此,引入风速修正因子,对标准经验公式进行改进,即增加修正项e-kv,因此有考虑风速的变压器在不同负载下的顶层油温对环境温升为:
(7)
式中v为环境风速;k为风速修正因子参数。
考虑风速的变压器在不同负载下的热点温度对顶层油温温升为:
HgrKy×e-k·v
(8)
在变压器负荷下降幅度较大时,直接用标准推荐经验公式对的热点温度计算也具有较大误差,这是由于热点温度下降时,标准经验公式中只考虑了稳态的热点对油温升,而没有考虑负荷下降时的热点对油温升随时间的变化,因此引入负荷下降时初始时刻热点对油温升与稳态热点对油温升的温差(Δθhi-HgrKy×e-kv),并考虑时间因子f4(t),因此得到改进后的负荷上升和负荷下降时的变压器瞬态热点温度计算公式分别如式(9)和式(10)所示:

(9)
(10)
其中:
f4(t)=e-t/τw
(11)
2.3 基于L-M算法参数优化的变压器瞬态热点温度计算
经验公式法计算变压器瞬态热点温度的关键在于选取准确的变压器特性参数,标准中仅仅根据变压器容量及散热方式给出了推荐值。但是实际中由于生产过程中工艺的差异性、变压器结构的复杂性以及环境参数的不确定性,标准中给出的特性参数参考值往往无法精确描述变压器内部绕组、油流、外壳、散热器与环境之间的散热过程,因此需针对具体变压器型号,选用最合适的变压器特性参数。
L-M法是最有效的非线性模型参数估计方法之一,通过寻求多变量函数的最小值进行迭代,其有效结合了最速下降法和高斯牛顿法的优点[19-20]。采用L-M算法,对变压器的瞬态温升数据进行分析,结合优化后的经验公式,对经验公式中描述热点温升过程的变压器特性参数进行寻优,即可获得通过L-M算法优化后的变压器的特性参数。文中变压器特性参数包含变压器热特性参数(k11,k21,k22,τo,τw)以及风速修正因子参数k。变压器的热特性参数描述了变压器绕组与油流热量散失过程的基本特性。
基于L-M算法的变压器特性参数优化过程为:
(1)设试验过程中绕组热点温度与时间以及特性参数的表达式为θh(t)=f(t,α),参数向量α=(k11,k21,k22,τo,τw, k),将变压器热点温度实测数据作为输入(ti,θi),i=1,2,…,n;
(2)根据变压器特性参数推荐值设置初始向量值α0,设置系数β、阻尼因子λ和允许的极小误差值ε,并根据有风和无风条件下多负载温升稳态试验数据确定风速影响因子参数k;

(4)计算雅克比矩阵J(αk),具体表达式如下:
(5)若E(αk)<ε,则αk能够满足辨识需求,迭代结束;否则,以αk+1做为初值来计算误差函数值;
(6)利用式L-M算法迭代表达式计算k+1时刻的参数向量αk+1,具体表达式如下:αk+1=αk-(▽2E(α)+λI)-1J(αk),式中 ▽2E(α)是海森矩阵;λ为阻尼因子;I是单位矩阵;k是迭代次数;J(αk)是E(α)对参数向量αk的雅克比矩阵;
(7)若E(αk+1) (8)迭代结束,得到最优特性参数向量α=(k11,k21,k22,τo,τw, k)的值。 根据上文分析,针对S13-M-100 kVA/10 kV型变压器,采用L-M算法寻优得到的热特性参数和风速修正因子参数取值如表2所示。 表2 L-M算法寻优所得参数 将L-M算法寻优所得特性参数带入改进后的变压器绕组热点温度瞬态计算式,即式(9)和式(10),对S13-M-100 kVA/10 kV变压器温升试验过程中的绕组热点温度进行计算,变压器绕组瞬态热点温度计算结果如图8所示。 图8 热点温度计算结果与试验结果对比 从图8中可以看出,改进后的热点瞬态计算公式与试验结果吻合的较好,在约40 h的负载电流和风速共同波动的温升过程中,变压器绕组热点降温过程的热点温度计算公式引入描述初始状态下绕组热点与顶层油温之间温差及相应的时间因子f4(t)后,利用L-M算法寻优得到的变压器特性参数结合改进经验公式,对变压器的温升过程进行瞬态热点温度计算,结果优于传统的经验公式,改进后的变压器热点温度瞬态计算方法可以更加准确地计算运行中负荷波动、环境温度变化等情况下的变压器热点温度,最大误差不超过5 ℃。 对一台S13-M-100 kVA/10 kV型变压器进行了多负载率并考虑风速作用的变压器温升试验,直接采用经验公式对变压器瞬态热点温度计算在风速为3 m/s时计算值与试验值最大误差达到了16 ℃,通过在经验公式中引入风速修正项和时间因子项改进了经验公式计算方法,使用改进后的经验公式对S13-M-100 kVA/10 kV变压器的多阶段温升试验过程中的绕组热点温度进行计算,同时结合L-M算法对计算中特性参数进行寻优,计算结果与试验结果最大误差不超过5 ℃。研究结果可为变压器在复杂环境下热点温度计算提高参考。

3 结束语
