时间尺度上奇异变质量可控非完整系统的Noether对称性

方 蕊，朱建青

(苏州科技大学数学科学学院，江苏 苏州 215009)

时间尺度是测度链的一种，可以将差分系统与微分系统统一起来进行研究，避免了对于同一问题的重复研究，使得力学系统的研究结果更具有普遍性.目前，时间尺度理论在经济学、物理学等许多领域得到了广泛应用[1-4].在力学系统中，利用对称性导出守恒量是一个比较重要的研究方向，主要通过Noether对称性、Lie对称性和Mei对称性来寻求守恒量[5-12].2008年，Bartosiewicz和Torres给出了时间尺度上Noether定理的一种证明方法[13]；2011年，Bartosiewicz和Torres等给出了时间尺度上Noether定理的另一种证明方法[14].随后，关于时间尺度上对称性的研究取得了一系列重要成果，如：非完整非保守系统的Noether对称性[15]、相空间中非Chetaev型非完整系统的Noether对称性[16]、Lagrange系统的Mei对称性[17]、基于非标准Lagrange函数的动力学系统的Noether对称性[18]、Hergoltz型Hamilton系统的Noether对称性[19]、奇异Chetaev型非完整系统的Lie对称性[20]、二阶线性可控力学系统的Noether对称性[21]及完整非保守力学系统的Noether对称性[22]．

随着航天技术与工业的不断发展，变质量系统的研究日益重要.通常情况下喷气飞机、火箭、航天器等都是变质量系统.近年来，一些学者对于变质量系统的对称性进行了研究并取得了一些成果[23-24].2007年，夏丽莉研究了变质量非完整可控力学系统的统一对称性[25]；2014年，徐超研究了奇异变质量非完整系统的对称性与守恒量[26]；2019年，吴艳研究了时间尺度上变质量系统的对称性理论[27]；2020年，阙朝月研究了时间尺度上变质量非完整系统的Lie对称性与守恒量[28].本文在时间尺度上研究奇异变质量可控非完整系统的Noether对称性与守恒量，给出系统Noether广义准对称性的判据和守恒量，最后对结果的应用举例说明．

1 时间尺度上奇异变质量可控非完整系统的运动方程

假设力学系统的位形由n个广义坐标qs(s=1，2，…，n)确定，mi(i=1，2，…，N)和Δmi分别是第i个质点在t时刻的质量和在时刻t+Δt质点分离(或质点并入)的微粒质量，设时间尺度上质点的质量为

(1)

系统受g个双面理想非Chetaev型非完整约束

s=1，2，…，n;r=1，2，…，b)，

(2)

(3)

时间尺度上的Lagrange函数为

(4)

变质量系统在时间尺度上的Hamilton原理为

(5)

且满足如下的交换关系和端点条件

(6)

δqs(t)|t=t1=δqs(t)|t=t2=0，

(7)

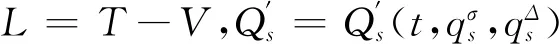
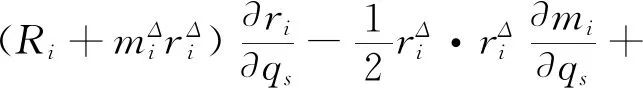
(8)

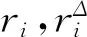
(9)

ui是微粒相对于质点自身的相对速度．

由(5)式可得

(10)

其中，λβ为约束乘子．由(10)式，根据Dubois-Reymond引理可得

(11)

对(11)两边求Δ导数，可得

(12)

令

Λs=λβωβs，

(13)

则方程(12)可表示为

(14)

方程(14)为时间尺度上变质量可控非完整系统的运动方程．

如果

(15)

则将该系统称为时间尺度上奇异变质量可控非完整系统．

因为系统是奇异的，所以仅能解出系统一部分的广义加速度，记为

(s=1，2，…，l，0≤l≤n)，

(16)

则有(n-l)个关系

(k=1，2，…，n-l).

(17)

2 时间尺度上奇异变质量可控非完整系统的Noether对称性与守恒量

在时间尺度上Hamilton作用量为

(18)

引入无限小变换群

(19)

其中ε为无限小参数，ξ0和ξs为生成元．

定义1如果作用量(18)在无限小变换(19)下为广义准对称不变量，即当且仅当对于任意的区间[ta，tb]⊆[t1，t2]，始终成立

(20)

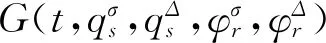
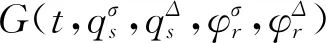
(21)

和限制条件

(22)

其中，

(23)

则将这种不变性称作时间尺度上奇异变质量可控非完整系统的Noether广义准对称性．

定理1对时间尺度上奇异变质量可控非完整系统，如果变换(19)的生成元ξ0和ξs使得广义Noether等式(21)和限制条件(22)成立，则系统的守恒量为

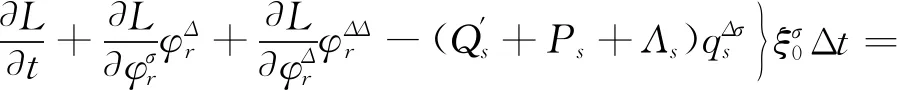
(24)

证明

(25)

推论1当时间尺度T=，非完整约束为Chetaev型且系统非奇异时，根据(21)式可以得到相应经典的广义Noether等式[20]

(26)

根据(24)式可得到相应的守恒量为[20]

(27)

3 算例

例1设时间尺度为

T={2n:n∈}∪{0}.

(28)

系统的Lagrange函数为

(29)

其中,m=m0e-t，m0=const.微粒的绝对速度为零，即

u=-rΔ，

(30)

非势广义力不存在.所受的非完整约束为

(31)

假设(31)为非Chetaev型约束，虚位移的限制方程为

(32)

根据题意可知

P1=P2=0.

(33)

由(12)式可得

(34)

由(29)、(31)、(34)式解出

(35)

可得

(36)

由(21)、(22)式可得

(37)

(38)

由(37)、(38)式可解得系统的生成元为

ξ0=0，ξ1=1，ξ2=1，G=0.

(39)

由定理1可得守恒量为

(40)

例2设时间尺度为

T={2n:n∈}∪{0}.

(41)

系统的Lagrange函数为

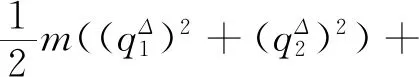
(42)

其中,m=m0e-αt，其中m0，α均为常数，且微粒的绝对速度为零，即

u=-rΔ，

(43)

非势广义力为

(44)

所受非Chetaev型的非完整约束为

(45)

虚位移的限制方程为

(46)

由题可知

P1=P2=P3=0，

(47)

由(12)式，有

(48)

由(42)、(45)、(48)式，有

(49)

可得

(50)

根据(21)、(22)式可得

(51)

(52)

联立方程(51)和(52)，可得到如下解

ξ0=0，ξ1=1，ξ2=1，ξ3=0，

(53)

由定理1可得系统的守恒量为

(54)

4 结论

本文对时间尺度上奇异变质量可控非完整系统的Noether对称性和其相应的守恒量进行了研究.文章基于时间尺度上系统的Hamilton原理，导出系统的运动方程，得到了系统的广义Noether等式和Noether广义准对称性的判据，进而给出守恒量并进行证明.由于时间尺度具有任意性，因此本文结果具有普遍性.本文研究结果可拓展到时间尺度上奇异可控变质量系统的Mei对称性等的研究中．