远程空空导弹角度约束增程弹道制导律研究

张喜豪，张金鹏, 沈 欣

(1. 中国空空导弹研究院，河南 洛阳 471009； 2. 航空制导武器航空科技重点实验室，河南 洛阳 471009; 3.空装驻洛阳地区第一军事代表室，河南 洛阳 471009)

0 引 言

增加射程是空空导弹不断追求的一个方向，在有限尺寸重量约束下，研究如何提高空空导弹的攻击距离具有重要的现实意义。除了从气动布局、 推力系统等方面进行设计外，增程弹道规划及其制导律技术也是实现增程的关键技术之一。弹道规划及其制导律技术应用的范围比较广泛，文献[3]以无人机载空地导弹为对象，提出一种适应复合制导的空地导弹的弹道规划方法，提高无人机载空地导弹的发射距离。文献[4]以高超声速飞行器为对象，提出一种非连续点火助推方案，通过设计增大助推段射程，提高飞行器的射程。文献[5]针对反辐射导弹被动目标定位问题的关键技术研究，提出一种导弹可观测性增强的弹道规划方法，给出了典型非线性滤波器的选取分析。文献[6]研究垂直发射的多导弹系统的高抛弹道协同制导律问题，采用“初+中+末制导”的复合制导方式实现高抛弹道，设计中制导段协同导引律，减少协同攻击网络中各导弹的命中时间差。从弹道规划技术的研究可以看出，其应用与研究对象和研究目的密切相关。本文以空空导弹实现远程精确打击为目的，提出一种适用于远程空空导弹的角度约束增程弹道规划方案，重点研究中制导律，减少导弹飞行过程中的阻力，满足中、 末制导交接班位置、 视线角和入射角等约束条件，达到改善弹道性能的效果。

1 角度约束增程弹道规划方案以及制导律研究

远程空空导弹飞行距离远、 时间长，多采用复合制导系统，典型的复合制导系统由数据链指令修正+捷联式惯性中制导和主动雷达末制导组成。数据链指令修正系统传送载机测量的目标信息，捷联式惯性系统测量导弹信息，由飞控计算机将这些信息进行综合形成中制导控制指令，来控制导弹飞行，然后进入中、 末制导交接班，以便截获目标。截获目标后用主动雷达自寻的系统进行末制导，直至摧毁目标。复合制导系统可以充分发挥不同制导段中不同制导技术的优势，以满足特定的制导需求。

本文在复合制导过程划分的基础上，将远程空空导弹角度约束增程弹道规划为初始段、 爬高段、 成型段和末制导段。角度约束增程弹道规划示意图如图1所示。初始段： 导弹和载机安全分离段，这里不做研究。爬高段： 利用大气密度随高度增加而降低的特性，导弹爬升到一定的高度，避开低空稠密大气而在阻力较小的稀薄大气中飞行，减小飞行过程中空气阻力。成型段： 将导弹制导到期望的中、 末交接班区域，并满足期望的视线角和入射角约束。这里的入射角约束，是约束导引头雷达天线照射目标所发射的入射波与地面的夹角，入射角近似取弹道倾角的绝对值。末制导段： 导弹在完成中、 末制导交接班后进入末制导。爬高段、 成型段和末制导段侧向平面均采用最优制导律，下面根据不同飞行段的需求，研究各阶段纵向平面相关制导律实现问题。

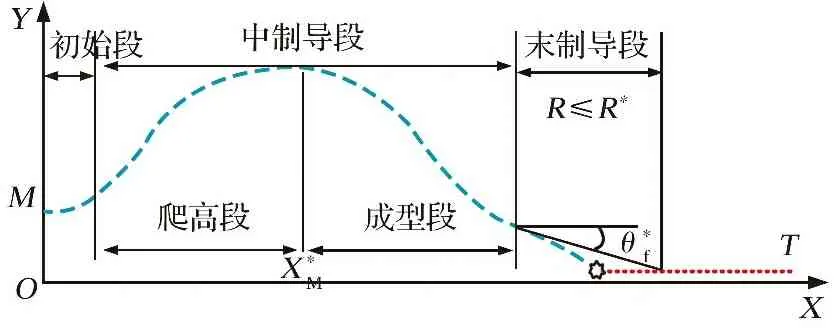
图1 角度约束增程弹道规划示意图

1.1 爬高增程制导律

爬高增程制导律采用过载指令控制，控制爬高段的过载和持续时间，实现中制导阶段导弹的爬高。在文献[12]中EET-2算法的基础上进行改进，考虑导弹当前速度与爬升弹道倾角、 爬升高度的关系，引入速度项对爬高算法进行修正和约束控制，爬高增程制导律为

=(-)-+·cos

(1)

式中：为爬升最佳高度；为导弹当前高度；为导弹当前速度；为当前弹道倾角；为重力加速度。

由式(1)可得，爬升段的弹道倾角变化率为

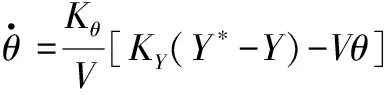
(2)

式中：-为期望高度与当前高度的差值，当前高度离期望高度越远，爬升越快；可以近似看作当前状态高度的可变化量，将此项作为修正项。若当前爬升角较大，此时不宜拉大过载，修正项使得爬升速率降低。爬高弹道通常初始爬升率较大然后逐渐减小，在达到期望高度取到最小值，爬高过程平稳。

1.2 成型角度约束制导律

在中制导结束时，导弹的位置、 速度以及航向等条件应满足中、 末制导交接班的要求。如果一直处于爬高段，则很难达到交接班要求。此外，在打击超低空目标时，地海杂波会导致雷达导引头测量精度下降。研究表明，当导引头入射波以布鲁斯特角入射时，地海杂波的反射系数最小。布鲁斯特角在山地、 平原、 海洋等情况下是不同的，一般在10°～25°之间。因此，角度约束具有重要意义，故研究成型角度约束制导律，把中、 末制导交接班点看作虚拟目标点，将导弹制导到虚拟目标点附近，达到期望的视线角和入射角。

导弹和交接班点相对关系如图2所示。图中，为导弹加速度；为导弹到虚拟目标点的距离；为导弹当前速度矢量和期望末速度矢量之间的角度；为当前速度矢量和导弹与虚拟目标视线之间的角度。

交接班点位置计算：

(3)

式中： (,,)为目标位置信息；,分别为导弹期望的末端倾角和偏角；为制导头截获距离。

图2 导弹与交接班点相对关系

,分别为导弹与交接班点(虚拟目标)距离和相对速度，设相对加速度为控制量，则系统状态方程为

(4)

初始条件为

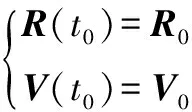
(5)

在此制导律设计中，期望整个飞行过程能量最省，并且末端弹目相对速度矢量()与末端相对位置矢量()满足指定要求。

采用最优控制理论得到满足末端边界条件的制导律。用软惩罚实现在制导律设计中终端边界条件相对重要性的权衡。将此问题的软惩罚定义为

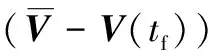
(6)

式中：和为常数，为末端导弹位置与预测交接班点的偏差的权重，为末端相对速度矢量与所需的终端速度矢量之前的偏差的权重。

此最优控制问题性能指标可以描述为

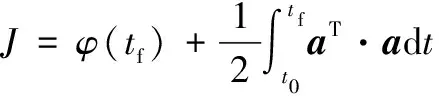
(7)

取此问题的哈密顿函数为

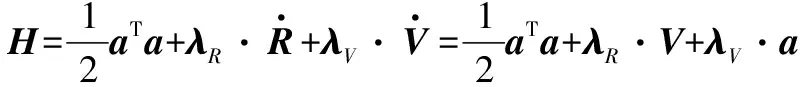
(8)

式中：和为伴随向量。

由最优控制理论可知，有协态方程：

(9)

且伴随向量满足：

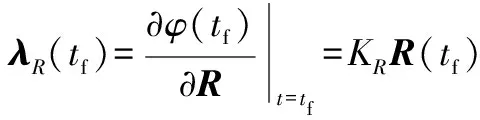
(10)

(11)

将式(11)代入式(9)积分，联立式(10)，可得

()(-)

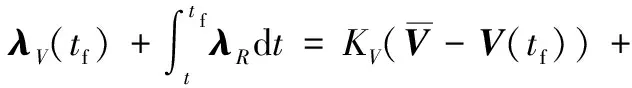
(12)

由最优控制理论的极值条件可知，这里考虑无约束，则有取最小值的必要条件：

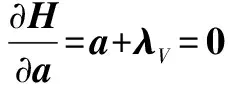
(13)

将式(12) 代入式(13)，可得最优开环控制：

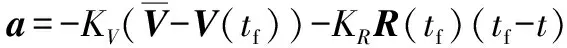
(14)

由相对运动方程可知：

(15)

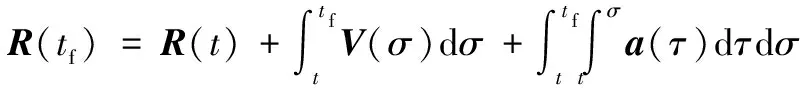
(16)

设零控脱靶量为

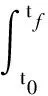
(17)

式中：=-，为剩余飞行时间。

将式(14)代入式(15)积分，与式(17)联立，有

(18)

(19)

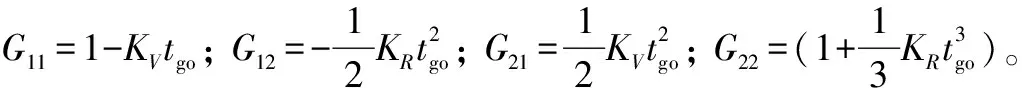
将式(18)求逆，有

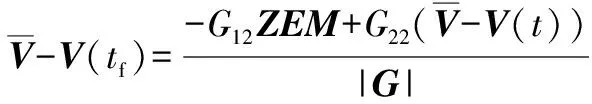
(20)

(21)

将式(20)～(21)代入式(14)可得闭环最优控制：

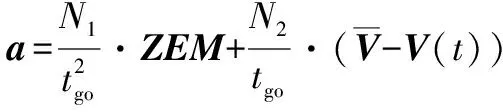
(22)

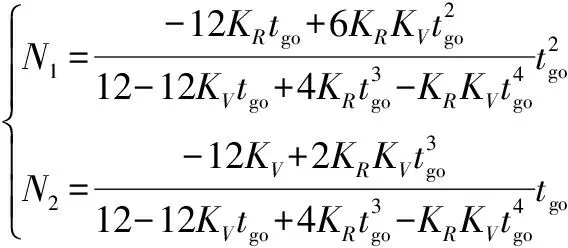
(23)

当取和趋于无穷大，注意到

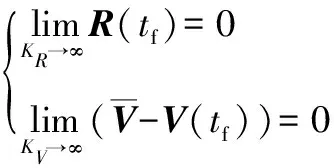
(24)

则有

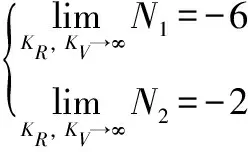
(25)

假设目标加速度为0，结合图2所示的相对运动关系，则可以将式(22)矢量方程转化为标量方程：

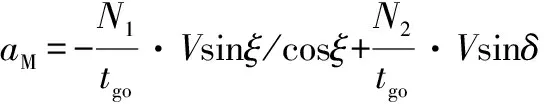
(26)

式中：为法向加速度。

将法向加速度投影到纵向平面, 同时将式(26)中用/替换，可得成型角度约束制导律：

(27)

式中：为法向加速度在纵向平面的投影；为当前位置与交接班点的距离；为导弹期望末速度方向；为相对距离矢量与导弹当前速度矢量的夹角在纵向平面的投影。

1.3 末制导律

末制导采用最优制导律，由导引头提供目标信息，纵向平面的制导律为

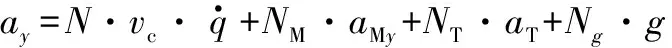
(28)

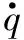
1.4 制导指令交接算法

采用复合制导律设计，各飞行段制导律不同，需要考虑制导指令交接问题。在交接时，开始以前一段加速度指令为主，主导成分逐渐减弱； 然后以后一段加速度指令为主，逐渐增强。优选交接算法如下：

()=2()+[1()-2()]()

(29)

()=(′+-)′，∈[，+′]

(30)

式中：()为交接段加速度指令；1()为前一段制导律在时刻的加速度指令；2()为后一段制导律在时刻的加速度指令；()为一个调节比重的时变系数；为交接段开始时间；′为交接段持续时间。

1.5 制导律参数优化

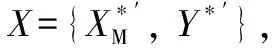
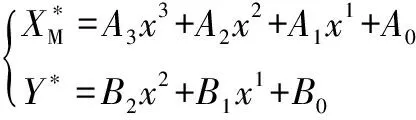
(31)

式中：(=0, 1, 2, 3)和(=0, 1, 2)为多项式拟合得到的系数；为发射距离。

在实际应用中，可以根据不同的发射条件通过式(31)获得当前情况下近似最优的参数，实现增程弹道。

2 仿真验证

以表1中的典型发射条件为例，进行仿真验证，将本文提出的角度约束增程弹道与常规弹道性能对比，常规弹道全程采用最优制导律。

表1 仿真条件

2.1 仿真结果1

在条件1下，针对匀速运动目标，在不同发射距离条件下，采用粒子群优化算法，得到的优化弹道如图3所示，对应的最优参数如表2所示。要求中制导末端弹道倾角约束-10°，弹目距离小于20 km，视为中制导结束，进入末制导阶段。其中双脉冲型发动机第一级和第二级点火间隔时间为12 s，=013,=004。

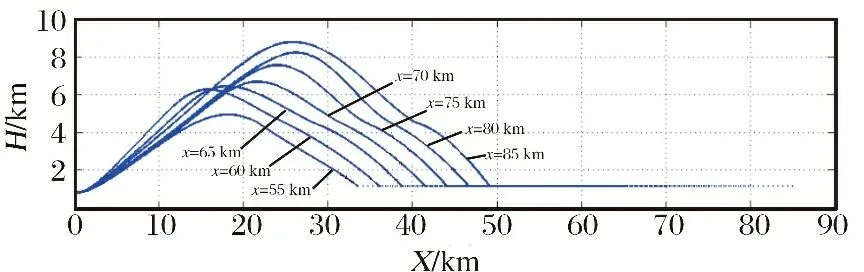
图3 不同发射距离对应的优化弹道

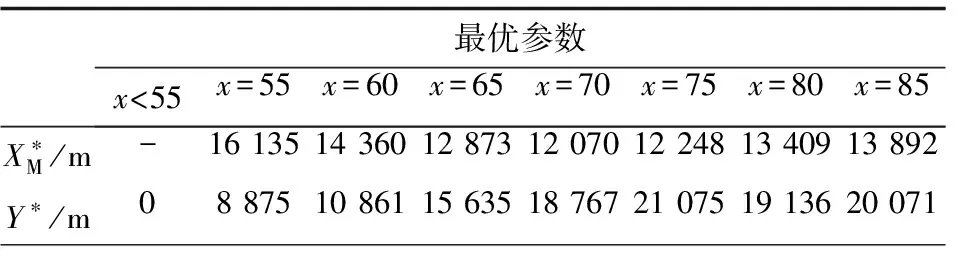
表2 不同发射距离对应的最优参数

2.2 仿真结果2

在条件1下，针对匀速运动目标，发射距离70 km，要求中制导末端弹道倾角约束-10°，弹目距离小于20 km，视为中制导结束，进入末制导阶段。增程弹道爬高段制导律参数：=013，=004，结果如图4(a)～(d)所示。增程弹道和常规弹道在仿真时，都采用双脉冲型发动机，其中第一级和第二级点火间隔时间为12 s，速度变化对比如图4(c)所示。增程弹道在第一级脉冲工作阶段，导弹通过爬高将动能转化为势能储存，飞行速度显著降低； 当第二级脉冲工作时，导弹已飞到约6 km，此时点火可以获得更大的速度增量，相较常规弹道，减少了在低空加速飞行期间空气阻力引起的能量损失。

图4 增程弹道与常规弹道性能对比

图4(a)中点划线部分为中制导结束时导弹位置与目标位置的连线。由图4(b)可知，增程弹道虽然在飞行距离小于2 km时阻力较大，但是通过优化弹道，增大飞行高度，减少了中间段的阻力。从表3对比结果中可以看出，相较于常规弹道，增程弹道末速增加19.19%，增程弹道爬升高度更高，飞行距离更远，平均速度更大，达到了改善弹道性能指标的效果。

2.3 仿真结果3

在条件2下，目标逃逸机动，加速度9.8 m/s，末速不小于350 m/s，最远距离增程弹道与最远距离常规弹道对比结果如图5所示。其中： 末制导距离20 km，弹道倾角约束-10°，双脉冲型发动机第一级和第二级点火间隔时间为20 s。

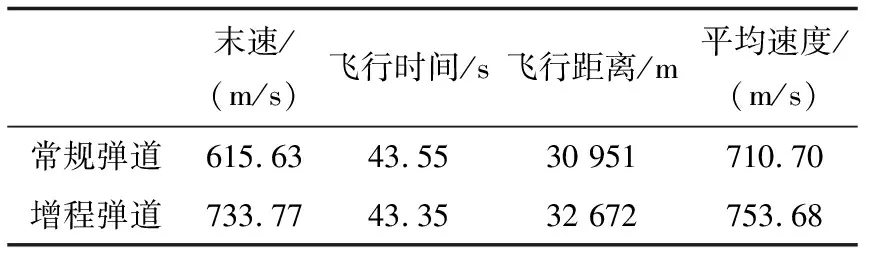
表3 中制导阶段对比

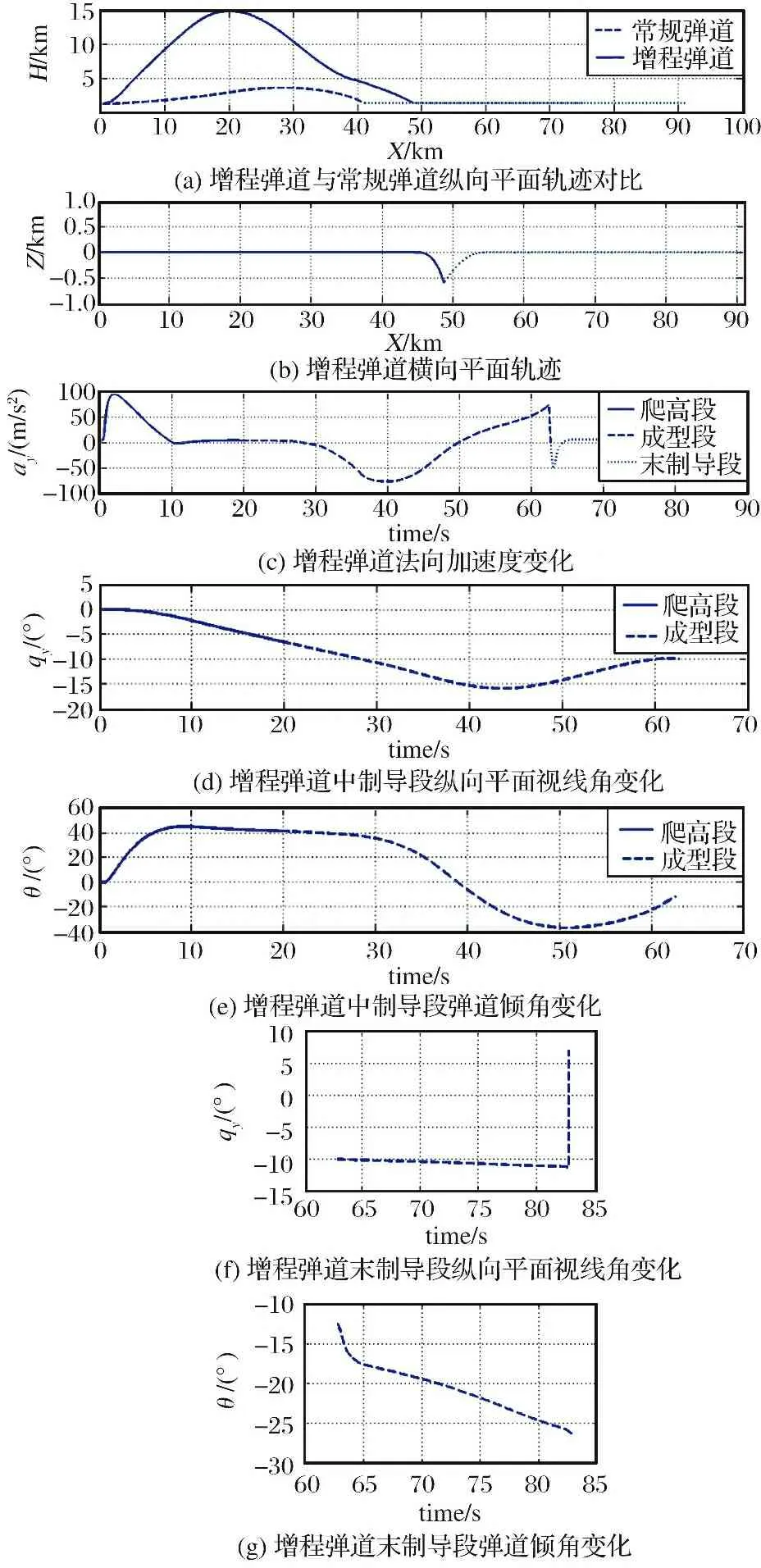
图5 条件2下的最远射程弹道

从加速度变化曲线图5(c)中可以看出，增程弹道在爬高段和成型段，导弹的需用过载较大，最大值不超过98 m/s。增程弹道中、 末制导交接时纵向平面视线角为-10.02°，入射角为12.18°，在末制导阶段视线角变化范围在-10.02°～-11.33°之间，脱靶量为0.401 m。验证了通过设计成型段弹道，中、 末制导交接时，视线角和入射角能达到约束要求。规划成型段弹道还可使得末制导阶段视线角的变化范围比较小，有利于中、 末制导交接班导引头截获目标和末制导阶段稳定跟踪。

在不同的发射条件下，末速不小于350 m/s，增程弹道和常规弹道能够达到的最远距离对比结果如表4所示。可以看出，所提出的增程弹道及其制导律，相对常规弹道及其制导律，增程效果明显。

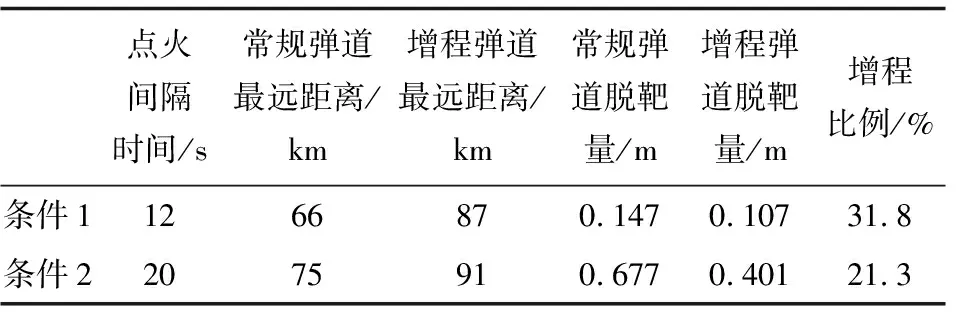
表4 不同条件下的增程效果

3 结 论

本文所提出的对角度约束增程弹道分段规划方案，将复杂的难以求解析解的角度约束增程弹道制导律问题转化为多段复合制导律问题，研究满足不同飞行段要求的制导律，达到实现增程兼角度约束的综合最优。角度约束增程制导律结构简单，弹目制导信息能够获取或估计，便于工程实现； 爬高段弹道显著提高了导弹的最大末速和平均速度，对实现增程效果明显； 成型段弹道能够实现中、 末制导交接班视线角和入射角等约束。所提出的思路和方法对其他战术导弹增程弹道技术的研究也有理论和工程参考价值。实际作战过程中，战场态势更复杂，因此，需要进一步研究导弹离轴发射和不同进入角等情况对增程弹道的影响。