对LFM-Chebyshev混沌二相码信号的干扰仿真分析

宋 泉，张 帆，徐 华

(1. 西南电子设备研究所，成都 610036； 2. 四川省宽带微波电路高密度集成工程研究中心，成都 610036)

0 引 言

随着电子技术的快速发展，电子装备已渗透到军事领域的各个方面，并对武器平台的作战效能起着重要作用。电子战作为现代战争的重要形式具有举足轻重的地位，而电子对抗作为电子战中最重要和最具挑战性的内容，往往伴随着现代雷达的发展而进步，两者相辅相成，共同影响着现代战争的局势和局面。

线性调频信号(LFM)与二进制调相编码信号组合而成的混合信号是一类新出现在雷达中的大时宽-带宽积脉冲压缩信号，这种新型雷达信号的性能关系着电子对抗干扰效能的评估，研究对LFM与二进制调相编码信号组合而成的混合信号的干扰仿真，能丰富电子对抗理论，指导工程应用。这种混合信号具有LFM信号和二进制调相信号两种信号的优点，并且能弥补各自的不足。此外，随着混沌理论的发展，混沌技术逐渐应用于雷达信号处理领域，出现了LFM信号与混沌序列组合的混合雷达信号。由确定性系统产生的混沌二元序列既具有类似噪声的随机性，又具有较好的自相关特性，编码长度不受限制，用混沌序列作为雷达信号具有极强的保密性并且提高了抗干扰的能力。由文献[5-6]可知，在已证明的混沌序列产生的二相码信号中，性能最理想的是由Chebyshev混沌序列产生的二相码。

虽然目前针对常规LFM信号和二相编码信号干扰方法较多，且可达到较好的干扰效果，但是对LFM与二相编码混合信号的干扰研究还不成熟。文献[7]研究了对LFM信号与巴克码混合信号的欺骗干扰效果，但巴克码只有2，3，4，5，7，11，13位七种长度，这在一定程度上限制了其应用。而对LFM与混沌序列组合而成的混合信号的干扰研究较少。

本文在对常规脉冲压缩雷达信号干扰的研究基础上，针对LFM-Chebyshev混沌二相码混合信号特点，仿真了间隔采样转发干扰、 卷积调制干扰、 移频干扰、 距离干扰和距离-移频二维干扰五种典型的干扰方式对这种新型混合信号的干扰效果，同时分析了各种干扰方式的最佳参数设置及相应的干扰效果。

1 LFM-Chebyshev混沌二相码信号数学模型及特点

1.1 混合信号数学模型

LFM-Chebyshev二相码混合信号实质是一种脉内线性调频、 脉间相位编码的信号。脉内线性调频中相邻子脉冲的调频率可以是固定的，也可以是变化的； 脉间的相位编码脉冲是由Chebyshev混沌序列所产生的二相编码。这里考虑脉内线性调频率固定的情况，即每个子脉冲宽度内采用相同的LFM信号。

Chebyshev混沌序列定义为

+1=cos(arccos())

(1)

初始值∈(-1, 1),=4，对初始混沌序列{}=

{,, …，}进行二值化：

(2)

()⊗()

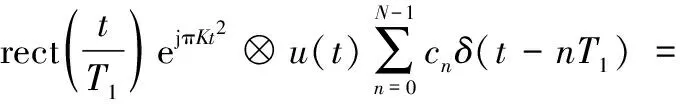
(3)

由匹配滤波理论知，混合信号的匹配滤波器的冲激响应为

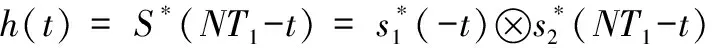
(4)

则匹配滤波器的输出为

()=()⊗()

(5)

由卷积定理有

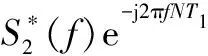
(6)

由式(6)可以看出，混合信号的匹配滤波器输出可以等效为两次脉冲压缩完成。第一次通过LFM信号的匹配滤波器，得到二相编码脉冲信号； 第二次通过二相编码信号的匹配滤波器，得到最终的脉冲压缩信号。

1.2 信号特点

LFM信号和二相编码信号是广为采用的雷达脉冲压缩信号，但都有一定局限性。LFM信号存在较强的距离和多普勒频率交叉耦合，即当信号有一定的多普勒频移时，表现为脉冲压缩之后的主峰相对于没有频移所压缩后的主峰前移或是滞后； 二相编码信号对多普勒频率比较敏感，当有较大的多普勒频移时，与其匹配滤波器失配，信号不能被压缩。

通过对LFM-Chebyshev混沌二相码信号模型分析，其自相关函数是LFM信号和二相编码信号自相关函数共同作用的结果，既具有线性调频信号的宽带调频特性，又具有二相码信号良好自相关的特点，弥补了二进制相位编码信号的多普勒敏感特性。此外，由于Chebyshev混沌序列的随机性，信号互相关函数峰值低抗干扰能力强，并且具有较长的编码序列，得到的脉冲压缩信号压缩比更大。

2 干扰信号模型与分析

2.1 间隔采样转发干扰

间隔采样转发干扰是指干扰系统对截获的大时宽雷达脉冲信号高保真采样其中的一小段，进行处理并转发，采样与转发分时交替工作直到雷达脉冲信号结束。

如果间隔采样信号为一个方波脉冲串，脉冲宽度为，脉冲周期为，且/=1/2，间隔采样频率为=1/。则干扰信号经匹配滤波输出后的信号表达式为

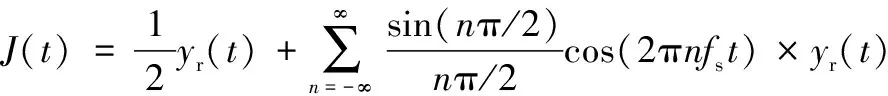
(7)

式中：()为真实目标回波信号通过匹配滤波器的输出响应,()=()⊗()。由式(7)可见，除了第一个假目标之外，其他假目标相对于目标回波有一个频谱搬移过程，频谱搬移的大小取决于=±。假设信号的带宽为，为了形成多个相干假目标干扰，那么有<； 又保证多个假目标都有逼真的假目标特性，那么假目标之间的时间间隔必定要大于回波压缩信号的主瓣宽度，即Δ>2。综上，产生多个相干假目标的条件为

1<<2

(8)

式中：为混合脉冲信号的时宽；为雷达信号的带宽。

2.2 卷积调制干扰

卷积调制干扰的基本思想是： 首先将接收到的雷达信号与一定带宽的噪声信号进行卷积，再将卷积之后的信号转发出去，从而形成干扰信号。这种干扰既有相参干扰的欺骗性，又具有噪声干扰的遮盖性。

卷积调制干扰的信号模型为

()=()⊗(-)

(9)

式中：()为一定带宽的噪声信号；(-)为干扰机接收到的雷达信号。设()为雷达信号的频谱，那么干扰信号经匹配滤波之后的时域输出为

()=()⊗[|()|]

(10)

式中：为傅里叶逆变换运算，[|()|]为点扩展函数，任意函数与点扩展函数进行卷积都能获得相应的脉冲压缩增益。由式(10)可见，噪声信号()也能获得脉冲压缩处理增益，从而提高干扰功率利用率。进一步，如果截取回波信号脉冲串进行噪声卷积调制，可产生多个高密度相参假目标，不仅具有噪声干扰特性，而且在时域和频域上可实现对目标的重叠和覆盖，提高对雷达的干扰效率。

2.3 移频干扰

移频干扰是利用LFM信号存在较强的距离和多普勒频率交叉耦合特性，在回波信号的基础上调制一个多普勒频移分量，就可以产生一个超前或者滞后于真实目标的假目标。根据移频方式的不同，可以有多种移频干扰特性。常见的移频方式有： 单点移频、 阶梯波移频、 线性函数移频、 分段线性函数移频。其干扰效果分别对应为： 产生单个假目标干扰、 多个假目标干扰、 单个覆盖干扰、 多个覆盖干扰。由于工程实用性，本文主要考虑阶梯波移频干扰和线性函数移频干扰。

阶梯波移频干扰的思想是把整个脉冲宽度分为段，每一段的长度为Δ=，起始频率为，移频的频率间隔为Δ，阶梯波移频干扰信号模型为

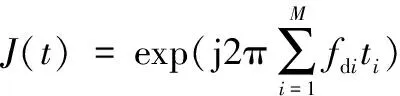
(11)

d=+Δ

(12)

∈[+(-1)Δ,+Δ]

(13)

由式(11)分析，对于每一段干扰信号而言，都是一个窄的失配的线性调频脉冲，经过匹配滤波后都能形成一个假目标，但是只有移频量d在[，](为信号带宽)范围内的信号才能通过匹配滤波器。

线性函数移频干扰是干扰机的调制频率按线性函数变化。如果在整个脉冲宽度内，干扰机调制的初始频率为，调制斜率为，那么干扰机本身的调制带宽为=。线性函数移频干扰的信号模型为

()=exp[j2π(+)]

(14)

由式(14)分析，由于干扰信号的线性调频特性，经过匹配滤波后输出不再是单个峰值，而是被展宽了，形成了覆盖性效果，展宽的宽度与干扰调制斜率相关。

2.4 距离干扰

距离多假目标干扰是一种有效的干扰方法，相对于传统噪声压制干扰方法，假目标信号与回波信号相参，能够获得雷达的信号处理增益，提高了干扰效率，而且工程上易于实现，使用灵活。当真实目标回波的延时与假目标的延时之差对应的距离大于雷达设计的距离分辨率Δ=2时，便可形成距离假目标欺骗干扰。由距离和时间的对应关系，只要对雷达回波做合理的延时就可以形成距离欺骗。因此，假设信号调频斜率为，Δ为对应延迟时间，距离欺骗干扰信号的模型为

()=exp[j2π(-Δ)]

(15)

距离多假目标干扰针对不同类型的雷达可以表现出不同的干扰效果，早期的研究主要集中于多假目标的欺骗干扰效果，而针对CFAR检测雷达，通过调整假目标复制的位置和数量，也能形成压制干扰效果。

2.5 距离-移频二维干扰

对于LFM信号，为了尽可能保持信号脉内调制特征，假目标干扰信号经匹配滤波后，可能超出距离波门，难以实现可靠的距离欺骗，可结合移频拖引的方法，达到距离欺骗的目的。而对于多普勒频率敏感的二相编码信号，难以实现移频干扰，但是二相编码信号距离分辨率较高，非常适合采用距离欺骗干扰，只需要回波附加一个小的延时，就能产生有效的距离假目标。

考虑到LFM-Chebyshev混沌二相码混合信号同时具有线性频率调制和相位编码的特征，这便构成距离-移频二维欺骗干扰对该混合信号有效干扰的理论基础。因此，假设信号调频斜率为，Δ为对应延迟时间，为移频频率，同时进行距离-移频二维欺骗干扰的子脉冲模型为

()=exp[j2π(-Δ)+j2π(-Δ)]

(16)

3 仿真分析

仿真参数设置为： 线性调频信号(LFM)带宽=50 MHz，时宽=1.2 μs，信号的采样频率=200 MHz，Chebyshev混沌信号码长=128，码元宽度=1.2 μs。根据以上参数设置，混合信号的带宽=50 MHz，脉宽==153.6 μs。图1为混合信号的波形(部分)和理想情况下的脉压输出时域波形。

图1 混合信号波形和脉压输出仿真结果

图2为采用间隔采样转发干扰在不同的间隔采样周期下的干扰效果图，干信比为6 dB。从图2可以看出，当间隔采样周期小于混合信号子脉冲宽度时，以主假目标为中心，能形成多个均匀分布、 幅度不等的假目标； 而当间隔采样周期大于混合信号子脉冲宽度时，只能形成一个主假目标。间隔采样周期越小，假目标数量越多，综合干扰效果越好，但所需功率也越大。可见，要形成多个假目标干扰，就需要对混合信号的子脉冲宽度进行较为准确的测量。

图3为采用卷积调制干扰的干扰效果图，调制噪声为0 dB，干信比为9 dB。从仿真结果可以发现，在真实目标周围存在多个距离不等、 幅度随机分布的假目标，并且各个假目标之间相互重叠，既具有欺骗干扰效果，又具有噪声压制干扰效果，功率利用率高。从卷积干扰的特性看，不需要精确测定信号的带宽和频率，通过接收回波信号与噪声卷积就能自动进行频率瞄准，是一种较为有效的干扰样式。

图4为采用移频干扰的干扰效果图。从图4可以看出，对混合信号的单个移频(移频量小于LFM信号带宽，干信比为6 dB)干扰能形成一个假目标，而线性函数移频干扰能形成覆盖式干扰。经过试验发现，只有在线性函数的斜率和混合信号中的LFM信号斜率相近时，干扰效果较理想。阶梯波移频干扰能形成多个假目标干扰效果，但总的干扰功率分散在各个假目标当中，当假目标数量较多时，干扰功率较分散，不能形成逼真的假目标干扰。因此，应根据混合信号中LFM信号的脉冲宽度，合理分配阶梯波的段数，即假目标的个数，才能达到较为理想的干扰效果。

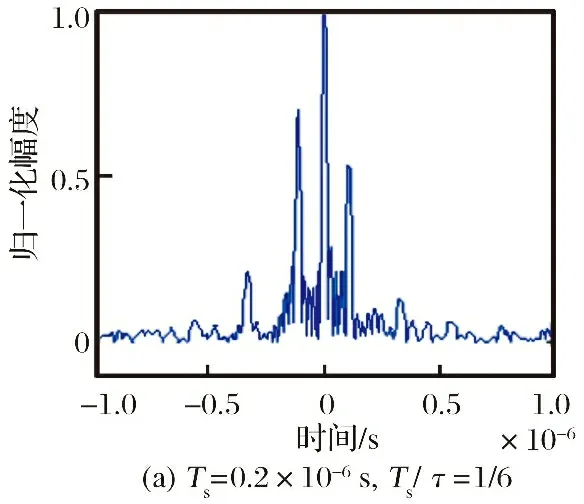
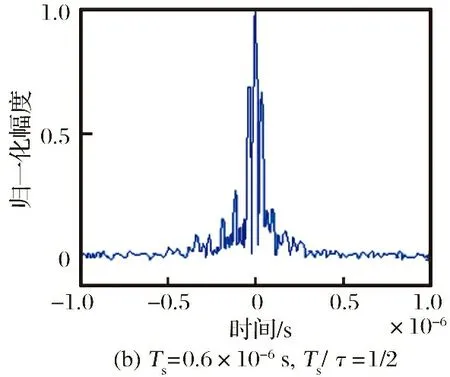
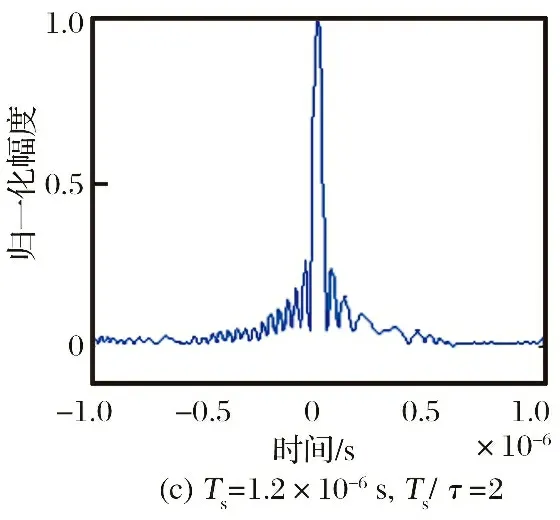
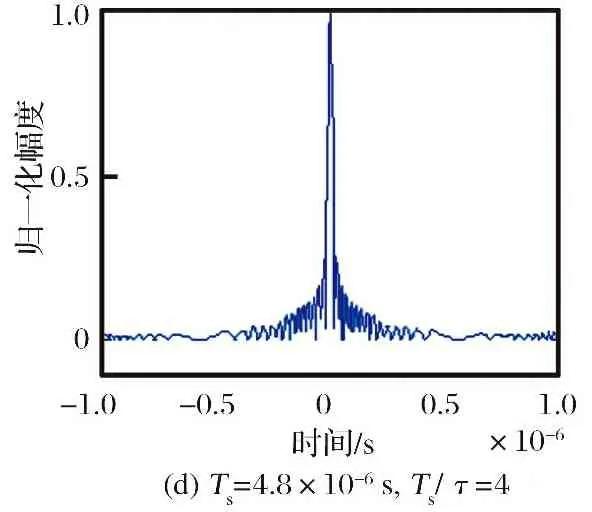
图2 间隔采样转发干扰仿真结果

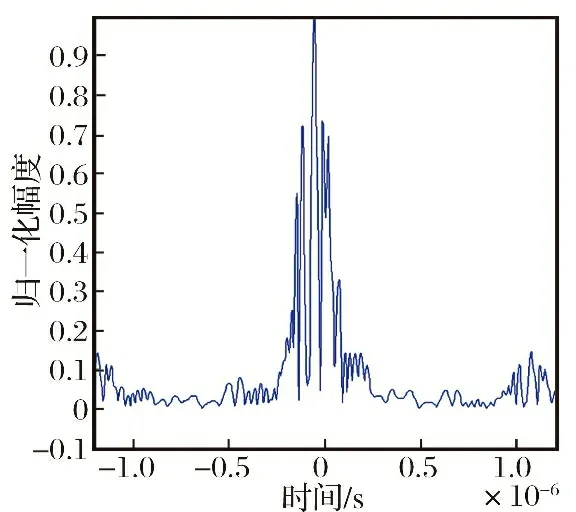
图3 卷积调制干扰仿真结果

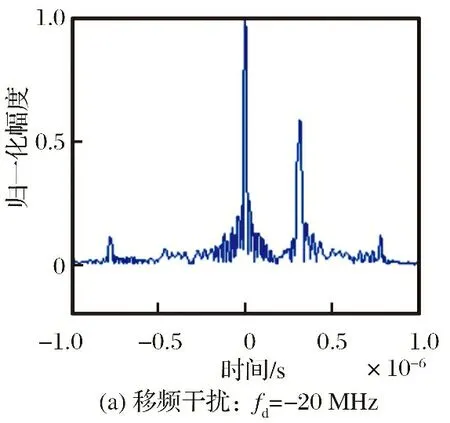
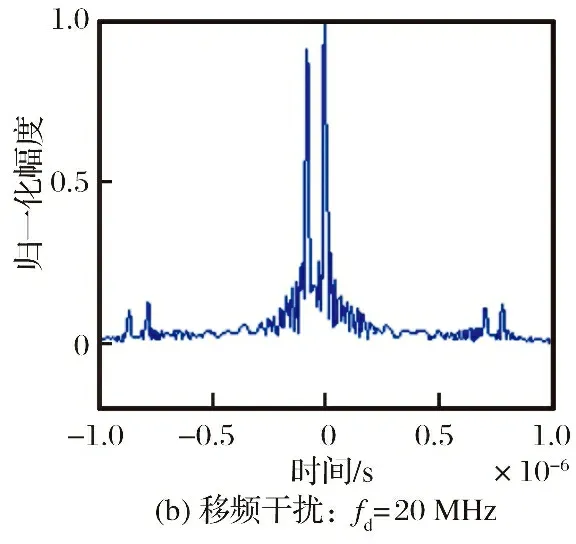
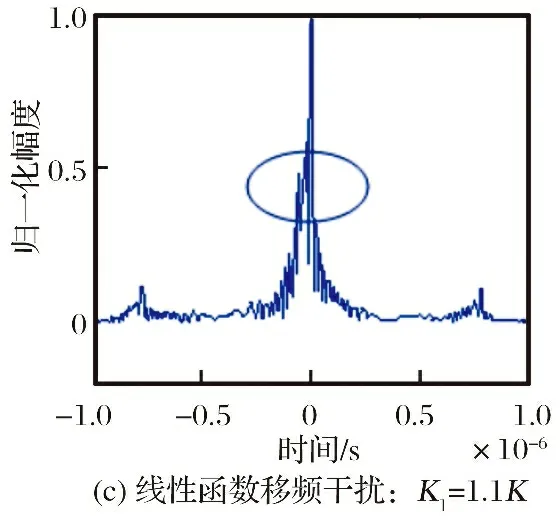
图4 移频干扰仿真结果

图5为采用距离干扰的干扰效果图。从图5可以看出，距离干扰也能对混合信号形成逼真的假目标干扰，干信比为6 dB。经过仿真发现，当子脉冲宽度是距离延时Δ大于1的整数倍时，能形成有效的假目标，其他情况则不能形成有效的假目标。如图5中所示，4个延时只有0.1 μs，0.6 μs两个延时形成了假目标，而1.2 μs，2.8 μs对应的延时则没有形成假目标，而且延迟越大，主瓣幅度值越低。因此，要对混合信号进行假目标距离干扰，需要对混合信号的子脉冲宽度进行较为准确的测量，以便控制延迟量。

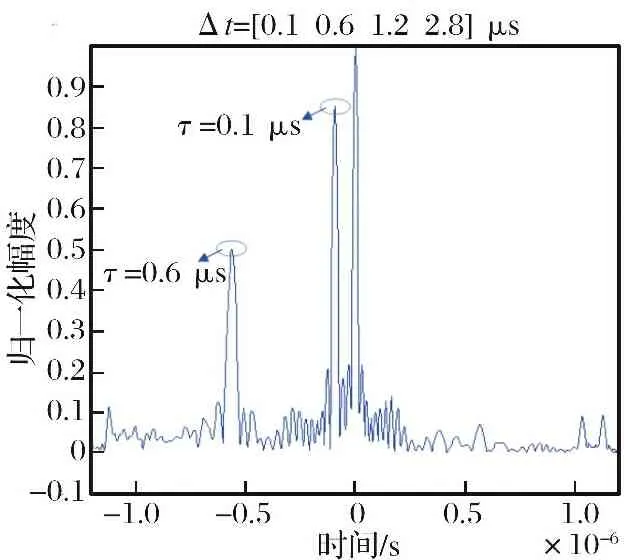
图5 距离干扰仿真结果

图6为采用距离-移频二维干扰的干扰效果图。从图6可以看出，距离-移频二维干扰对混合信号仍然有效，经过不同的多普勒频移和不同的时延，能够形成多个假目标干扰，干信比为12 dB。即使存在较大多普勒频移的情况下，干扰信号也具有脉冲压缩功能，其脉压输出类似于LFM信号的脉压结果。但是，随着移频量的增加，假目标主瓣幅度、 宽度和主副瓣比随之恶化，干扰效果较差。

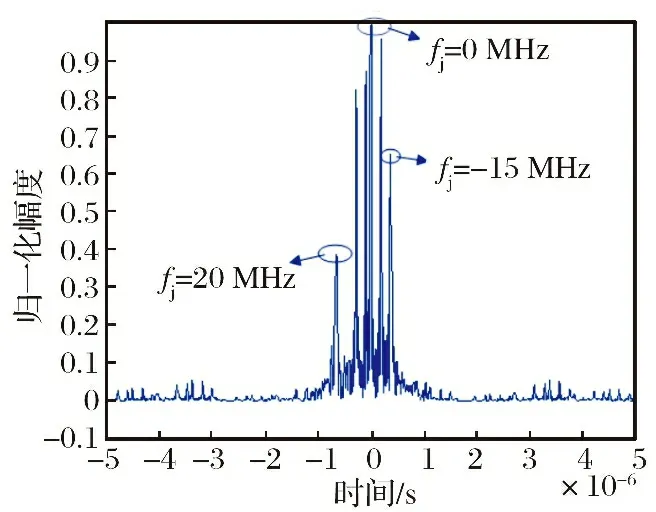
图6 距离-移频二维干扰仿真结果

综上仿真分析，可以得出以下结论：

(1) 由于LFM-Chebyshev混沌二相码混合信号具有LFM信号的特点，故任何对LFM信号有效的干扰方式，都能用于对LFM及其混合信号的干扰。

(2) 对LFM-Chebyshev混沌二相码混合信号的干扰，干扰参数的设置多依赖于子脉冲信号的特性参数，包括子脉冲LFM信号的脉冲宽度、 信号带宽、 以及调频斜率等。

(3) 上述五种干扰样式都能实现对LFM-Chebyshev混沌二相码混合信号实施干扰的目的，但是由于不需要专门的测频和频率引导，最易于实现的是卷积调制干扰。

4 结 束 语

面对复杂多变的环境和新型雷达信号，本文根据LFM-Chebyshev混沌二相码混合信号的特性，仿真验证了常用的五种典型干扰方式对LFM-Chebyshev混沌二相码信号干扰的有效性。分析表明： 对抗LFM-Chebyshev混沌二相码混合信号较为理想的干扰方式是卷积调制干扰，为电子战新型雷达信号干扰方式提供了思路。此外，仿真分析表明，LFM-Chebyshev混沌二相码信号子脉冲LFM信号的脉冲宽度、 信号带宽以及调频斜率等因素影响着干扰系统对雷达的干扰效果，这对电子侦察系统提出了较为苛刻的要求，也是实际应用亟待重点解决的问题。