热环境下复合材料壁板的非线性颤振特性分析
2022-10-11屈佑文安效民
屈佑文,安效民,邓 斌,闫 浩,周 悦
(西北工业大学 航天学院,西安 710072)
0 引 言
为了减轻结构重量,改善结构性能,各种新型复合材料被大量应用于高超声速飞行器结构中。飞行器高超声速飞行时,会出现气动加热,复合材料薄壁结构在气动载荷和热载荷作用下发生变形,导致流场的边界发生改变,使得作用在结构上的载荷发生变化,进一步影响薄壁结构的响应,使其产生新的变形或者振荡。这种结构、 气动和热之间的相互耦合作用,造成了壁板的热气动弹性响应问题。与传统翼、 舵等升力面构型不同的是,薄壁结构在非定常载荷作用下会表现出非线性流-固耦合特征: 其位移响应通常与厚度为相同量级,面内应力存在,弯曲和拉伸之间会发生耦合,在周围受约束条件下,形变一般不会引发结构的迅速破坏,表现为几何非线性。
国内外一些学者在该领域有一些很有意义的研究,Nydick等基于Marguerre薄壳理论和Galerkin方法求解结构变形方程,分析了高超声速气流中三维正交各向异性薄板的极限环幅值和振荡形态,指出壁板的气动弹性响应受到初始曲率、 气动热、 激波运动等的影响。Shiau等研究了高超声速气流中层合板的非线性颤振响应,指出材料各向异性对壁板的极限环和混沌运动形态等有显著影响。Gray结合Von-Karman板理论和三阶活塞理论分析了复合材料薄壁板的非线性气动弹性响应,分析了支承条件、 系统参数对颤振特性的影响。Kouchakzadeh等基于Galerkin方法计算了超声速气流中复合材料层合板的颤振特性,并讨论了面内应力、 纤维方向、 气动阻尼等对非线性响应的影响。
梁路等研究了具有复合材料壁板结构的机翼气动弹性问题,结果表明复合材料不同铺层的单层厚度比对机翼的刚度影响很大。欧阳小穂等研究了高速气流下变刚度复合材料壁板的非线性颤振响应,分析了支承条件和纤维方向等对颤振边界的影响。林华刚研究了非均匀温度场中复合材料圆柱壳的颤振特性,并进行了气动热-气动弹性耦合的计算分析。苑凯华等分析了复合材料壁板的非线性颤振特性,结果表明高超声速气流中气动力的非线性和热载荷对壁板颤振的振动幅值的影响更为明显。杨智春等利用有限元方法分析了不同铺层方向和铺层顺序对层合复合材料壁板颤振特性的影响,发现随温度升高,发生频率重合型颤振的耦合模态会发生演变,使得壁板有可能在较低的速压下发生颤振。
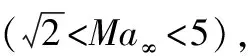
对于大尺度高超声速飞行器而言,在持续稳定飞行状态下,飞行器的表面存在近似均匀升温区域。本文基于均匀温度场针对复合材料薄壁结构在高超声速气流中的非线性气动弹性响应展开分析,建立了考虑热效应的复合材料壁板的非线性有限元求解模型,并将其应用于气动-结构的二阶松耦合方法中,用于分析考虑非线性非定常气动载荷和温度载荷共同作用下的非线性气动弹性问题,揭示非线性耦合的基本关系。
1 复合材料薄壁结构的非线性结构动力学建模
1.1 复合材料薄壁壳元的切线刚度矩阵
薄壁结构中面变形可以看作是薄膜变形和弯曲变形相互耦合的结果,引入一阶剪切变形假设。复合材料薄壁结构如图1所示,其中(,,)为单元参考坐标系,(,)为铺层材料参考坐标系。

图1 复合材料薄壁结构示意图
考虑热效应,单元参考坐标系下的单层应力-应变关系可写为

(1)

单元参考坐标系内,包括考虑热效应后的合力和力矩在内的所有合力和合力矩,都可以写成如下形式:

(2)

(3)
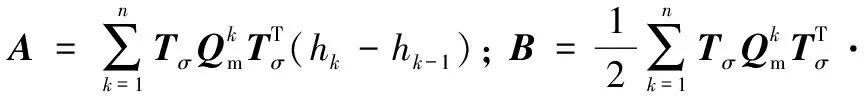
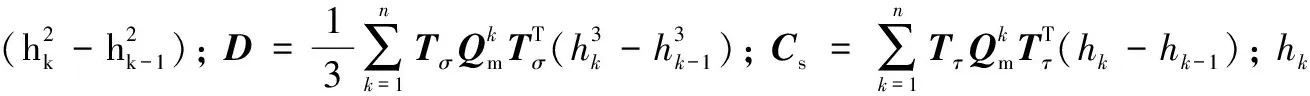
考虑单元参考坐标系和材料坐标系之间的转换关系,可知:
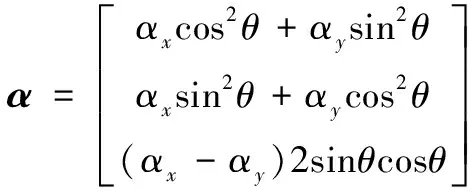
(4)
由此,可以推导得到单元参考坐标系中复合材料壁板壳元的刚度矩阵为

(5)
式中:,和分别为薄膜应变矩阵、 弯曲应变矩阵和横向剪切应变矩阵; 由虚功原理,热效应可以转换为温度载荷,其在单元参考坐标系中的表达式可以写为

(6)
利用高斯积分可以获得单元坐标下的刚度矩阵和温度载荷。考虑热效应后,载荷和单元位移的关系如下:
+Δ=
(7)
式中:和分别是单元参考系下的位移和载荷。
基于Co-rotational formulation (CR)理论,总体坐标系下的复合材料薄壁结构的切线刚度矩阵为
=+m
(8)
式中:m为几何刚度矩阵。
1.2 热效应下结构非线性动力学方程
基于哈密尔顿方程和虚功原理,不考虑结构阻尼的情况下,推导得到增量形式的结构动力学运动方程如下:

(9)

2 非定常气动载荷建模
无黏非定常流场的控制方程为Euler方程,其守恒积分形式如下:
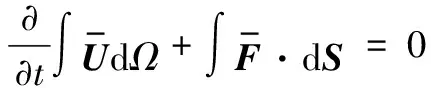
(10)


(11)

3 气动-结构二阶松耦合方法的计算流程
本文基于二阶松耦合方法(如图2所示),步骤如下:
(1) 利用时刻的结构信息,预测+12时刻的结构状态:
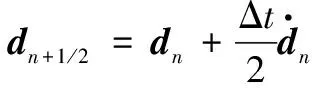
(12)
将耦合边界上的结构信息转换到流场网格中。为了在边界上满足应力连续,流场物面压强梯度考虑施加惯性力影响:

(13)

(2) 利用动网格算法更新流场网格,计算新的控制体体积。
(3) 求解式(11),获得+12时刻流场的压强,积分得到物面的气动载荷,将其转换为结构等效载荷s, +12,预估+1时刻的载荷:
s, +1=2s, +12-s,
(14)
(4) 利用Newmark方法求解式(9),得到+1时刻的结构状态。
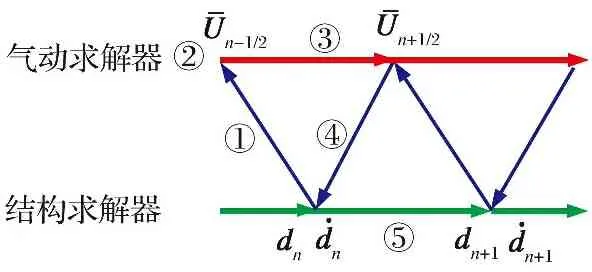
图2 流-固耦合示意图
4 算法验证
4.1 复合材料壁板的有限元建模验证
考虑一个四周固支的四层[/-/-/]复合材料层合板模型,如图3所示。材料属性为:=1,=1100,=500,=2 GPa,=154,=03,=08,=1 500 kg/m。

图3 复合材料层合板模型
考虑两种铺层结构:=45°, 90°。结构有限元网格数量为45×45,本文计算所得的前6阶自然频率如表1所示。本文的结果与文献中的结果相当吻合,说明了本文的复合材料有限元模型的可靠性。

表1 前6阶自然频率计算结果
4.2 热结构算例验证
以一个各向同性平板模型为例对热结构模型进行验证,其结构为:=1 m,=0.1 m,=1/100,=03,=2 700 kg/m,=10×10。弹性模量随温度的变化如图4所示。两端固支约束,有限元网格数量为41×5,初始温度为=100 ℃。
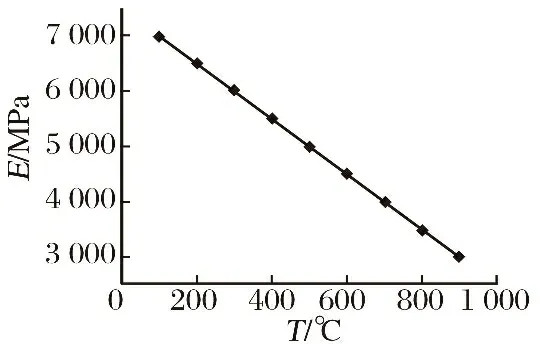
图4 弹性模量随温度的变化曲线
考虑温度场的变化[100 ℃,900 ℃],基于本文的热效应有限元模型进行模态分析,并与Nastran的结果进行比较。图5给出了在不同温度下前6阶热模态频率的计算结果对比。可以看出,本文的计算结果与Nastran的结果颇为接近,除了第4阶模态(该模态为扭转模态)有稍许差异外,其他模态的频率吻合较好。第4阶模态最大误差不超过9%,这种差异可能与两种算法的非线性刚度矩阵计算的不同有关。
由图可知,随温度的升高,各阶频率会随之降低,更高阶的频率下降幅度更大。这种特性很容易造成各阶模态运动之间的耦合,从而诱发如壁板颤振等不利的气动弹性现象。前两阶频率随温度出现了先降低后增高的趋势。以第1阶结构模态为例,其频率随温度的升高先变小,在400 ℃时达到最小,在超过429.5 ℃时,1阶频率又上升,此时结构发生了热屈曲,热屈曲以后会产生较大的变形。屈曲对板频率的影响,其原因较为复杂,与薄板屈曲构型、 温度梯度造成的热应力以及振动模态有关。本文计算中,基频模态在屈曲后频率随温度升高而增大。这也与Schneider等的研究结果相符。

图5 前6阶结构固有频率随温度的变化对比
4.3 非定常气动力计算验证
以AGARD CT5标模为例进行验证,翼型为NACA0012,马赫数为0.755,翼型非定常运动规律为()=0016+251·sin(2×0081 4) 。图6显示了本文计算的升力系数和俯仰力矩系数与实验值的比较。两者吻合很好,说明了本文所述方法应用于无黏非定常流场计算时的可靠性。
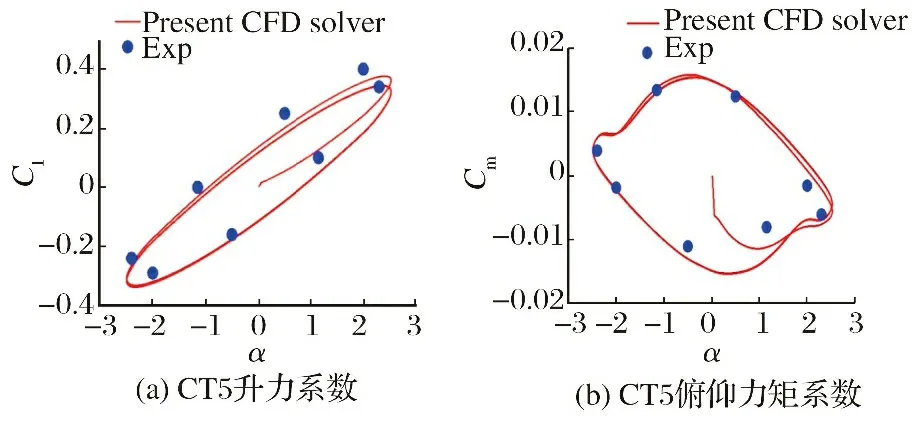
图6 AGARD CT5算例结果
4.4 三维壁板颤振分析验证
考虑一个三维各向同性壁板,如图7所示。其几何和材料特性为:=1,=0002,=03,=()=01,颤振分析时选取的计算状态为: 超声速=12, 壁板的流场网格为H型,包括121×121×39节点,结构有限元模型由1 152个三角壳元构成。

图7 三维壁板的几何构型
图8显示了壁板极限环振荡幅值和频率,并与Dowell和Gordnier的结果进行了对比。显然,与Gordnier的结果相符较好。Gordnier的求解器中同样采用了基于CFD的非定常载荷计算,而Dowell幅值稍高,因为其选用了线性势流理论来计算流场。这个算例也说明了本文耦合计算方法在处理气动力非线性和几何大变形结构非线性引起的气动弹性响应上的有效性。

图8 壁板极限环振荡幅值和频率随动压的变化
5 壁板的非线性热气动弹性响应分析
5.1 壁板模型与参数
壁板几何和材料属性参数为:==1.0 m,=0.005 m,=400,=06,=05,=025,=1 500,质量比=()=02。壁板四个边界均固支,壁板包含5个等厚度铺层。考虑两种铺层: 正交铺层板[0°90°0°90°0°](cross-ply)和斜交铺层板[45°-45°45°-45°45°](angle-ply)。计算工况为=5,给定温度条件分别为Δ=0 ℃, 50 ℃, 100 ℃, 200 ℃,分析壁板在不同动压下的非线性热气动弹性响应,以=075,=05作为参考点。
5.2 网格无关性和时间步长收敛性分析
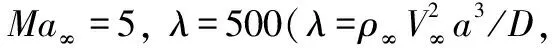
壁板流场网格为H型,考核了三种网格密度,沿壁板顺气流方向、 沿展向以及法向的网格点分别设置为: 81×81×29(壁板表面41×41)、 121×121×39(壁板表面61×61)和181×181×49(壁板表面81×81)。选取三个不同的无量纲时间步长: Δ=0015, 003, 006。采用Richardson外插方法考核网格和时间步长的影响,图9显示了以归一化无量纲振荡幅值为考核的收敛情况。

图9 不同网格和时间步长下的GCI收敛情况
综合考虑计算精度和效率,本文后续计算的网格选取为121×121×39,耦合计算时间步长Δ=003。图10显示了壁板流场网格,壁板在下表面中心位置,下表面设置为无穿透条件,流入边界上的变量由自由流超声速条件确定。在流出边界上,通过外推获得变量,其他边界变量由远场黎曼不变边界条件定义。图11显示了/=0.5剖面处壁板发生变形后的网格图。壁板流-固耦合响应计算中,不同下的流场初始值取的是刚性壁板的定常流场。

图10 壁板流场网格图

图11 y/b=0.5处壁板变形后的网格剖面
5.3 正交铺层壁板在不同温度下的响应分析
(1) Δ= 0 ℃下的响应分析
对于正交壁板,Δ=0 ℃时,发现=766时出现了颤振,其相平面图如图12(a)所示。随着动压的增大,后颤振的幅值和频率也会随之增加,在较大动压下,相图会出现粉刺现象,与高阶模态介入有关, 如图12(b)所示。图13~14分别显示了=1 500、 参考点振荡达到=0°(正向极值)和=180°(负向极值)时的壁板变形云图和流场压强云图。可以看出,此时的振荡形式表现除了结构的2阶模态之外,还有高阶形态参与其中。从压强云图来看,壁板参考点正向极值时前缘有激波,后缘为膨胀波; 其负向极值时前缘有膨胀波,后缘有激波出现。

图12 正交铺层在ΔT=0 ℃时不同动压时的相平面图

图13 正交铺层在ΔT=0 ℃下λ=1 500时壁板位移图
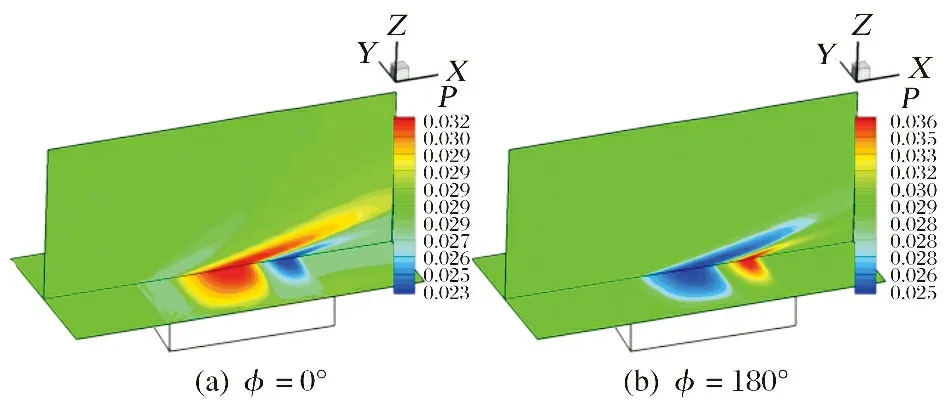
图14 正交铺层在ΔT=0 ℃下λ=1 500时压强云图
(2) Δ=50 ℃下的响应分析
当Δ=50 ℃时,在=377时出现了颤振,颤振动压相比未施加温度载荷的结果变小约50%,其相平面图如图15(a)所示。随动压增大,颤振幅值和频率也会随之增加, 如图15(b)所示。

图15 正交铺层在ΔT=50 ℃时不同动压下的相平面图
(3) Δ=100 ℃下的响应分析
当Δ=100 ℃时,壁板在亚临界下会出现静态屈曲。在不同动压条件下,该屈曲位置由正向朝负向发生了转变, 如图16所示。当动压增大到=120时出现了低频颤振,此时壁板无法保持在热屈曲的平衡位置,受到扰动后出现了振荡。 其响应相平面图如图17(a)所示,
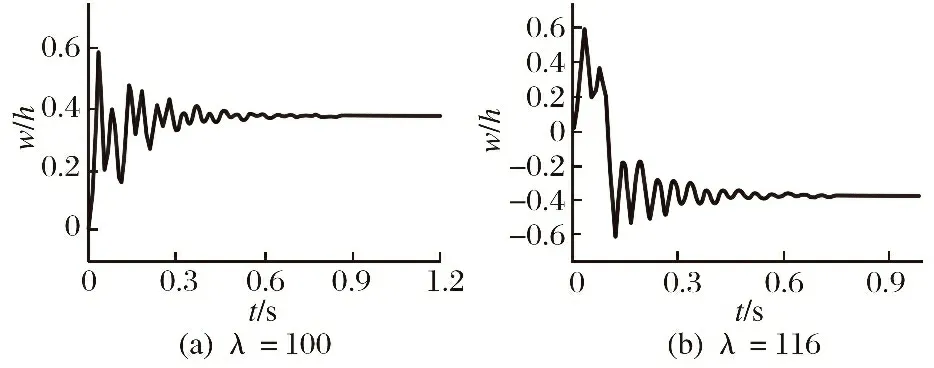
图16 正交铺层在ΔT=100 ℃时屈曲响应
出现了双环状构型。随动压增大,逐渐演化为单环形,如图17(b)所示。图18显示=1 000,=0°和=180°时的壁板变形云图。可以看出,此时的振荡形式表现为1阶自然振型。

图17 正交铺层在ΔT=100 ℃时各动压下的壁板相平面图

图18 正交铺层在ΔT=100 ℃下λ=1 000时壁板位移图
(4) Δ=200 ℃下的响应分析
当Δ=200 ℃时,其亚临界下的形态也表现为静态屈曲,不同动压下该屈曲位置也出现了正向到负向的转变,并且随着动压的增大,其收敛过程较长。其颤振出现在=249,从图19中可以看出,颤振及后颤振时壁板的形态表现为类似混沌运动。图20~21分别显示了=1 000,=0°和=180°时的壁板变形云图和流场压强云图。可以看出,此时的振荡形式中含有高阶自然振型,流场的压缩波和膨胀波分布与未施加温度载荷时相似。

图19 正交铺层在ΔT=200 ℃时不同动压下的相平面图

图20 正交铺层在ΔT=200 ℃下λ=1 000时壁板位移图

图21 正交铺层在ΔT=200 ℃下λ=1 000时压强云图
5.4 斜交铺层壁板在不同温度下的响应分析
(1) Δ=0 ℃下的响应分析
对于斜交铺层壁板,当Δ=0 ℃,=1 265时才会出现颤振,该临界动压远远超过了正交铺层壁板的值(约1.7倍),其响应如图22(a)所示,=1 500时的相平面图如图22(b)所示。图23显示了=1 500,=0°和=180°时的壁板变形云图。可以看出,此时的振荡形式主要表现为2阶自然振型,含有部分高阶形态。

图22 斜交铺层在ΔT=0 ℃时不同动压下的相平面图

图23 斜交铺层在ΔT=0 ℃下λ=1 500时壁板位移图
(2) Δ=50 ℃下的响应分析
当Δ=50 ℃,=689时出现了颤振。随动压增大,颤振幅值和频率也会增加,如图24所示。
(3) Δ=100 ℃下的响应分析
当Δ=100 ℃时,斜交壁板在未发生颤振时也出现了静态屈曲。随动压的变化,屈曲位置也会由正向朝负向转变。当动压增大到=284时出现了低频颤振,其响应相平面图出现了双环状构型,如图25(a)所示。随动压增大,这种构型逐渐演化为单环形, 如图25(b)所示。
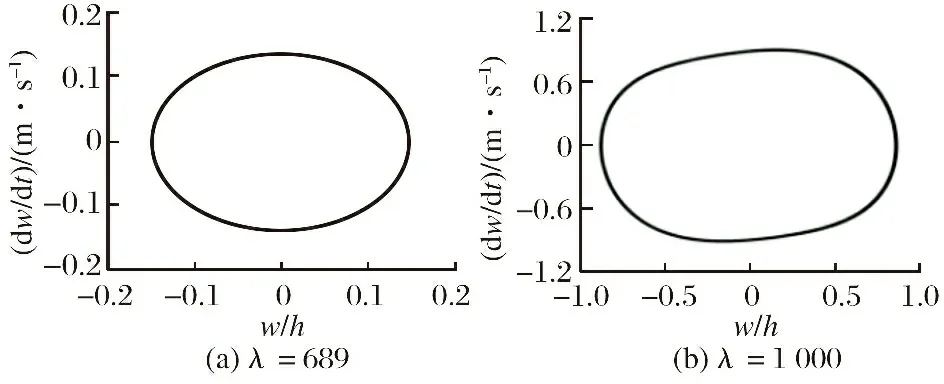
图24 斜交铺层在ΔT=50 ℃时各动压下的相平面图

图25 斜交铺层在ΔT=100 ℃时各动压下的相平面图
(4)Δ=200 ℃下的响应分析
当Δ=200 ℃时,亚临界下静态屈曲仍然存在,并且参考点屈曲位置也随着动压的变化而出现正向到负向的转换。颤振发生在=386,颤振及后颤振响应表现出拟周期特点,如图26所示。图27显示了=1 000,=0°和=180°时的壁板变形云图,可以看出,此时的振荡形式主要表现为1阶自然振型。

图26 斜交铺层在ΔT=200 ℃时各动压时的壁板响应相平面图
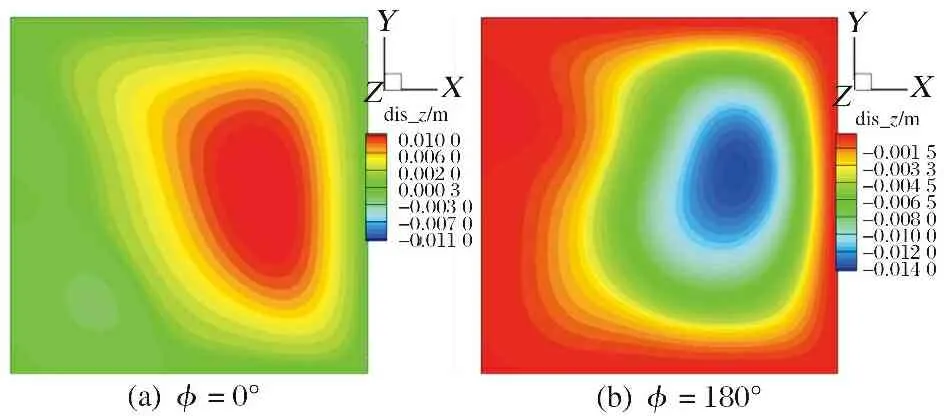
图27 斜交铺层在ΔT=200 ℃下λ=1 000时壁板位移图
5.5 不同温度载荷下复合材料壁板的响应对比
图28比较了两个壁板在不同温度下的振荡幅值与频率随动压的变化,可以看出,幅值和频率均随动压的增大而增大。Δ=0 ℃时,相同动压下,正交壁板的振荡幅值与频率均高于斜交壁板的值; Δ=50 ℃,=2 000时,正交壁板的幅值略小于斜交壁板的值(约91%); Δ=100 ℃时,两个壁板在小动压下呈现低频振荡(<10 Hz)、 振荡极值呈对称性; Δ=200 ℃时,斜交壁板在小动压时也表现为低频特征,且在较大动压(≥1 000)下,振荡极值呈现出非对称性。

图28 两种铺层壁板的振荡幅值和频率随动压的变化
图29显示了Δ=100 ℃和Δ=200 ℃时亚临界条件下参考点的屈曲位置。明显观察到两个屈曲平衡点,随着动压的增大,壁板的位置从正向平衡点向负向平衡点转换。相同动压条件下,斜交壁板的屈曲位移更大。
图30比较了正交铺层和斜交铺层在不同温度下的振荡幅值和频率随动压的变化。可以发现,极限环振荡的幅值随着温度的增加而增加,极值也呈对称特点。对于斜交壁板,在较大温度和动压条件下,会出现非对称的振荡。随着温度的增大,对于正交壁板,温度最大时,其振荡频率也最大,但斜交壁板对应最大温度载荷下的振荡频率最小。

图29 两种铺层壁板的屈曲位置随动压的变化


图30 两种铺层壁板的振荡幅值和频率随动压的变化
图31为正交铺层和斜交铺层在不同温度下的颤振临界动压和频率。可以发现,随着温度的增加,颤振临界动压先明显减小,Δ=100 ℃时,相比常温状态,两个壁板的减小量分别为84%和78%,而后随温度增加又增大; 相同温度下,斜交壁板的颤振临界动压高于正交壁板。对于颤振频率而言,正交壁板的颤振频率随温度载荷的增加,先减小后增大,而斜交壁板的颤振频率随温度载荷的增加而变小。

图31 两种铺层壁板在不同温度载荷下的颤振临界动压和频率
6 结 论
本文基于气动-结构二阶耦合的求解思路,针对非线性非定常气动载荷与非线性结构响应在热环境下的非线性气动弹性问题展开分析,建立了考虑热效应的几何非线性复合材料壁板求解模型,针对高超声速下不同铺层壁板的颤振特性对比研究,探讨了铺层方向、 温度等对颤振特性的影响。结论如下:
(1) 不同铺层的薄壁结构会呈现出不同的颤振特性。一般而言,斜交壁板的颤振动压高于正交壁板(增量大于55%),在相同动压下,正交壁板后颤振时的频率高于斜交壁板。在一定温度下,会出现低频颤振特性,与壁板屈曲有关。
(2) 随着温度的增大,颤振动压会下降,但出现热屈曲时,颤振动压又会缓慢增大。
(3) 当温度超过结构的临界屈曲温度时,壁板在亚临界条件下会出现静屈曲响应,而且存在多个屈曲平衡位置,该位置随着不同动压条件发生转变。
(4) 本文分析中温度为给定情况,流场求解考虑的Euler方程,后续研究中需要分析真实条件下气动-热-结构耦合下的响应情况。
(5) 本文仅针对高超声速典型马赫数状态点=5开展不同均匀温度场下的流-固耦合分析研究,所采用的方法对于其他高超声速马赫数状态下的研究具有参考意义,后续研究还需增加高超声速状态,以完整刻画其演变规律。
