FexRh1-x(0.4
2022-10-10廖从文卢志红袁晓娟冯金地李昆鹏
武汉科技大学学报 2022年6期廖从文,卢志红,袁晓娟,冯金地,李昆鹏
(1.武汉科技大学材料与冶金学院,湖北 武汉,430081;2. 武汉大学人工微结构教育部重点实验室,湖北 武汉,430072)
具有CsCl(B2)结构的等原子比FeRh合金在370 K 附近发生一阶反铁磁(AFM)到铁磁(FM)相变,伴随着约1%的晶格膨胀,其电阻率大幅降低,磁熵发生较大改变[1-5]。FeRh合金在AFM-FM相变过程中出现的磁性和电阻巨大改变以及略高于室温的相变温度等性质,使得其在热辅助磁记录(HAMR)介质的热磁开关等领域具有潜在的应用价值[6-7]。FeRh合金AFM-FM相变对各参数高度敏感,包括成分差异[8]、薄膜厚度[9]、磁场和应力[7,10]等。研究发现,可通过施加电场来调节由AFM→FM到FM→AFM的转变及由此产生的巨磁热效应[11-12],另外,有研究通过对混合相AFM-FM相变的调控得到大的电阻率变化[13]。这些效应主要归因于薄膜应变,而应变可通过施加电场来调制,可见FeRh薄膜AFM-FM相变与应变有较大关联[14]。大多外延生长的薄膜中均存在应变,并且其受到薄膜元素组成的影响,故研究FeRh薄膜与成分相关的磁序和相变动力学,通过调控成分来调节晶格应变及AFM-FM相变,对于FeRh薄膜在低功率自旋电子等领域的应用具有重要意义。
基于此,本文采用直流磁控测射技术制备了一系列不同成分比例的外延FexRh1-x薄膜(x表示Fe含量,原子百分比,范围为0.4~0.6),探究了x对FexRh1-x薄膜晶格畸变和磁性能的影响;此外,基于密度泛函理论(DFT)的第一性原理计算结果,分析了磁序及无序对FexRh1-x薄膜磁性能的影响。
1 实验与理论计算
利用直流磁控溅射技术,于873 K下将Fe靶和Rh靶共溅射至MgO(001)基片上,制备了不同成分比例的外延FexRh1-x薄膜。溅射系统基本压力保持在 7×10-5Pa 左右,实验气氛为Ar气,工作压力约为 0.5 Pa。利用Nano 400 Nova扫描电镜(SEM)及其配备的能谱仪(EDS)对所制薄膜成分进行分析,得到薄膜中x分别为0.42、0.49、0.52、0.53、0.58(原子百分比)。用D8 Advance型X射线衍射仪(XRD)对薄膜物相结构进行分析,利用同一设备的X射线反射(XRR)模块对薄膜表面质量和厚度进行表征,使用综合物性测量系统中振动样品磁强计(VSM)对样品的室温磁性及相变特性进行测试。
基于密度泛函理论(DFT)的第一性原理,采用 VASP 软件包进行模拟计算。借助全势线性缀加平面波(FP-LAPW)方法生成的广义梯度近似(GGA)方法,处理电子之间的交换关联能。通过收敛性测试后,平面波截断能设为500 eV,弛豫和静态计算均采用 Monkhorst-Pack方法产生的11×11×11网格精度进行布里渊区能量积分。在结构弛豫过程中,能量收敛标准为10-6eV,力收敛标准为0.1 eV/nm。对合金进行结构优化,达到收敛后再进行静态计算。为模拟实验情况下的FexRh1-x合金,特采用4×2×2超胞,图1为2×2×2超胞示意图,沿a轴扩充一倍即可得到4×2×2超胞。通过Fe原子取代Rh原子以及Rh原子取代Fe原子,计算了FexRh1-x合金在x=0.41,0.5,0.53,0.59时AFM相与FM相的能量差,确定FexRh1-x合金的磁基态。通过在2×2×2超胞中交换Fe原子与Rh原子位置,模拟Fe-Rh合金的无序状态,研究了FexRh1-x(x=0.5)合金的磁性随无序程度的变化。
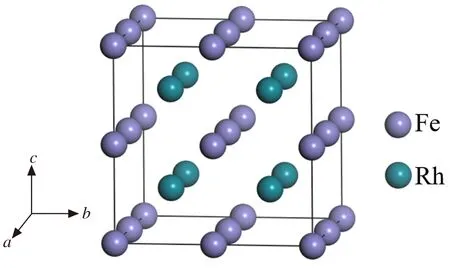
图1 FexRh1-x合金的超胞结构
2 结果与分析
图2为FexRh1-x(0.4为计算合金晶格应变εc,使用文献[1]报道的等原子比块状 FeRh 合金c轴的晶格常数0.2995 nm。表1列出了FexRh1-x(0.4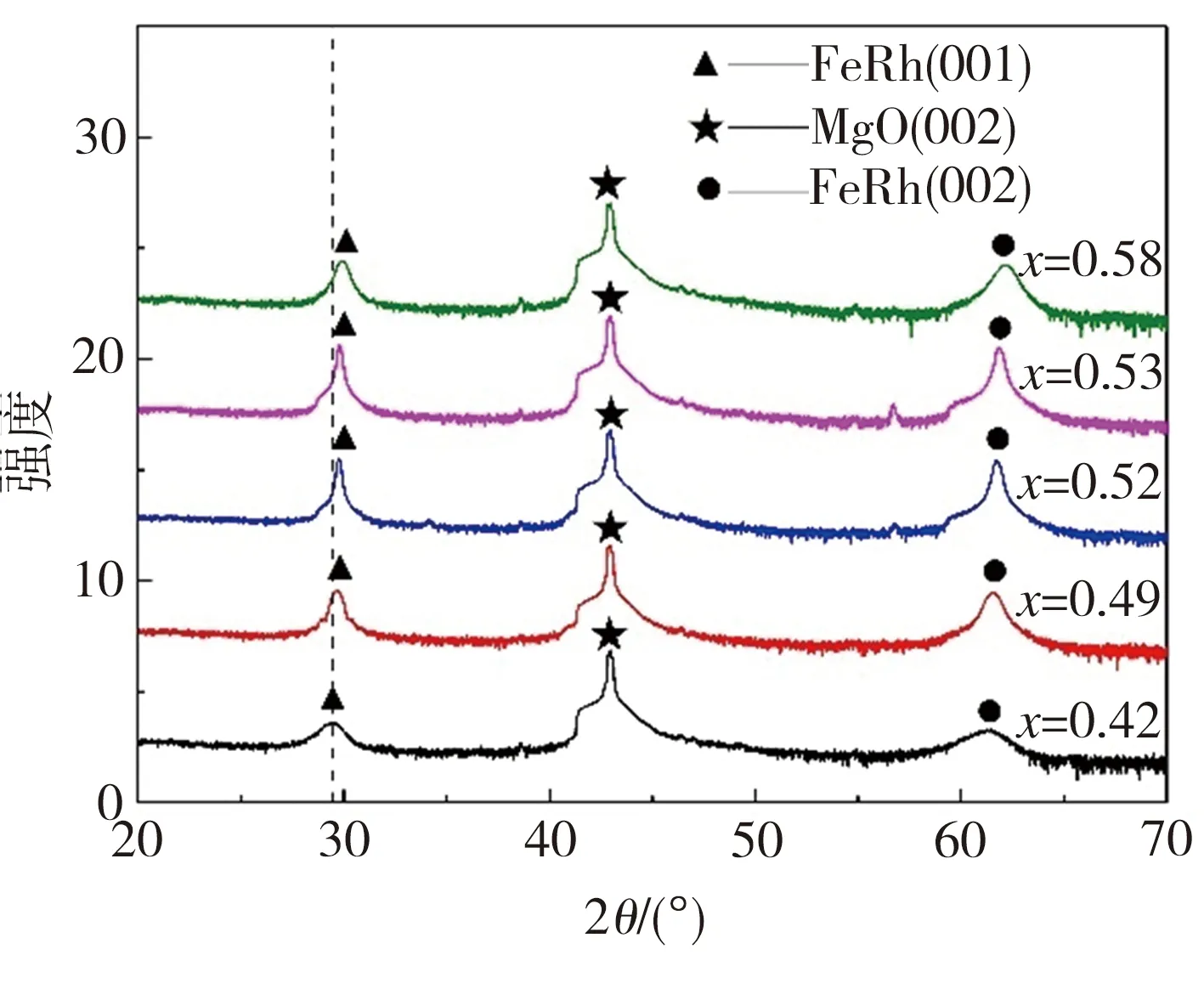
(a)XRD
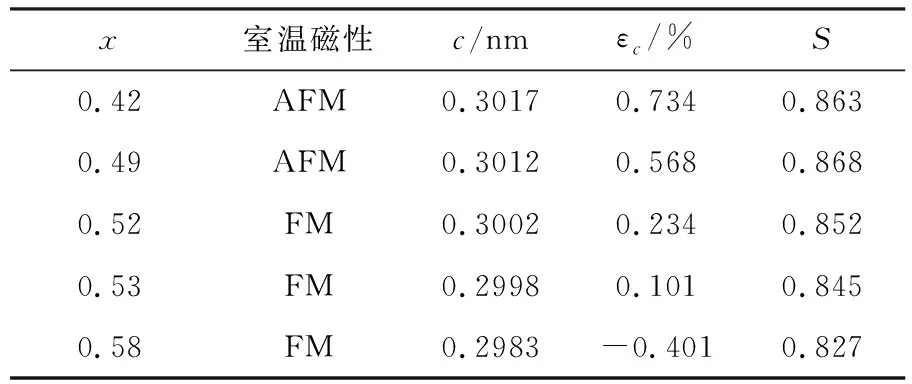
表1 FexRh1-x薄膜的结构参量
图3(a)和图3(b)分别为施加面内磁场和面外磁场时FexRh1-x薄膜的室温磁化曲线,可以看出,当x<0.5时,FexRh1-x薄膜在室温下磁性较弱,面外磁场下其磁化强度难以测量;x>0.5时,FexRh1-x薄膜在室温下磁性较强,整体表现为FM相,其中面内方向为易轴,在较低磁场强度下可达到磁饱和,x为0.52、0.53时,薄膜饱和磁化强度依次为1266、1402 emu/cm3,均低于理论值,可能是由其中部分无序成分所造成的,而面外方向为难轴,即使施加5000 Oe的磁场,薄膜仍难以达到磁饱和状态。表2列出了不同无序度下FeRh块体(等原子比)中Fe磁矩MFe、Rh磁矩MRh及单位晶胞总磁矩Mtot,由于使用的是2×2×2超胞,故每交换一对Fe-Rh原子,无序度增加12.5%。由表2可见,当无序度从0增加到37.5%时,MFe和MRh下降幅度较低,但Mtot随无序程度的增加而急剧下降,由此看来,磁矩实验值低于理论值可能是由于材料内部Fe和Rh原子的无序排列所引起的。
由图3(a)还可知,x<0.5时,薄膜饱和磁化强度仅为100 emu/cm3,表明其中主要成分为AFM相,含少量无序的FM相。通过第一性原理对FexRh1-x合金磁基态进行计算,通过在4×2×2超胞中使用Fe(Rh)原子取代Rh(Fe)原子来调节成分比例x,计算了x分别为0.41、0.50、0.53、0.59时FexRh1-x合金中AFM与FM相的能量差,结果如图3(c)所示,计算结果显示,当x>0.5时,FM相能量比AFM相能量低,表明富Fe合金的基态为FM相;当x≤0.5时,合金基态为AFM相。当合金中Fe原子较多(x>0.5)时,由于Fe原子会取代Rh原子的位置,此时Fe原子的最近邻原子由Rh变为Fe原子,使得最近邻Fe原子之间的交换作用破坏了次近邻Fe原子之间的反铁磁耦合,因此,合金磁基态由AFM相转变为FM相;而当Rh原子较多时,Rh原子会取代合金中Fe原子,由于Rh元素是顺磁性元素,故不会破坏Fe原子间的反铁磁耦合。
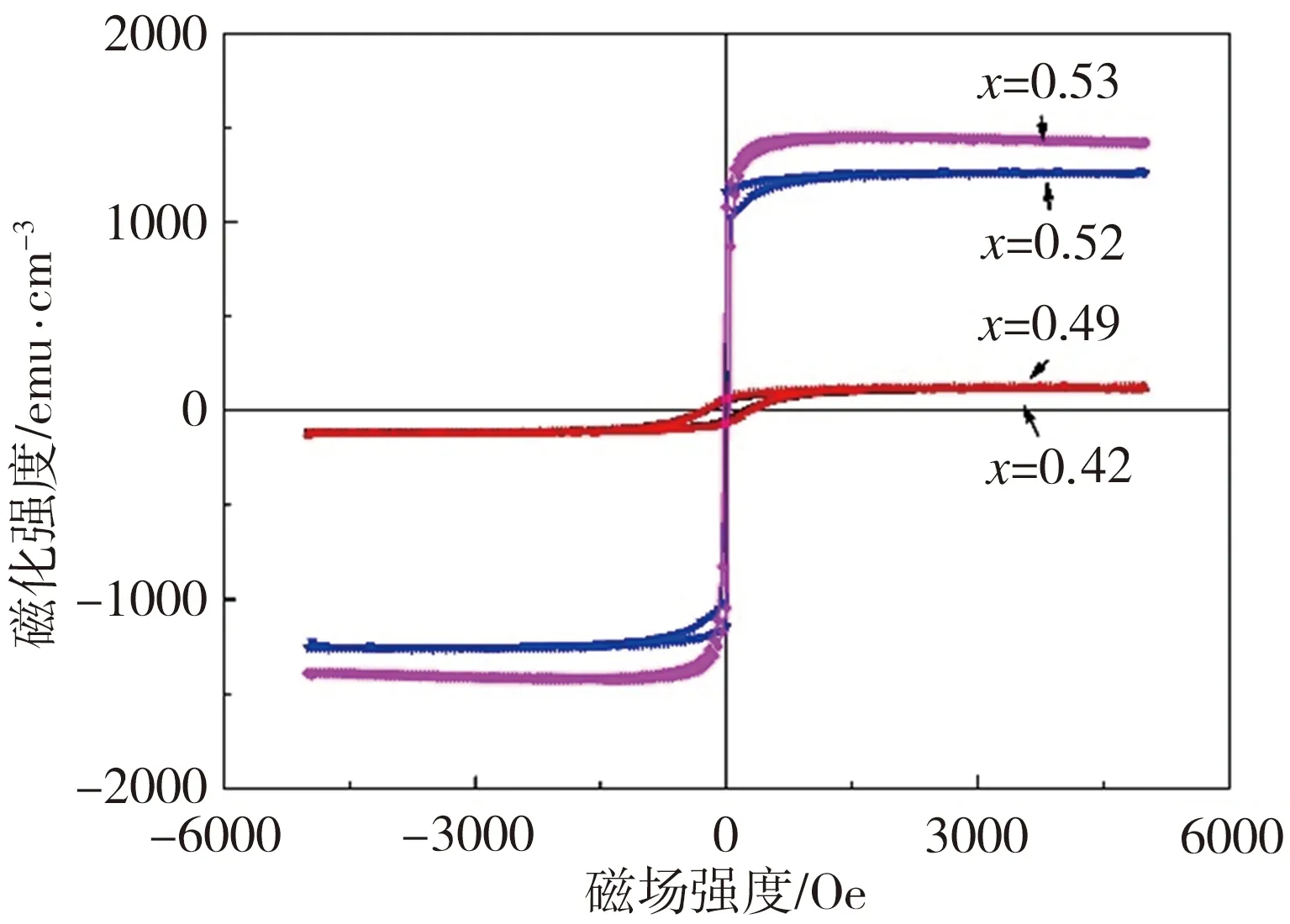
(a)面内磁场

表2 不同无序度下FeRh块体材料的磁矩
由于x>0.5时FexRh1-x薄膜无法发生AFM-FM相变,故选取能发生AFM-FM相变的FexRh1-x薄膜(x=0.42,0.49),测试其磁化强度随温度变化曲线,结果如图4所示。由图4可见,Fe0.49Rh0.51薄膜在340 K附近发生了AFM→FM相变;随着温度进一步降低,薄膜会发生FM→AFM相变,并出现热滞,升温时相变范围为340~400 K。对比Fe0.42Rh0.58样品的磁化曲线可知,随着Rh原子数增加,AFM→FM相变温度由340 K降至270 K,热滞温差由50 K降至30 K,相变范围由60 K增至120 K,表明过量Rh元素会促进FexRh1-x合金AFM→FM相变。Loving等[14]通过诱导界面应力,研究了相变温度与c/a的关系,XRD分析显示,当加入过量Rh元素时,由于Fe原子半径小于Rh原子半径,在内应力作用下,晶格膨胀,c轴产生应变,此时原子间距增加,反铁磁耦合作用减弱,故打破反铁磁耦合所需能量减少,其相变温度降低。根据上述规律,可通过调控薄膜中Rh原子比来改变薄膜c轴应变,从而得到需要的相变温度、热滞温差及相变范围。不过值得注意的是,尽管过量Fe元素也带来了应变改变,但这会导致FexRh1-x薄膜在整个温度范围保持铁磁性,故无法利用改变Fe含量的方式来调控相变温度。此外,相变温度降低还可能是受价带电子浓度(s+d电子/原子数量)的影响,当Rh取代Fe时,价带电子浓度增加,相变温度也会随之降低[15]。
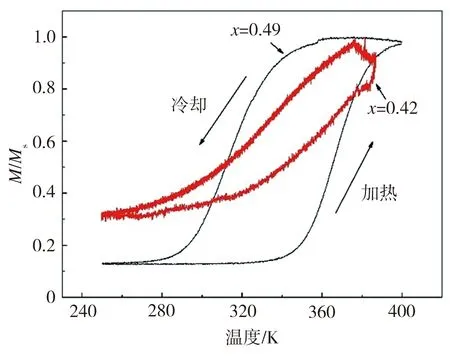
图4 FexRh1-x薄膜温度相关归一化磁化曲线
对Fe0.49Rh0.51薄膜样品进行磁热特性测量,从300 K加热至390 K,其中300~360 K时每隔20 K采集一次数据,360~390 K时每隔10 K采集一次数据,不同温度的等温磁化曲线见图5(a),经过式(1)处理后,得到3 T时,该样品磁熵随温度变化如图5(b)所示。
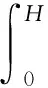
(1)
式中:ΔS为磁熵,J/(kg·K);T为温度,K;H为磁场强度,Oe;M为磁化强度,emu/cm3。
由图5(b)可见,在3 T的外加磁场作用下,Fe0.49Rh0.51样品磁熵随温度升高先增加后减小,在365 K时达到最大值,此时ΔSmax=14 J/(kg·K),略低于块体FeRh合金的磁熵值(ΔS≈16 J/(kg·K))[16],这可能是无序及二维尺寸下相变过程中铁磁相之间的相互作用所导致的。由此可见,FexRh1-x系薄膜(x=0.49)一阶相变的高磁熵在磁热领域具有较大的应用潜力,特别是在微型电子器件领域。
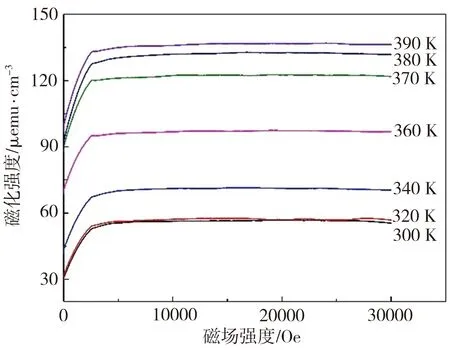
(a)等温磁化曲线
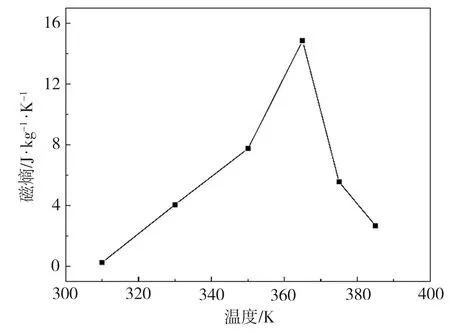
(b)磁熵曲线
3 结论
(1)随着x由0.42增至0.58,FexRh1-x薄膜(0.4(2)当x>0.5时,FexRh1-x薄膜在室温下为铁磁相,当x<0.5时,其在室温下为反铁磁相,这与基于第一性原理的理论计算结果相同,可能是由于Fe原子最近邻环境变化所致。富Fe的FexRh1-x薄膜室温下饱和磁化强度低于理论值,这可能因为所制样品中存在无序相,这一点通过理论计算也得到验证。
(3)随着Rh含量的增加(x由0.49减少至0.42),FexRh1-x薄膜的AFM→FM相变温度由350 K降至270 K,热滞由50 K降至30 K,相变温度范围由60 K增至120 K,这归因于Rh原子取代Fe原子所产生的内应变以及价带电子浓度增加。
(4)实验和模拟结果显示,可通过改变Rh含量及其带来的面外晶格中膨胀/收缩行为来研究 FexRh1-x薄膜的温度诱导相变行为,与温度相关的磁化测量结果与晶格参数变化非常吻合,并且该转变发生的温度范围和转变行为可通过改变薄膜中Rh含量来控制。
(5)在3 T的外加磁场作用下,FexRh1-x(x=0.49)薄膜的磁熵值最大可达到14 J/(kg·K),较大的一阶磁熵使得其在磁热领域有较强的应用潜力。
猜你喜欢
杂志排行
2022-10-10廖从文卢志红袁晓娟冯金地李昆鹏
廖从文,卢志红,袁晓娟,冯金地,李昆鹏
(1.武汉科技大学材料与冶金学院,湖北 武汉,430081;2. 武汉大学人工微结构教育部重点实验室,湖北 武汉,430072)
具有CsCl(B2)结构的等原子比FeRh合金在370 K 附近发生一阶反铁磁(AFM)到铁磁(FM)相变,伴随着约1%的晶格膨胀,其电阻率大幅降低,磁熵发生较大改变[1-5]。FeRh合金在AFM-FM相变过程中出现的磁性和电阻巨大改变以及略高于室温的相变温度等性质,使得其在热辅助磁记录(HAMR)介质的热磁开关等领域具有潜在的应用价值[6-7]。FeRh合金AFM-FM相变对各参数高度敏感,包括成分差异[8]、薄膜厚度[9]、磁场和应力[7,10]等。研究发现,可通过施加电场来调节由AFM→FM到FM→AFM的转变及由此产生的巨磁热效应[11-12],另外,有研究通过对混合相AFM-FM相变的调控得到大的电阻率变化[13]。这些效应主要归因于薄膜应变,而应变可通过施加电场来调制,可见FeRh薄膜AFM-FM相变与应变有较大关联[14]。大多外延生长的薄膜中均存在应变,并且其受到薄膜元素组成的影响,故研究FeRh薄膜与成分相关的磁序和相变动力学,通过调控成分来调节晶格应变及AFM-FM相变,对于FeRh薄膜在低功率自旋电子等领域的应用具有重要意义。
基于此,本文采用直流磁控测射技术制备了一系列不同成分比例的外延FexRh1-x薄膜(x表示Fe含量,原子百分比,范围为0.4~0.6),探究了x对FexRh1-x薄膜晶格畸变和磁性能的影响;此外,基于密度泛函理论(DFT)的第一性原理计算结果,分析了磁序及无序对FexRh1-x薄膜磁性能的影响。
1 实验与理论计算
利用直流磁控溅射技术,于873 K下将Fe靶和Rh靶共溅射至MgO(001)基片上,制备了不同成分比例的外延FexRh1-x薄膜。溅射系统基本压力保持在 7×10-5Pa 左右,实验气氛为Ar气,工作压力约为 0.5 Pa。利用Nano 400 Nova扫描电镜(SEM)及其配备的能谱仪(EDS)对所制薄膜成分进行分析,得到薄膜中x分别为0.42、0.49、0.52、0.53、0.58(原子百分比)。用D8 Advance型X射线衍射仪(XRD)对薄膜物相结构进行分析,利用同一设备的X射线反射(XRR)模块对薄膜表面质量和厚度进行表征,使用综合物性测量系统中振动样品磁强计(VSM)对样品的室温磁性及相变特性进行测试。
基于密度泛函理论(DFT)的第一性原理,采用 VASP 软件包进行模拟计算。借助全势线性缀加平面波(FP-LAPW)方法生成的广义梯度近似(GGA)方法,处理电子之间的交换关联能。通过收敛性测试后,平面波截断能设为500 eV,弛豫和静态计算均采用 Monkhorst-Pack方法产生的11×11×11网格精度进行布里渊区能量积分。在结构弛豫过程中,能量收敛标准为10-6eV,力收敛标准为0.1 eV/nm。对合金进行结构优化,达到收敛后再进行静态计算。为模拟实验情况下的FexRh1-x合金,特采用4×2×2超胞,图1为2×2×2超胞示意图,沿a轴扩充一倍即可得到4×2×2超胞。通过Fe原子取代Rh原子以及Rh原子取代Fe原子,计算了FexRh1-x合金在x=0.41,0.5,0.53,0.59时AFM相与FM相的能量差,确定FexRh1-x合金的磁基态。通过在2×2×2超胞中交换Fe原子与Rh原子位置,模拟Fe-Rh合金的无序状态,研究了FexRh1-x(x=0.5)合金的磁性随无序程度的变化。

图1 FexRh1-x合金的超胞结构
2 结果与分析
图2为FexRh1-x(0.4 为计算合金晶格应变εc,使用文献[1]报道的等原子比块状 FeRh 合金c轴的晶格常数0.2995 nm。表1列出了FexRh1-x(0.4 (a)XRD 表1 FexRh1-x薄膜的结构参量 图3(a)和图3(b)分别为施加面内磁场和面外磁场时FexRh1-x薄膜的室温磁化曲线,可以看出,当x<0.5时,FexRh1-x薄膜在室温下磁性较弱,面外磁场下其磁化强度难以测量;x>0.5时,FexRh1-x薄膜在室温下磁性较强,整体表现为FM相,其中面内方向为易轴,在较低磁场强度下可达到磁饱和,x为0.52、0.53时,薄膜饱和磁化强度依次为1266、1402 emu/cm3,均低于理论值,可能是由其中部分无序成分所造成的,而面外方向为难轴,即使施加5000 Oe的磁场,薄膜仍难以达到磁饱和状态。表2列出了不同无序度下FeRh块体(等原子比)中Fe磁矩MFe、Rh磁矩MRh及单位晶胞总磁矩Mtot,由于使用的是2×2×2超胞,故每交换一对Fe-Rh原子,无序度增加12.5%。由表2可见,当无序度从0增加到37.5%时,MFe和MRh下降幅度较低,但Mtot随无序程度的增加而急剧下降,由此看来,磁矩实验值低于理论值可能是由于材料内部Fe和Rh原子的无序排列所引起的。 由图3(a)还可知,x<0.5时,薄膜饱和磁化强度仅为100 emu/cm3,表明其中主要成分为AFM相,含少量无序的FM相。通过第一性原理对FexRh1-x合金磁基态进行计算,通过在4×2×2超胞中使用Fe(Rh)原子取代Rh(Fe)原子来调节成分比例x,计算了x分别为0.41、0.50、0.53、0.59时FexRh1-x合金中AFM与FM相的能量差,结果如图3(c)所示,计算结果显示,当x>0.5时,FM相能量比AFM相能量低,表明富Fe合金的基态为FM相;当x≤0.5时,合金基态为AFM相。当合金中Fe原子较多(x>0.5)时,由于Fe原子会取代Rh原子的位置,此时Fe原子的最近邻原子由Rh变为Fe原子,使得最近邻Fe原子之间的交换作用破坏了次近邻Fe原子之间的反铁磁耦合,因此,合金磁基态由AFM相转变为FM相;而当Rh原子较多时,Rh原子会取代合金中Fe原子,由于Rh元素是顺磁性元素,故不会破坏Fe原子间的反铁磁耦合。 (a)面内磁场 表2 不同无序度下FeRh块体材料的磁矩 由于x>0.5时FexRh1-x薄膜无法发生AFM-FM相变,故选取能发生AFM-FM相变的FexRh1-x薄膜(x=0.42,0.49),测试其磁化强度随温度变化曲线,结果如图4所示。由图4可见,Fe0.49Rh0.51薄膜在340 K附近发生了AFM→FM相变;随着温度进一步降低,薄膜会发生FM→AFM相变,并出现热滞,升温时相变范围为340~400 K。对比Fe0.42Rh0.58样品的磁化曲线可知,随着Rh原子数增加,AFM→FM相变温度由340 K降至270 K,热滞温差由50 K降至30 K,相变范围由60 K增至120 K,表明过量Rh元素会促进FexRh1-x合金AFM→FM相变。Loving等[14]通过诱导界面应力,研究了相变温度与c/a的关系,XRD分析显示,当加入过量Rh元素时,由于Fe原子半径小于Rh原子半径,在内应力作用下,晶格膨胀,c轴产生应变,此时原子间距增加,反铁磁耦合作用减弱,故打破反铁磁耦合所需能量减少,其相变温度降低。根据上述规律,可通过调控薄膜中Rh原子比来改变薄膜c轴应变,从而得到需要的相变温度、热滞温差及相变范围。不过值得注意的是,尽管过量Fe元素也带来了应变改变,但这会导致FexRh1-x薄膜在整个温度范围保持铁磁性,故无法利用改变Fe含量的方式来调控相变温度。此外,相变温度降低还可能是受价带电子浓度(s+d电子/原子数量)的影响,当Rh取代Fe时,价带电子浓度增加,相变温度也会随之降低[15]。 图4 FexRh1-x薄膜温度相关归一化磁化曲线 对Fe0.49Rh0.51薄膜样品进行磁热特性测量,从300 K加热至390 K,其中300~360 K时每隔20 K采集一次数据,360~390 K时每隔10 K采集一次数据,不同温度的等温磁化曲线见图5(a),经过式(1)处理后,得到3 T时,该样品磁熵随温度变化如图5(b)所示。 (1) 式中:ΔS为磁熵,J/(kg·K);T为温度,K;H为磁场强度,Oe;M为磁化强度,emu/cm3。 由图5(b)可见,在3 T的外加磁场作用下,Fe0.49Rh0.51样品磁熵随温度升高先增加后减小,在365 K时达到最大值,此时ΔSmax=14 J/(kg·K),略低于块体FeRh合金的磁熵值(ΔS≈16 J/(kg·K))[16],这可能是无序及二维尺寸下相变过程中铁磁相之间的相互作用所导致的。由此可见,FexRh1-x系薄膜(x=0.49)一阶相变的高磁熵在磁热领域具有较大的应用潜力,特别是在微型电子器件领域。 (a)等温磁化曲线 (b)磁熵曲线 (1)随着x由0.42增至0.58,FexRh1-x薄膜(0.4 (2)当x>0.5时,FexRh1-x薄膜在室温下为铁磁相,当x<0.5时,其在室温下为反铁磁相,这与基于第一性原理的理论计算结果相同,可能是由于Fe原子最近邻环境变化所致。富Fe的FexRh1-x薄膜室温下饱和磁化强度低于理论值,这可能因为所制样品中存在无序相,这一点通过理论计算也得到验证。 (3)随着Rh含量的增加(x由0.49减少至0.42),FexRh1-x薄膜的AFM→FM相变温度由350 K降至270 K,热滞由50 K降至30 K,相变温度范围由60 K增至120 K,这归因于Rh原子取代Fe原子所产生的内应变以及价带电子浓度增加。 (4)实验和模拟结果显示,可通过改变Rh含量及其带来的面外晶格中膨胀/收缩行为来研究 FexRh1-x薄膜的温度诱导相变行为,与温度相关的磁化测量结果与晶格参数变化非常吻合,并且该转变发生的温度范围和转变行为可通过改变薄膜中Rh含量来控制。 (5)在3 T的外加磁场作用下,FexRh1-x(x=0.49)薄膜的磁熵值最大可达到14 J/(kg·K),较大的一阶磁熵使得其在磁热领域有较强的应用潜力。




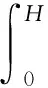


3 结论
