基于点云强度与高度信息的回环检测算法
2022-10-10胡雨欣颜俊杰张文俊
潘 锋,蒋 林,2,胡雨欣,颜俊杰,张文俊
(1.武汉科技大学冶金装备及其控制教育部重点实验室,湖北 武汉,430081;2.武汉科技大学机器人与智能系统研究院,湖北 武汉,430081;3.立得空间信息技术股份有限公司,湖北 武汉,430073)
回环检测算法用于判断机器人是否回到了曾经到过的位置,进而得到约束以消除机器人在即时定位与地图构建(simultaneous localization and mapping, SLAM)过程中产生的不可避免的累计误差[1-2]。根据所使用的传感器类型的不同,该算法可分为基于视觉的回环检测以及基于激光雷达的回环检测[3]。
基于视觉的回环检测算法通常利用词袋模型(BoW)[4],例如,Glvez-López等[5]采用FAST+BRIEF特征提取方法构建词袋,在多个数据集上进行实验,得到没有假阳性的回环检测结果;Cummins等[6]利用概率方法改进词袋模型并降低了计算复杂度;董蕊芳等[7]利用图像线特征提取二进制描述子进行视觉词典的构建,所得到的词袋中视觉单词评分间的区分度更高,从而提高了回环检测准确率,然而,该类方法容易受到环境如光照、天气和季节等变化的影响[8]。
激光雷达对环境中光照等条件的变化有较强的抗干扰能力,因此其在回环检测中得到更多的应用[9],常用的有基于局部描述符和基于全局描述符的回环检测算法。Rusu等[10]设置了一个16维的特征来描述点云的局部几何形状,通过特征计算对点云进行匹配以实现回环检测。Bosse等[11]构建了3D Gestalt局部描述符,采用关键点投票的方法构建分布模型来实现回环检测。Salti等[12]首先找到点云中的关键点,然后对关键点周围的点进行划分,将划分结果编码为直方图进行特征匹配。这几种经典的基于局部描述符的回环检测算法需要对点云中的特征进行详细描述,因此需要提取点云中的关键点和局部几何信息进行大量计算,算法准确率较高但运行效率较低,故而实时性较差。Muhammad等[13]、He等[14]则将三维点云投影到二维平面来生成点云的全局描述符,其方法虽然提高了回环匹配的计算速度但容易受噪声影响,不能保证较高的准确率。Kim等[15]提出了更加有效的全局描述符Scan Context,将点云的高度值编码为矩阵,保证了较快的计算速度,但在准确性方面仍有所欠缺,容易出现假阳性的情况。Wang等[16]随后提出了全局描述符ISC,利用强度信息将点云编码为二值化矩阵,虽然这能提高匹配速度,但二值化过程损失了部分点云信息,回环检测的准确率仍然较低。上述基于全局描述符的方法都仅仅使用单一的点云信息,检测准确率有待提高。另外,这些方法为了解决机器人在相同位置但不同朝向的情况下的回环检测问题(即旋转不变性问题),都要对与当前点云匹配的候选点云进行不断的旋转,重复计算相似度,使得计算量大为增加。
针对上述问题,本文提出一种同时利用点云几何信息和强度信息的回环检测算法。该算法使用两种方式分别将一帧点云的高度信息与强度信息编码为两个矩阵,构成能更加准确描述点云的全局描述符。同时,该算法利用SLAM前端得到的每一帧点云位姿,将点云的姿态变换到世界坐标系下,再对变换后的点云进行编码,这样可以解决旋转不变性问题,从而减少计算量。
1 基于点云强度与高度信息的全局描述符
通过激光雷达不仅可以得到周围环境的几何信息,同时还可以获取每一束激光返回的强度值。一般的回环检测算法仅仅利用点云中的几何信息,但点云的强度信息同样能体现其特征[17-18]。
本文算法中的全局描述符由两层构成,分别利用两种编码方式对点云的高度和强度信息进行编码。两种编码方式可以理解为从两个不同的视角来描述同一帧点云,这样得到的全局描述符能对一帧点云进行更全面和精确的表示,从而提高点云间的匹配精度,进而实现更高的回环检测精度。如图1(a)所示为一帧原始的三维点云,图1(b)为本文算法生成的全局描述符,由上下两层矩阵构成。

(a)原始三维激光点云
1.1 点云高度信息编码
全局描述符的第一层是将点云投影到二维平面进行编码得到对应的矩阵,其具体的编码方式如下:首先,由于雷达的测量精度随距离的增加会逐渐降低,所以要对输入的点云进行预处理,即定义一个距离阈值Dmax,选取与点云中心距离小于Dmax的点,得到新点云P,这样保留下来的点云数据更加可靠;然后,对点云P进一步划分,先根据半径将点云均匀地划分为若干扇形区域,扇形数量为Nc,然后用间距相等的同心圆将所有扇形划分为若干区域,设同心圆间距为Dr,则每个扇形被划分为Nr=Dmax/Dr个区域,划分结果如图2所示。
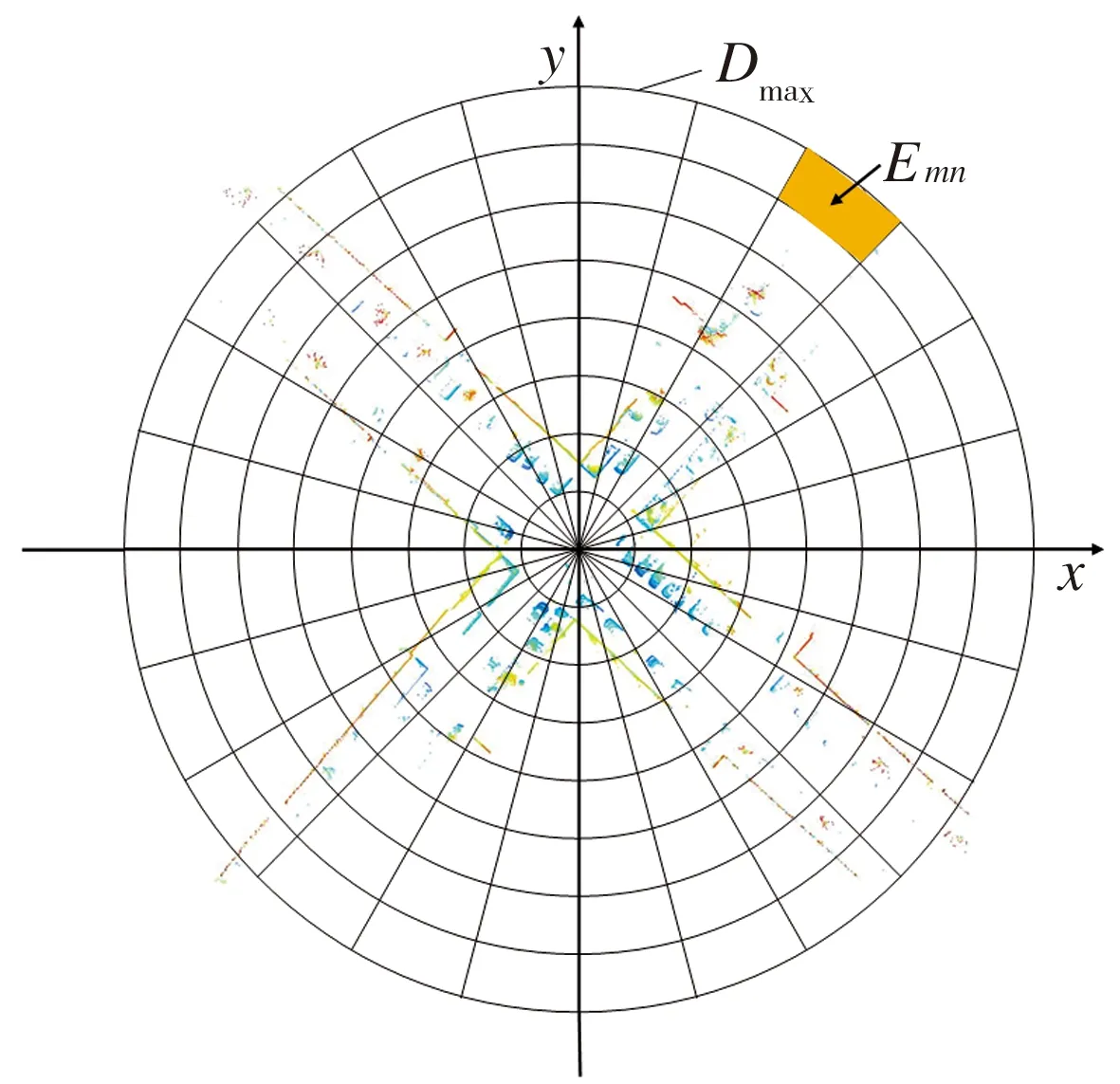
图2 点云的划分
点云一共被划分为Nr×Nc个区域,用Emn(m=1,2,…,Nr;n=1,2,…,Nc)来表示,Emn与大小为Nr×Nc的矩阵元素一一对应。若Emn区域内没有点,则对应矩阵元素取值为0,否则取每个区域中最高点的高度值为矩阵中对应元素的值,得到高度矩阵MH,用于表示一帧点云,其构成本文回环检测算法全局描述符的第一层。
1.2 点云强度信息编码
点云全局描述符的第二层利用点云强度信息构建,采用文献[19]中的编码方式。
将点云P中的点对应到大小为h×w的矩阵MI中。点云中每个点pn(x,y,z)和MI中元素的映射关系可以表示为:
(1)
式中:r为点到点云中心的距离;f为激光雷达垂直方向上的视角,例如三维激光雷达VLP-16的f=30°;v和u分别代表点所对应元素在矩阵中的行与列。
在点云中所有点对应到矩阵之后,将点的强度值赋予矩阵对应元素。例如,将KITTI数据集[20]中的一帧点云按上述方式映射得到的矩阵如图1(b)中第二层所示,因为采集KITTI数据集使用的是64线三维激光雷达,所以对应矩阵的行数和列数分别取h=64、w=900。
1.3 点云间相似度计算
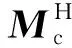
(2)
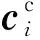
第二层矩阵之间的相似度S2可以通过相同方式计算得到。设置一个相似度的阈值τ,若S1+S2≥τ,则认为这两帧点云构成回环。
但是,如果机器人从不同的方向经过同一位置,此时得到的两层矩阵的列都会发生平移,如图3所示,其中两层矩阵的列发生平移的方向不一致是由不同的编码方式所导致。在这种情况下,直接计算矩阵之间的相似度并不能正确评价两帧点云的相似关系,即存在旋转不变性问题。为了解决这个问题,现有方法都是在计算相似度时让候选点云的矩阵保持不变,将当前点云矩阵所有的列向左平移一个单位,同时矩阵最左端的列移至矩阵最右端,从而得到一个新的矩阵,再重新计算新矩阵和候选点云矩阵之间的相似度,因此总共需要平移和计算的次数等于矩阵的列数,然后取其中最大的相似度作为最终结果。
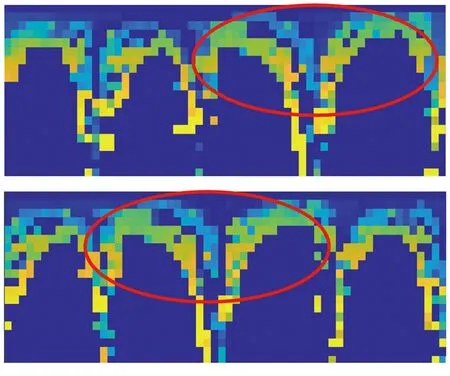
(a)第一层描述符
对矩阵的列平移相当于对点云进行旋转,如果两帧点云取自相同位置的不同方向,那么上述的最大相似度即为两帧点云旋转后对齐时的相似度,可以正确反映两帧点云的相似关系。但历史点云的数量会随机器人的运动不断累积,而激光雷达每得到新的一帧点云,就需要和所有的历史点云进行匹配,计算量会快速增加。因此本文算法在生成描述符之前,先利用SLAM过程中估计的当前帧点云姿态R对每帧点云进行一个旋转变换。如图4所示,当前点云经过变换后生成的描述符图4(b)和候选点云描述符图4 (c)的偏差较小,因此只需将当前点云矩阵进行左右平移,每平移一个单位计算一次相似度,且最多向左或向右平移3至5个单位,取其中最大相似度即可正确表示两帧点云之间的相似关系,这样可以明显减少相似度的计算。
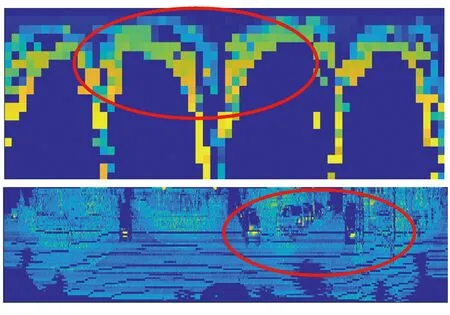
(a)当前点云全局描述符
2 回环检测算法
本文算法的整体流程如图5所示。首先通过旋转矩阵将当前帧点云姿态变换为世界坐标系下的姿态,再将点云编码为全局描述符,得到两个矩阵,进一步将矩阵简化为向量,利用KD树结构快速搜索2N帧可能发生回环的候选点云,再和当前点云进行精度更高的相似度计算,确定回环。
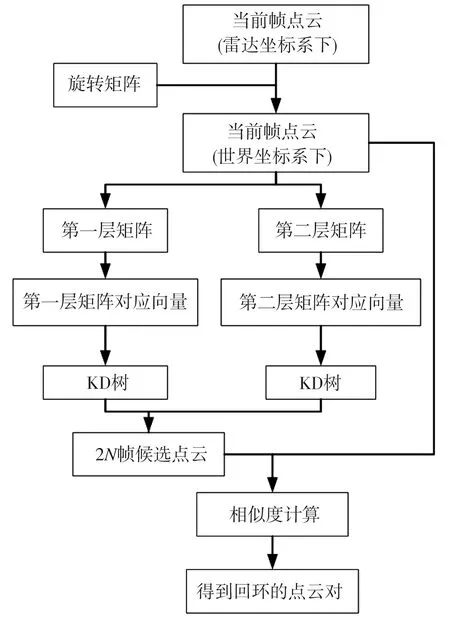
图5 本文回环检测算法流程
为了避免在所有历史点云中搜索与当前点云可能会发生回环的点云导致计算量随时间逐渐增大,进而影响算法的实时性,本文算法首先将全局描述符的矩阵转换为列向量,取矩阵每行所有元素的平均值作为列向量对应行的值。由全局描述符的两层矩阵M1、MH分别得到对应的列向量VI、VH:
(3)
(4)
所有历史点云都对应两个列向量,故可以通过两个KD树来保存所有历史点云的列向量,利用最邻近算法在KD树中进行高效搜索:①通过当前点云的两个列向量,分别在历史点云向量构成的两个KD树中找到与当前点云可能发生回环的N帧历史点云,这样一共能得到2N帧候选点云;②计算当前点云和所有候选点云的相似度,选出其中最大的相似度,通过阈值判断当前点云是否和历史某帧点云发生回环。通过这样的两步搜索策略,在保证计算速度的同时也能实现较高的匹配精度。
3 实验与结果分析
3.1 KITTI数据集实验测试
为了检测本文回环检测算法的性能,首先采用KITTI数据集的多个数据序列进行实验,在不同阈值τ下得到算法的多组准确率(precision)与召回率(recall)统计结果,绘制准确率-召回率曲线,并与文献[15]采用全局描述符Scan Context的算法进行对比,如图6所示。表1所示为两个算法在保证准确率为100%情况下的最大召回率。
从图6(a)、图6(b)可以看出,对于KITTI数据集的00、02序列来说,本文算法和文献[15]算法的结果接近,主要原因可能是由于数据集的场景所限,本文编码方式产生了退化,所以和Scan Context全局描述符相比优势不大。结合图6(c)、图6(d)和表1可见,本文算法在KITTI数据集的05、08序列上的表现明显优于对比算法,在保证回环检测准确率为100%的同时提高了召回率。这主要是因为本文算法利用两种编码方式对点云的两类信息进行编码,得到的全局描述符整体上能更加准确地描述点云,而且利用全局描述符的两个矩阵分别进行匹配,综合两个匹配结果实现互补,提高了回环检测的整体精度。
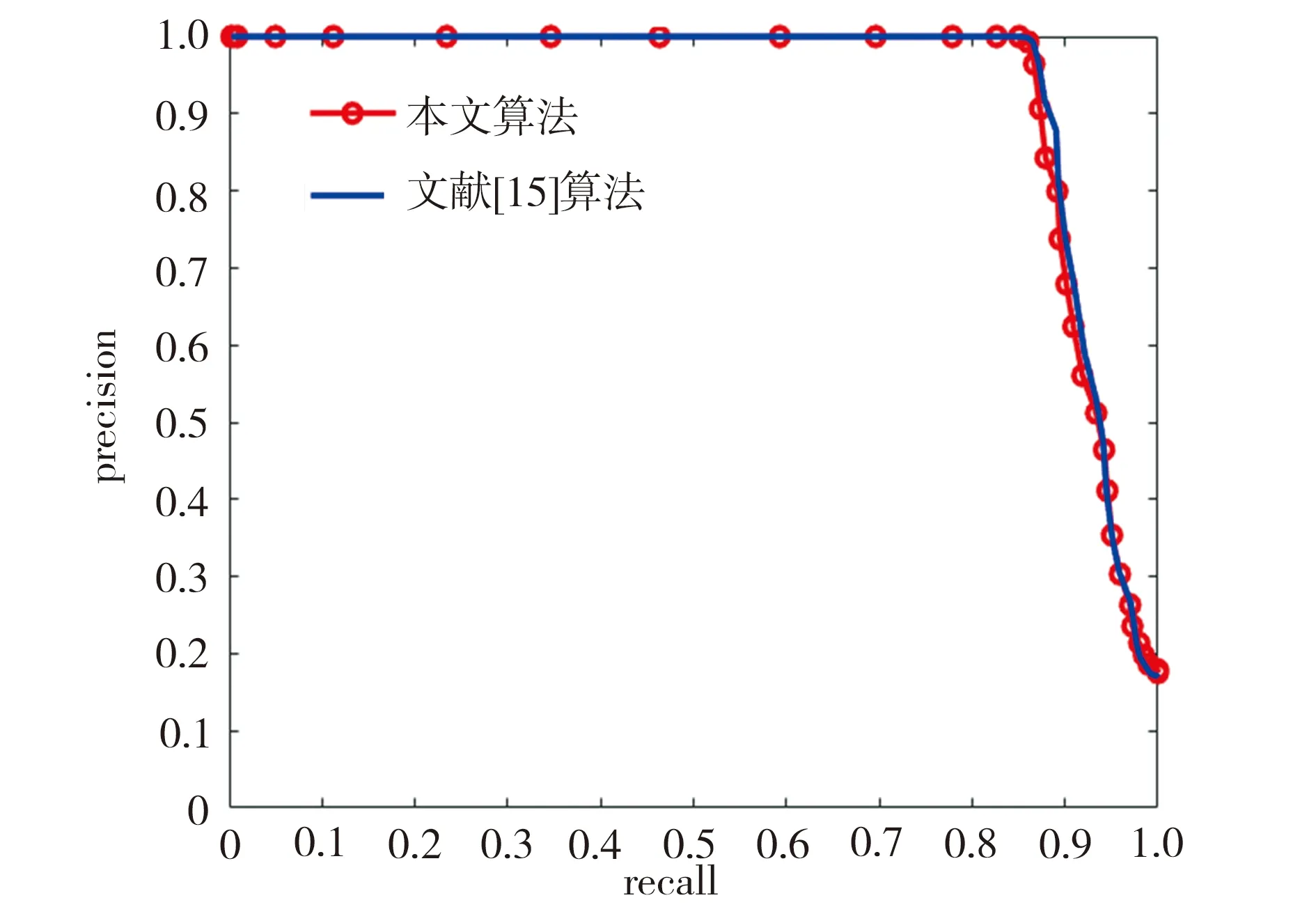
(a) KITTI 00序列
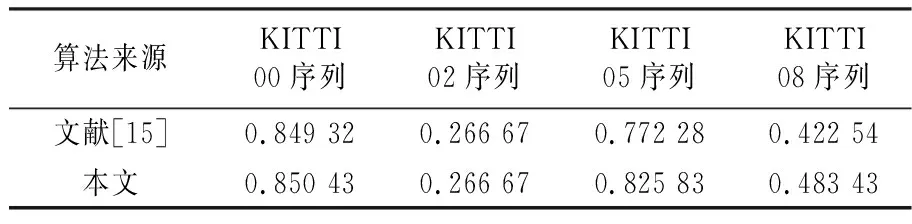
表1 两个算法在准确率为100%时的最大召回率
两个算法对每帧点云的计算时间如图7所示,平均计算时间见表2,可以看到,本文算法比文献[15]算法的计算效率提高了约40%。
(a) KITTI 00序列

表2 两个算法对点云的平均计算时间(单位:ms)
3.2 真实环境实验测试
下面在室外真实环境中运行本文回环检测算法。机器人实验平台如图8所示,机器人底盘上搭载VLP-16多线激光雷达、IMU和Intel NUC8 i7 HVK计算单元。在室外选择长约430 m、宽约120 m的矩形区域进行实验,图9为该区域整体点云地图,其中蓝线代表机器人的运动轨迹,而圆圈内是机器人发生回环的区域。

图8 室外移动机器人实验平台
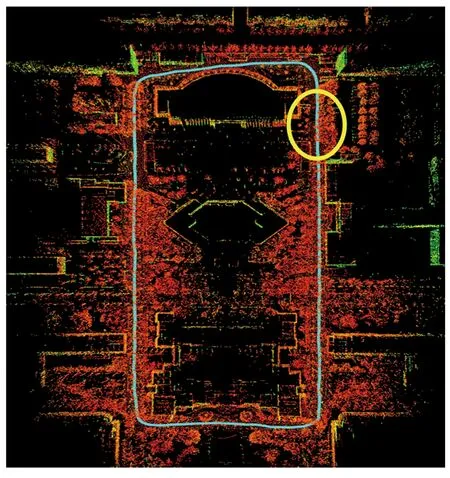
图9 室外实验环境的点云地图
首先,机器人在SLAM过程中使用常规基于距离的回环检测算法,在发生回环的区域内最终得到的点云地图和轨迹如图10所示。从图10(b)可以看出,机器人经过长距离地图构建后产生较大的累计误差,在Z轴方向出现较大偏移,无法成功进行回环检测,最终导致回环区域的点云不能正确匹配而产生重影,如图10(a)所示,两个黄色方框部分实为同一个区域。
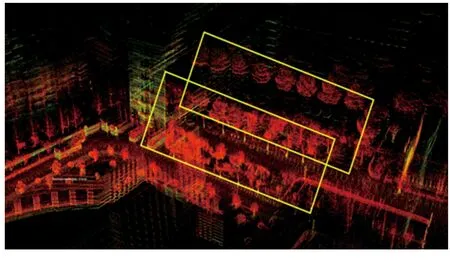
(a) 三维点云地图
将回环检测部分替换为本文算法后的实验结果如图11所示,可以看出,最终系统识别出机器人回到了原来的位置,正确地进行了回环,机器人的运动轨迹被修正,如图11(b)所示,相同区域的三维点云得到了准确匹配,如图11(a)所示。

(a)三维点云地图
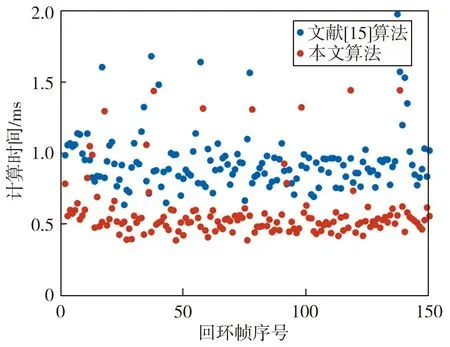
文献[15]算法和本文算法对真实环境中回环帧的计算时间如图12所示。本文算法在每个回环帧上的计算平均用时为1.015 ms,而对比算法的平均用时为1.780 ms,即本文算法的计算效率提高了约43%。

图12 室外实验中两个算法的计算时间对比
4 结语
针对现有基于激光雷达并采用全局描述符的回环检测存在的不足,本文提出了一种同时利用点云几何信息和强度信息的回环检测算法,其首先利用机器人在SLAM过程中得到的旋转矩阵对点云进行姿态变换,再通过两种不同的编码方式对同一帧点云的高度与强度信息进行编码来构建点云的全局描述符,最后通过两步匹配策略搜索出发生回环的点云。与采用Scan Context全局描述符的同类型算法比较,本算法在公开数据集KITTI上的实验中整体表现出更高的回环检测精度和更快的运行速度。在真实室外环境中运行了集成本文回环检测算法的SLAM算法,其建图效果也有明显改善。
