路基边坡逐孔微差爆破对邻近桥梁的影响❋

2022-10-10罗如登鲍志斌王正阳

爆破器材 2022年5期

罗如登鲍志斌王正阳

①中南大学土木工程学院(湖南长沙，410000)

②中交二航局建筑科技有限公司(湖北武汉，430000)

引言

工程爆破广泛应用于山区土木工程基础开挖项目中，为推动我国基础设施建设发挥了非常重要的作用。在钻爆法施工过程中，爆破安全一直是工程爆破行业关注的重要问题。采用钻爆法开挖时，经常会面临对爆破点邻近目标(如既有桥梁)的保护。控制爆破地震波对邻近桥梁结构安全性的影响，同时又确保在建项目的高效爆破施工，是爆破施工单位、行政主管部门、监理单位等多方共同面临的技术难题[1-7]。

丁茂瑞[8]利用二维数值分析研究了新建隧道爆破开挖对邻近既有桥梁的安全性动力影响。黄赫烜等[9]通过监测数据，研究了隧道爆破和钻孔灌注桩施工对邻近高铁桥梁的影响，并结合有限元模型分析了桥梁的安全性和可靠性。孟灵鑫等[10]基于FLAC3D用瞬态动力学方法，分析了爆破振动对邻近桥面及桥墩的影响。李杰[11]在水下爆破中，对邻近桥梁振动危害进行了实时监测及数据分析。

近年来，随着高精度雷管、数码电子雷管等新型爆破器材的问世，通过微差爆破技术可改善爆破效率、提高爆破质量，同时可有效减少爆破地震波、冲击波等的危害效应[1-3，12]。

贵黄高速公路TJ13 标段路基边坡，爆区之间有一既有高铁桥梁需要保护。为确保爆破安全，需结合邻近保护目标的振动危害效应监测信号及数值模拟分析，开展微差爆破方案优化研究。

1 现场试验设计

贵黄高速公路TJ13 标段路基边坡长260 m，爆区宽20 m，开挖高度16～20 m，中硬岩，总石方量约20 000 m3。爆区I和爆区II之间的既有高铁桥梁需被重点保护。其中，七号墩距爆区最近，离爆区I北面340 m，爆区II南面582 m，如图1 所示。

试验方案设计如下:

1) 爆区I距离既有桥梁更近。现场试验时，采用TC-4850 爆破测振仪，在爆区I微差爆破时对邻近高铁桥梁的振动响应进行实时数据采集。

2) 将爆区I的边坡开挖成高1.5 m、宽1.5 m的台阶，在边坡中部钻3 个炮孔，孔径100 mm、孔深3.0 m、孔距3.0 m，单耗取0.35 kg/m3，逐孔起爆，孔间微差时间初步设定为6 ms。

3) 测点布置在七号墩以及离爆源中心直线距离最短的第六跨梁，测点编号如图2 所示。迎爆侧，从七号墩底开始间隔2 m 布置1＃～5＃测点，从第六跨梁跨中梁体开始间隔2 m 布置6＃～10＃测点，桥墩上1＃测点、梁体上7＃测点距爆源最近。

2 数值模型建立

2.1 计算模型

基于ANSYS/ LS-DYNA软件，建立爆区I边坡和邻近既有桥梁的1∶1 数值计算模型。采用ALE算法，Solid164 单元，长340 m，宽260 m，按实际尺寸建立3 个炮孔，微差起爆时间6 ms，总计算时长200 ms。桥梁结构建模时进行简化，跨径30 m，梁和墩模型材料分别为C55 和C50 混凝土。总体建模如图3 所示。

2.2 材料模型及参数

岩石采用弹塑性动力模型(Mat_Plastic_Kinematic)。该模型能精确地模拟岩石材料的动力特性，其屈服条件为[13]:

式中:sij为柯西应力张量；aij为屈服面中心点处的应力偏张量；F和C为输入常数；σy为屈服应力；σ0和β分别为初始屈服应力和硬化参数；为应变率；Ef为塑性硬化模量，Ef=EtE/(E -Et)；E为弹性模量；Et为切线模量；为有效塑性应变。

根据地质资料，岩石力学参数如表1 所示。

表1 岩石参数Tab.1 Parameters of rock

梁和墩分别采用标号为C55 和C50 的混凝土，混凝土材料参数见表2。

表2 混凝土参数Tab.2 Parameters of concrete

炸药采用高能炸药材料模型(Mat_High_Explosive_Burn)，结合JWL 状态方程[13]，对炸药起爆点、起爆时间加以控制，实现对炸药爆炸过程的模拟。

式中:p为爆轰压力；V是相对体积；E是单位体积内能；ω、A、B、R1、R2为材料常数。

具体参数如表3 所示。

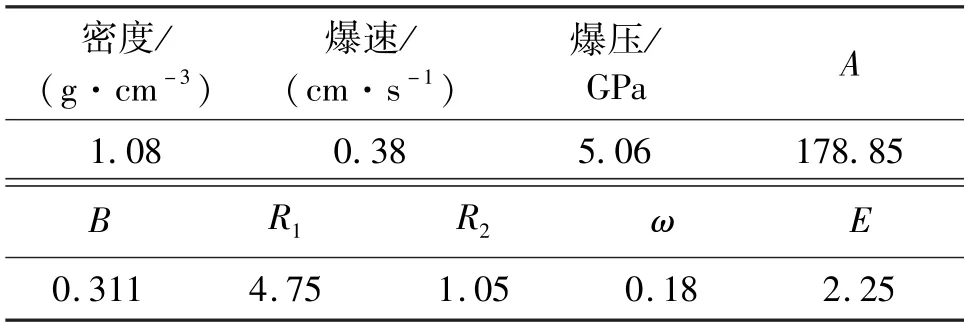
表3 炸药材料及状态方程参数Tab.3 Parameters of explosive material and equation of state

2.3 边界条件

在有限元模型中，需要采用有限域来模拟爆破地震波作用下炸药爆炸产生的邻近高架桥的动力响应规律。在ANSYS 建模过程中，需要在范围有限的模型边界上施加无反射边界条件，消除爆破地震波传递到模型边界时发生的反射、折射现象，确保计算结果的准确性。在计算模型中，除上部边界面外，其余模型面均施加无反射边界。

2.4 数值计算方案验证

基于上述试验和数值模拟方案，将逐孔起爆微差时间6 ms 时，实际采集到的桥墩和跨梁上各测点的爆破振速峰值与数值模拟计算所得各测点的振速峰值进行对比，如图4 所示。总体吻合情况良好，最大偏差不超过10%，验证了上述所采用的数值模拟方案基本科学合理。

3 数值模拟分析

采用控制变量法进行数值模拟及对比分析。保持测点位置不变，研究微差时间对邻近桥梁同一测点处振速响应的影响规律；保持微差时间不变，研究测点所处空间位置对测点处振速响应的影响规律。

在上述数值模拟方案基础上，增加样本量以提升数值模拟及数据分析的可靠性。分别增设0、5、10、15、20、25 ms 共6 组逐孔起爆微差时间，并在六号墩相对于七号墩同样位置处增设11＃～15＃共5 个测点，在第六跨梁远离爆源的另半跨梁体上对称增设16＃～20＃共5 个测点，共计20 个测点，测点编号及位置如图5 所示。分别计算得到20 个测点在6组微差时间下的爆破振速时程曲线。提取这120 组振速时程曲线的峰值，进行不同微差起爆时差条件下邻近高铁桥梁的爆破振动响应分析。

3.1 微差时间对桥梁振速响应的影响规律

将1＃测点分别在6组微差时间下的振速响应峰值绘成散点形式，并用样条曲线连接。对2＃～10＃测点进行同样操作，结果如图6(a)所示；对11＃～2 0＃测点进行同样操作，结果如图6(b)所示。10条不同颜色的曲线，分别代表10 个不同测点处的综合振速峰值随不同微差时间的变化规律。

由图6 分析可知:

1) 1＃～10＃测点和11＃～20＃测点分布规律相近，故振速响应随微差时间的变化规律大致相同。

2) 综合测点处振速峰值随微差时间变化规律有两种类型:随微差时间的增加而快速下降，随后微差时间继续增加时趋于平缓，成波浪状微微起伏，此规律对应的是1＃、3＃、4＃、6＃、10＃测点和11＃、13＃、14＃、16＃、20＃测点，其中，1＃、3＃、4＃、11＃、13＃、14＃测点分布在桥墩上，6＃、10＃、16＃、20＃测点分布在跨梁上；没有随微差时间增加而快速下降的阶段，在微差时间增加的全程均缓慢上升或下降，成波浪状微微起伏，对应的是2＃、5＃、7＃、8＃、9＃测点和12＃、15＃、17＃、18＃、19＃测点，其中，2＃、5＃、12＃、15＃测点分布在桥墩上，7＃、8＃、9＃、17＃、18＃、19＃测点分布在跨梁上。

进一步分析可知:

1) 微差时间对邻近桥梁的振速响应有显著影响，但只集中在一个区间范围内，超出此区间，则微差时间对振速响应影响不显著。炮孔之间微差时间若过小，则接近于同时起爆；若过大，则接近于逐孔起爆。数值模拟结果及试验测试数据分析表明，炮孔微差时间很小或很大情况下，改变微差时间来控制爆破振动响应的效果均不明显。本工程背景下对邻近桥梁振速响应有显著影响的微差时间取值范围是0～5 ms，而5～10 ms 则是一个下降到上升的过渡阶段，这里存在一个极小值。

2) 针对不同位置处的测点，对其振速峰值有显著影响的微差时间区间范围不同。

3)随着微差时间的增加，结构振速响应的变化并非成单调递增或递减趋势，而是反复增减，故总存在一个振速响应的极小值。

3.2 空间位置对桥梁振速响应的影响规律

以微差时间为控制变量，研究测点所处空间位置对测点处振速响应的影响规律。列出在6 组微差时间下邻近桥梁七号墩上1＃～5＃测点振速响应的空间分布规律，如图7(a)所示；六号墩上11＃～15＃测点振速响应的空间分布规律如图7(b)所示。第六跨梁上6＃～10＃测点振速响应的空间分布规律如图8(a)所示；16＃～20＃测点振速响应的空间分布规律如图8(b)所示。7 种不同颜色的曲线中，前6 条分别代表在6 组不同的微差时间下各测点的振速分布规律，第7 条曲线代表地表振速峰值随爆心距呈指数衰减的规律曲线[14]:

式中:v为爆破振动质点最大振速，cm/s；Q为炸药量，kg，齐爆时取总药量，延时起爆时取单段最大药量；R为爆源的距离，m；d为比例距离；K和α分别为爆源至测点间地形、地质条件的相关系数和衰减指数。

由数据分析可知:

1) 从第7 条曲线分析可知，1＃～5＃测点的振速响应随微差时间的变化规律大致和11＃～15＃测点的振速响应随微差时间的变化规律相同；6＃～10＃测点的振速响应随微差时间的变化规律大致和16＃～20＃测点的振速响应随微差时间的变化规律相同；再次印证了所采用数值模拟方案的正确性。

2) 跨梁上测点振速起初随测点离爆源的距离增加而减小，但最远的靠近桥墩顶处的跨梁上测点的振速反而增大，存在一定程度的高程放大效应。

由此可知，邻近高铁桥梁受爆破作用后的振速响应不仅和爆破作用大小有关，也和结构所受约束条件有关，在桥墩底部和主梁靠近墩顶处这些端部固结位置，会出现离爆源较远的地方振速响应反而增大的情况，在爆破安全校核过程中应予以重视，确保爆破安全。