45 t轴重重载铁路扣件系统刚度分析
2022-10-10薄栋乾宋卓西郭恭兵
薄栋乾,韦 凯,宋卓西,郭恭兵,王 显
(1.西南交通大学高速铁路线路工程教育部重点实验室,成都 610031; 2.西南交通大学土木工程学院,成都 610031)
引言
随着科技水平不断提高,重载铁路向大轴重、长编组和大牵引总重的运输方式发展,而提高轴重是重载列车降低运行成本最有效的措施[1]。目前,在重载铁路发达国家,如美国、澳大利亚等已开行36~40 t轴重重载列车[2],未来重载列车轴重仍有进一步提高的趋势。
随着列车轴重不断提高,扣件系统刚度随之进行不断调整[3-6]。王琪[7]通过对比分析27 t与25 t轴重对轨道结构的受力影响,对扣件系统适应性进行了分析并提出相应的强化对策;徐浩等[8]建立了重载货车-无砟轨道-桥梁耦合动力学模型,研究32.5 t轴重重载铁路桥上长枕埋入式无砟轨道扣件系统参数;许良善[9]通过建立车辆-轨道动力学模型及进行有砟轨道实尺模型试验,对35~40 t轴重重载铁路轨道强度进行了研究;杨吉忠等[10]分别使用车辆-轨道耦合动力学理论及基于显式有限元方法的轮轨瞬态滚动接触理论分析模型,计算不同频率下的轨道动态响应,提出了40 t轴重重载铁路扣件的最优动态刚度范围。
综上,国内对于25 t轴重重载铁路扣件系统刚度设计已有较为成熟的设计经验,对于35~40 t轴重重载铁路也开展了一定研究,但针对更高轴重(如45 t)的研究较少。而目前已开始对澳大利亚等国家出口45 t轴重列车[11-12],如扣件系统刚度不能适应该高轴重,将对轨道结构造成疲劳伤损等不良影响,从而严重影响重载铁路运输效率,因此,有必要对45 t轴重重载线路扣件系统刚度展开相关研究。基于45 t轴重重载铁路,首先通过钢轨容许应力法及轨道容许变形法对扣件系统静刚度范围进行合理分析;然后建立重载货车-有砟轨道空间耦合动力学模型,计算不同轮轨激扰、不同刚度条件下车轨耦合系统的动力响应,从而分析扣件系统合理动刚度范围。研究成果可供大轴重重载铁路扣件系统刚度设计参考。
1 扣件系统静刚度分析
1.1 钢轨容许应力法
由强度设计准则,钢轨在重载列车作用下产生的弯曲应力应小于其容许应力,容许应力法即通过钢轨容许应力计算扣件系统静刚度。
钢轨容许应力与钢轨支座刚度关系[13]如下
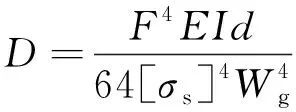
(1)
式中,D为钢轨支座刚度;F为集中荷载;Wg为钢轨下部断面系数;EI为钢轨抗弯刚度;[σs]为钢轨容许应力;d为轨枕间距。
(2)
式中,σs为钢轨屈服极限;K为安全系数。
有砟轨道钢轨支座刚度D由扣件系统静刚度D1、有砟道床刚度D2及路基刚度D3串联而来,即
(3)
则扣件系统静刚度与钢轨容许应力关系为
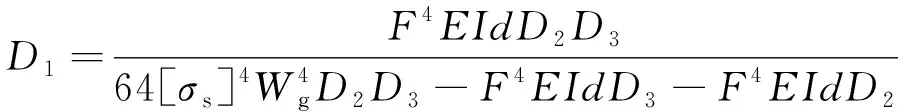
(4)
相关计算参数如表1所示[14]。

表1 扣件系统静刚度计算参数
经计算,扣件系统静刚度为36.1 kN/mm。重载列车作用下钢轨弯曲应力远小于钢轨容许应力,因此,该计算得到的刚度值为扣件系统静刚度最小值。
1.2 轨道允许变形法
轨道在重载列车垂向荷载作用下会产生下沉变形,其计算公式为
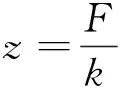
(5)
式中,z为钢轨下沉位移;F为集中荷载;k为轨道整体刚度。
钢轨下沉位移较小时,轨道承受列车荷载较大,会加快轨道部件的伤损;轨道下沉位移较大时,会使轨下基础累积塑性变形加大,增加维修工作量,因此,钢轨下沉位移存在一个合理范围。参考国内外重载铁路有砟轨道钢轨下沉位移限值,45 t轴重重载铁路线钢轨下沉位移的允许范围为2.5~3.3 mm。
而钢轨支座刚度D与轨道整体刚度k的关系如下
(6)
式中各项参数含义同式(1)。联立式(4)~式(6),则可得钢轨下沉位移与扣件系统静刚度的关系如下
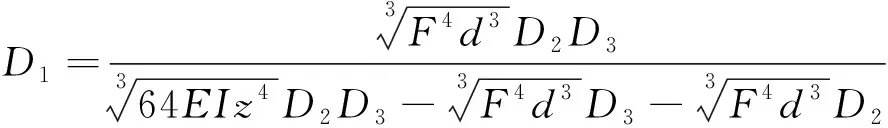
(7)
鉴于有砟道床刚度随时间、密实程度变化会发生改变,为保证在不同道床刚度下钢轨下沉位移均能满足设定的位移范围,参考实测道床稳定区的道床刚度,通过式(7)计算不同道床刚度及扣件系统静刚度条件下的钢轨下沉位移,如图1所示。其中,扣件系统静刚度取值范围为80~800 kN/mm,道床刚度取值为80~170 kN/mm。
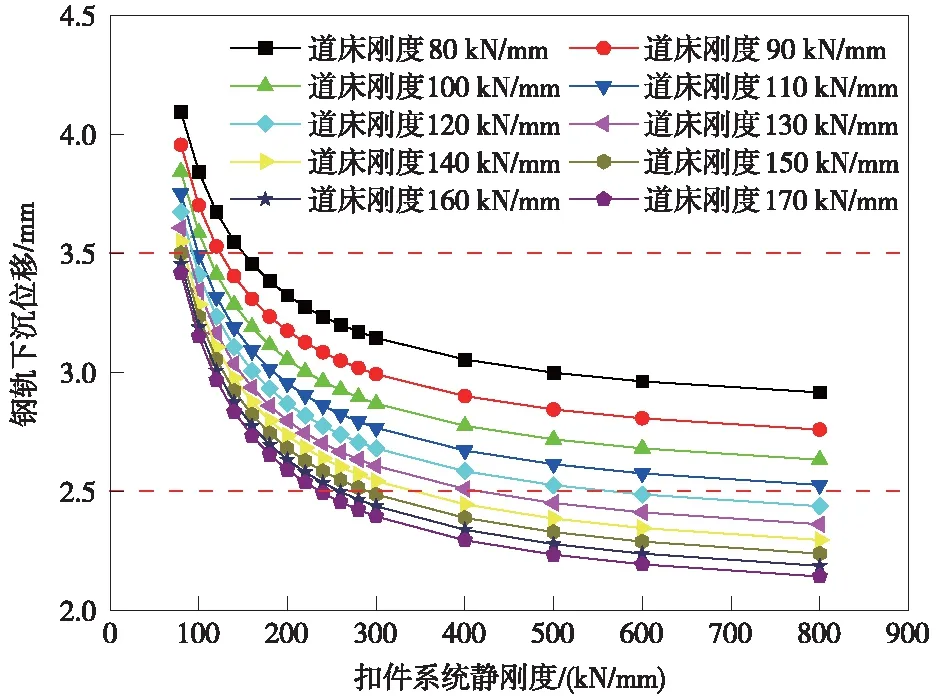
图1 不同扣件系统静刚度下钢轨下沉位移曲线
由图1可知,道床刚度一定时,随着扣件系统静刚度增大,钢轨下沉位移不断降低,且下降趋势逐渐变缓。以道床刚度处于120 kN/mm时为例,当扣件刚度从80 kN/mm增加至200 kN/mm,钢轨下沉位移从3.67 mm降低至2.87 mm,减少0.80 mm;而当扣件刚度从200 kN/ mm增加至800 kN/ mm,钢轨下沉位移从2.87 mm降低至2.44 mm,仅减小0.43 mm,表明当扣件系统静刚度处于80~200 kN/mm范围时,钢轨下沉位移受其影响波动较大。
为使钢轨下沉位移处于2.5~3.5 mm设定范围内,且使其处于稳定状态,建议扣件系统静刚度范围为200~240 kN/mm。
综合钢轨容许应力法及轨道容许变形法,45 t轴重重载有砟轨道扣件系统静刚度应处于200~240 kN/mm范围内。
2 扣件系统动刚度分析
由于扣件系统垫板自身高分子特性,其静态力学性能与动态力学性能呈现明显差异性[17]。因此,通过建立车辆-轨道空间耦合动力学模型,获取不同轮轨系统激扰下、不同扣件刚度条件下45t轴重货车运营时的动力响应,进而分析扣件系统动刚度的合理取值范围。
2.1 车辆-轨道耦合动力学模型
图2为建立的重载货车-有砟轨道空间耦合动力学模型。货车模型由单个车体、2个摇枕、4个侧架及4个轮对构成,车体及轮对考虑横移、沉浮、侧滚、点头及摇头5个运动自由度,摇枕仅考虑摇头运动自由度,侧架考虑横移、沉浮、点头及摇头4个运动自由度。
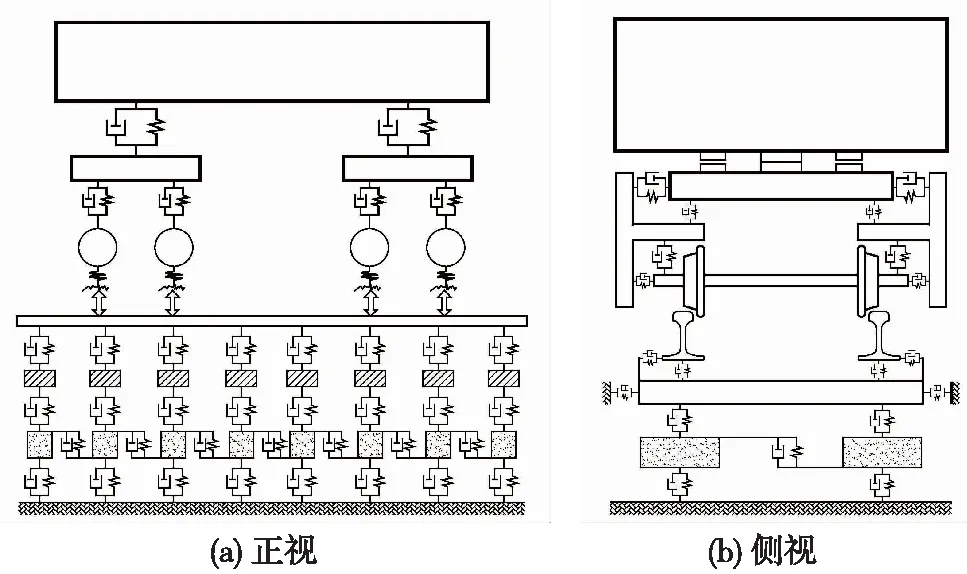
图2 重载货车-有砟轨道空间耦合动力学模型
有砟轨道模型由钢轨、轨枕、有砟道床及路基构成,左右两股钢轨均视为连续弹性离散点支承基础上的Timoshenko梁,考虑垂向、横向及扭转自由度;轨枕视为刚体,考虑垂向、横向及转动运动自由度;道床视为刚性质量块,仅考虑垂向运动自由度[18]。
车轨耦合模型中,轮轨接触模型的合理选择对计算结果存在较大影响,本次计算中,应用Hertz非线性弹性接触理论确定轮轨间法向作用力;轮轨间蠕滑力首先按Kalker线性理论计算,然后进行非线性修正。
2.2 轮轨激励及评价指标
轮轨系统激扰是引起车辆-轨道耦合系统振动的根本原因,在重载铁路中,最主要的是轨道不平顺及钢轨焊缝不平顺[19-20]。分别以美国五级谱及钢轨焊缝不平顺作为激励,研究货车运行速度为90 km/h,扣件刚度在60~600 kN/mm范围变化时轮轨动态响应变化规律,从而提出45 t轴重重载铁路扣件系统动刚度合理范围。
(1)美国五级谱
对于重载铁路,采用美国五级谱作为耦合系统的轨道不平顺输入,波长范围取1~30 m,其时域随机不平顺样本沿线路里程分布如图3所示。
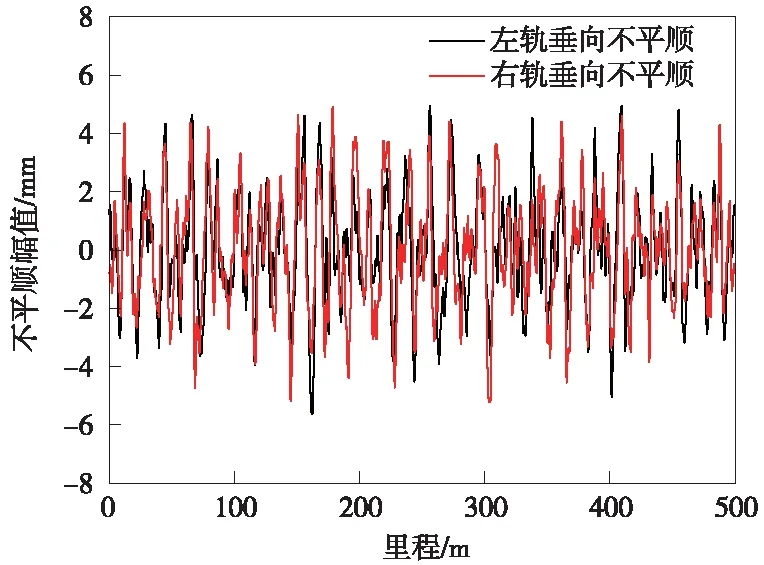
图3 美国五级谱样本
(2)焊缝凹陷不平顺
焊缝凹陷不平顺如图4所示,分为焊缝处和软着区两部分,可采用组合余弦模型描述。
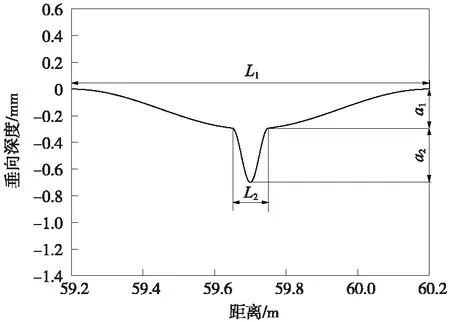
图4 焊缝凹陷不平顺
当0≤x≤(L1-L2)/2,(L1+L2)/2≤x≤L1时
当(L1-L2)/2≤x≤(L1+L2)/2时
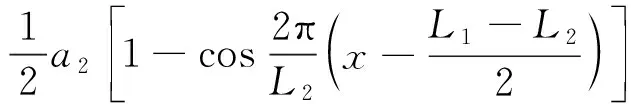
(8)
式中,Z0(x)为焊缝凹陷不平顺值;a1为长波波深;a2为短波波深;L1为长波波长;L2为短波波长;x为车辆运行距离。考虑最不利情况,a1取0.3 mm,a2取0.4 mm,L1取1 m,L2取0.1 m。
(3)评价指标
重载货车动力响应采用轮重减载率评价,其值不应大于0.8;有砟轨道动力响应采用轮轨垂向力、钢轨垂向位移及枕上压力评价,其中,钢轨垂向位移不应超过3.3 mm,枕上压力不应超过196.0 kN[21]。
2.3 动力响应分析
(1)美国五级谱
图5给出了美国五级谱激励下,不同扣件系统动刚度下的车轨耦合系统各项动力响应,由于各刚度下响应曲线非常相似,图中只给出了60,300,600 kN/mm刚度下的动力响应曲线。

图5 美国五级谱激励下轮轨动力响应
由图5可知,在美国五级谱激励下,除钢轨垂向位移随扣件系统动刚度增大而减小外,其他3个指标均随刚度增大而增大。这是因为扣件系统刚度越大,簧下质量引起的动态应力越大,而轨道变形越小。
随着扣件系统动刚度由60 kN/mm增加至600 kN/mm,轮轨垂向力最大值由331.0 kN增大至361.8 kN,增长9.3%;枕上压力最大值由89.1 kN增大至106.0 kN,增长19.0%;钢轨垂向位移最大值由2.62 mm减小至1.07 mm,减少59.2%;轮重减载率最大值由0.49增大至0.7,增长42.9%,可见扣件系统动刚度对美国五级谱引起的轮轨冲击力、枕上压力影响较小,而对钢轨垂向位移、轮重减载率影响较大。
(2)最大动力响应汇总
因钢轨焊缝不平顺动力响应曲线与美国五级谱相似,在此仅绘制4种指标最大值在不同扣件刚度作用下的变化曲线,如图6所示。

图6 两种工况最大动力响应汇总
由图6统计出各动力响应变化率如表2~表4所示。
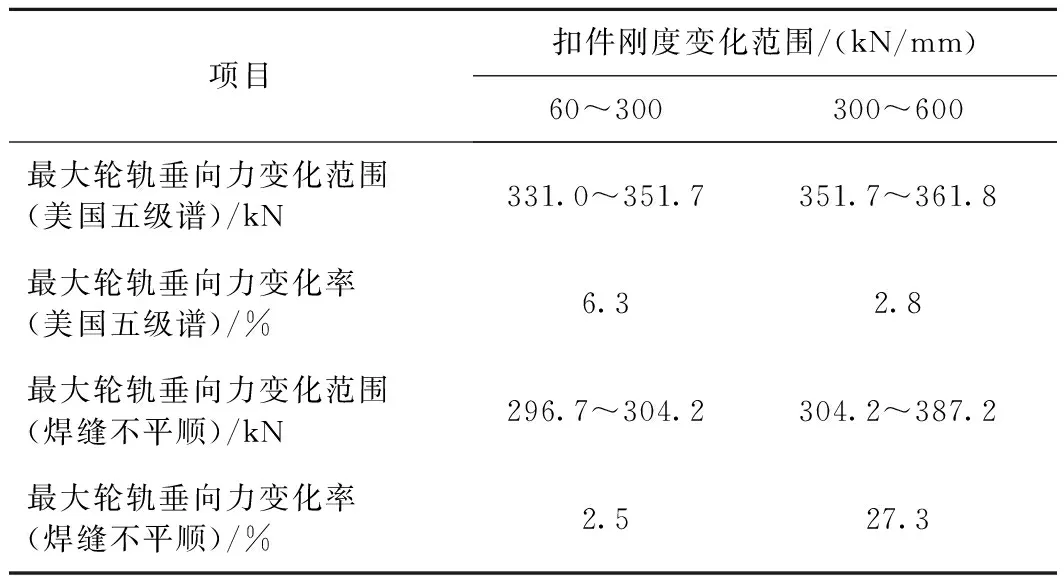
表2 最大轮轨垂向力变化率
由图6(a)可知,在钢轨焊缝不平顺激励下,最大轮轨垂向力先随扣件系统动刚度缓慢增加,而当刚度达到300 kN/mm后陡然上升。由表2可知,当扣件刚度由60 kN/mm增至300 kN/mm、由300 kN/mm增至600 kN/mm时,最大轮轨垂向力增长率分别为2.5%、27.3%。且从图6(d)看出,在钢轨焊缝不平顺激励下,最大轮重减载率在扣件刚度300 kN/mm时达到了0.76,逼近轮重减载率限值0.8。鉴于轮轨垂向力是引起车轨耦合系统随机振动、冲击、疲劳破坏的直接根源,直接影响到列车运行平稳性和安全性[22],出于以上两方面考虑,建议扣件系统动刚度不超过300 kN/mm。最大枕上压力变化率见表3。

表3 最大枕上压力变化率
由表3可知,在美国五级谱激励下,当扣件系统动刚度由60 kN/mm增至180 kN/mm时,最大枕上压力由89.1 kN增至99.2 kN,增长率为11.3%;当刚度从180 kN/mm增至300 kN/mm及300 kN/mm增至600 kN/mm时,其增长率分别为3.9%及2.8%。而在钢轨焊缝不平顺激励下,最大枕上压力增长率依次为12.5%、8.5%及28.7%。综合两种工况,为避免枕上压力过大影响轨下部件的使用寿命,且使其处于一个较为稳定的状态,建议扣件系统动刚度范围为180~300 kN/mm。最大钢轨垂向位移变化率见表4。
由表4可知,当扣件刚度由60 kN/mm增至240 kN/mm时,美国五级谱激励下最大钢轨垂向位移减少率为52.3%,钢轨焊缝不平顺激励下减少率为41.6%。而当刚度从240 kN/mm增至600 kN/mm时,美国五级谱激励下最大钢轨垂向位移从1.25 mm降低至1.07 mm,减少率为14.4%;钢轨焊缝不平顺激励下最大钢轨垂向位移从1.49 mm降低至1.27 mm,减少率为14.8%。为使钢轨位移处于一个较小的水平且受刚度波动影响较小,扣件系统动刚度应不小于240 kN/mm。
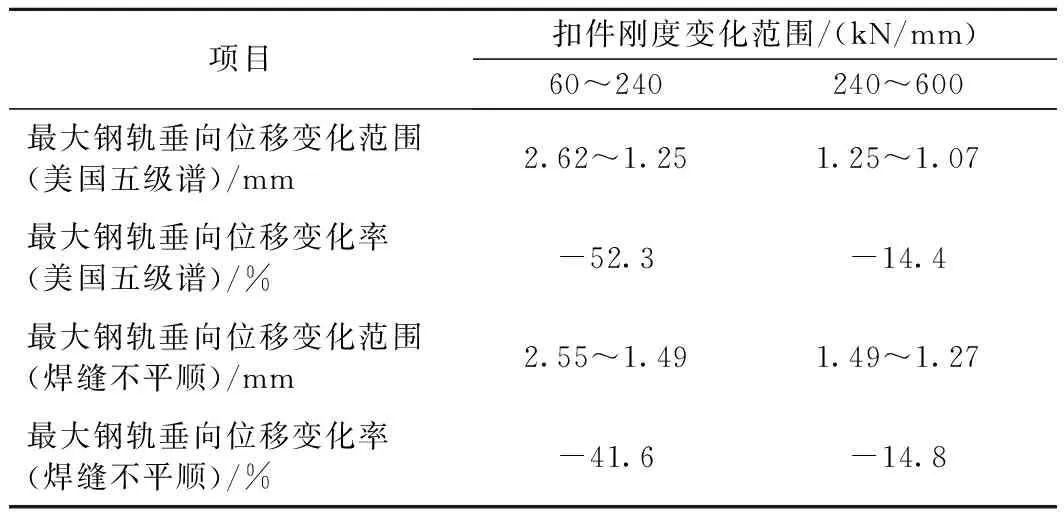
表4 最大钢轨垂向位移变化率
综上,建议45 t轴重重载铁路有砟轨道扣件系统动刚度范围为240~300 kN/mm。
3 结论
通过钢轨容许应力法及轨道容许变形法,分析45 t轴重重载铁路有砟轨道扣件系统静刚度合理取值范围,建立45 t轴重重载货车-有砟轨道空间耦合动力学模型,分析在不同轮轨系统激扰、不同扣件刚度下该耦合系统动力响应变化,提出了扣件系统动刚度合理取值范围。主要结论如下。
(1)为使不同道床刚度范围内的钢轨下沉位移均能满足2.5~3.3 mm要求,扣件系统静刚度范围应为200~240 kN/mm。
(2)在美国五级谱激励下,除钢轨垂向位移随扣件系统动刚度增大而减小外,其他3个指标均随刚度增大而增大,且扣件系统动刚度对轮轨垂向力、枕上压力影响较小,而对钢轨垂向位移、轮重减载率影响较大。
(3)通过综合比较最大轮轨垂向力、最大枕上压力、最大钢轨垂向位移及最大轮重减载率4个指标在美国五级谱及钢轨焊缝不平顺激励下,不同扣件系统动刚度的变化范围,建议扣件系统动刚度范围为240~300 kN/mm。
