基于BDS信噪比的潮位监测精度分析与评估
2022-10-10郑乃铨陈灵秋张乾坤
郑乃铨 陈 鹏 陈灵秋 李 政 张乾坤
1 信息工程大学地理空间信息学院,郑州市科学大道62号,450001 2 西安科技大学测绘科学与技术学院,西安市雁塔中路58号,710054 3 武汉大学测绘学院,武汉市珞喻路129号,430079
GNSS-IR技术旨在分析GNSS卫星发射的信号并通过接收机捕获反射信号,来探索地球表面信息[1]。利用GNSS-IR技术监测潮位是近年来研究的热点。Martin-Neira[2]首次将卫星直射信号和反射信号组合应用于海洋测高。Löfgren等[3]和Larson等[4]证明GNSS接收机接收到的信号中包含部分反射信号,可以用来监测潮位。张双成等[5]利用GNSS-MR进行潮位反演研究,所得结果与验潮站实测数据差值的均值约为10 cm,相关系数优于0.98。Jin等[6]首次利用BDS-IR进行SNR、载波相位和码相位组合估算海平面变化,结果表明,SNR和载波相位组合反演的海平面变化具有良好的一致性,相关系数为0.83~0.91,RMSE小于0.6 m。Wang等[7]使用BRST站的SNR数据进行研究发现,S5X/S2X、S2P/S2C、S5X和S7I分别具有GPS、GLONASS、Galileo和BDS的最佳潮位监测精度。
为评估BDS的潮位监测精度,本文以MAYG站为例进行BDS-IR潮位监测研究,并与GPS的监测精度进行对比分析。
1 BDS-IR监测潮位的原理与方法
MAYG站位于非洲东海岸的Dzaoudzi市,坐标12.782 1°S、45.258 2°E,采样间隔为30 s。测站2 m远处设有Dzaoudzi验潮站,可提供实测潮位数据,采样间隔为1 min。图1给出MAYG站高程基准转换以及BDS-IR监测潮位示意图[8]。天线相位中心到零基准面的高程H为8.432 6 m,当求得RH之后,便可将BDS-IR监测的潮位归算到验潮站同一基准下。本研究的海域高度角为5°~20°,海域方位角为0°~180°和330°~360°。
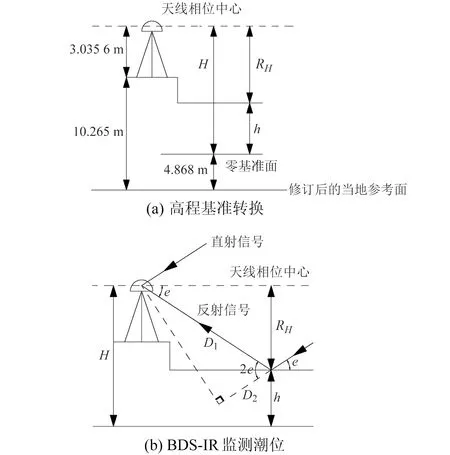
图1 高程基准转换以及BDS-IR技术监测潮位示意图Fig.1 Diagram of elevation datum conversion and BDS-IR for tide level monitoring
利用BDS-IR技术监测潮位的实质就是利用SNR来计算天线相位中心到海平面的垂直反射距离。
卫星信号在传播过程中的路径延迟D为:
(1)
式中,RH为天线相位中心到海平面的垂直反射距离,e为卫星高度角,D1为反射信号从海面反射点到接收机的路程,D2为海面的入射信号比接收机接收到的直射信号少走的路程。
合成信号的SNR由反射信号的SNR和直射信号的SNR组成,3者关系为:
(2)
式中,Ac为从观测文件中提取的合成信号,Ad为直射信号,Am为反射信号,φ为直射信号与反射信号的相位差。由于Ad≫Am,采用二阶多项式拟合法从合成信号中提取直射信号,重采样后通过作差法获取反射信号SNR(δSNR)。
图2给出2020年doy360的SNR变化以及δSNR随高度角的变化。可以看出,BDS2-GEO卫星高度角没有变化,δSNR没有多路径振荡,通过二阶多项式拟合难以提取出多路径效应的影响,因此BDS-GEO无法用于岸基测高。低高度角时多路径效应对SNR值的影响较为明显,因此可以利用低高度角条件下的SNR进行地表环境参数的监测建模,这就是基于SNR的岸基BDS-IR卫星遥感技术的核心原理。
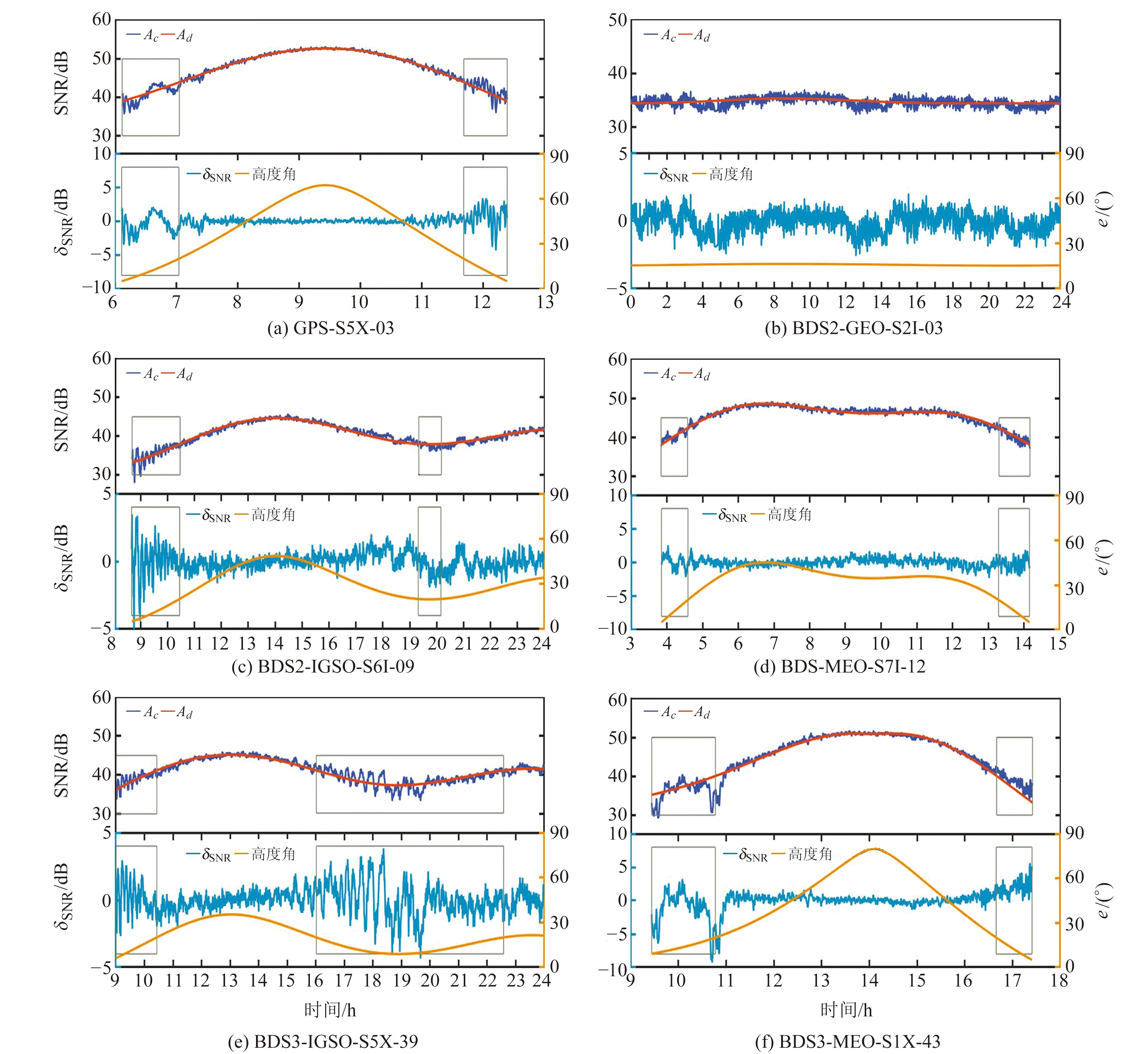
图2 SNR的变化和δSNR随高度角的变化Fig.2 SNR variations and δSNR variations with elevation angle
δSNR的时间序列可用余弦函数表示为:
δSNR=Acos(2πfsine+φ)
(3)
式中,A为振幅。由LSP(lomb-scargle periodogram)频谱分析可得到周期信号功率的最大值对应的频率f,进而求得RH:
(4)
MAYG站SNR类型的频率参数见表1。

表1 MAYG站GPS和BDS的SNR类型及其频率参数
BDS-IR反演的海平面高度为:
(5)
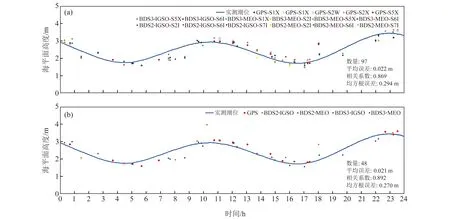
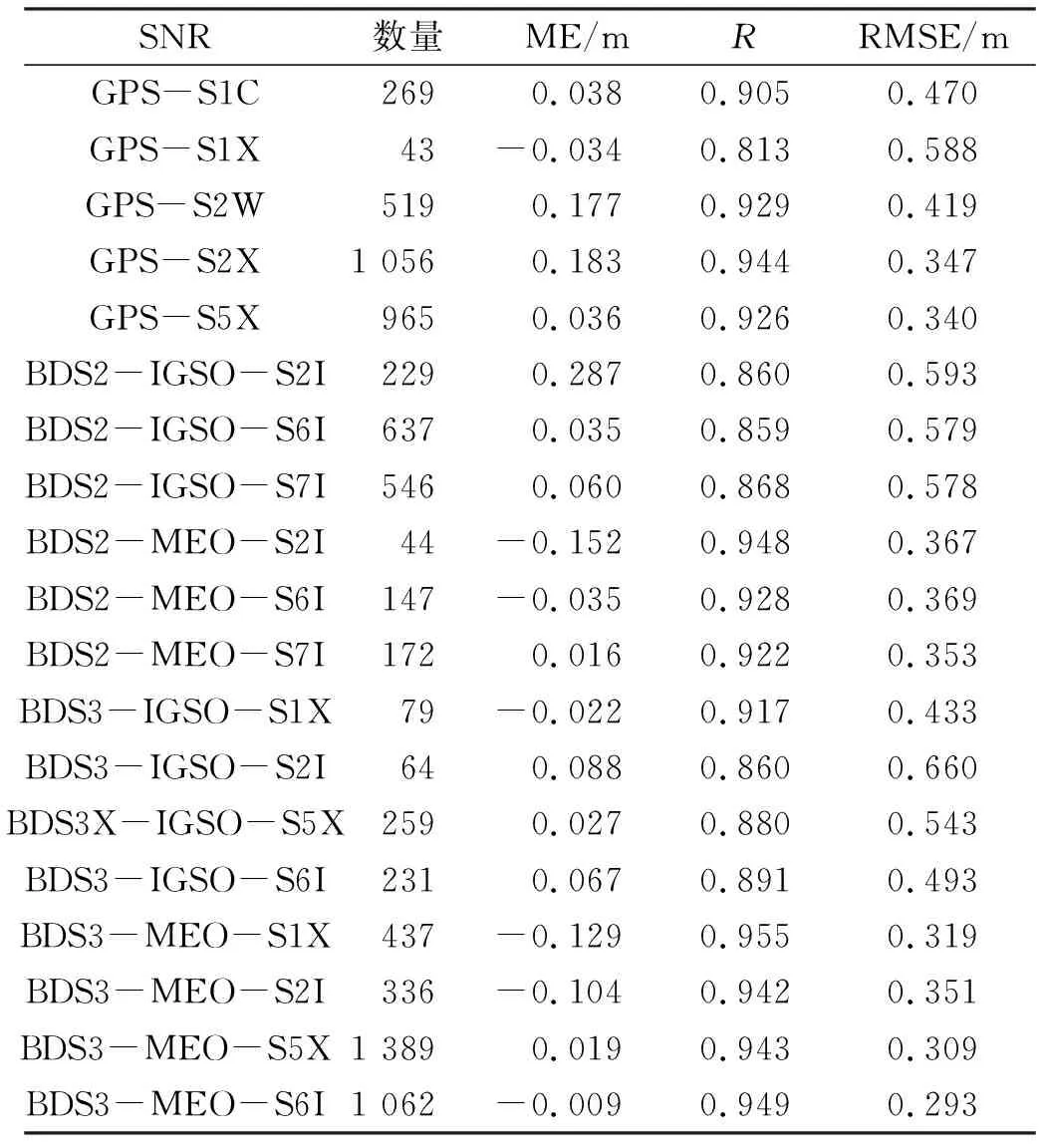
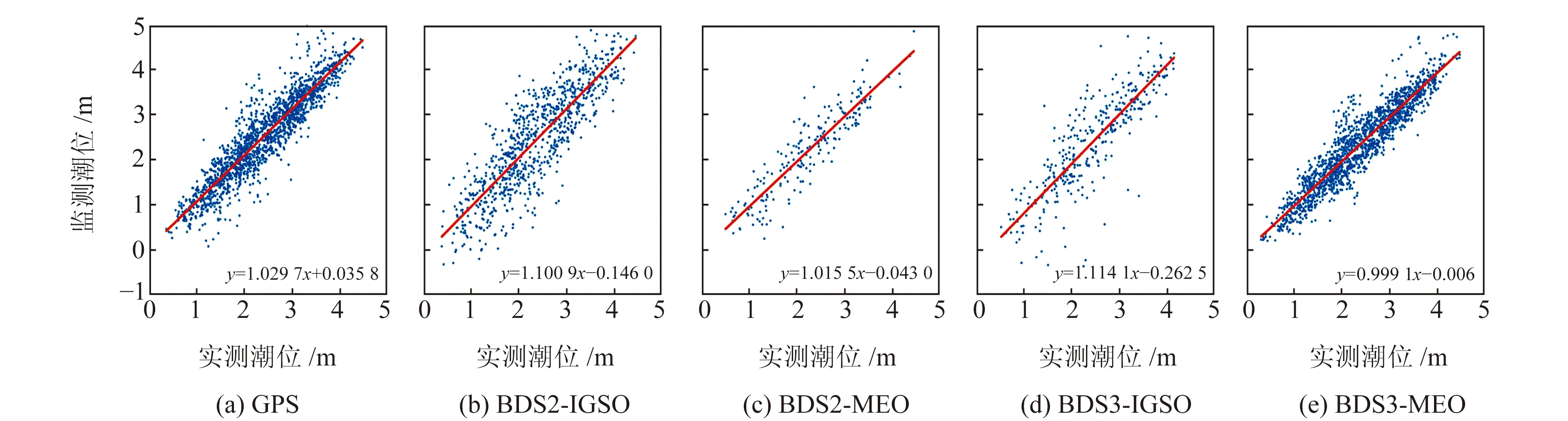
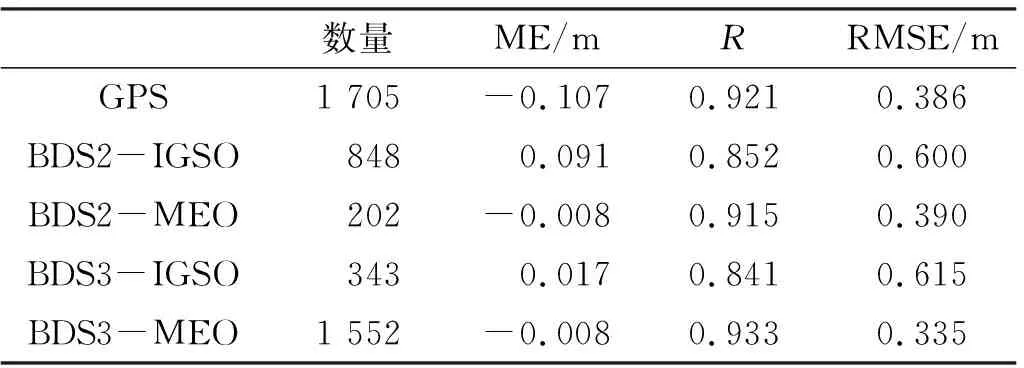
图3给出2020年doy360δSNR随高度角正弦值的变化以及对应的LSP频谱分析示意图。一段δSNR序列仅能反演出一个频率,即对应一个RH,通常取δSNR在时间序列上的平均时间作为瞬时时刻,进而得到BDS-IR在时间序列上监测所得的海平面高度。同一系统不同SNR的δSNR反演的海平面高度时间是一致的。通过最大振幅峰值与噪声振幅均值的比值>3排除δSNR的频率显著性不明显的弧段,通过3.5 m 图3 δSNR随着高度角正弦值的变化以及LSP频谱分析Fig.3 δSNR variations with sin of elevation angle and spectral analysis of LSP 图4(a)给出MAYG站doy360的GNSS-IR监测潮位与验潮站实测潮位对比,图中曲线为实测潮位,散点为不同SNR类型监测得到的潮位。可以看出,监测潮位均匀分布在实测潮位附近,两者具有较好的一致性。经实验可得,该天监测数量为97,平均误差ME为0.022 m,相关系数R为0.869,RMSE为0.294 m。为了避免信息冗余,将不同SNR类型反演的同一时刻的潮位取均值。从图4(b)中可得,该天监测数量为48,ME为0.021 m,R为0.892,RMSE为0.270 m。不同SNR类型均值处理后监测数量大为缩减,这样既可避免了信息冗余,又保证一定的反演精度。 图4 2020年doy360 GPS-IR、BDS-IR监测潮位与验潮站实测潮位对比Fig.4 Comparison of the tide level monitored by GPS-IR, BDS-IR and measured by the tide gauge station on doy 360, 2020 利用MAYG站2020年doy268~366期间BDS3的IGSO和MEO卫星SNR数据分析BDS3潮位监测的精度,并与BDS2和GPS进行对比,见表2。分析RMSE可知,GPS的精度为S5X>S2X>S2W>S1C>S1X,BDS2-IGSO的精度为S7I>S6I>S2I,BDS2-MEO的精度为S7I>S2I>S6I,BDS3-IGSO的精度为S1X>S6I>S5X>S2I,BDS3-MEO的精度为S6I>S5X>S1X>S2I。BDS3-MEO-S6I潮位监测的精度明显优于其他SNR类型潮位监测的精度,证实BDS3监测潮位具有较高的可靠性。分析ME的绝对值可知,BDS3-MEO-S6I最小,BDS2-IGSO-S2I最大,这可能与IGSO的卫星轨道持续时间比其他卫星星座更长有关。分析R可知,GPS-S1X的最小,这可能与该SNR类型的卫星数量较少有关,BDS3-MEO-S1X的最大。综上所述,BDS3-MEO-S6I的海面高度监测效果最好,BDS3-IGSO-S2I的海面高度监测效果较差。 表2 2020年doy268~366 SNR监测潮位精度对比 图5给出GPS-IR、BDS2-IR和BDS3-IR去除冗余信息后,监测潮位与验潮站实测潮位的相关性分析。可以看出,BDS不同类型星座的反演结果与实测值均具有较高的一致性,且BDS3卫星的符合度明显高于BDS2卫星,MEO卫星的符合度也明显高于IGSO卫星。 图5 不同SNR类型融合后GPS-IR、BDS-IR和验潮站相关性分析Fig.5 Correlation analysis of GPS-IR, BDS-IR and tide gauge station after fusion of different SNR types 从表3中可以看出,不同SNR类型融合后,就RMSE而言,BDS2和BDS3的监测精度对比结果为BDS3-MEO>BDS2-MEO>BDS2-IGSO>BDS3-IGSO;BDS3-MEO监测精度明显优于GPS。BDS-IGSO监测精度较低可能是因为:1)BDS-IGSO的卫星轨道持续时间比其他卫星星座更长,故与MEO卫星相比,每次反演的海平面的瞬时时刻是更长时间的平均值;2)BDS-IGSO的卫星运行高度要高于BDS-MEO,且BDS-IGSO为24 h地球同步轨道卫星。 表3 SNR融合后GPS-IR、BDS-IR潮位监测精度对比 1)分析单个SNR的精度可得,BDS3-MEO-S6I的海面高度监测效果最好,BDS3-IGSO-S2I的海面高度监测效果最差。 2)BDS2和BDS3的监测精度对比结果为BDS3-MEO>BDS2-MEO>BDS2-IGSO>BDS3-IGSO; BDS3-MEO的监测精度明显优于GPS。BDS-IR反演的瞬时潮位具有较高的精度,与验潮站提供的实测潮位相比具有较好的相关性,能够呈现出海平面高度随时间序列的动态变化,可用于近岸海域潮位监测。 3)BDS-GEO卫星高度角没有变化,δSNR弧段没有多路径振荡,因此BDS-GEO无法用于岸基测高;BDS-IGSO卫星轨道持续时间比其他卫星星座更长,因此BDS-IGSO的潮位监测精度较差。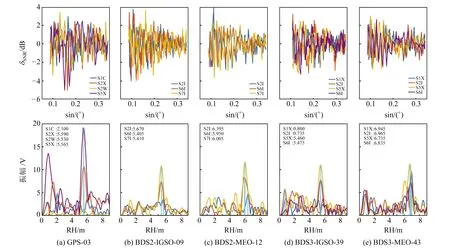
2 实验与分析
3 结 语
