基于神经网络和多标度特征分析的古滑坡变形预测及趋势评价

2022-10-10田倩吴健赵东

大地测量与地球动力学 2022年10期

田倩吴健赵东

1 陕西铁路工程职业技术学院，陕西省渭南市站北街东段1号，714000 2 湖北省地质局第一地质大队，湖北省大冶市湖滨路9号，435000

受人为等不确定因素影响，古滑坡局部复活时有发生。考虑到变形是滑坡复活的直观体现，因此，开展古滑坡变形预测及多标度特征分析具有重要意义[1-3]。目前，已有学者开展古滑坡研究，并取得一定成果[4-7]，但少有涉及古滑坡局部复活的变形特征的研究。

滑坡变形数据一般都含有一定的噪声信息[8]，因此，进行滑坡变形规律研究前，有必要先进行变形数据的分解处理。在滑坡变形规律研究中，基于神经网络的变形预测具有良好的分析效果[9]；多重分形消除趋势波动分析能有效评价变形序列的多标度特征[10]。综上，本文先进行数据分解处理，再通过神经网络实现滑坡变形预测，最后利用多重分形消除趋势波动进行滑坡变形的多标度特征评价及趋势判断，以期为滑坡灾害防治提供理论指导。

1 基本原理

1.1 数据分解模型构建

一般可将滑坡变形监测数据分为趋势性分量和误差性分量，前者代表滑坡变形的真实信息，后者代表滑坡变形的误差信息。误差性分量会在一定程度上影响预测精度，且不利于后续多标度特征研究[8,11]，因此有必要先对滑坡变形数据进行分解处理。

经验模态分解(EMD)模型适用于非平稳、非线性变形数据的分解[12]。但受模型构建原理的限制，其存在一定不足，如分解过程可能存在模态混叠，对分解效果有一定影响。为解决该问题，可以在信息分解过程中引入白噪声信息，即集合经验模态分解(EEMD)模型。但EEMD模型在分解过程中主要是将高频信息进行剔除，这会在一定程度上丢失固态分量的细节信息。为尽可能保留滑坡变形数据的真实信息，在EEMD模型分解处理后，对其固态分量构建Hankel矩阵，并通过奇异值分解(SVD)模型对矩阵进行处理，即通过奇异值求解进行二次滤波处理，以综合消除噪声信息。

综上所述，本文以EEMD模型和SVD模型为基础，构建出组合分解模型EEMD-SVD，以其进行滑坡变形数据的分解处理。

为合理评价数据分解的效果，提出以信噪比、平滑度指标及均方根误差为基础指标，考虑到3个基础指标求解方法的不一致性，用3者的归一化值构建出分解效果的综合评价指标k：

k=k1+k2+k3

(1)

式中，k1、k2、k3分别为信噪比、平滑度指标及均方根误差的归一化值。一般来说，k值越大，分解效果越好。

1.2 预测模型构建

极限学习机(extreme learning machine, ELM)能在保持全局逼近能力的基础上，同时具有较强的泛化能力，相较传统神经网络预测精度高、操作简单，因此利用其构建趋势性分量预测模型。ELM模型训练过程可表示为：

(2)

式中，oj为预测值；L为隐层节点个数；xj为输入值；g(x)为激励函数；βi、wi为连接权值；bi为阈值。但由于连接权值和阈值随机产生，会使ELM模型的预测过程存在初始化问题。为此，提出两步优化原则：1)利用均值极限学习机(MELM)来保证预测结果的稳定性；2)对MELM模型的连接权值和阈值进行优化处理。

首先，由m个相同结构的ELM模型进行随机预测，即可得到m个预测结果，并对每个节点的预测值进行均值求解。其次，考虑到蝙蝠算法(bat algorithm, BA)不仅可利用自身声呐搜索猎物和躲避障碍，还能通过改变自身位置和速度进行全局寻优处理，因此使用BA算法进行连接权值和阈值优化[13]。优化流程如图1所示。

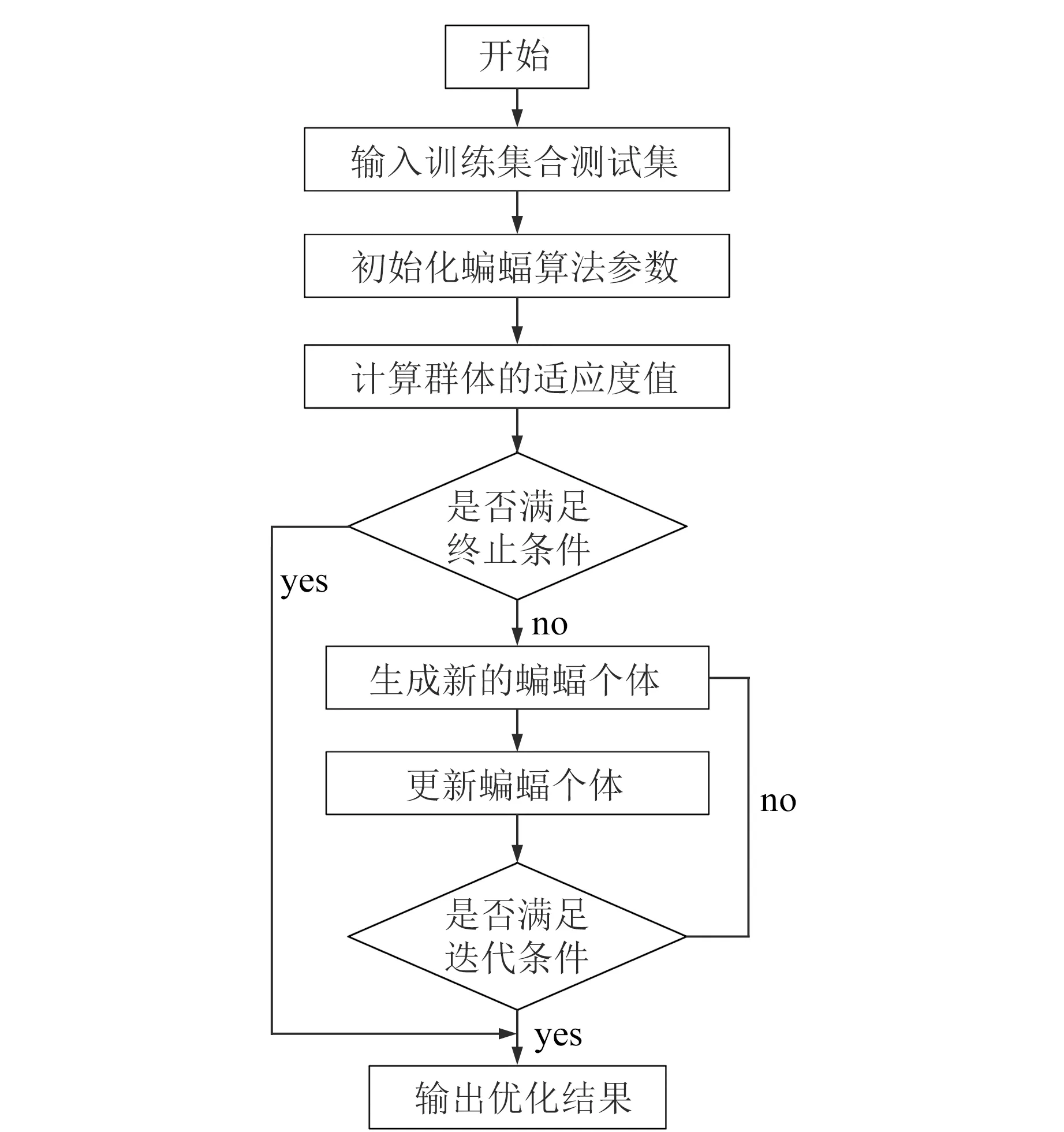
图1 BA算法优化流程Fig.1 The optimization flow chart of BA algorithm

通过前述递进优化处理，可有效保证预测模型参数的最优性，但考虑到趋势性分量的非线性特征，BA-MELM模型仍会存在一定预测误差。将预测误差叠加至误差分量，以得到一个新的变形信息分量，并将此叠加序列命名为噪声分量。

考虑到Arima模型具有很强的误差修正能力，因此利用其实现噪声分量预测，计算公式为：

(3)

式中，Rt为噪声分量预测值；rt-m为对应节点处的噪声分量；p、q为回归阶次；θj为滑动参数；φm为自回归参数；at为对应t节点处的白噪声；at-j为对应t-j节点处的白噪声。

1.3 多标度特征分析模型构建

利用多重分形消除趋势波动分析(multi-fractal detrended fluctuation analysis, MF-DFA)模型评价滑坡变形序列的多标度特征及发展趋势。考虑到趋势性分量可代表滑坡真实变形信息，因此以其作为多标度特征分析的数据基础。结合MF-DFA模型基本原理[10]，先对滑坡变形序列进行区间划分。以滑坡变形数据为基础，先计算其累积离差序列，并将累积离差序列的个数表示为N，子序列长度设置为s，则子序列个数为Ns=N/s；由于N和s并不一定为整数关系，为保证累积离差序列均被分析，在正向子区间划分基础上再进行逆序划分，以得到2Ns个子区间。其次，对波动函数的阶次q进行设定，其波动函数F(q,s)为：

(4)

式中，F2(s,v)为子区间方差值；v为子序列序号。

通过改变子序列长度s可得到对应的F(q,s)值，进而得到若干散点(s,F(q,s))，并利用其构建如下关系：

lnF(q,s)=T+h(q)·lns

(5)

式中，h(q)为Hurst指数；T为常数。

在MF-DFA模型分析过程中，将阶次q设定为-8～8之间的偶数值，通过h(q)随s的变化来判断滑坡变形的多重分形特征：若h(q)值随q值变化而变化，则滑坡变形序列具有多重分形特征；反之，则不具有多重分形特征。同时，h(2)值可作为滑坡发展趋势的评价指标：当h(2)值在[0,0.5)时，滑坡变形具有下降趋势，且h(2)值越小，趋势性越强；当h(2)值等于0.5时，滑坡变形属于游离状态，无法判断其发展趋势；当h(2)值在(0.5,1.0)时，滑坡变形具有增加趋势，且h(2)值越大，趋势性越强。

以q与h(q)值为基础，计算奇异指数a(q)：

a(q)=h(q)+qh′(q)

(6)

式中，h′(q)为h(q)对应的导函数值。

最后，以a(q)为基础，计算Δa和Δf(a)：

Δa=amax-amin

(7)

Δf(a)=Δf(amax)-Δf(amin)

(8)

式中，Δa为多重分形谱宽度；Δf(a)为波形中大小波动所占比例。Δa参数可评价滑坡变形的多重分形谱宽度，其值越小，多重分形宽度相对越弱，即波动会越平稳；Δf(a)参数可评价滑坡变形中各类大小波动所占比例，其值越大，大波动波形所占比例越小。

2 实例分析

2.1 滑坡概况

王家坡滑坡位于西安市灞桥区，具有比较典型的多级古滑坡群地貌，其中，HT02滑坡位于古滑坡体上部，属于古滑坡局部复活带[14]。本文以HT02滑坡为研究对象，开展滑坡变形预测及多标度特征分析。

HT02滑坡平面呈舌状(图2)，高程分布范围为590～675 m，坡度约15°，滑坡纵向长约300 m，横向宽约150 m，面积约0.037 km2，厚度主要在0～31 m，平均厚约18 m，体积约66.6×104m3，属中型土质滑坡。

图2 滑坡平面形状及监测点位置Fig.2 Plane shape of landslide and location of monitoring points

在变形特征方面，HT02滑坡变形主要可划分为道路变形和住宅区变形，具体如下：1)道路变形。道路横穿滑坡中部，其变形主要为道路中部发育有裂缝，裂缝具有持续扩大特征，并以裂缝为界，两侧道路均产生规模不一的不均匀沉降。2)住宅区变形。住宅区主要位于滑坡中部，其变形主要为墙体出现规模不一的裂缝，且裂缝可能延伸至地面，宽度主要为2～10 cm。

为及时掌握滑坡变形特征，在滑坡居民区附近设置2个监测点，具体位置如图2所示。在监测过程中，以滑坡区外的稳定控制点为基础，通过全站仪进行变形监测，监测时间为2018-10～2019-08，以5 d为1期，共得到60期数据，其变形-时间曲线如图3所示。从图3可以看出，2个监测点变形具有持续增加趋势，其中，2#监测点累积变形量相对较大，变形值达185.00 mm，1#监测点累积变形量为130.02 mm。

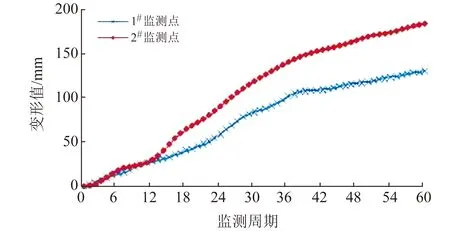
图3 滑坡变形-时间曲线Fig.3 Landslide deformation-time curve

2.2 数据分解处理

使用不同模型对滑坡变形数据进行分解，结果如表1所示。对比EMD和EEMD模型结果可知，EEMD模型的2个监测点的综合评价指标k值均更大，说明EEMD模型较EMD模型具有更优的分解效果。EEMD-SVD模型综合评价指标k值明显大于其他3种单项模型，初步说明组合分解模型较单项分解模型具有更强的数据分解能力。同时，在EEMD-SVD模型分解结果中，1#和2#监测点的综合评价指标k值均趋近于3，说明EEMD-SVD模型在滑坡变形数据中具有良好的分解效果，适用于滑坡数据分解。

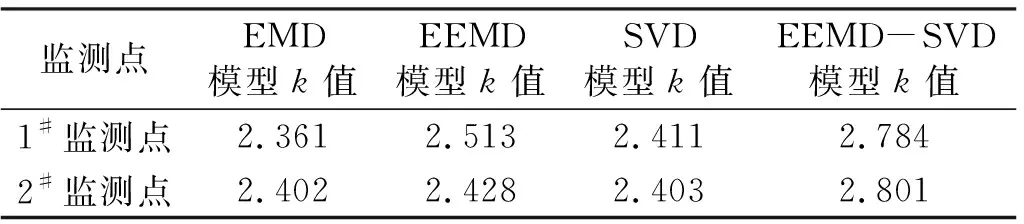
表1 不同组合方法的分解结果

为进一步验证EEMD-SVD模型在滑坡变形数据处理中的优越性，利用小波去噪和卡尔曼滤波进行同样的分解处理，结果如图4所示。可以看出，小波去噪和卡尔曼滤波的综合评价指标k值相当，但明显小于EEMD-SVD模型的综合评价指标k值。说明在本文实例中，小波去噪和卡尔曼滤波模型的分解能力弱于EEMD-SVD模型。

图4 不同模型的分解结果Fig.4 Decomposition results of different models

综上所述，EEMD-SVD模型与传统分解模型相比具有更强的数据分解能力，可用于滑坡变形数据分解。

2.3 滑坡变形预测分析

在前述滑坡变形数据分解处理的基础上，开展滑坡变形的分项组合预测。为充分验证本文预测思路的适用性，将预测过程分为中期和后期：中期使用1～30期变形监测数据，最后5期作为验证样本；后期使用1～60期变形监测数据，最后5期作为验证样本，外推预测设置为4期。

2.3.1 中期预测结果分析

在滑坡中期变形预测过程中，为充分体现分项组合流程的预测效果，以1#监测点为例，详述不同优化阶段的分项预测结果。首先，统计得到趋势性分量的预测结果(表2)。可以看出，ELM模型预测结果的相对误差范围为2.95%～3.17%，平均相对误差为3.06%；MELM模型预测结果的相对误差范围为2.35%～2.73%，平均相对误差为2.56%；BA-MELM模型预测结果的相对误差范围为2.16%～2.34%，平均相对误差为2.26%。对比3类模型的预测结果可知，BA-MELM模型预测精度最高。但BA-MELM模型的平均相对误差值为2.26%，预测效果相对一般，且考虑到误差分量的影响，侧面说明了进行后续噪声修正预测的必要性。

表2 1#监测点趋势性分量预测结果

如前所述，1#监测点的趋势性分量预测结果存在一定预测误差，将预测误差叠加至误差性分量中，以得到噪声分量，并利用Arima模型进行预测处理，得到1#监测点的中期预测结果(表3)。可以看出，通过噪声分量的误差弱化预测，1#监测点在中期预测结果中的相对误差范围为2.09%～2.19%，平均相对误差为2.14%，相较趋势性分量的预测精度略有提高，验证了分项组合预测在滑坡变形预测中的适用性。

表3 1#监测点中期预测结果

类比1#监测点的中期预测过程，对2#监测点进行中期预测，结果如表4所示。可以看出，2#监测点中期预测结果相对误差范围为1.96%～2.19%，平均相对误差为2.10%，预测精度与1#监测点相当，初步验证了本文分项组合预测模型具有较优的稳健性。

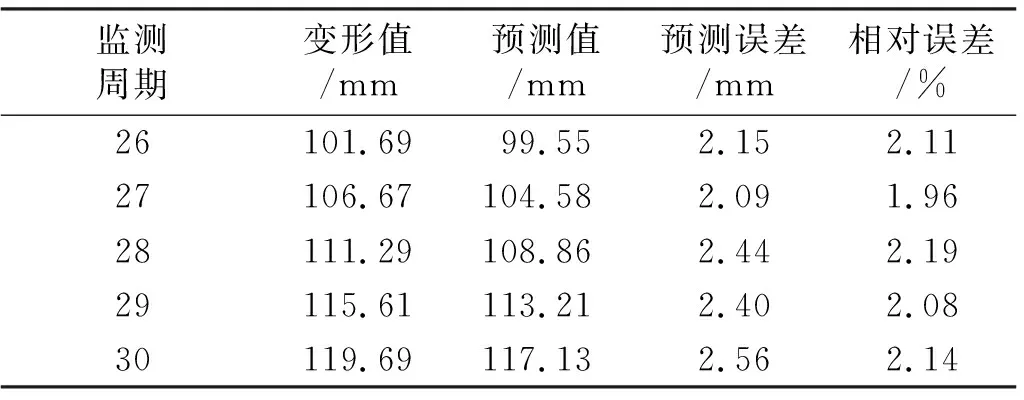
表4 2#监测点中期预测结果

2.3.2 后期预测结果分析

滑坡变形后期预测结果如表5所示。从表5可知，1#监测点后期预测结果的相对误差范围为1.97%～2.06%，平均相对误差为2.02%；2#监测点后期预测结果的相对误差范围为1.95%～2.03%，平均相对误差为1.99%。两者预测精度相当，均在2%左右，具有较高的预测精度，进一步验证了本文分项组合预测模型在滑坡变形预测中的适用性。

2个监测点外推预测结果显示，滑坡变形仍会进一步增加，1#和2#监测点的外推增加速率均值分别为1.36 mm/周期和1.23 mm/周期。

表5 滑坡后期预测结果

为进一步对比本文预测模型对样本数的敏感性，对中期和后期预测结果的平均相对误差进行统计，结果如图5所示。可以看出，不同样本数条件下的预测效果存在一定差异，其中，前期的平均相对误差变化范围为2.10%～ 2.14%，而后期的平均相对误差变化范围为1.99%～ 2.02%。后期的预测精度相对略高，说明本文预测模型对大样本条件下的长期预测具有更优的预测效果。

图5 不同样本数条件下的预测效果对比Fig.5 Comparison of prediction effects under different conditions

综上所述，通过分项组合预测可提高预测精度，且中、后期预测结果均具有较好的预测效果；同时，外推预测结果显示，滑坡变形仍会进一步增加，增加速率为1.23～1.36 mm/周期。

2.4 多标度特征分析

本节利用MF-DFA模型开展滑坡变形的多标度特征分析。首先，以所有监测样本为基础，计算不同波动阶次q条件下的h(q)值，以开展滑坡变形的多重分形特征评价，结果如表6所示。

从表6可见，随着阶次q的增加，h(q)值随之减小，说明滑坡变形序列具有多重分形特征；同时，对比2个监测点的h(2)值可知，1#监测点为0.614，2#监测点为0.592，两者均大于0，表明滑坡后续变形量会进一步增大，且1#监测点的趋势性相对更强，侧面佐证了前述外推预测结果的准确性。

表6 滑坡多重分形特征结果

为进一步掌握滑坡变形趋势的阶段性特征，将滑坡变形监测样本划分为3个阶段(1～20周期、21～40周期、41～60周期)进行分析。对各阶段进行MF-DFA，统计2个监测点在不同阶段的h(2)值，结果如图6所示。可以看出，不同阶段的h(2)值存在一定差异，但均大于0.5，说明随着时间的增加，滑坡变形具有持续增加趋势，只是程度不同，具体表现为趋势性先增加后减小。值得注意的是，在阶段3的趋势判断结果中，1#监测点处的h(2)值相对略大，这与前述整体趋势判断一致，也进一步验证了前述对滑坡变形趋势性判断的正确性。

图6 不同阶段的趋势性对比Fig.6 Comparison of trends in different stages

最后，再对多重分形谱宽度Δa和波形中大小波动所占比例Δf(a)进行统计，以进一步开展滑坡变形的多标度特征分析，结果如表7所示。从表7可知，1#监测点Δa值为0.907，2#监测点Δa值为0.981，后者更大，说明其多重分形宽度相对更宽，波动性相对更强；1#监测点Δf(a)值为0.798，2#监测点Δf(a)值为0.706，前者相对更大，说明2#监测点的大波动波形所占比例相对更大。