大型复杂系统多态可靠性快速评估算法
2022-10-10史跃东金家善
史跃东,金家善,柴 凯
(海军工程大学舰船与海洋学院,湖北 武汉 430033)
0 引 言
可靠性作为一类反映装备通用质量特性的固有属性,直接影响装备的固有性能与使用效能发挥,进而决定装备执行任务的成功与否。研究装备的可靠性,对于改善装备质量特性,优化装备保障管理,增强装备使用效能,提升装备执行任务能力,具有重要工程应用价值与现实经济意义。近年来,随着现代科技与制造业水平的迅猛发展,装备的结构组成日趋复杂,多呈现大型化、集成化、精细化、耦合化等特点。同时,与其相关的可靠性分析、设计、评估等工作,也日趋复杂与困难。为此,衍生出诸多新的可靠性研究方向。装备复杂系统多状态可靠性研究,即为其中比较具有代表性的重点和热点研究方向,且发展迅速、成果丰硕[1-3]。
有关装备复杂系统多状态可靠性的研究工作,大体可分为4类。第1类基于经典马尔可夫状态跃迁模型,通过多粒度割分传统的装备二元功能状态,建立不同状态间的跃迁微分方程,实现装备复杂系统的多状态可靠性建模、分析与评估,但存在指数分布模型假设的工程约束困境[4-7],以及大维度状态跃迁微分方程解算的技术瓶颈[8-11],此外相关系统状态的工程分辨解析程度也大大受到限制[12-15]。第2类基于半马尔可夫状态跃迁模型,通过构建非指数分布约束的嵌入式马尔可夫链,并引入核矩阵函数,有效改善了装备复杂系统的多状态可靠性建模、分析与评估精度[16-18],但仍面临大维度状态解算的技术瓶颈[19-21]。第3类基于通用生成函数技术,通过定义不同结构单元的通用生成函数,并结合系统不同层级间的构型耦合关联,完成装备复杂系统的通用生成函数求解与多状态可靠性解析,有效规避了直接解算大维度状态模型的技术困境[22-25],但本质上仍只是进行了降维变换,对超大系统或巨系统应用效果欠佳[26-29]。第4类基于蒙特卡罗仿真技术,通过生成贴近状态驻留时间随机分布的伪随机量值,模拟装备复杂系统的逻辑事件历程,进而利用数理统计方法,获取多状态装备复杂系统的可靠性能,但对于先验分布的判断以及仿真数据的体量要求较高[30-32]。
综上,4类研究工作虽能较好地解决部分装备复杂系统的可靠性建模、分析与评估问题,并已在当今机械、电力、能源、军事、信息网络等领域发挥了重要作用,但对于组件构成庞大的大型(或巨型)装备复杂系统来说,利用前述4类工作的阶段研究成果,开展其多状态可靠性的分析与评估工作,无论是在计算资源的依赖性上,还是在解算方法的可实现性与便捷性上,都还或多或少地存有技术短板,亟待深入探索、逐步完善。
本文以工程上组件构成众多的大型装备复杂系统为研究对象,旨在通过合理构建面向不同系统状态耦合结构的极限序列核,探索一类计算资源要求低、计算便捷,且逼近精度满足工程需要的多状态可靠性建模、分析与快速评估方法,力求丰富与突破大型装备复杂系统多状态可靠性研究的关注方向和技术途径。
1 大型多状态装备系统
1.1 大型多状态系统
任意大型多状态装备系统A,由k个子系统B i组成,i=1,2,…,k,k∈N;每个子系统Bi包含l i个组成元件U ij,j=1,2,…,l i,l i∈N;系统A使用过程中,元件U ij的输出性能可能逐步退化,存在s+1种输出状态,s∈N;同时,可能有多样作用于系统A的外在载荷,存有p+1种运行工况要求,p∈N;并且有如下前提假设和符号约定:
(1)不同元件U ij的性能退化随机历程可测,且关键退化状态节点的认定规则相似;
(2)系统A与任意元件U ij的输出状态索引集合为{0,1,…,s},其中索引0代表最劣状态,索引s代表最优状态,自索引0至索引s,状态水平依次升高;
(3)系统A的运行工况索引集合为{0,1,…,p},各工况运行可能出现的概率为qz,z∈{0,1,…,p},qz∈[0,1];
(4)u ij(t,z)、a(t,z):第z种 工况下,u ij(t,z)和a(t,z)分别为元件U ij、系统A自最优状态s触发后t时刻所处的状态水平,其中,t∈[0,∞);
(5)T ij(v,z):第z种工况下,元件U ij自最优状态s触发,保持u ij(t,z)∈状态子集{v,v+1,…,s}的独立随机变量,T ij(v,z)反映元件U ij处于不同状态子集的驻留时间。其中,v∈{0,1,…,s};
(6)T(v,z):第z种工况下,系统A自最优状态s触发,保持a(t,z)∈状态子集{v,v+1,…,s}的随机变量,T(v,z)反映系统A处于不同状态子集的驻留时间。其中,v∈{0,1,…,s}。
1.2 多状态系统可靠性
遵循前述假设与符号约定,统一选用可靠度函数R(t)作为度量大型多状态装备系统A可靠性的量化参数,则有:
(1)元件U ij可靠度
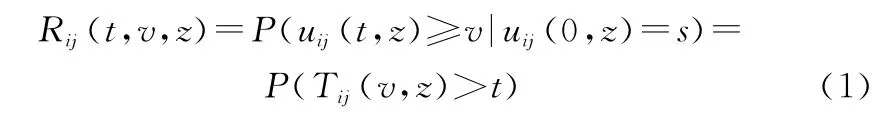
式中:P(·)为绝对概率函数;P(·|·)为条件概率函数;Rij(t,v,z)为z工况下元件U ij处于状态子集{v,v+1,…,s}的可靠度函数。
(2)系统A可靠度
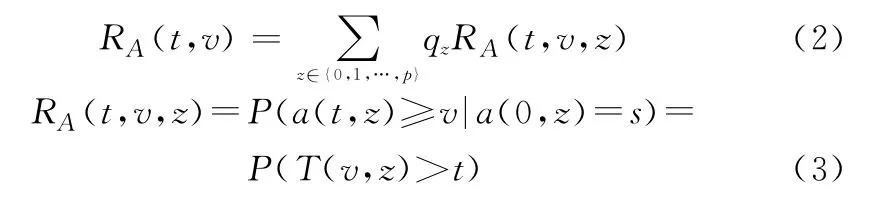
式中:RA(t,v)为系统A处于状态子集{v,v+1,…,s}的可靠度函数;RA(t,v,z)为z工况下系统A处于状态子集{v,v+1,…,s}的可靠度函数。
(3)系统A状态分布
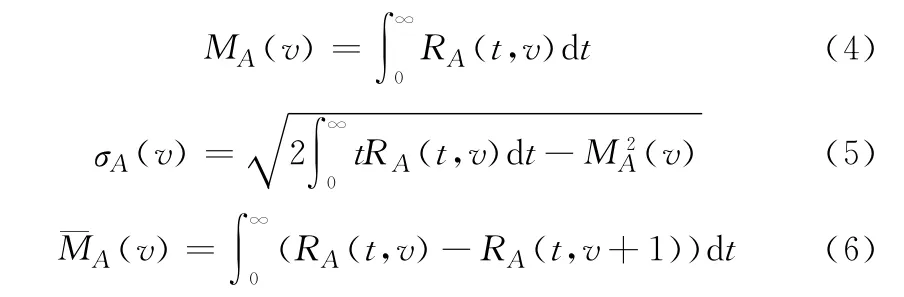
式中:MA(v)为系统A驻留于状态子集{v,v+1,…,s}的平均期望时间;σA(v)为平均期望时间MA(v)的标准方差;(v)为系统A驻留于状态v的平均期望时间。
1.3 元件与系统的耦合关联
元件U ij与系统A间的耦合结构不同,相关状态耦合关系也不同。此处,仅就多状态装备复杂系统可靠性研究中,较具代表性的两类耦合结构,说明如下。
(1)串并耦合结构:
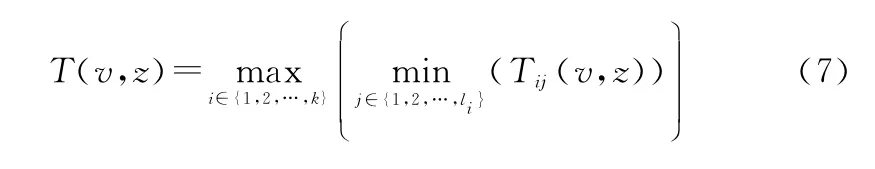
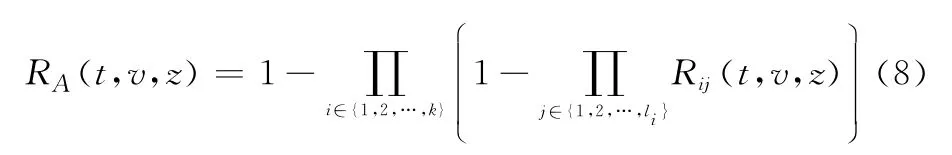
式(7)和式(8)反映了大型串并耦合装备系统z工况下元件与系统之间状态驻留时间和可靠度的耦合关联。现实工程中的大型分布式能源供应系统(如天然气、原油等),多为此类状态耦合结构。
(2)并串耦合结构:
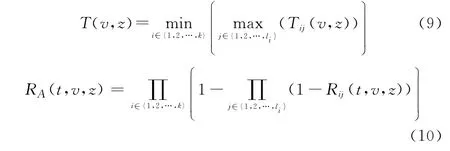
式(9)和式(10)反映了大型并串耦合装备系统z工况下元件与系统之间状态驻留时间和可靠度的耦合关联。现实工程中的大型缆索牵引系统、光纤网络信息传导系统等,多为此类状态耦合结构。
观察前述各式可知,如果直接利用式(8)和式(10),解算评估大型装备复杂系统的多状态可靠性,在已知元件U ij的可靠度函数Rij(t,v,z)前提下,至少还需实施l1×l2×…×l k次乘法运算。对于大型装备复杂系统来说,k与l i的取值通常较大(k>10,l i>10),此时若想实现系统可靠度的精确解算,所需占据的计算机资源往往较多,解算耗费时间也往往较长。本文尝试采用恰当的数学预处理方式,在保证工程逼近精度的前提下,大幅度提升大型装备复杂系统的多状态可靠度求解效率。为此,引入极限序列核的概念。
2 极限序列核
由式(3)易知,系统A的可靠度本质上体现为随机变量T(v,z)的概率分布特征。因此,如果能够通过恰当的数学变换处理,将随机变量T(v,z)的概率分布,映射于某一已知的标准概率分布空间,则可直接利用已知标准概率分布空间的诸多数学特征,反向解算系统A的可靠度。进一步,如果对于任意大型装备复杂系统A,存在序列对〈Φ(n,v,z),Ψ(n,v,z)〉,n∈N,使得式(11)和式(12)同时成立,则称这类与系统A组成结构和元件U ij数目密切相关的序列对为用于解算系统A可靠度的极限序列核。
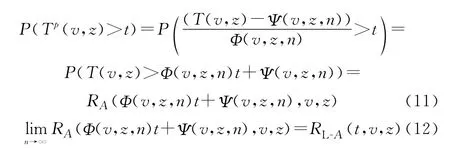
式中:T p(v,z)为经过数学变换预处理后系统A的状态驻留时间随机变量;RL-A(t,v,z)为系统A的极限可靠度函数;n为与k、l i相关的反映系统A总体元件组成的序列数。
继而,如果在函数RL-A(t,v,z)的连续时间点集CR-L-A上,可以找到这样的极限序列核,则当系统A的组成元件个数n足够大时,可近似逼近系统A的可靠度函数R A(t,v,z)如下:
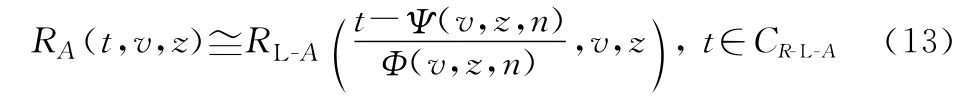
需要说明的是,工程上大型装备复杂系统的结构组成与耦合模式多样,并不一定能够找到符合式(11)和式(12)变换要求的极限序列核。但对于符合齐次和规则特征的大型装备复杂系统而言,通常可以通过恰当的数学手段,找出符合要求的极限序列核,且并不唯一。
3 大型装备系统可靠性快速算法
以符合齐次和规则特征的大型并串耦合结构系统为例,示例说明大型装备复杂系统的极限序列核的确定过程,以及相关多状态可靠性的快速分析与评估算法。如图1所示,某大型装备复杂系统的元件组成与并串耦合结构,符合齐次和规则特征,即对任意i,j取值,均有
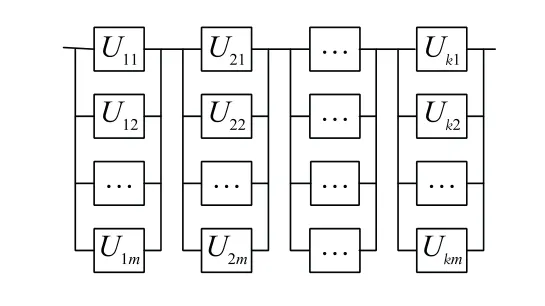
图1 齐次并串耦合规则系统可靠性框图Fig.1 Reliability scheme of a homogeneous parallel-series coupling regular system
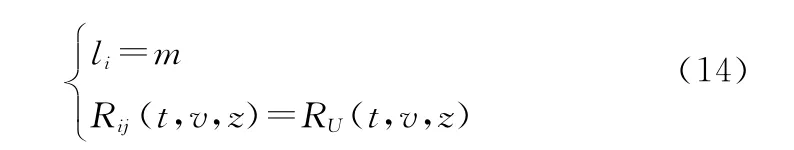
式中:m为齐次规则系统各子系统所包含的元件数;RU(t,v,z)为齐次规则系统各组成元件的多状态可靠度函数。
为便于后续算法结论的演绎说明,给出如下引理。
3.1 算法引理
对于满足齐次和规则约束条件的任意大型并串耦合系统A,取k=n,且存在正整数c1,c2,使得m-c1lnn≫c2成立。
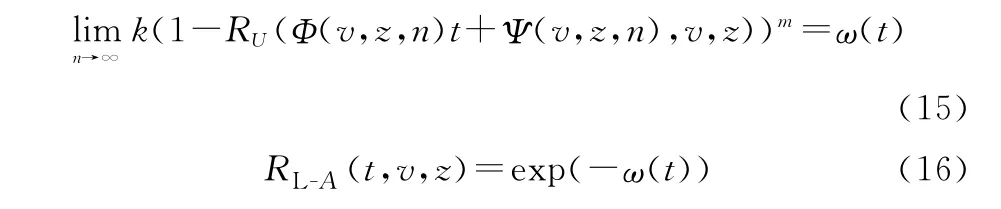
如果其极限序列核〈Φ(n,v,z),Ψ(n,v,z)〉和极限可靠度函数RL-A(t,v,z)存在,当且仅当式(15)给出的序列函数极限存在,且此时系统A的极限可靠度函数RL-A(t,v,z)应具有式(16)所示指数函数表达形式。
上述引理的证明较为繁琐复杂[33-34],此处直接引用结论。
3.2 算法示例
进一步,假设大型并串耦合系统A组成元件的多状态可靠度满足威布尔分布特征[35],即
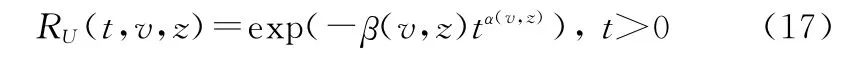
式中:α(v,z)、β(v,z)为与系统工况和元件状态相关的威布尔分布常量。由前述引理,可尝试构建系统A的极限序列核如下:
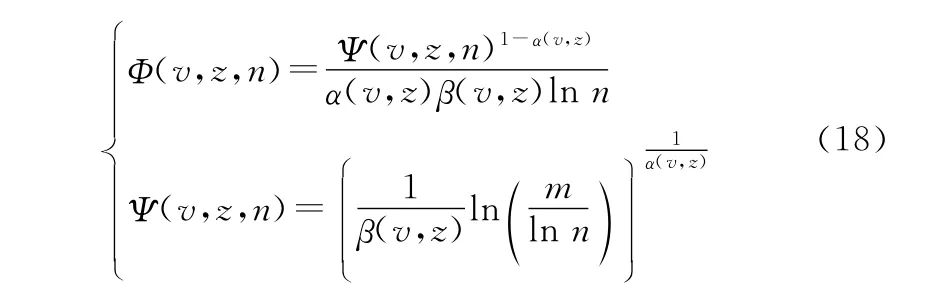
式中:ln(·)为指数底的对数函数。则有
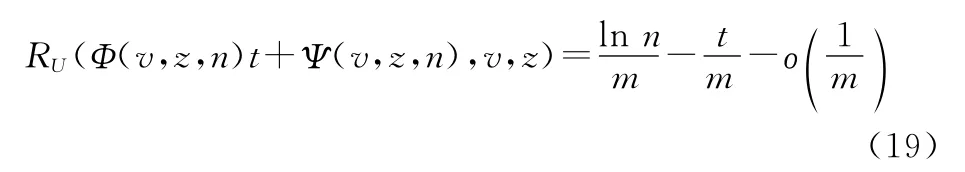
式中:o(·)为高阶无穷小函数。再依据式(15),有
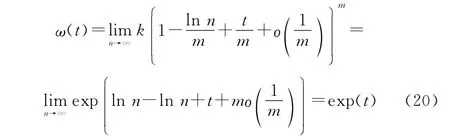
进而,依据式(16),有
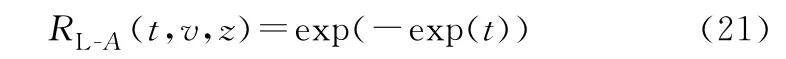
至此,可实现大型并串耦合系统A的多状态可靠性快速分析与评估如下:
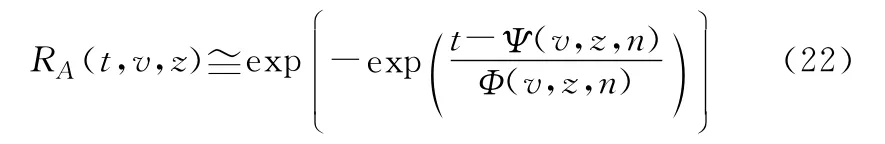
对比式(10)和式(22)的数学表达形式可知,引入极限序列核的快速算法,避开了传统并串耦合系统可靠性解析分析中的大量级叠乘运算,直接利用系统的极限可靠度函数RL-A(t,v,z)逼近原并串耦合系统的多状态可靠性特征,虽在求解问题的技术难度上有所增加,但大大提升了解算问题的工作效率。
4 应用案例
4.1 船用升降转运系统
某船用升降转运系统由传动马达、牵引钢索、载重平台、电控装置4个分系统组成,相关系统可靠性框图如图2所示。鉴于牵引钢索长期暴露于高温、高湿、高盐度、雨水、曝晒、腐蚀等海洋恶劣工作环境,且频繁承受升降载荷的直接冲击,因此船用升降转运系统的可靠性能主要取决于牵引钢索分系统的可靠性能,即。

图2 升降转运系统可靠性框图Fig.2 Reliability scheme of a lifting and transferring system
其中,牵引钢索分系统由12根特种钢索组成,每根钢索的承力状态下降,均会直接导致整个牵引钢索分系统的工作状态下降。每根特种钢索又分别由12根外侧钢缕丝和14根内侧钢缕丝扭绕组成,相关横截面结构如图3所示。升降转运系统工作时,钢索内部的26根钢缕丝同时承受转运载荷的冲击,并呈现并联受力状态。内外侧钢缕丝虽几何尺寸不同,但可靠性能相同,均满足威布尔分布特征[36]。
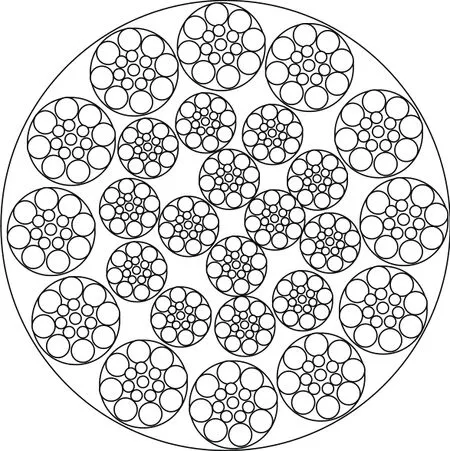
图3 特种钢索横截面结构Fig.3 Cross-section structure of the special steel cable
4.2 系统多状态多工况说明
基于前文关于船用升降转运系统各分系统及组成构件工作特征的阐述,可将其简化为一类齐次规则并串耦合系统(k=12,m=26)。系统(组件)使用过程中,可能遭遇以下不同输出状态与运行工况。
(1)多状态说明
升降转运系统的牵引钢索在海上恶劣环境中长期使用,将会逐渐产生性能退化,呈现4类状态输出水平,如表1所示。
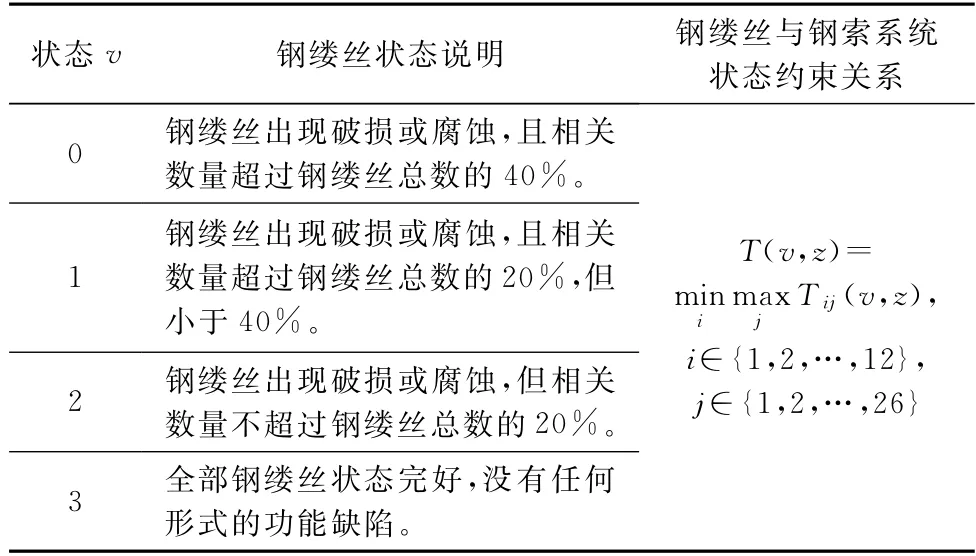
表1 牵引钢索4类状态输出Table 1 Four output states of traction cable
表1中,T ij(v,z)为z工况下钢缕丝自状态3触发,处于{v,v+1,…,3}状态子集的随机驻留时间变量;T(v,z)为牵引钢索分系统处于{v,v+1,…,3}状态子集的随机驻留时间变量。
(2)多工况说明
升降转运系统的牵引对象多样,不同载荷作用下,牵引钢索的可靠性能并不尽一致。依据升降转运系统历次执行任务的年度数据,经承力载荷聚类统计分析,可将其工况分为4类,如图4所示。
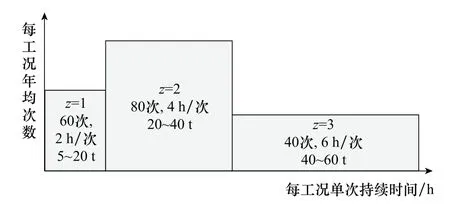
图4 4类工况的年平均分布情况Fig.4 Annual average distribution of four working conditions
图4中,载荷度量单位为t,时间度量单位为h;工况3代表转运载荷处于40~60 t,年均40次,每次任务持续6 h;工况2代表转运载荷处于20~40 t,年均80次,每次任务持续4 h;工况1指转运载荷处于5~20 t,年均60次,每次任务持续2 h。转运载荷小于5 t,或无转运任务,统一视为工况0。由此,可知4类工况在升降转运系统年度使用过程中的发生概率qz,z∈{0,1,2,3},如表2所示。

表2 4类工况的年度发生概率Table 2 Annual probability occurrence of four working conditions
4.3 系统极限序列核解算
参考文献[37]中有关绳索的可靠性数据,以及业内专家的部分实践经验,取单位时间尺度为年,则有钢缕丝的多状态可靠性威布尔分布常量α(v,z)、β(v,z),如表3所示。
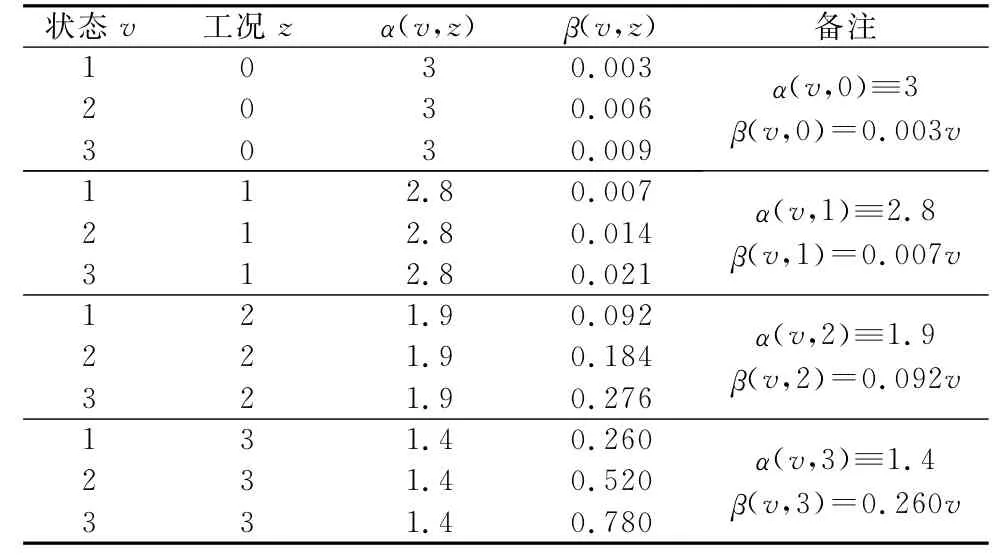
表3 威布尔分布常量α(v,z)、β(v,z)Table 3 Weibull distribution constantsα(v,z)andβ(v,z)
进而,由式(18)可知,升降转运系统4类工况下的多状态极限序列核〈Φ(12,v,z),Ψ(12,v,z)〉如表4所示。

表4 极限序列核〈Φ(12,v,z),Ψ(12,v,z)〉Table 4 Limit sequence kernel〈Φ(12,v,z),Ψ(12,v,z)〉
4.4 系统可靠性评估
进一步,基于式(2)和式(22),以及表2和表4的计算结果,可知升降转运系统的多状态可靠度函数R(t,v)快速逼近表达式:

鉴于篇幅所限,此处仅给出R(t,1)的快速逼近表达式。
进而,基于式(4)~式(6),可知升降转运系统驻留于状态子集{v,v+1,…,s}中的平均期望时间M(v)和平均期望方差σ(v),以及驻留于状态v的平均期望时间ˉM(v)。相关数值解算结果如图5、图6和表5所示。其中,时间t的度量单位y表示年,p(t,v)为系统驻留于状态v的概率。
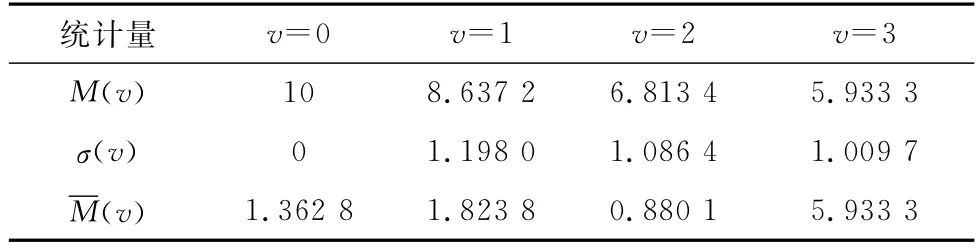
表5 系统状态驻留时间T(v,z)统计特征Table 5 Statistical characteristic of system state dwell time T(v,z)
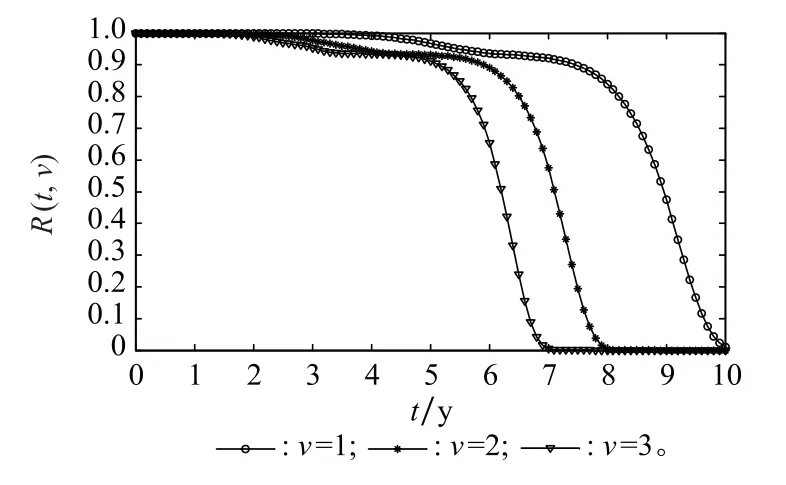
图5 升降转运系统多状态可靠度函数R(t,v)Fig.5 Multi-state reliability function R(t,v)of the lifting and transferring system
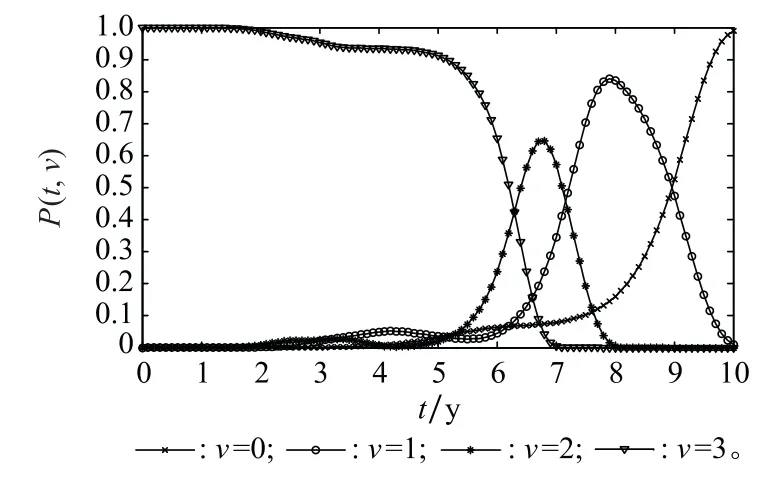
图6 升降转运系统处于不同状态的概率p(t,v)Fig.6 Probability function of the lifting and transferring system in different states
观察图5中的可靠度曲线和图6中的状态概率曲线可知:系统自最优状态触发,随着使用时间的增长,处于状态子集{v,v+1,…,3|v≠0}的可靠度呈现单调下降趋势(不考虑维修);历经约5 y左右时间,系统处于上述各状态子集的可靠度,均会出现迅速衰减,其中可靠度R(t,3)的衰减速度最大;同时,自5 y左右时间起,系统位于最优状态的概率p(t,3)迅速下降,而位于其他劣化状态的概率迅速上升;3~5 y时间阶段,系统牵引功能状态水平逐步趋于劣化,持续运行的安全风险较大,工程技术人员应对这一时间阶段给予充分关注,必要时提前安排相关预防性维修活动。
观察表5中的状态驻留时间T(v,z)统计特征数据可知:10 y使用周期内,系统处于最优状态的期望时间最长,约为5.93 y;若取v=2为系统风险评估的关键辨识状态,则系统处于可接受状态子集{2,3}的期望时间,约为6.81 y;处于不可接受状态子集{0,1}的期望时间,约为3.19 y。进一步,取系统最高可接受的风险门限为r=0.05。
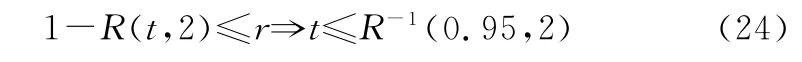
式中:R-1(·)为系统可靠度函数的逆函数;0.95为与风险门限对应的系统最低可接受的可靠度量值。由式(24)可知,为确保系统日常使用中的风险可控、可接受,其持续使用时间t,不应超过3.8 y。
4.5 快速算法效能评估
从解算速度和数值误差两个方面,评估前述极限序列核快速逼近算法的解算效能。
(1)解算速度评估
对于案例所述齐次规则情形,式(10)所示大型并串耦合系统的解析表达式退化为
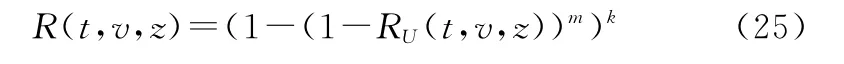
式中:R(t,v,z)、RU(t,v,z)分别为z工况下升降转运系统和钢缕丝处于状态子集{v,v+1,…,3}的可靠度函数。由此,基于式(2),可得系统的多状态可靠度函数R(t,v)的解析表达式如下:
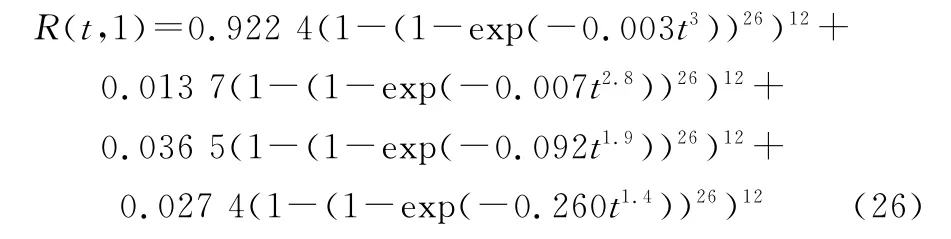
同样,鉴于篇幅所限,此处仅给出R(t,1)的解析表达式。对比式(23)和式(26)可知:式(23)仅需执行两次嵌套形式的指数函数运算,即可完成z工况下系统可靠度函数R(t,v,z)的快速逼近求解;而式(26)则需至少执行312次内含指数函数的多项式乘法运算才能完成。
针对文中案例,采用相同硬件平台Thinkcenter M910t、软件语言Matlab R2014和逻辑编程结构for循环语句,分别基于极限序列核快速逼近算法和直接解析算法,实现转运系统多状态可靠度函数R(t,v)的自动化数值求解。解算步长取0.1,解算时长取10,则完成转运系统全部404个多状态可靠度量值运算的耗时对比情况如表6所示。
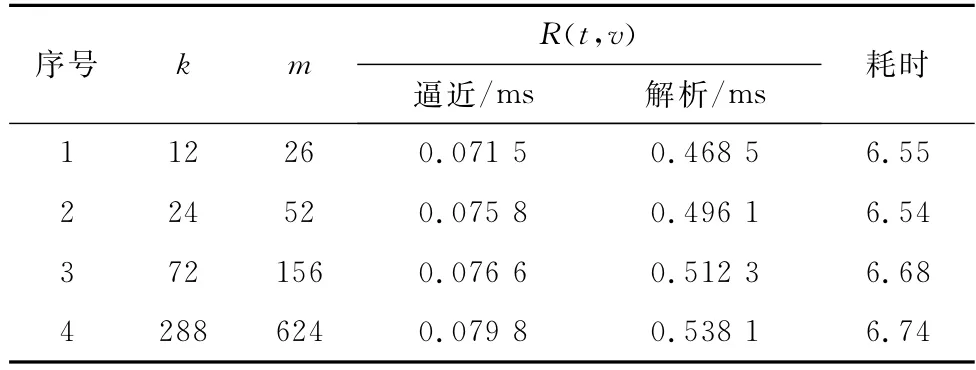
表6 两类算法运算耗时比较Table 6 Comparison of computing time between two algorithms
观察表6中的数据可知:极限序列核快速逼近算法的数值解算速度,约为直接解析算法的6.5~6.7倍,解算速度优势明显;虽然两类算法的解算耗时,均保持在10-2~10-1ms级,但对于可能涵盖大量级类似案例系统的巨型装备复杂系统而言,极限序列核快速逼近算法的应用潜能更为突出。
(2)数值误差评估
图7为分别基于极限序列核快速逼近算法和直接解析算法,数值解算转运系统多状态可靠度函数R(t,v)的曲线对比图。图8为两类算法间的解算数值差函数e(t,v)曲线分析图。
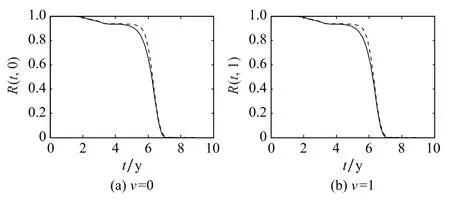
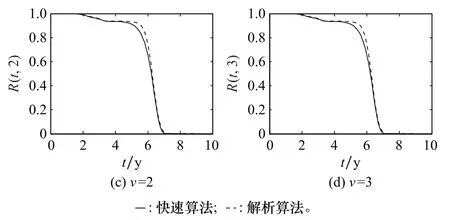
图7 快速算法与解析算法的可靠度解算量值对比Fig.7 Comparison of reliability measures between fast algorithm and analytic algorithm
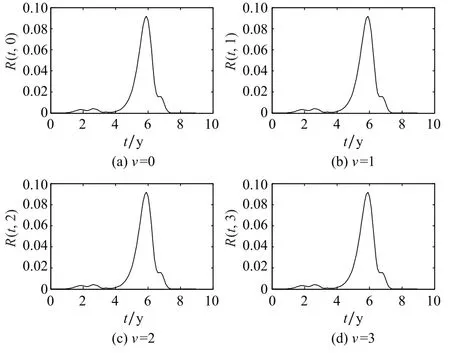
图8 快速算法与解析算法的可靠度解算量值差Fig.8 Difference of reliability measures between fast algorithm and analytic algorithm
观察图7和图8中的曲线可知:极限序列核快速逼近算法与直接解析算法的数值解算结果基本一致,尤其是在0~4 y时间段内,两者数值高度吻合;从10 y总体使用周期来看,极限序列核快速逼近算法给出的系统可靠度量值偏于保守,均小于同时间点的直接解析算法量值;此外,与其他时间段相比,4~7 y时间段内,两者解算的可靠度量值差距较大,峰值可达0.091 8、占比约10%,建议工程应用中,根据实际需求视情修正。
图9为极限序列核快速逼近算法与直接解析算法在风险预报点的可靠度量值差图。由图9可知,临界风险时刻两类算法给出的可靠度量值差仅为0.001 6,与风险预报时间基本吻合。
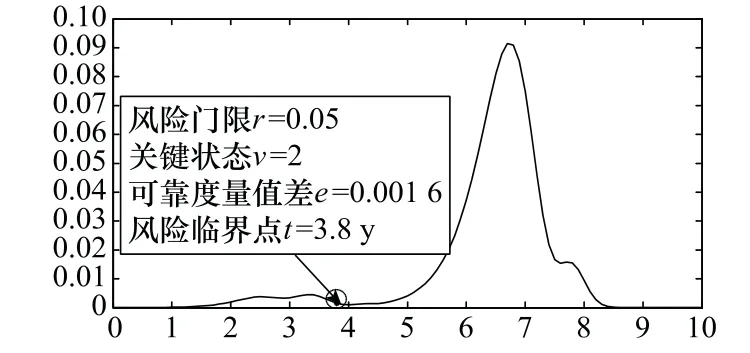
图9 快速算法与解析算法风险预报点的可靠度量值差Fig.9 Difference of reliability measures between fast algorithm and analytic algorithm at risk forecast point
(3)量值差弥补方法
由前述分析可知,基于式(18)明确的极限序列核,解算系统的多状态可靠度函数R(t,v)量值偏于保守。这里,构建另外一类解算结果偏于乐观的极限序列核〈Φg(n,v,z),Ψg(n,v,z)〉如下所示:
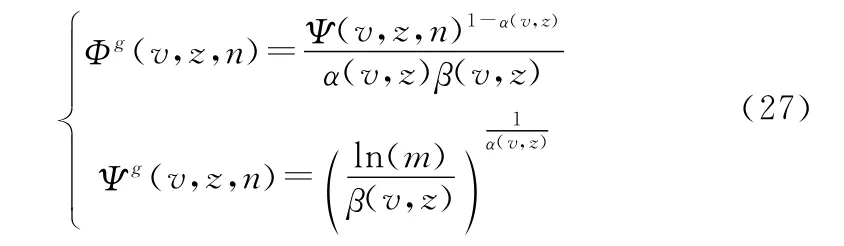
同样,可由下式实现系统多状态可靠度函数R(t,v)的快速逼近:
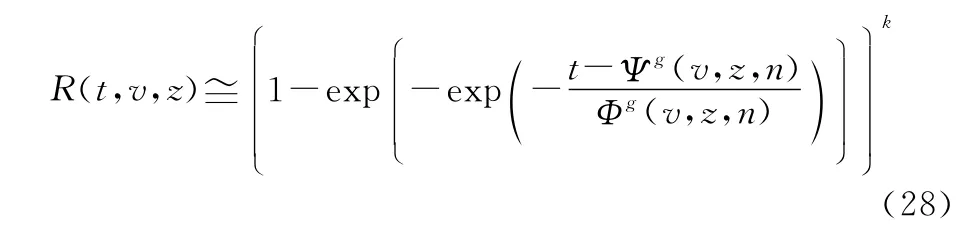
图10为基于两类不同极限序列核,系统多状态可靠度解算量值对比情况。其中,极限序列核〈Φ(n,v,z),Ψ(n,v,z)〉对应快速逼近算法1(基于式(18)确定极限序列核),极限序列核〈Φg(n,v,z),Ψg(n,v,z)〉对应快速逼近算法2(基于式(27)确定极限序列核)。
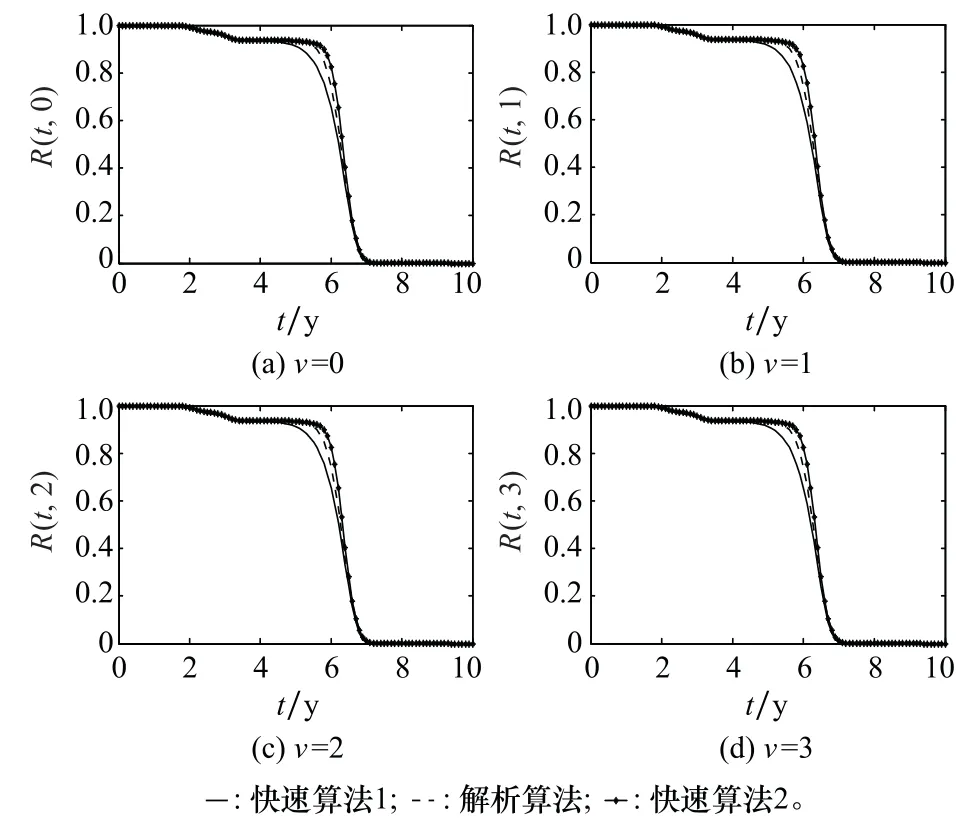
图10 不同极限序列核下系统可靠度解算量值对比Fig.10 Comparison of reliability measures under different limit sequence kernels
由图10可知,两类极限序列核快速逼近算法给出的系统多状态可靠度量值曲线,分别处于解析算法量值曲线的下方与上方。为此,综合两类极限序列核逼近算法,即可有效预测系统多状态可靠度函数R(t,v)的解析值潜在区间,从而合理规避过于耗费计算资源的直接解析运算,并确保所获可靠度解算量值的误差充分可控。
5 结束语
针对工程大型装备复杂系统,通过合理构建面向不同系统耦合结构的极限序列核和极限可靠度函数,探索了一类基于极限序列核的大型装备复杂系统多状态可靠性快速评估算法。研究分析与案例仿真表明:
(1)算法建模合理、解算便捷、评估准确,能有效满足大型装备复杂系统的可靠性评估与风险预报要求;
(2)算法突破了传统解析算法的大维度解算技术瓶颈,大幅度提升了大型装备复杂系统多状态可靠性的评估效率,工程应用潜能大;
(3)算法程式化特征明显,计算资源要求低、计算过程耗时短,便于工程软件的平台开发与核心功能实现;
(4)算法适用范围广,串并、并串、冷储备、表决等常见齐次和非齐次工程耦合结构,均可直接适用;
(5)算法解算弹性大,可满足保守、乐观等不同评估策略下的工程风险管控需求;
(6)算法丰富了复杂系统多状态可靠性建模、分析与评估体系,促进了大型装备复杂系统可靠性快速评估与风险预报技术发展。
下一步工作如下:
(1)探讨非齐次耦合结构下大型装备复杂系统极限序列核构建与极限逼近函数确定的通用方法;
(2)探讨大型装备复杂系统多状态可靠性快速评估交互软件开发内核与工程实现技术。
