具有趋化项和时滞的细菌和病毒疾病传播模型的Turing-Hopf分支

罗湘亿，马淑芳

(东北林业大学)

0 引言

细菌和病毒传播引起的疾病一直是伴随人类世界发展的比较严重的问题之一，比如登革热、HIV、Ebola病毒等等.疾病的出现对人们的生命健康造成了严重的威胁，所以借助数学模型来探究传染病的传播规律，具有重要的指导意义.

传染病斑图是传染病在传播过程中在时间和空间上形成的宏观非均匀规则分布，一些学者对时空斑图的形成进行研究，主要是通过讨论系统的某些高余维分支问题, 像Turing-Hopf 分支、Turing-Turing分支和Bogdanov-Takens分支等[1-6].对这些高余维分支问题的研究，有助于阐明复杂时空斑图的形成机理.

基于上述讨论，该文将研究如下形式的一类具有趋化项和时滞的细菌和病毒疾病传播模型：

其中l是正常数；u(x,t)和v(x,t)分别代表在x点t≥0时的细菌密度和感染人群密度；d1代表细菌的扩散速度；d2代表感染人群的扩散速度；τ为细菌在人类从感染到发病的潜伏期.a11>0是细菌的自然死亡率，a22>0表示感染个体的自然递减率.a12v代表感染性人群对细菌密度的促成作用.非线性项g(u)给出了由于细菌浓度而对人体产生的感染性.▽(ξφ(u)▽v)代表趋化项且φ(u)>0.这里ξ是趋化系数，如果ξ>0(ξ<0)则称为吸引(排斥).生物学上，正趋化系数代表细菌向更高感染人群密度方向移动以增加病毒性疾病传播的趋势.另一方面，负趋化系数代表细菌向更高感染人群密度的相反方向移动以减少病毒性疾病传播的趋势.

该文主要研究模型(1)的正平衡点的稳定性和Turing-Hopf分支的存在性.

1 趋化项和时滞对稳定性和Turing-Hopf分支的影响

为了便于讨论特征值问题，求解了一维有界区域Ω=(0,lπ)(l∈R+).该文假设非线性项g(u)满足：

(H1):g∈C1[0,+∞),g(u*)>0,a11>a22>0,a12>0.

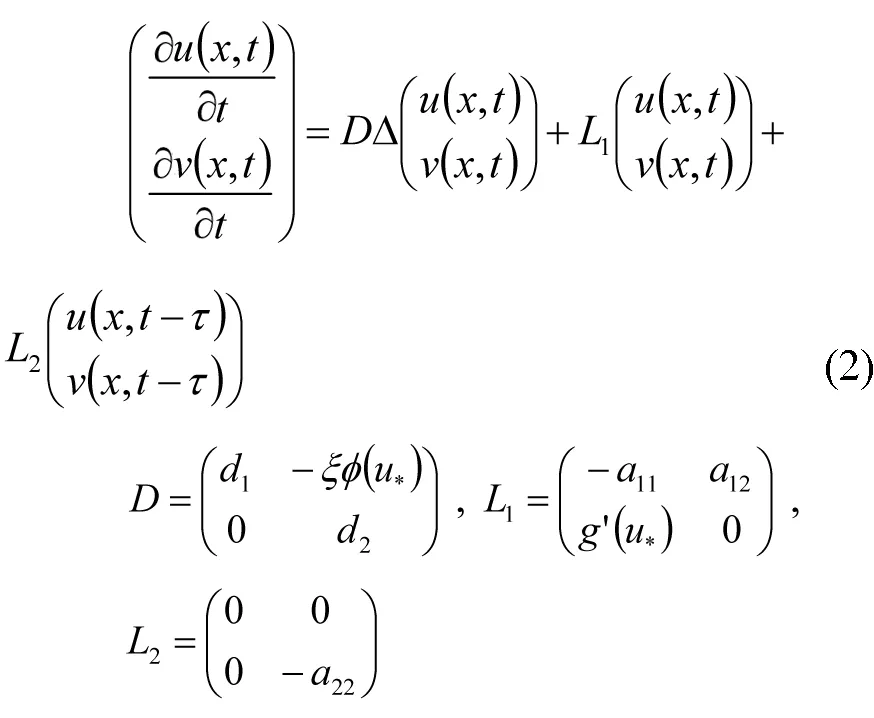
模型(2)的特征方程为：

1.1 Turing分支

该节考虑τ=0时的情形.首先假设：

(H3):a22d1+a11d2<ξφ(u*)g′(u*).

接下来，将讨论模型(1)的正平衡点E*的稳定性和Turing分支的存在性.

从而得出E*是局部渐近稳定的.模型(1)在稳态E*下没有Turing分支和Hopf分支.

当ξ>0时，对任何n∈N0有Mn>0，由(H1)、(H2)、(H3)知存在一些n≥1使Nn<0.也就是说，模型(1)可以发生Turing分支.通过简单的计算，可以得到Turing分支线：

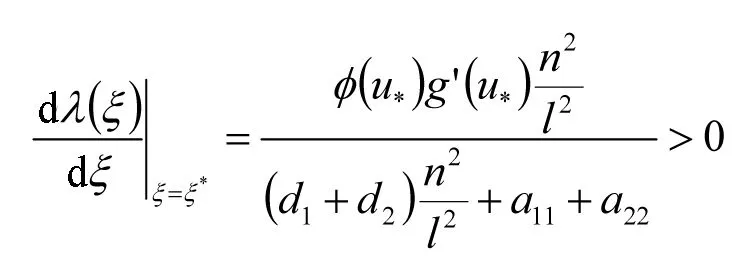
注2 当τ=0时，模型(1)没有Hopf分支，因为对于所有的n∈N0,有Mn(λ,ξ,0)>0.

注3 当τ=0时，趋化项对模型(1)的Turing分支有显著影响，当趋化系数ξ≤0时，模型(1)不存在Turing分支.当ξ>0时，模型(1)在条件(H1)、(H2)、(H3)下可能发生Turing分支.因此，接下来讨论ξ>0时分支的存在性.

基于上述讨论，可得如下定理：

定理1 设(H1)、(H2)、(H3)和τ=0成立.那么：

① 系统(1)的唯一正平衡点E*在ξ<ξ*时是局部渐近稳定的.在ξ>ξ*时是不稳定的(即Turing不稳定).

②对于系统(1)，Turing分支发生在ξ=ξ*>0.

1.2 Bogdanov-Takens分支

当τ>0时，可知λ=0是特征方程(3)的根.当ξ=ξ*时，Δn(0,ξ*,τ)=Nn(λ,ξ*,0)=0.

注4 当τ>0且ξ≤0时，对于任意n≥1，有Δu(0,ξ,τ)=Nn(λ,ξ,0)≠0，故模型(1)没有Turing分支.

根据以上分析，可得如下引理：

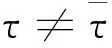
1.3 Hopf分支

接下来，考虑模型(1)的Hopf分支.令：A=

-g′(u*).假设iω(ω>0)是特征方程(3)的一个根.将实部与虚部分离可得：

由于Pn>0，模型(5)有唯一正根当且仅当对于一些n∈N0时Qn<0.为了研究Hopf分支的存在性，给出以下引理来讨论(5)式正根的存在性.

引理2 假设(H1)、(H2)、(H3)成立，定义如下一个集合：

通过模型(4)和引理2，可以计算τ的临界值如下：

由于：

基于以上的讨论，将趋化系数和时滞作为分支参数，给出了如下Turing-Hopf分支存在性的定理.

定理2 假设(H1)、(H2)、(H3)成立，ξ*=ξT(nT)，则有：

①如果ξ<ξ*成立，则模型(1)的唯一正平衡点E*=(u*,v*)在τ∈⎣0,τ*)是局部渐近稳定的，当τ>τ*总是不稳定的.

②对于n∈θ，j∈N0，模型(1)在τ=

τj(n,ξ)处发生Hopf分支.

③对于n∈θ，j∈N0，模型(1)在(ξ,τ)=(ξ*,τj(n,ξ*))处的唯一正平衡点E*附近发生Turing-Hopf分支.

2 数值模拟

在该节中，将通过Matlab进行数值模拟来验证理论结果，所有的数值模拟都采用Neumann边界条件.

2.1 趋化项诱导的空间斑图

选择非线性项g(u)为Ricker形式g(u)=βue-γu[7]，趋化项▽(ξφ(u)▽v)为▽(ξu▽v).因此，可以将模型(1)写为：

令l=1,a11=0.6,a12=0.5,a22=0.4,β=1,γ=1,d1=0.15,d2=2.当τ=0时，描绘了被Turing分支曲线ξ=ξ*在(d1,ξ)参数空间中分隔开的稳定区域和不稳定区域.这表明细菌的扩散速度越快，细菌向更高感染人群密度方向移动以增加病毒性疾病传播的趋势越大.通过简单的计算，得到模型(6)有唯一的正平衡点E*=(0.734,0.8808),ξ*≈18.5241(nT=1)且满足条件(H1)、(H2)、(H3).基于定理1，正平衡点E*如果ξ<ξ*≈18.5241则局部渐近稳定[如图1(a)～(c)和图2(a)所示]，如果ξ=19>ξ*≈18.5241，则不稳定，即Turing不稳定[如图1(d)所示].因此，正平衡点E*在ξ=ξ*附近发生Turing分支.

图1 趋化系数ξ在平衡点E*和初值(u(0,x),v(0,x))=(0.734+0.01cosx,0.8808+0.01cosx)下对模型(1)的影响.(a):ξ=-3;(b):ξ=0;(c):ξ=17;(d):ξ=19.

图2 (a)在(d1,ξ)参数空间中讨论模型(1)动力学的稳定区域.(b)模型(1)的Turing-Hopf分支图

图3 模型(6)的v(x,t)在初始值(u0(x,t),v0(x,t))=(0.734+0.01cosx,0.8808+0.01cosx)的不同参数空间的时空演化(a)区域Ⅰ：E*局部渐近稳定 (b)区域Ⅱ：空间齐次周期振荡 (c)区域Ⅲ：空间斑图 (d)区域Ⅳ：时空斑图

2.2 趋化项和时滞诱导的时空斑图

为了验证由趋化项和时滞的联合影响引起的Turing-Hopf分支，下面研究(ξ,τ)参数空间中Turing分支和Hopf分支的相互作用，如图2(b)所示.在图2(b)中，Turing分支曲线为ξ=ξ*≈18.5241，Hopf分支曲线为τ=τ*≈3.96，点(18.5241, 3.96)为Turing-Hopf分支点.

区域Ⅰ中，从定理2可以得出唯一正平衡点E*局部渐近稳定，模型(1)没有Turing分支和Hopf分支，如图3(a)所示，其中ξ=18,τ=3.7.

区域Ⅱ是纯Hopf分支的区域，意味着E*是不稳定的即Hopf不稳定.空间齐次周期解通过Hopf分支出现在正平衡点E*附近，如图3(b)所示，其中ξ=2,τ=4.

区域Ⅲ是纯Turing分支的区域，这意味着E*是不稳定的即Turing不稳定.非恒定稳态解从Turing分支开始分开，如图3(c)所示，其中ξ=19,τ=3.8.

区域Ⅳ是Turing-Hopf分支的区域，意味着E*是不稳定的，即Turing分支不稳定和Hopf分支不稳定同时发生.模型(6)中Turing分支和Hopf分支的联合影响产生了空间非齐次周期解，如图3(d)所示.其中ξ=18.8,τ=4.

3 结论

该文在Neumann边界条件下，研究了趋化项和时滞相互作用对细菌和病毒疾病传播模型的Turing-Hopf分支的影响.首先，给出趋化项对模型(1)的动力学影响，即负趋化系数(ξ≤0)对唯一正平衡点E*的稳定性没有影响，正趋化系数(ξ>0)能引起模型(1)的Turing分支的发生.接下来，将趋化系数和时滞作为分支参数，得到了Turing-Hopf分支是存在的，最后，通过理论分析和数值模拟表明，在Turing-Hopf分支点附近出现了丰富的时空斑图.对于模型(1)还存在一些有趣的工作.一方面，代替离散延迟，考虑模型(1)的动力学具有非局部时滞或时空时滞.另一方面，可以通过中心流形约简或多尺度分析来推导模型(1)的标准形式，对分支点附近的动力学行为进行分类.