EHB用无刷直流电机齿槽转矩电流补偿控制策略研究

刘金刚，张聪悦，傅兵，孟步敏，胡余良

（1. 湘潭大学 机械工程与力学学院，湖南湘潭 411105；2. 湘潭大学 自动化与电子信息学院，湖南湘潭 411105；3. 佛山市一为制动技术有限公司，广东佛山 528000）

随着汽车电动化和智能化的发展，线控制动成为了汽车制动系统的重要发展方向[1]。线控制动系统主要包括电子液压制动系统（Electro-hydraulic brake system，EHB）和电子机械制动系统（Electromechanical brake system，EMB）。其中，“助力电机+减速增扭机构”形式的EHB可基于现有车载电源系统研制，具有响应快、易于实现再生制动等优点，是目前商业化应用的主流选择[2]。助力电机作为制动系统中液压力的动力源，其性能表现的好坏将决定EHB工作特性的优劣。

无刷直流电机（Brushless DC motor，BLDCM）因具有体积小、质量轻、功率密度高、可靠性高等优点，现已广泛应用在EHB系统上[3]。然而，由于转子永磁体与定子铁心的齿槽相互作用，包括BLDCM在内的齿槽结构永磁电机都会产生齿槽转矩[4]。齿槽转矩的存在将导致转速波动，带来振动和噪声，影响电机伺服系统的控制品质。

就如何降低无刷直流电机的齿槽转矩，当前一直是国内外学者研究热点之一。众多学者从电机本体结构设计优化方面做了大量工作，研究了斜极/槽、槽口宽度优化、不等齿宽、开辅助槽和极弧系数优化等方法。文献[5]以齿槽转矩最小为目标，利用粒子群优化算法对斜极结构进行优化，获得最优参数组合；文献[6-7]研究了不同槽口宽度下的齿槽转矩变化趋势，并选取最优槽口值；文献[8]利用有限元方法分析了调磁块宽度和连接桥厚度对齿槽转矩的影响，给出了优选建议；文献[9]推导了不同齿宽配合情况下的齿槽转矩解析表达式，给出能有效削弱齿槽转矩的齿槽参数确定方法；文献[10]基于有限元法，分析了辅助槽个数、形状和面积等参数对齿槽转矩的影响，获取最优辅助槽结构参数；文献[11]通过不等极弧系数组合削弱齿槽转矩，将全局优化方法与有限元相结合获得最优极弧系数组合。文献[12]提出一种表贴式矩形永磁钢加装凸形极靴的新型磁极结构，大幅减低了齿槽转矩。上述提出的结构优化方法可以有效降低电机的齿槽转矩，但这些方法在实际应用中所需的加工工艺过程繁琐复杂，电机制造难度和成本也相应增加。

为抑制齿槽转矩对助力电机伺服控制品质的影响，本文基于齿槽转矩的变化规律，从控制角度出发，提出了一种利用补偿电流来抵消齿槽转矩的方法，并完成联合仿真验证。该方法无需更改本体结构，能够有效降低BLDCM齿槽转矩的影响，相关研究可为提高无刷直流电机及EHB的综合性能提供参考借鉴。

1 EHB用无刷直流电机模型和齿槽转矩分析

1.1 EHB系统架构及其无刷直流电机模型

某电子液压制动系统的组成架构如图1所示。在ECU的控制下，BLDCM与踏板耦合推动制动主缸活塞，产生主缸压力；主缸液压力经ESP再传输至轮缸，实现车辆制动。BLDCM作为EHB中制动液压力的动力源，其性能表现的好坏将决定EHB工作特性的优劣。

图1 EHB系统组成架构

根据制动系统的设计要求与布局空间限制，某EHB用无刷直流电机的额定功率为300 W，其主要参数设置如表1所示。

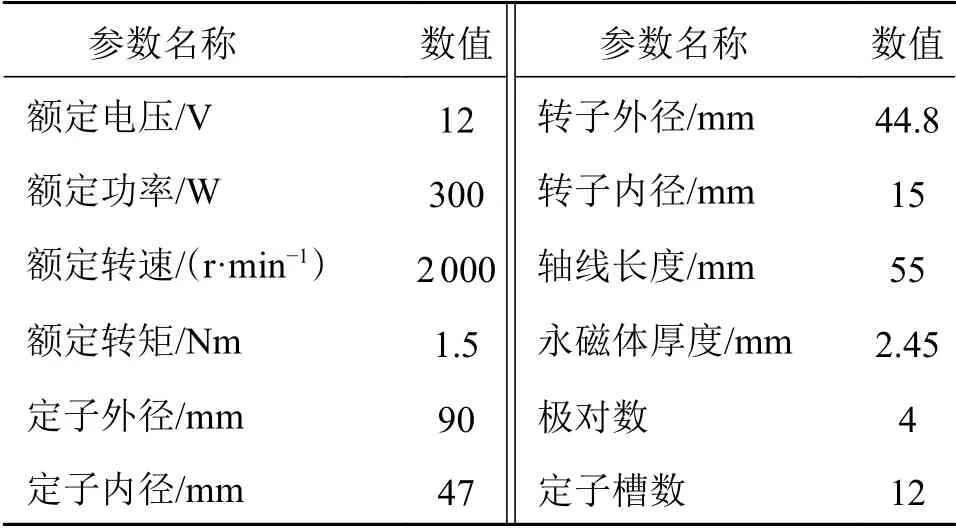
表1 EHB用无刷直流电机主要参数

所采用的BLDCM为分数槽集中绕组，有利于提升槽满率，降低齿槽转矩;转子采用永磁体表贴式结构，结构简单、减少漏磁；定转子采用DW465_50硅钢片叠压而成；考虑到助力电机的高可靠性要求，永磁体选用温度稳定性高、磁性能优异的N30SH。所建立的BLDCM三维模型如图2所示。

图2 无刷直流电机三维模型

1.2 齿槽转矩解析分析

具有齿槽结构的永磁电机旋转时会引起磁场能量变化，进而产生齿槽转矩。该转矩可定义为磁场能量W相对于位置角α 的函数[13]，即

永磁电机磁场中存储的磁场能量可近似为气隙与永磁体磁能之和[14]，表示为

式中：B为气隙磁通密度；μ0为 磁导率；V为气隙体积。其中气隙磁密沿电枢表面分布可表示为

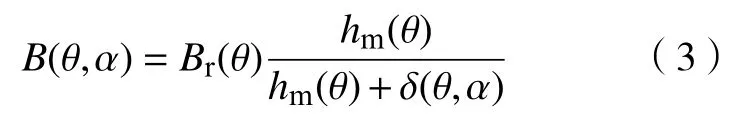
式中：Br(θ)为 永磁体剩磁沿圆周方向的分布；hm(θ)、δ(θ,α)分别为气隙长度沿圆周方向和磁化方向的长度。将式（2）和式（3）代入式（1），进行傅里叶分解展开并求导可得齿槽转矩解析表达式为

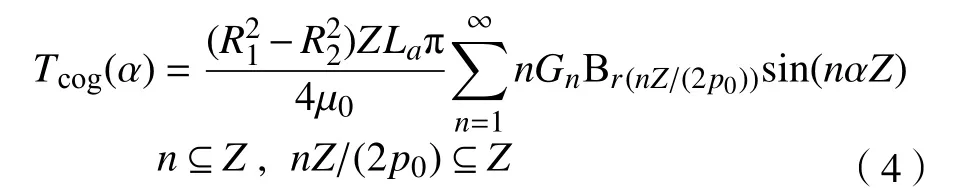
式中：R1、R2分 别为转子外径和定子内径；Z为槽数；La为 铁心长度；Gn和Br(nZ/(2p0))为傅里叶分解所对应n次 和nZ/(2p0)次 谐波系数；p0为极对数。

1.3 齿槽转矩有限元分析

有限元法可以全面考虑电机漏磁、磁饱和等复杂情况，相较于解析法获取的齿槽转矩更为精确[15]。因此，为了准确获取BLDCM的齿槽转矩，使用电磁场仿真分析软件Maxwell建立8极12槽BLDCM有限元分析模型，并对其进行材料定义、边界设置、激励添加和网格剖分。在求解设置中，将电机设置为恒转速工况，绕组电流为零，以永磁体磁场为激励，对该电机进行有限元仿真计算。20 s时刻电机磁感应强度和磁力线分布如图3所示。

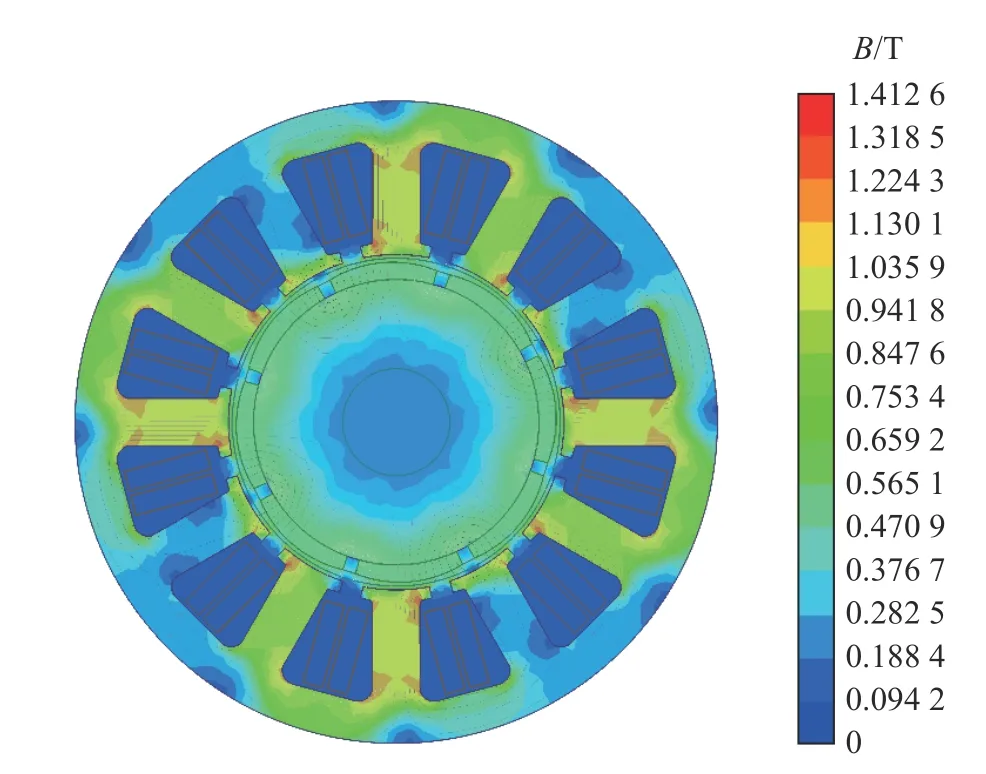
图3 无刷直流电机磁通密度云图

该工况下电机输出转矩就是齿槽效应引起的磁阻力矩，齿槽转矩波形如图4所示。

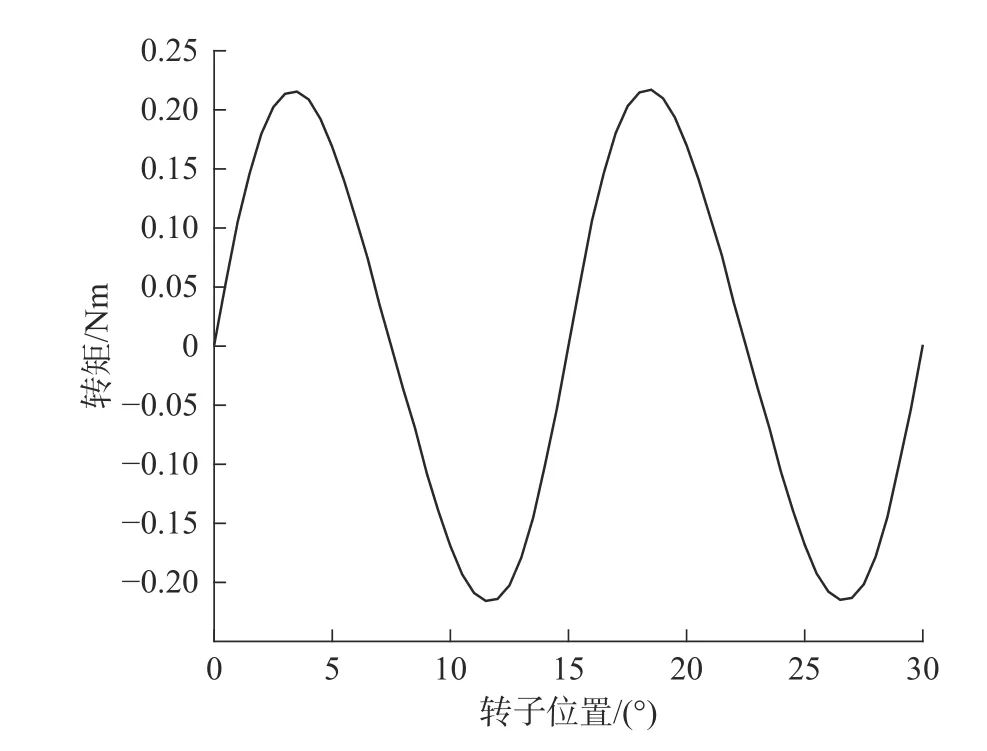
图4 BLDCM齿槽转矩波形图

从图4中可以看出，齿槽转矩是随转子位置变化的周期函数，以转子机械角度15°为一周期，最大值Tcogmax=0. 217 Nm。利用傅里叶级数对齿槽转矩数据进行拟合，得

2 无刷直流电机齿槽转矩电流补偿控制策略

伺服系统中对齿槽转矩要求较高，一般采用正弦波驱动来获得较好的控制性能[16]。矢量控制（Field-oriented control，FOC）具有结构简单、易于实现等优点是常用的永磁电机控制方式之一[17]。在矢量控制中，根据磁动势等效原则通过abc自然坐标系、αβ静止坐标系和dq同步旋转坐标系之间的变换将BLDCM定子电流中的转矩分量、励磁分量进行解耦，达到相互独立控制的目的，获得较好的控制品质[18]。

建立无刷直流电机数学模型时，忽略电机铁心磁阻，不计涡流和磁滞损耗，假设磁场在空间中为正弦分布。BLDCM单元电机的等效物理模型如图5所示。

图5 BLDCM单元电机的等效物理模型

BLDCM电机在dq同步旋转坐标系下的数学模型为：

式中：ud、uq为d、q轴电压；R为定子电阻；id、iq为d、q轴电流；ω为转子角速度；ψd、ψq为d、q轴磁链；Ld、Lq为d、q轴电感；ψf为永磁磁链；Te为电磁转矩；p0为极对数。

从式（8）可以看出，电磁转矩与转矩电流存在线性关系，通过改变电流可以直接控制转矩。因此，根据有限元法获取的齿槽转矩变化规律，在不同转子位置添加对应电流即可对齿槽转矩进行补偿，消除其对电机性能的影响。添加补偿电流后的电机输出转矩表达式为

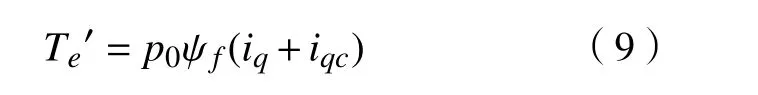
式中iqc为补偿电流。由式（5）和式（8）可得

根据上述思想，基于齿槽转矩的EHB用无刷直流电机电流补偿控制策略的结构框图如图6所示。

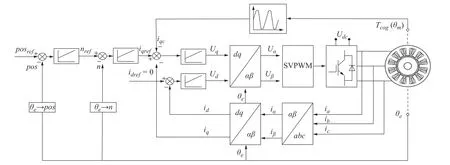
图6 基于齿槽转矩的EHB用无刷直流电机电流补偿控制策略

3 仿真验证

为验证上述电流补偿控制策略的实际效果，利用Simplorer软件建立电机控制模型，利用Maxwell软件建立本体有限元模型，搭建了联合仿真验证平台，从速度伺服与位置伺服两个方面进行仿真对比分析，联合仿真架构如图7所示。

图7 联合仿真架构

某型号EHB用电动助力器的部分参数[19]如表2所示。

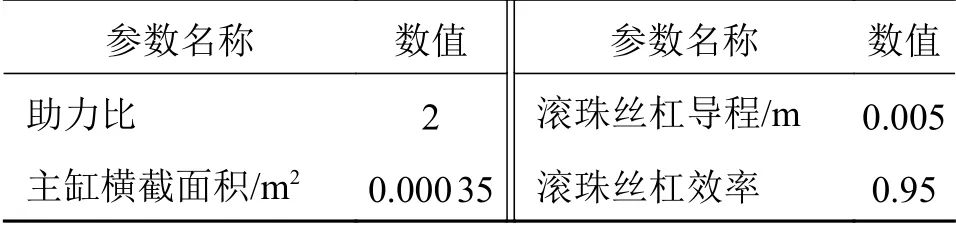
表2 EHB用电动助力器部分参数

电机负载为

式中：T为电机负载；n为助力比；P为制动主缸油压；A为制动主缸横截面积；l为滚珠丝杠导程；η为滚珠丝杠效率。

该型号电动助力器的制动主缸油压区间约为0 ～ 8 MPa，在其范围内选取1 MPa和4 MPa分别代表轻微制动和中等制动两种情况进行分析，由式（11）可得对应电机负载为0.2 Nm和0.8 Nm。

在速度伺服系统中，考虑到主缸活塞行程和响应时间等条件，以目标转速400 r/min、负载0.2 Nm和目标转速600 r/min、负载0.8 Nm为例，分别进行常规速度伺服算法和结合电流补偿控制算法的仿真 分析，结果如图8和图9所示。

图8 电机转速和转矩响应（400 r/min，0.2 Nm）

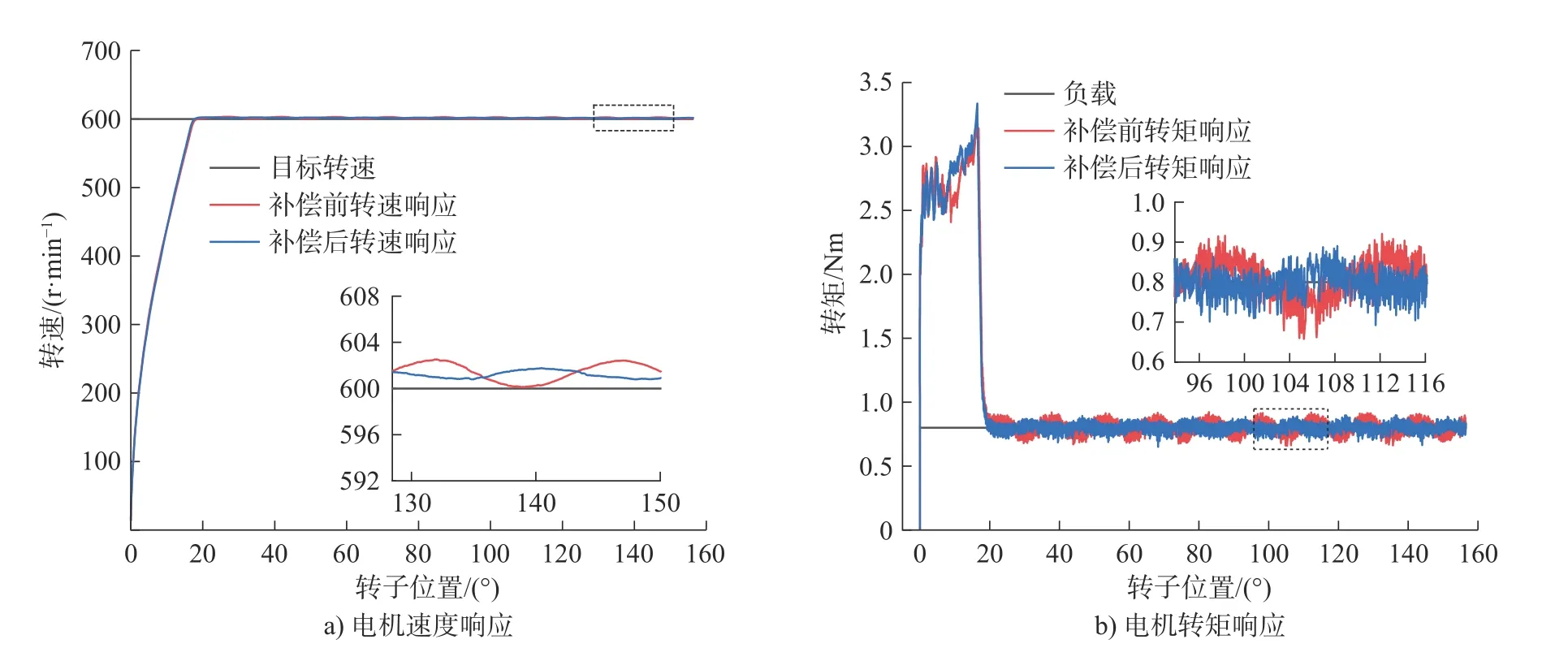
图9 电机转速和转矩响应（600 r/min，0.8 Nm）

未加入电流补偿策略前，目标转速400 r/min、负载0.2 Nm和目标转速600 r/min、负载0.8 Nm在常规速度伺服控制下，电机达到稳态时，转速和转矩随转子位置变化而波动，波动周期与齿槽转矩周期一致，转速波动峰峰值分别达到3.1 r/min和2.61 r/min；加入电流补偿控制策略后，齿槽转矩得到抵消，波动峰峰值分别降低为0.74 r/min和1.16 r/min，较常规速度伺服控制分别减小了76.3%和55.6%，转矩波动明显降低。

转速波动定义为

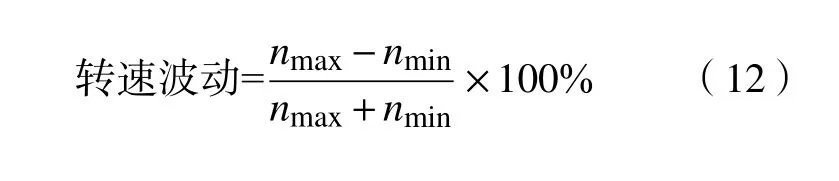
式中：nmax和nmin分别为电机稳态运行时转速的最大值和最小值。相同负载和不同目标转速下，两种控制算法下电机稳态运行的速度波动情况如图10所示。由图10可以看出，电流补偿控制策略可以降低电机转速波动，特别在转速较低时效果更为显著。

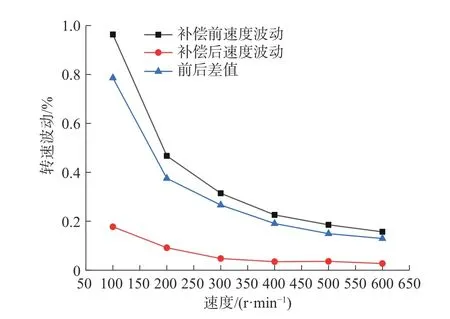
图10 电机转速波动对比

在位置伺服系统中以对应齿槽转矩峰值的目标位置63.75°，负载0.2 Nm和0.8 Nm为例，分别进行常规位置伺服算法和结合电流补偿控制算法的仿真分析，结果如图11所示。

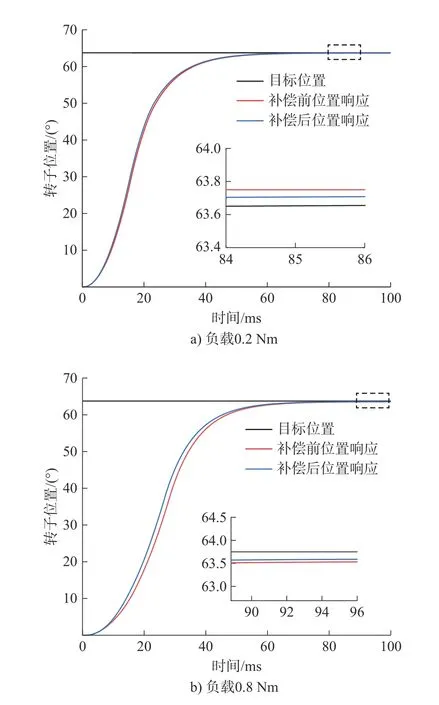
图11 电机位置伺服响应

未加入电流补偿策略前，在常规位置伺服控制下，负载0.2 Nm和负载0.8 Nm的稳态跟踪误差分别为0.08°和0.21°；加入补偿算法后，位置稳态跟踪误差分别降低为0.03°和0.16°，较常规位置伺服控制分别减小了62.5%和23.8%，且伺服响应时间加快。响应时间的缩短主要得益于补偿电流的加入，抵消了齿槽转矩这一附加转矩，缩短了电机输出转矩与负载的平衡时间。

在电机位置伺服系统中随着目标位置的调整，对应位置齿槽转矩的数值将产生变化。为研究齿槽转矩值对位置伺服系统稳态跟踪误差的影响，在Tcog=0 ～ 0.217 Nm范围内均匀设置5个目标位置，负载为0.2 Nm，两种伺服控制算法的仿真结果如图12所示。由图12可以看出，随着目标位置向齿槽转矩峰值接近，稳态跟踪误差逐渐增加，电流补偿策略对伺服控制精度的提升效果也更为显著。

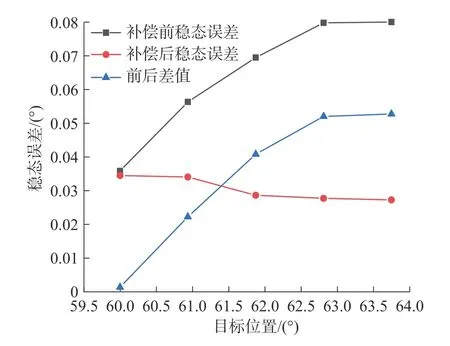
图12 电机稳态误差对比

4 结论

1）基于某EHB用300 W、8极12槽无刷直流电机，建立了其数学模型和有限元模型，并通过有限元法获取了齿槽转矩变化规律。

2）在矢量控制的基础上，基于齿槽转矩与转子位置的映射关系，提出根据电机位置信号对转矩进行实时电流补偿的抑制策略。

3）研究结果表明，结合电流补偿抑制策略的算法与常规伺服控制算法相比，在速度伺服系统中，400 r/min、0.2 Nm和600 r/min、0.8 Nm条件下，转速波动峰峰值分别减小了76.3%和55.6%，转矩波动得到抑制；在位置伺服系统中，63.75°、0.2 Nm和0.8 Nm条件下，稳态跟踪误差分别降低62.5%和23.8%，该策略有效的抑制了齿槽转矩影响，提升了电机伺服系统的控制品质。