考虑柔性车架的无杆飞机牵引系统平顺性研究

祝恒佳 , , ，吕晓 , ，张柏枝 , ，张威 , , ,

（1. 中国民航大学 航空工程学院，天津 300300；2. 中国民航航空地面特种设备研究基地，天津 300300；3. 民航智慧机场理论与系统重点实验室，天津 300300）

飞机离港首先由牵引车将其缓慢推出登机桥 约50 m后，航空发动机点火滑至跑道端头，等待起飞。新一代飞机牵引技术是通过牵引车将飞机以较高速度拉至跑道端头，航空发动机开始点火起飞，从而大幅减少航空发动机工作机时，延长发动机在翼时间。虽然机场道面不平度相对较好，但飞机质量大、牵引车驾驶室与前车轴跨距长，随着牵引速度的提高，长距离、长时间振动产生的较大动载荷对飞机和牵引车结构件的累积疲劳损伤不容忽视；还会影响驾驶员的舒适性，导致驾驶疲劳，增加飞机地面不安全事故风险。因此，研究高速作业时无杆飞机牵引刚柔耦合系统的平顺性对飞机运维保障具有实际工程价值。

目前，国内外学者对飞机地面动力学的研究多为飞机着陆时起落架振动特性分析[1-3]，对飞机-牵引车多体系统牵引过程的动力学研究较少。飞机地面作业速度分为低速（小于11.11 km/h）、中速（11.11～25.93 km/h）和高速（大于25.93 km/h）3类[4]，当前飞机牵引主要具有低速、短距离和重载的特点。

飞机牵引技术包括飞机轮毂电机牵引、有杆牵引和无杆牵引。在飞机轮毂电机牵引研究方面，Roggia等[5]建立轮毂电机驱动飞机机轮的两自由度动力学模型，提出适用于不同牵引工况的电机电压控制策略。但轮毂电机驱动的飞机牵引方式需改变飞机起落架结构，不满足民航飞机的适航要求，且增加了飞机的簧下质量，降低了飞机地面运动平顺性和飞行燃油经济性。在飞机有杆牵引研究方面，陈舒文等[6]建立了有杆牵引系统刚柔耦合动力学模型，对通过加油管地沟时牵引系统可能发生的损伤情况进行了仿真分析；Wang 等[7]针对舰载机牵引系统建立牵引车-牵引杆-飞机系统的虚拟样机模型，利用模糊逻辑理论设计了一种路径跟踪控制器，能有效地实现牵引系统对预定轨迹的跟踪；Schmidt和Alleau[8]对有杆牵引车的牵引过载保护措施开展了相关研究。与有杆飞机牵引车相比，无杆飞机牵引车取消了牵引杆部分，通过车架上抱轮机构将飞机前机轮抱起，使得其体积小、能耗小，牵引速度得到提高[9]。解本铭等[10]建立无杆牵引系统模型时考虑了起落架及牵引车悬架的力学特性，在多工况下仿真得到牵引系统的动力学响应，并对影响牵引系统平顺性的因素进行了优化；王伟等[11]在Adams环境下建立飞机-无杆牵引车动力学模型，分析了无杆牵引车抱轮机构距离车辆重心位置和牵引速度对前起落架振动的影响；杨万辉等[12]采用Adams仿真方法对无杆牵引车转向角阶跃响应等操纵稳定性进行了相关研究，使用阶跃函数模拟了牵引车驾驶员修正转向角的操作；Wang 等[13]建立无杆飞机牵引车的三维车架模型，通过ANSYS Workbench对车架进行有限元静力分析，对原有车架参数进行优化。以上大多数研究主要针对飞机-牵引车系统在低速牵引工况下的准静态力学特性，极少数涉及飞机高速牵引工况下的平顺性研究，且还没有开展飞机牵引车车架柔性对牵引系统振动特性影响的研究。

本文推导了1/2飞机与1/2牵引车模型耦合的无杆飞机牵引系统模型的动力学微分方程，揭示了多工况下无杆飞机牵引刚柔耦合系统的时域振动特性，研究了飞机质量、车架柔性、牵引车质心及座椅位置等多个参数对牵引系统平顺性的影响规律。

1 模型建立

1.1 模型建立

图1为无杆飞机牵引车及其抱轮机构，其特征是车架直接与车轴连接，没有底盘悬架系统进行隔振，且其车架是一种复合式的车架结构，前端车架和梯形车架的形式类似，装有驾驶室与配重件，后端车架为了安装抱轮装置，一般设计成U型结构；座椅距离前车轴跨距较长，较高速行驶时容易造成颠簸加剧，振动问题明显。无杆牵引车通过车架偏后部位的抱轮机构，夹紧抱起飞机前机轮，形成飞机牵引系统，由牵引车提供动力牵引飞机至指定地点，如图2所示。

图1 无杆飞机牵引车

图2 飞机牵引系统

无杆飞机牵引系统属于典型的多体系统，分析其振动特性过程中对模型进行如下简化：

1）牵引车对称于其纵轴线且左右轮胎的路面不平度函数输入相等，所以将牵引车简化为由驾驶室座椅、前后轮胎及车身构成的1/2车模型，其中牵引车车身质量为m1，包括车身车架、车上总成、抱轮机构及前后轮胎，该质量做俯仰运动的转动惯量为J1，前后车轮再经过具有一定弹性和阻尼的轮胎支撑在路面上，座椅簧上质量为m3，包括驾驶员的质量和座椅自身的质量。

2）飞机简化为由机身、前起落架、主起落架及前后机轮的1/2飞机模型，机体质量为m2，该质量做俯仰运动的转动惯量为J2，前起落架簧下质量为m4，包括前起落架部分质量和前机轮集成部件的质量，主起落架簧下质量为m5，包括主起落架部分质量和主机轮集成部件的质量。

3）除起落架缓冲支柱、减震弹簧和阻尼器外其他结构视为刚体，抱轮机构与飞机前机轮固定连接。

4）忽略除机场地面不平度输入外的其他输入，只分析无杆飞机牵引系统的垂向振动。通过对模型的简化，可建立如图3所示的无杆飞机牵引系统动力学模型。

图3 无杆飞机牵引系统动力学模型

图4 为某型号无杆飞机牵引车车架三维图，其前端车架伸出长、跨距大，近似为悬臂梁模型，高速牵引作业时由振动造成的起伏影响不可忽略，将其看作柔性车架；后端车架底盘低、车架较厚，近似为简支梁模型，可以忽略振动的起伏影响，将其看作刚性车架。通过对前端车架的柔性化建模，可以得到无杆飞机牵引刚柔耦合模型（图5），即在图3所示无杆飞机牵引系统动力学模型的基础上，引入前端车架质量m0的垂向运动，z0与F0分别为前端车架质心的垂向位移和垂向受力，得到8自由度无杆飞机牵引系统刚柔耦合动力学模型。无杆飞机牵引刚柔耦合模型的8个自由度分别为牵引车前端车架的垂向运动z0、后端车架的垂向运动z1与俯仰运动θ1、机体的垂向运动z2与俯仰运动θ2、牵引车驾驶室座椅平面垂向运动z3和飞机前后机轮的垂向运动z4、z5，无杆飞机牵引系统的输入为牵引车前后轮上的路面输入激励q1f、q1r与飞机主机轮上的路面输入激励q2。

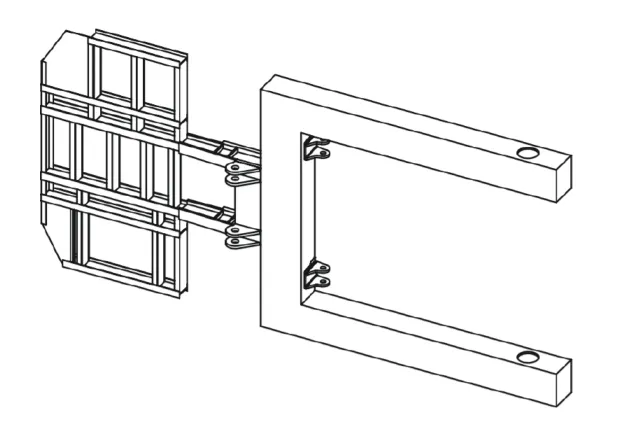
图4 无杆飞机牵引车车架

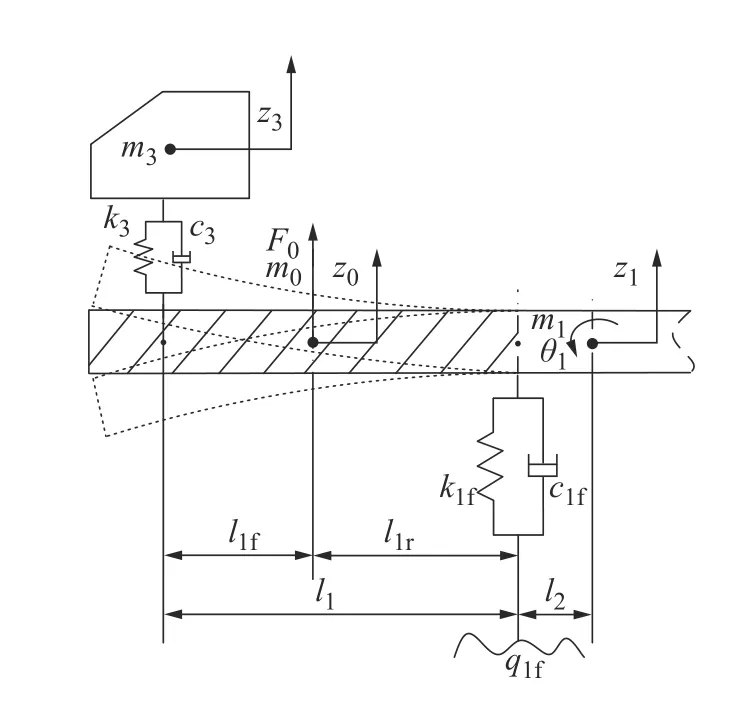
图5 无杆飞机牵引刚柔耦合模型

1.2 模型参数

根据民用航空器牵引标准，目前多数机坪滑行道航空器牵引作业速度最大不超过15 km/h，通常为10 km/h。为了探究新一代飞机牵引技术中高速牵引（40 km/h）对飞机-牵引车系统的动态特性的影响，本文牵引车建模对象以威海广泰AM210作为参考，飞机建模对象为客机机型B737-800，查阅资料可得无杆飞机牵引系统模型参数如表1所示。

表1 无杆飞机牵引系统模型参数

飞机起落架缓冲器多采用油气式缓冲器总的轴向力Fs主要由空气弹簧力、油液阻尼力和内部摩擦力组成，表达式为

空气弹簧力Fa[14-15]公式为

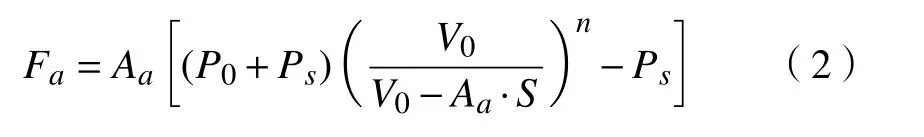
式中：Aa为活塞杆有效面积；P0为空气腔初始压强；Ps为大气压强；S为缓冲行程；V0为空气腔初始容积；n为气体多变指数，油气混合时n=1.1。起落架缓冲器参数如表2所示。

表2 起落架缓冲器参数

油液阻尼力Foil公式为

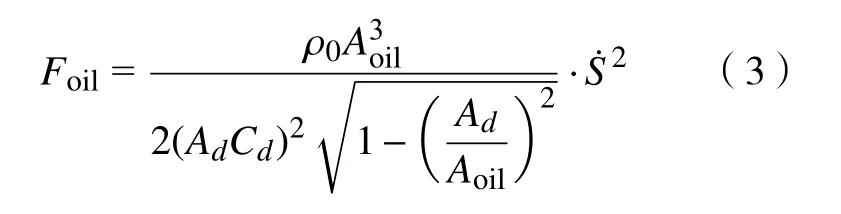
式中：Aoil为活塞杆排挤油液的有效面积；Ad为油孔面积；Cd为油孔卸荷系数；ρ0为油液密度。起落架缓冲器油腔参数如表3所示。

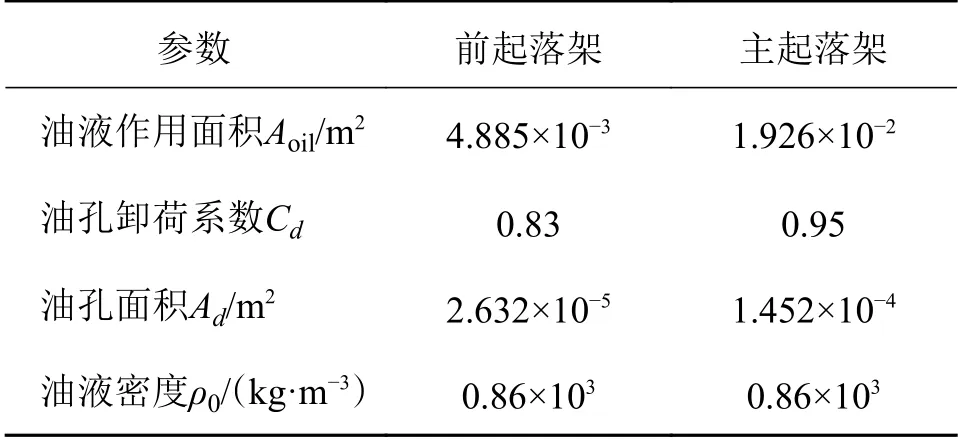
表3 起落架缓冲器油腔参数

内部摩擦力Ff可认为与缓冲器内空气压力成正比，计算公式为

式中：Km为缓冲器皮碗当量摩擦因数，Km=4μphp/D，通常Km取值在0.1 ～ 0.2之间，本文K m= 0.2，μp为缓冲器皮碗与活塞杆间摩擦因数，hp为单个皮碗高度，D为活塞杆直径。对上述公式进行整理可得：

式中：

将KS与CS代入牵引模型中，可得前后起落架缓冲器的等效刚度与阻尼值k2f、c2f、k2r、c2r。

1.3 模型动力学方程

悬臂梁在单载荷下的变形如图6所示。

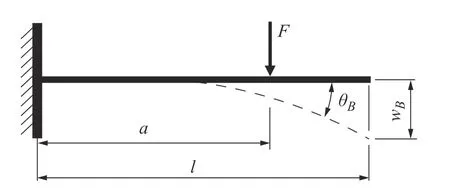
图6 悬臂梁在单载荷下的变形

根据材料力学知识得悬臂梁转角θB与挠度wB公式为：

式中：F为对悬臂梁施加的集中力；a为集中力施加位置与固定端的距离；l为悬臂梁长度；EI为悬臂梁截面弯曲刚度。

前端车架质量为m0，将其近似为悬臂梁模型，车架与前轮连接处看作悬臂梁约束端。引入前端车架截面弯曲刚度EI，w0为前端车架受集中力的垂向变形，通过对上述公式整理得到驾驶室座椅处输入位移w3和前端车架的等效刚度k0的表达式分别为：

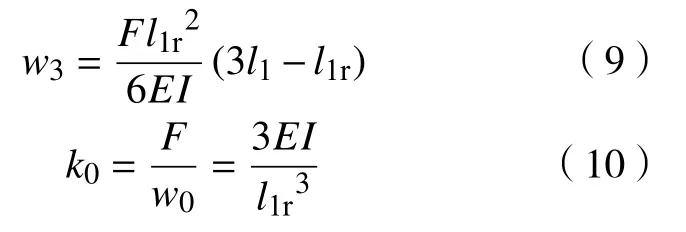
车架截面弯曲刚度EI可通过SolidWorks与Ansys Workbench联合仿真得到，计算公式为

车架模型导入Ansys Workbench中，车架两端固定并施加集中力F= 6000 N，求出该点挠度w=0.0395 mm，将求得参数代入式（11）即可计算出车架的截面弯曲刚度EI= 1.19×105kN·m2，仿真结果如图7所示。

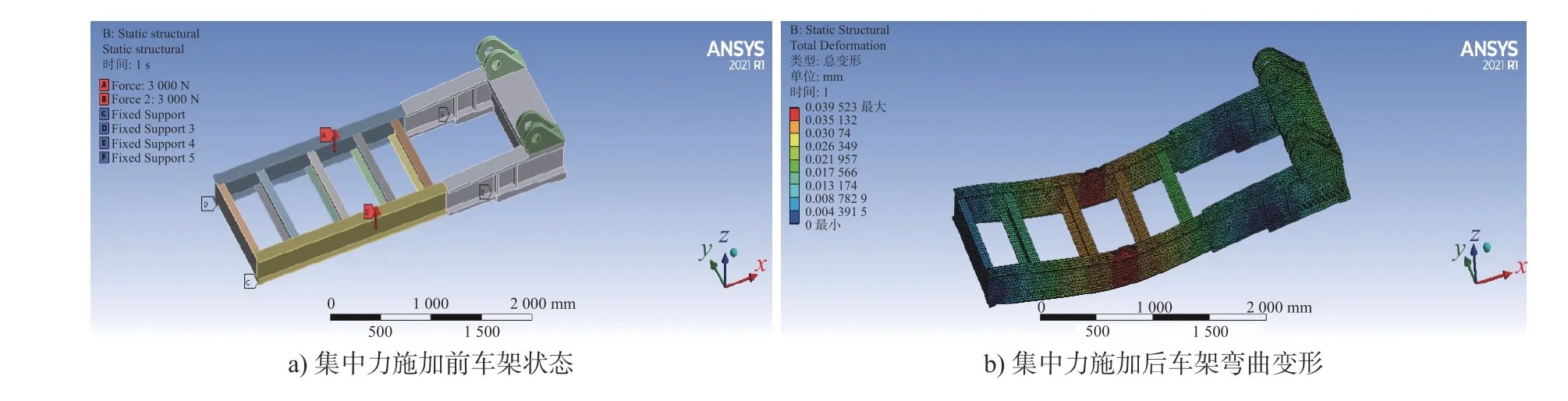
图7 车架截面弯曲刚度计算模型

假设在机场路面激励输入下，飞机牵引系统各部件在其平衡位置附近做小位移运动，由牛顿运动第二定理建立各部件运动方程。

1）车体垂向运动

2）车体俯仰运动

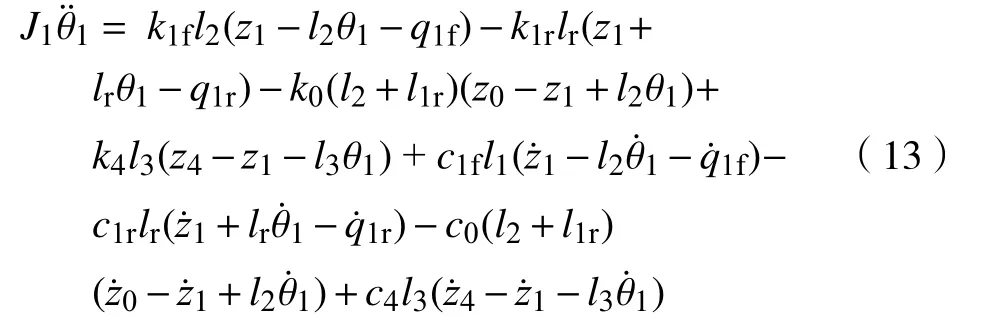
3）机体垂向运动

4）机体俯仰运动

5）座椅垂向运动

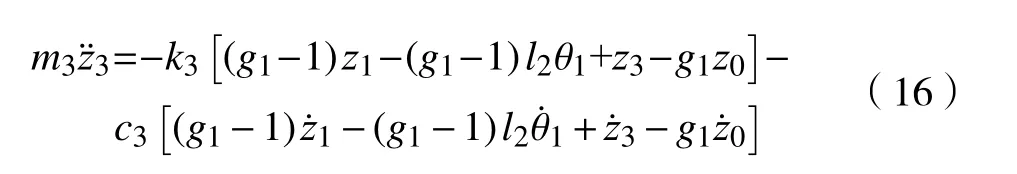
6）飞机前机轮垂向运动

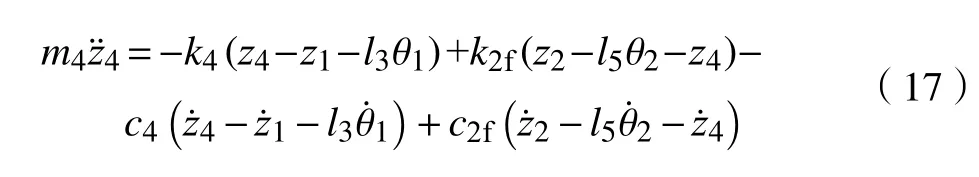
7）飞机主机轮垂向运动

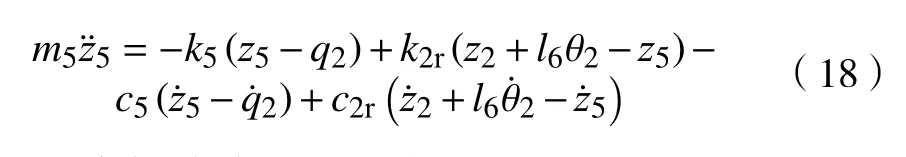
8）车架前端垂向运动

将动力学方程（12）～（19）整理，得到动力学方程矩阵为

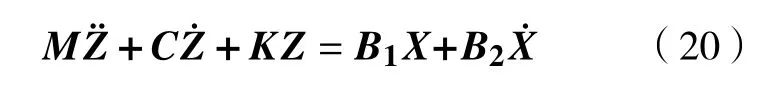
式中：Z=(z1,θ1,z2,θ2,z3,z4,z5,z0)T是系统的运动矩阵；X=(q1f,q1r,q2)T是路面输入激励矩阵；M、C、K分别是牵引系统的质量、阻尼和刚度矩阵；B1、B2分别表示路面位移和速度输入的系数矩阵。

2 牵引系统平顺性分析

2.1 平顺性评价方法

根据《汽车平顺性试验方法》[16]，对飞机牵引系统各关键测点进行平顺性客观评价。脉冲路面输入时，平顺性评价指标为测点最大加速度（绝对值）响应amax；随机路面输入时，对座椅平面加权加速度均方根（Weight root mean square, WRMS）值a¯w、除座椅外其余测点的加速度均方根（ Root mean square,RMS）值aw评价，具体公式如下：

式中：Ga(f)是加速度自功率谱密度函数；fuj、flj分别是频带中心频率的上、下限频率；wj是频带加权系数；a¯j是频带加速度RMS值。

2.2 随机工况输入分析

参考《国际民用航空公约附件14-机场,第Ⅰ卷机场设计和运行》[17]，机场道面不平度需满足用3 m长直尺置于跑道表面任何地方任何方向进行测量时，直尺底面与道面表面间偏差不大于3 mm；结合《机械振动道路路面谱测量数据报告》[18]对路面不平度等级的划分，A级路面不平度均方根值不超过4 mm。对比可知机场跑道路面不平度与A级路面不平度相近，故本文选用A级路面载荷谱作为飞机牵引系统轮胎的输入，牵引速度u分别取10 km/h（低速牵引作业速度）和40 km/h（飞机地面滑行速度）。通过谐波叠加法[19]把机场路面不平度从频域功率谱转化到时域激励q(t)。

空间功率谱密度Gq(n)与时间功率谱密度Gq＞(f)关系式为

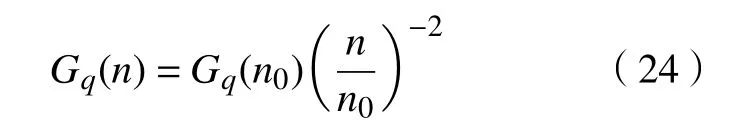
式中：n为空间频率，m-1；n0=0.1 m-1为参考空间频率；f为时间频率，s-1；Gq(n0)为参考空间频率n0下的路面功率谱密度值，A级路面Gq(n0) =1.6×10-6m3。

结合式（24）与巴什瓦等式整理得到路面不平度激励q（t）[20]的表达式为

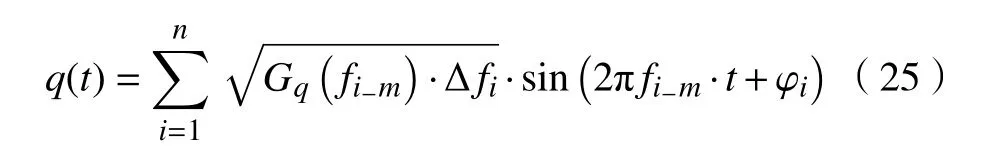
式中：φi为 在 [0,2π]上均匀分布的随机变量；t为牵引滑行时间。

参照《机械振动道路路面谱测量数据报告》[18]，根据谐波叠加法可得到10 km/h与40 km/h速度下机场A级路面不平度和位移功率谱密度，如图8所示。

牵引车前轮与后轮的路面垂向激励q1f、q1r之间存在相位差，与牵引速度及牵引车轴距相关。

图9随机路面工况加速度时域响应，表4为图9所对应的座椅平面垂向加速度WRMS值与RMS值aw、牵引车质心和机体垂向加速度RMS值aw。由图9和表4可知：1）低速与高速牵引作业下，飞机牵引车质心、座椅平面的振动加速度都远比飞机机体大；2）低速牵引作业时座椅平面垂向加速度WRMS值与RMS值 分别 为1.21 m/s2和1.66 m/s2，而高速时分别对应为2.44 m/s2和2.82 m/s2，约为低速结果的202%和170%。在低速与高速两种牵引作业下，与飞机牵引车质心、座椅平面处相比，机体的平顺性都保持良好，主要是由于飞机起落架起到了很重要的隔振作用，而飞机牵引车底盘没有悬架系统，仅通过刚度较大、阻尼较小的轮胎缓冲无法有效消减地面振动。随着飞机牵引速度增大，采用针对传统低速飞机牵引系统的静力学分析方法，已不能准确获取新一代高速飞机牵引系统的动态载荷。

图9 随机路面工况加速度时域响应

表4 加速度均方根值

2.3 脉冲工况输入分析

牵引车在牵引飞机行驶过程中，除去较平坦的A级路面随机激励输入，还可能会遇到勤务井盖、加油管沟盖等凸出地面，即脉冲路面激励输入。某航空公司B737-300飞机由牵引车推出经过加油管造成牵引事故[21]，调查发现该加油管地沟盖与停机坪地面存在约20 mm高度差。

本研究主要考察矩形凸起路面，如图10所示，针对一定的凸起高度（20 mm）、宽度（1500 mm）建立脉冲路面激励模型。

图10 凸起脉冲路面断面示意图

图11 为不同牵引速度下无杆飞机牵引系统在脉冲路面激励工况时的加速度响应对比，表5为图11所对应的座椅平面、牵引车质心和机体垂向运动的amax。总体上随着牵引速度的增大，牵引车与座椅平面垂向运动的最大加速度均增大，而飞机机体垂向运动的最大加速度几乎不变。其中高速牵引时座椅平面处amax最大为19.87 m/s2，约为低速牵引的140%，牵引车质心处amax为13.28 m/s2，约为低速牵引的131%，飞机机体amax为0.15 m/s2，与低速牵引作业基本一致。牵引车及座椅处垂向最大加速度比较大，是因为牵引车仅通过轮胎而没有底盘悬架隔振所导致振动较大，且飞机牵引车和座椅振动都经过较长时间才衰减，说明隔振系统阻尼作用偏小。

图11 脉冲路面工况加速度时域响应

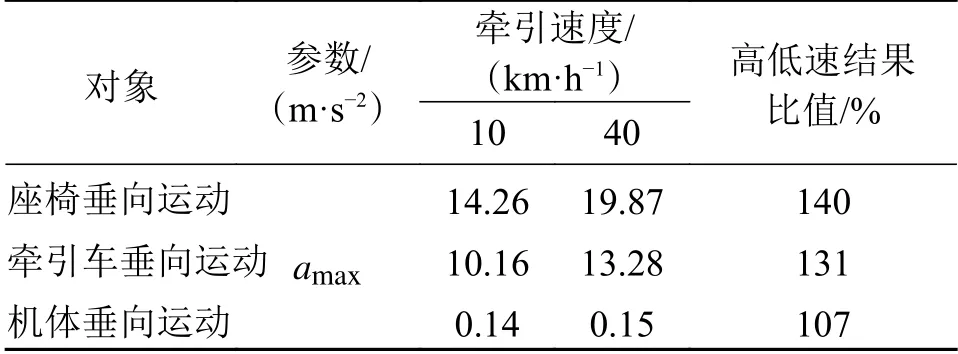
表5 最大加速度值

3 参数影响分析

通过上述两种工况路面输入结果对比分析可知，牵引车座椅平面与牵引车质心处平顺性都较差，且高速牵引时，随机路面工况下牵引系统平顺性变差幅度更加明显。取牵引车垂向运动与座椅平面垂向运动为研究对象，进一步分析牵引系统平顺性受关键参数的影响。

分析随机工况下，40 km/h高速牵引时牵引车质心垂向加速度RMS值aw受飞机质量m2、牵引车车架柔性EI和质心位置l2、l3的影响，具体如表6、表7和表8所示。

表6 飞机质量对车体垂向运动加速度均方根影响

表7 车架弯曲对车体垂向运动加速度均方根影响

表8 牵引车质心位置对车体垂向运动加速度均方根影响

由表6、表7和表8可知：随着飞机质量m2增大，牵引车垂向aw几乎不变，说明飞机机型对牵引车车体垂向运动的平顺性影响很小。改变牵引车车架柔性，随着车架截面弯曲刚度EI的增大牵引车垂向aw逐渐减小，当EI增大到1.7×105kN·m2以上时，继续增大EI值对车体垂向运动的平顺性影响很小，几乎可以忽略；当EI增大到2.5×105kN·m2以上时可将其近似看作刚性车架，与柔性车架结果对比分析，柔性车架牵引车垂向aw约为刚性车架的1.5倍，车架的柔性在一定范围内对车体平顺性的影响结果比较明显。随着牵引车质心位置后移，l2从200 mm增到600 mm、l3从2300 mm减到1900 mm，牵引车垂向aw在l2取400 mm，l3取2100 mm时，车体垂向运动的平顺性最好。

分析随机工况下，40 km/h高速牵引时，牵引车座椅平面垂向运动加速度RMS值aw和加速度WRMS值受飞机质量m2、牵引车车架柔性EI、牵引车座椅位置lf和质心位置l2、l3的影响，具体如表9、表10、表11和表12所示。

表9 座椅平面加权加速度均方根值

表10 车架弯曲刚度对座椅平面加权加速度均方根值的影响

表11 牵引车座椅位置对座椅平面加权加速度均方根值的影响

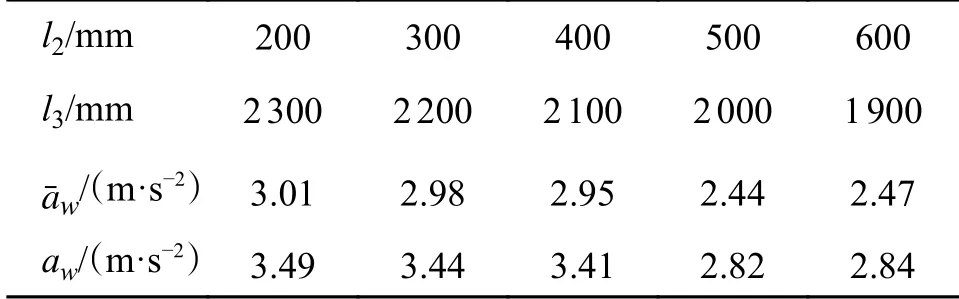
表12 牵引车质心位置对座椅平面加权加速度均方根值的影响

由表9、表10、表11和表12可知：随着飞机质量m2增大，与aw几 乎不变，说明飞机机型对牵引车座椅平面垂向运动的平顺性影响很小；改变牵引车车架柔性，随着车架截面弯曲刚度EI的增大牵引车垂向逐渐减小，但变化不大；随着座椅位置前移，lf从2500 mm增大到4500 mm，从2.40 m/s2增大到2.47 m/s2，变化幅度很小；随着牵引车质心位置的后移，l2从200 mm增大到600 mm、l3从2300 mm减小到1900 mm，座椅垂向在l2= 500 mm，l3= 2000 mm时，座椅平面垂向运动的平顺性最好。

通过上述分析，为改善随机路况下高速牵引作业时牵引车的平顺性、提高牵引车驾驶员的舒适性，车架截面弯曲刚度应适当增大，EI尽可能增大到1.7×105kN·m2以上，车架质心应尽可能靠近后车轴，座椅位置应向车架质心靠近。

4 结论

1） 建立了无杆飞机牵引刚柔耦合系统动力学模型，分析了低速与高速牵引作业时系统各关键运动的随机和脉冲振动响应。结果表明：随着牵引速度增大，由于飞机牵引系统没有悬架弹簧与阻尼隔振系统，其振动加速度RMS值和最大值分别是低速的1.7 ～ 2.7倍、1 ～ 1.4倍，针对传统低速飞机牵引的准静态力学分析方法无法精确获的高速飞机牵引动力学特性。

2） 进一步研究了系统关键参数对无杆飞机牵引刚柔耦合系统平顺性的影响规律。结果表明：飞机质量对系统振动几乎没有影响，适当改变牵引车车架柔性、座椅位置和质心位置可以改善牵引系统的平顺性，其中车架柔性在一定范围内对车体平顺性的影响结果比较明显。为进一步提高牵引系统的平顺性，应考虑加入牵引车悬架系统进行隔振。

3） 通过时域振动分析方法研究了无杆飞机牵引刚柔耦合系统振动的基本问题。