标签分割的软件定义飞行自组网控制器智能部署方法

付有斌，康巧燕，王建峰，胡海岩，赵 朔，3

（1.空军工程大学信息与导航学院，陕西 西安 710077；2.中国人民解放军93107部队，辽宁 沈阳 110042；3.中国人民解放军93303部队，辽宁 沈阳 110042）

0 引 言

软件定义网络是美国斯坦福大学Clean Slate研究组提出的一种集中控制的新型网络架构，其核心理念是将网络设备的控制层与数据转发层分离，由控制层上的控制器对网络资源进行统一调配，对网络实行集中管控，而数据转发层的设备只负责转发数据分组。将软件定义网络的思想引入无人机飞行自组网中，能够有效解决飞行自组网（flying ad-hoc network，FANET）架构僵化、网络资源分配不均、网络效率低的问题，构成软件定义FANET（software defined FANET，SD-FANET）。

最简单的软件定义网络（software defined network，SDN）架构是利用单个控制器对网络中所有的节点进行统一管控，但在FANET中，终端节点的分布范围广，网络规模随任务多样化而不断扩大，单控制器下的网络容易出现单点故障、处理容量有限等问题。基于此，研究者提出逻辑集中、物理分布的多控制器架构体系，随之而来的就是网络的多控制器部署问题。多控制器部署问题（controller placement problem，CPP）主要包括3方面：确定控制器数量、控制器与传输节点的映射关系和最佳控制器部署位置。

Heller等人首次提出CPP，随着研究深入，CPP已经被证明是一个NP（non-deterministic polynomial）难问题，其通用求解思路是根据实际问题需求，确定优化目标并得出优化函数，然后对网络进行划分以缩小搜索范围，最后利用搜索算法寻找可行解。

为解决CPP，近年来有大量的部署策略被研究者提出。首次解决CPP的部署策略指出，控制器的最佳部署位置取决于交换机和控制器的传播时延，并使用贪心算法进行求解，但该算法没有考虑控制器容量的影响。文献［11］采用一种新的迭代和温和匹配条件求解CPP，在考虑控制器容量的前提下不仅能够获得最低的时延，同时实现了最低的执行时间以及更高的内存消耗效率。许多研究都采用聚类算法作为基础解决CPP，如Yao等人提出了一种容量k-center算法，该算法考虑了控制器容量对网络成本和网络效率的影响，根据节点距离进行聚类，同时设定聚类中心作为控制器部署位置，有效减少了控制器数量，简化了网络结构。文献［13］采用改进的k-means算法解决CPP，该算法有效避免了k-means算法结果随机的缺点，但其只考虑平均控制时延，并未考虑负载均衡和跨域通信问题。文献［14］同样是基于k-means算法提出了一种改进型的多控制器部署算法，该算法能够有效降低网络的最大时延，但由于其只考虑单一指标，难以适应复杂网络。k-means算法及其改进算法大都考虑的是最小化时延，没有考虑到控制器容量和部署成本的问题，因此并不是通用的部署算法。而文献［15］以谱聚类算法为基础，引入时延和控制器容量约束进行控制器部署，该算法能够在保证时延约束的条件下使各控制器负载保持均衡；但该算法只能保证时延在约束内，无法保证时延最低，同时也没有考虑部署成本的问题。文献［16］在给定的时延约束下，权衡控制器负载和切换频率，在混合整数线性规划模型的基础上，给出CPP的求解公式，通过Pareto最优算法的求解结果能够满足时延和控制器时延等目标。此外，研究者将启发式算法如蚁群算法、粒子群算法、布谷鸟算法等都被应用到求解CPP，得到的结果都可被认为是较优解，如Fan等人在考虑链路失效的情况下，提出以最小化控制器与交换机之间的时延为目标的部署策略，在该策略中引入粒子群算法进行控制器位置的部署，该算法在80%以上的网络中都能保证网络时延低于10 ms。为了最大化网络链路连通性，文献［22］提出survivor模型，其目标为优化控制器与其每一个传输节点的不相交链路数量，该模型选择不相交链路最多的节点作为控制器部署位置以增强网络可靠性。文献［23］考虑链路故障对网络可靠性的影响，提出一种基于控制时延可靠性的控制性部署算法，该算法基于链路故障定义部署方案可靠性指标，并以该指标最大为准则选择控制器部署方案。

综上可知，现有控制器部署方法大部分都是以优化网络指标为目的，从而完成控制器部署，如优化网络时延、网络可靠性等，除此之外还有综合考虑多个指标的控制器部署算法。但是，当前并没有综合考虑网络时延、控制器容量约束和部署成本三者的算法。基于此，本文提出一种标签分割（label segmentation，LS）的控制器部署方法，首先根据网络中节点状态和约束条件自适应对网络进行划分，保证网络可靠性的同时降低部署成本；然后在此基础上综合考虑平均控制时延、控制域时延波动和控制器负载差异度3个指标，搜索最佳部署方案，从而完成整个部署过程。本文的主要贡献在于：①提出基于LS的控制域划分方法，该方法优势在于能够根据节点的自身特征和关联特征定义惩罚函数，以惩罚函数值最小为准则得出最佳划分结果；同时采用布谷鸟搜索（Cuckoo search，CS）算法对其进行优化，保证输出最优结果的同时降低算法的计算复杂度和收敛时间；②重新定义控制器负载差异度，在考虑传输节点数量的基础上进一步考虑每个节点的流量请求，使其能更加全面地表征控制器负载的差异程度，并通过优化该指标均衡控制器负载。最后通过采用基于改进惯性权重粒子群优化（particle swarm optimization with improved inertial weight，PSO-IIW）算法的控制器部署算法完成整个网络的多控制器部署。

1 模型构建

在SD-FANET中，网络节点的运动范围广、分布稀疏，仅使用一个控制器难以对全网节点进行有效控制，而且当控制器故障或者处理能力有限时，容易引起网络效率下降甚至网络失效等问题。因此，SD-FANET采用分布式的SDN架构，如图1所示。

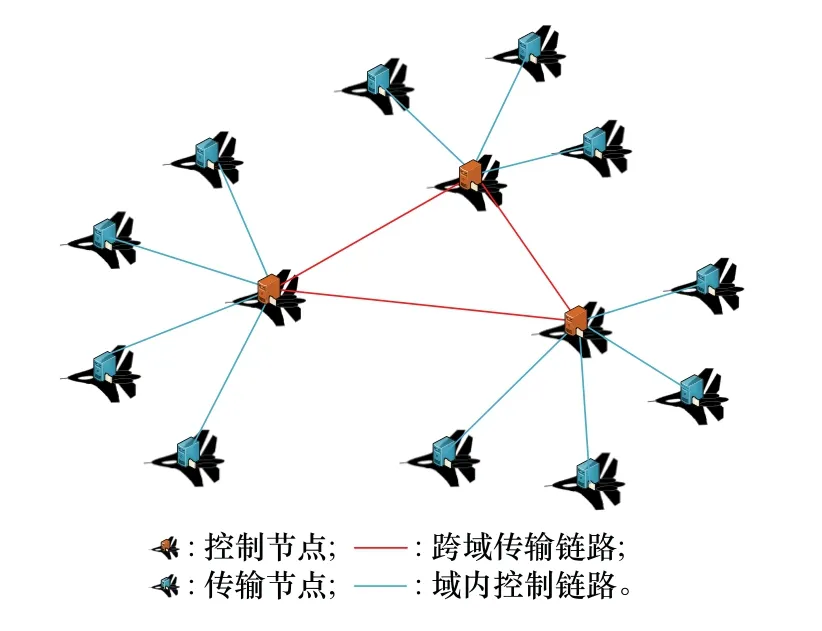
图1 分布式网络架构Fig.1 Distributed network architecture

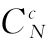
控制器容量：单台控制器的载荷及其处理能力都是有限的，为了使得控制器能够正常工作，需要保证每台控制器管理的传输节点数不超过给定的上限值，该值即为控制器容量。

部署成本：将控制器部署在传输节点的位置，部署成本为所有控制器的成本之和。为了简化起见，假设网络中使用的控制器均为同一类型，部署一台控制器的成本为，则部署成本为

在部署控制器的过程中，控制器数量过多会造成冗余，同时增加不必要的部署成本；而数量过少会导致部分传输节点不受控制器管理或者部分控制器过载的情况，因此在部署控制器之前无法事先确定控制器数量。本文解决的问题可描述为在给定控制器容量下，以最低的部署成本获取最优的控制器部署方案，数学描述为

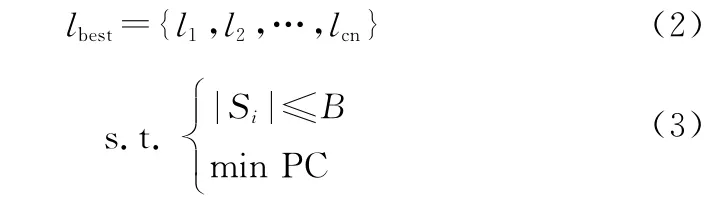
式（2）中的l 表示第个控制器部署节点；式（3）为约束条件，其中S表示第个控制域，｜S｜表示第个控制域中的节点数量。

在多控制器SDN环境下，控制器的部署往往分为3个阶段：控制器数量的确定；根据控制器数量划分控制域；在各个控制域中部署控制器。本文将确定控制器数量和划分控制域合并为一个步骤，在划分控制域的过程中综合考虑部署成本和网络可靠性，自适应地确定控制器数量，然后在已划分好的控制域内部署控制器。因此，可以将多CPP分解成控制域划分和控制器部署两个子问题，根据子问题性质和特点分别解决。

2 控制器部署方法

2.1 基于LS的控制域划分方法

对网络进行控制域划分，其本质就是根据网络中的节点特征对节点进行分类。本文采用LS算法完成控制域的划分。

2.1.1 LS算法

GC（GraphCut）算法是一种图像分割算法，其基本思想是根据图像中每个点的像素值将图像的前景和背景分割开。与谱聚类算法和k-means及其改进算法相比，GC算法能够同时兼顾节点自身属性特征和网络连接性，并根据网络拓扑结构对二者进行均衡从而得到更好的分类结果，因此，本文以GC算法为基础进行改进并提出LS算法。

在LS算法中，每个节点有一个“像素值”，本文称其为节点标签l （l ＝0，1），根据节点标签将节点分为两类，通过重复使用LS算法对网络进行控制域划分，直至结果满足约束条件时结束划分。

节点权值：节点权值是定义自身特征的基础。在网络初始化阶段，所有节点的初始能量、带宽等属性都是相同的，因此将节点权值定义为关于节点时延的函数，其计算公式为

式中：TL 为节点v 与其所有邻居节点间时延的最大值。节点v 和节点v 之间的距离为d ，电磁波传播速度为，节点v 的邻居节点集合为N ，则TL 的计算公式为

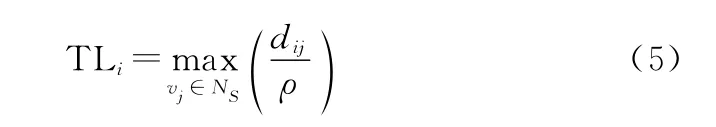
节点标签概率（l ＝l ）：在对节点进行分类之前，对于每个节点都可根据其权值计算出其初始标签的概率，因此可将节点标签概率视为节点的自身特征。在LS算法中，若节点v的权值最大，则令其标签l ＝1，该节点的标签概率可表示为（l ＝1）＝1或（l ＝0）＝0，同理可得权值最小的节点标签概率可表示为（l ＝0）＝1或（l ＝1）＝0。在此基础上，可得其他节点的标签概率计算方法如下：

关联特征AC：关联特征是指节点与网络中其他节点的关联程度，对于网络划分而言，期望将关联程度高的节点归为一类，节点的关联程度与节点间的距离和节点权值有关，节点间距离越小，关联程度越高；节点权值越相近，关联程度越高。因此，定义节点的关联特征函数为

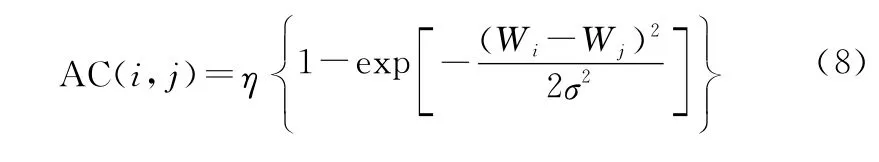
式中：是距离系数，其计算公式为

其中，Rt为节点通信范围。

综合节点自身特征和关联特征，设定一个分类方案的惩罚函数LF，以惩罚函数值最低为准则对网络中的节点进行分类，从而确定最佳分类方案，可表示为

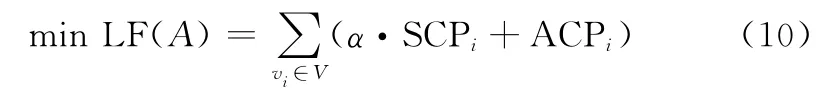
式中：LF（）为该方法下的惩罚函数，为节点分类方法；SCP 为自身特征惩罚函数；ACP 为关联特征惩罚函数；为SCP 和ACP 之间的重要因子，决定其对惩罚函数的影响大小。惩罚函数LF（）值最低时对应的为最佳分类方法。下面给出SCP 和ACP 的定义。

自身特征惩罚函数SCP ：若只考虑节点自身特征，即只根据节点标签概率（l ＝l ）对节点进行分类，此时希望得到的惩罚函数值最小，所以可以将节点v的自身特征惩罚函数定义为

关联特征惩罚函数ACP ：为了使得分类结果更可靠，可在考虑节点自身特征的基础上，兼顾节点的关联特征。在分类方案中，节点的关联程度越高，其对应的惩罚函数值越低。定义节点v 的关联特征惩罚函数为

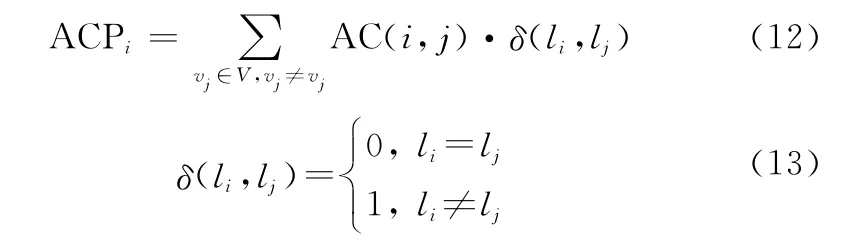
基于LS算法的控制域划分算法用于在给定控制器容量时，如何在约束内得到最佳的网络划分方案＝｛S｝，＝1，2，…，，伪代码如算法1所示。

算法1中第7行中给定参数的取值范围，是为了使得网络划分的结果能够满足组网要求的最少节点数量，在实际应用中可根据组网相关要求设定参数。

2.1.2 LS算法优化

在算法1中，第7～17行是根据惩罚函数最小准则求解最佳分类方案，采取的是穷尽搜索的方式，其优势在于能够通过遍历所有的解从而搜索到最优解，但是计算量庞大，计算复杂度很高。为了在保证能够搜索到较优解的前提下降低计算复杂度，本文采用CS算法对LS算法进行优化。

CS算法是一种新型元启发式搜索算法，其主要优点是参数少、随机搜索路径优、寻优能力强等。在CS算法的搜索过程中，两个位置的更新至关重要。

一个是采用Lévy飞行更新位置，Lévy飞行已被应用于优化搜索方面，其结果表明该行为在优化效果上具有较大潜力。其位置更新公式定义如下：

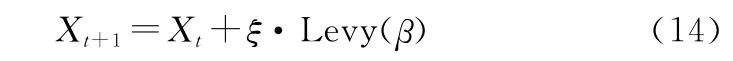
式中：是步长缩放因子；Levy（）表示Lévy随机路径，Levy（）＝，1＜≤3。

另一个是以发现概率P丢弃一部分位置并产生相同数量的新位置代替，位置的更新主要采用随机游动的方式，即利用其他位置的相似性。该更新公式为

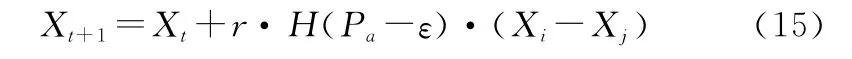
式中：和是服从均匀分布的随机数；（）是单位阶跃函数；X 和X 是其他任意两个位置。

通过这两种位置更新方法可以提高CS算法搜索效率，在较短的时间内收敛到全局最优值。CS算法伪代码如算法2所示。

将CS算法与LS算法结合能够在设定迭代次数内搜索最优解和最优值，有效降低了LS算法的计算复杂度，在网络规模较大时也能快速搜索到较优解。本文将优化后的控制域划分方法称为LS-CS算法。

通过理论分析可知，与k-means算法与谱聚类算法相比较，LS-CS算法能够充分考虑到节点自身的自身特征与节点间的相关性，并且无需预设控制器数量，根据网络结构自适应对网络进行划分，从而得到更好的网络划分结果。因此，本文通过LS-CS算法将网络划分为多个控制域后，在每个控制域中选定节点部署控制器，即完成整个控制器部署的过程。

2.2 PSO-IIW的控制器部署方法

本节基于均衡控制器性能的思想，主要考虑网络时延和控制器负载，具体指标为控制器平均时延、控制域平均时延波动和控制器负载差异度，以优化这3个指标为目标，搜索最佳控制器部署方案。

2.2.1 相关指标定义

控制器平均时延：根据Open Flow协议机制可知，在网络工作时，传输节点与控制器之间以及传输节点之间会进行频繁通信，因此网络模型中的时延包括控制时延和传输时延。控制时延是指控制器与传输节点之间的时延，传输时延是指传输节点之间互相发通信的时延。由于传输时延在划分控制域时已作为参考指标之一，因此网络时延性能只考虑控制器平均时延，其计算公式如下：

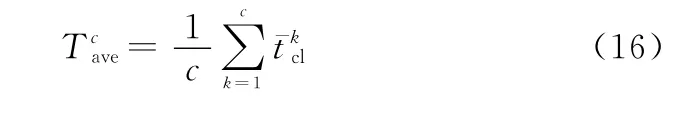
控制域平均时延波动：SD-FANET工作时需要保证通信畅通，因此对时延要求较为敏感，主控制器会根据任务性质和时延要求将其分配给不同的子域，当网络中各子域平均时延相差较大时，平均时延较小的子域会被频繁分配任务，而平均时延较大的子域活跃程度相对较低，这会使得整个网络负载不均衡，网络效率较低。因此，在保证全局平均时延符合要求时，还要确保各控制域时延差异在一定范围内，因此定义控制域平均时延波动指标，其计算公式为

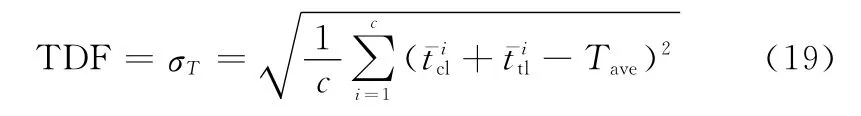
控制器负载差异度：当前文献定义控制器负载差异度时仅考虑控制器域内的传输节点数量，当各域内的传输节点数量相同，但流量请求差异较大时，当前概念认为控制器负载差异度为0，这显然是不够完善的。因此，本文将控制器负载差异度定义为各控制器域内的节点平均请求量与全局平均请求量的标准差，其计算公式为

在选择控制器部署方案时，期望存在一个最佳方案能够使得以上3个指标均达到最优，但这往往是难以实现的。因此，本文对各个目标函数进行线性加权，将该问题转化为单目标优化问题，即

式中：f （＝1，2，3）分别表示制器平均时延、控制域平均时延波动和控制器负载差异度；λ为目标函数f 的权重系数，其值由熵值法确定。求解λ的步骤如下。

归一化处理将指标同质化：

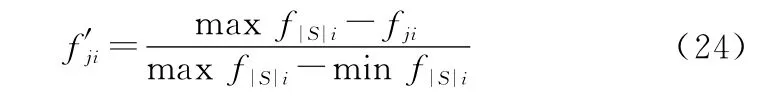
计算每个指标的熵值：

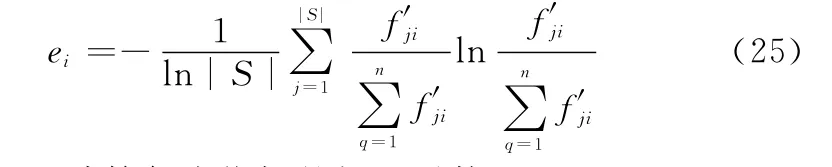
计算每个指标的权重系数：

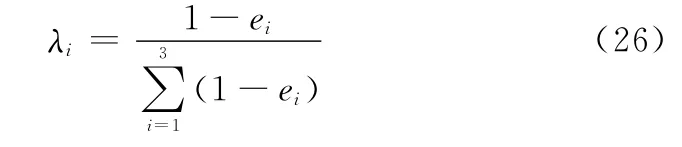
将权重系数代入即可得到目标函数解析式。

由于控制器部署问题比网络划分问题的复杂度更低，可以采用简单且能快速收敛的PSO-IIW对目标函数进行求解。

2.2.2 PSO-IIW算法

传统粒子群算法的收敛能力取决于惯性权重系数，当较大时，全局收敛能力强而局部收敛能力弱；当较小时，全局收敛能力弱而局部收敛能力强。为了避免算法陷入局部最优，期望算法运行前期粒子运动速度较快，同时为了防止偏离全局最优，期望算法运行后期粒子运动较慢。因此对惯性权重系数进行改进，令改进后的惯性权重系数为

式中：为最大惯性权重系数；为当前迭代次数；为最大迭代次数。PSO-IIW算法伪代码如算法3所示。

在输出最优部署方案后，将该方案下的相应节点设为控制器部署位置，其负载请求归零。在此基础上，根据节点时延、控制器负载等相关指标，根据计算结果评估输出方案的可靠性。

3 仿真实验

3.1 仿真参数设置

本文采用Matlab作为仿真平台，由于整个部署过程分为两个阶段，因此仿真实验也分为控制域划分和控制器部署两个阶段以此进行。控制域划分阶段的仿真参数如表1所示。

表1 仿真参数设置-1Table 1 Simulation parameter setting-1

在控制器部署阶段，设置控制器容量＝8，采用该条件下的划分结果作为输入，其他仿真参数如表2所示。

表2 仿真参数设置-2Table 2 Simulation parameter setting-2

通过计算，得到在＝8时，3个指标的权重系数如表3所示（保留3位有效数字）。

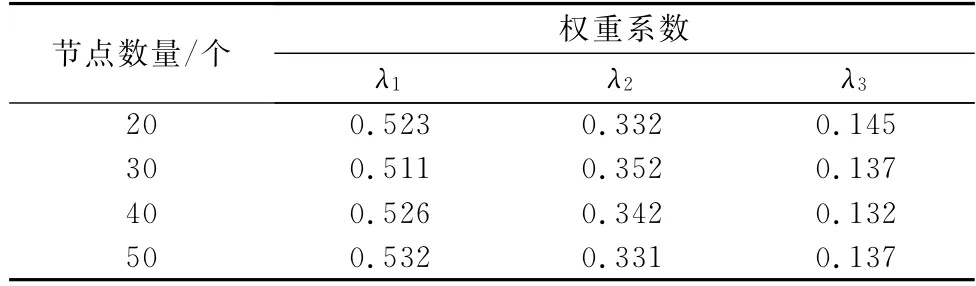
表3 权重系数Table 3 Weight coef ficient

3.2 仿真分析

在控制域划分时，期望以最少的控制器达到控制整个网络的目的，这既可以使得网络的可靠性得到保证，也能够降低部署成本。本文将LS-CS算法与谱聚类算法和k-means算法进行比较，在不同约束条件下得到的结果如图2和图3所示。

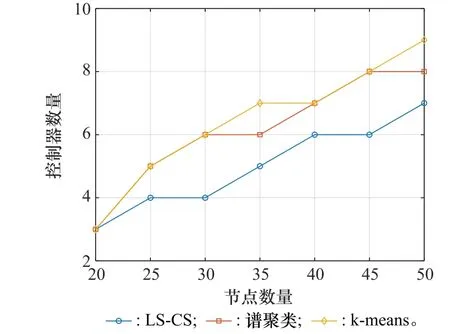
图2 控制器数量与节点数量的关系Fig.2 Relationship between the number of controllers and nodes

图3 控制器数量与控制器容量的关系Fig.3 Relationship between the number of controllers and the capacity of controllers

图2为在给定控制器容量＝8时，控制器数量随网络规模的变化。由图2可知，在控制器容量确定时，同等网络规模下，与k-means算法和谱聚类算法相比，LS-CS算法所需的控制器数量最更少，根据式（1）可知，本文算法所需的部署成本更低。

图3为在给定网络规模＝50时，控制器数量与控制器容量的关系。由图3可知，在网络规模一定时，3种算法计算得到的控制器数量均随着控制器容量的增大而减少，而LS-CS算法与k-means算法和谱聚类算法相比，在控制器容量相同时的控制器数量也是更少的。这是因为无论是k-means算法还是谱聚类算法，其聚类目标都是最小化时延，而LS-CS算法在其基础上，考虑了节点的关联特征，即网络连通性，综合考虑时延因素和网络拓扑结构，因此能够在相同约束条件下得到更好的结果。综合图2和图3可知，在网络规模和控制器容量都确定的情况下，LS-CS算法性能更加优异。在完成控制器划分之后，本文根据相应指标需求选择PSO-IIW算法搜索最佳控制器部署方法，并与depoly-cd算法、k-center策略和survivor策略进 行比较。

图4表示在不同部署方案下，平均控制时延随网络规模的变化关系。相较于其他3种策略，PSO-IIW 算法对于平均控制时延有一定的优化效果。这是由于在对网络进行划分的阶段，自身特征是在最大时延的基础上定义的，而划分时要求惩罚函数最小，即要求最大时延最低，因此与其他算法相比，平均控制时延得到了一定的优化。由于仿真中设置的指标如通信范围，系统信噪比等相较于实际应用有一定的简化和降低，因此在实际应用中，优化效果将会更明显。随着节点数量的增加，平均控制时延会逐渐降低，这是由于在节点数量增加的过程中，仿真区域是固定不变的，从而导致节点密度增大，节点间的时延也就随之降低了。

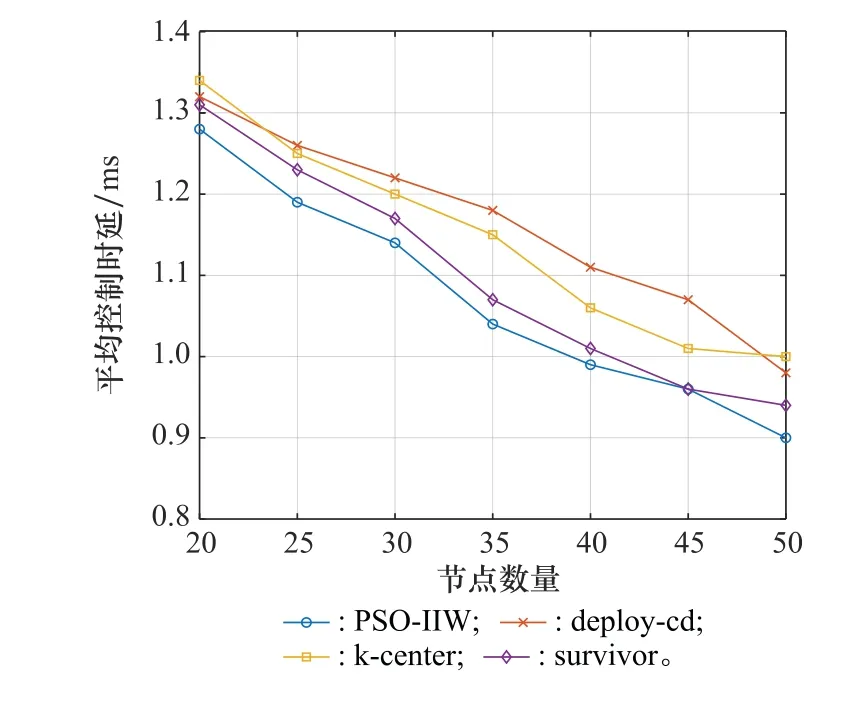
图4 平均控制时延Fig.4 Average control latency

图5表示在不同部署方案下，控制域平均时延波动随网络规模的变化关系。由图5可知，4种方法下的时延波动均随着网络规模的扩大而降低。与其他3种策略相比，PSO-IIW算法的效果更佳。其原因是在网络划分阶段，增加了对节点关联特征的考虑，而关联特征的定义也与时延有关，即在网络划分时，除了确保各个控制域的最大控制时延最低，还保证了各个控制域的平均控制时延相近，从而达到惩罚函数最小的目的，因此本文算法的平均时延波动更稳定。与平均控制时延相似，随着节点数量的增加，网络中的节点密度会增大，从而导致时延降低，且节点更加密集会导致节点间时延趋于相近，因此时延波动也会更加平稳。

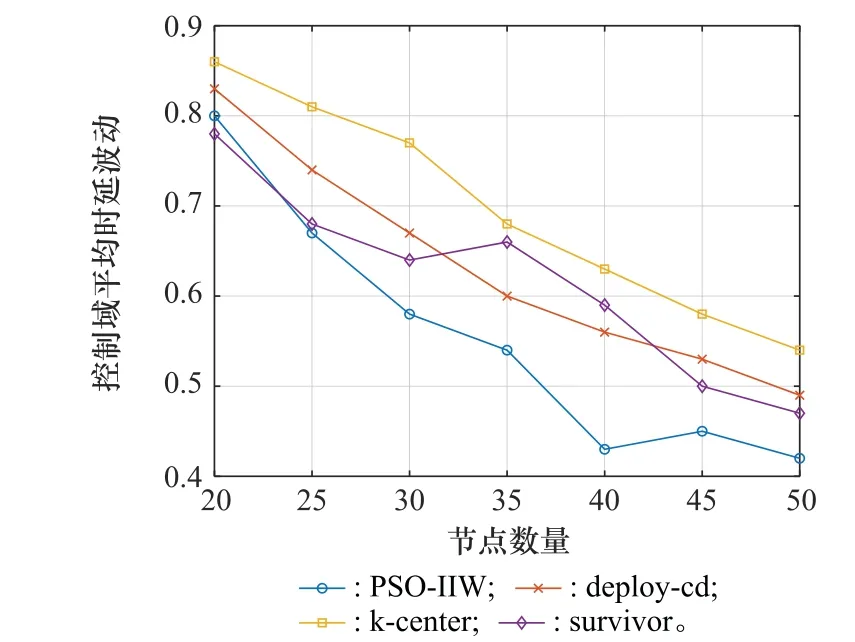
图5 控制域平均时延波动Fig.5 Fluctuation of average latency in control domain

图6为不同部署策略下控制器负载差异度随网络规模的变化情况。由图6可知，随着网络规模的扩大，k-center策略和survivor策略下的控制器负载差异度呈现下降的趋势，控制器负载逐渐趋于均衡。而deploy-cd算法和PSOIIW算法下的控制器负载差异度始终保持平稳的趋势且相比于其他两种策略表现更加优异，其中在PSO-IIW 算法下，该指标始终处于最低的位置，说明PSO-IIW 算法对于部署控制器而言能够体现出更优异的性能。这是因为本文提出了新的负载差异度的概念，在对比算法仅考虑传输节点数量的基础上增加了对节点流量请求的考虑，在此概念下，对比算法的负载差异度增大，对比之下即可说明本文算法能够更好地实现控制器的负载均衡。

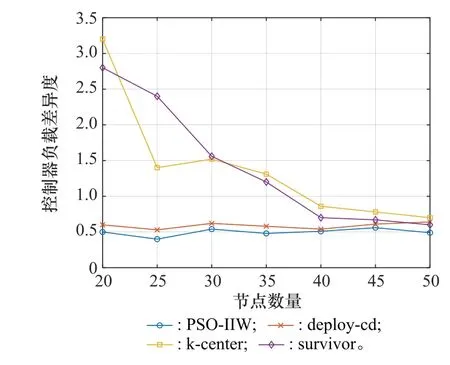
图6 控制器负载差异度Fig.6 Controller load difference

本文提出的LS-CS算法在对网络进行划分时，综合考虑网络节点特征和网络拓扑结构特征，在约束条件下对网络进行划分。通过仿真结果及相应分析能够证明，LS-CS算法能够有效降低网络平均控制时延，稳定控制域平均时延波动并且能够均衡控制器负载。在此基础上采用PSOIIW算法，其目的是能够更加快速地在给定的范围内搜寻到最佳控制器部署位置，从而提高控制器部署效率。

4 结 论

本文将多控制器的部署问题分解成两个子问题解决，首先使用LS-CS算法的控制域划分方法将整个网络划分为满足约束条件的多个控制域，在此基础上采用PSO-IIW 算法在各个域内部署控制器从而完成多控制器部署的整个过程。通过与其他策略的比较，表明LS-CS算法能在保证网络可靠性的情况下降低部署成本，提高划分效率，而PSOIIW算法能够得到更低的时延，同时该算法下的控制器负载更佳均衡，为控制器的高效工作提供了可靠的保障。