多频带互相干处理中多目标相位补偿方法

王 宁，吕晓德，李苗苗，3，刘忠胜

（1.中国科学院空天信息创新研究院，北京 100094；2.微波成像技术国家级重点实验室，北京 100190；3.中国科学院大学电子电气与通信工程学院，北京 100049）

0 引 言

根据傅里叶分析的理论，一个域的更高分辨率需要其变换域具有更宽的支撑区间。因此，为了提高距离分辨率需要加宽发射信号的带宽，例如使用线性调频（linear frequency modulation，LFM）信号。但由于频谱资源以及硬件的限制，无法任意增大单一辐射源的带宽，此时就可以考虑对多频带信号进行相参处理，即将不同子带的信号通过插值和外推的手段进行拼接，从而获得大带宽的信号。

早期多带相参处理的想法由林肯实验室Cuomo等提出，通过使两部雷达发射不同频段的信号，并同时接收这两个频段的回波信号，运用基于拟合模型的插值方法补全处于不同频带信号之间空缺的数据，由此形成宽带信号，提高成像分辨率；近两年，多带相参处理在光子雷达测距和逆合成孔径雷达（inverse synthetic aperture radar，ISAR）领域有所应用。多带相参处理的一个关键技术是对不同频带信号进行互相干处理，使插值后的频带数据在拼接点处具有相位连续性，从而满足相参处理的条件。回波匹配滤波后的频谱体现为全极点模型，Cuomo等认为不同频带信号的频谱会差一个固定相位和线性相位，需要通过非线性优化来实现互相干处理，但没有详细论述所差相位的来源，也没有考虑目标运动带来的影响。多带之间的相位差异一方面来源于观测条件的不同，例如初始相位的不同、回波路径的不同等，另一方面来源于目标运动；一般默认由于观测条件不同导致的相位差异对不同的目标是一样的，而由于目标运动导致的多普勒相位差异是依赖于目标运动速度大小的，且目标速度通常是未知的。文献［8］考虑了在多频带多雷达融合成像中，由于多部雷达观测条件不一致所造成的幅相差异，建立了相关的误差模型，但没有考虑由于目标运动带来的多普勒相位差异。文献［9-14］使用了不同的方法来处理不同频带信号的相位差异，但没有详细考虑目标运动带来的多普勒相位差异。文献［15-17］考虑了存在动目标时的互相干处理，但在做速度补偿时需要估计目标速度，而且没有考虑存在速度不同的多目标时，需要补偿不同的相位，也没有考虑子带之间脉冲重复时间（pulse repetition interval，PRI）不同带来的影响。文献［18-19］考虑了载频不同导致不同频段数据的多普勒维尺度不同，利用Keystone变换使其尺度统一；但未考虑PRI不同对多普勒维尺度的影响，而原始的Keystone变换是无法处理该影响的。

综上，虽然以往也有文献考虑到目标运动会带来子带之间的相位差异，但还尚未有文献考虑到当多带信号的载频、PRI都不同，并且回波中存在不同速度目标时，每个目标的多普勒相位在不同频带上是不同的，这导致不能通过乘以一个统一的修正相位来补偿不同频带上的多普勒相位信息。本文针对这一问题，在已有工作的基础上，提出一种基于Keystone变换的多普勒相位补偿方法，在速度未知的情况下，可以在补偿距离徙动的同时补偿不同频带信号上的多普勒相位，在此基础上通过插值的方法对不同频带进行相参处理拼接成大带宽信号，从而提高距离分辨率。通过理论分析和仿真验证说明该方法的可行性，该方法可以在多目标场景下补偿多普勒相位。

本文后续结构如下：第1节建立了多频带相参处理模型，详细分析了多带信号之间相位差异的形式；第2节简洁介绍了Keystone变换；第3节给出了基于Keystone变换的多普勒相位补偿方法的理论分析；第4节介绍了信号处理流程；第5节给出在单目标及多目标场景下的仿真结果，并利用已有的单频带实测数据进行了半实测半仿真试验，验证方法的可行性；第6节对本文内容进行了总结，并说明了应用价值。

1 多频带相位差异模型

假设有两部脉冲体制的雷达在相近的时间内发射信号，所用的两部雷达的脉冲信号应保证在一个相干处理间隔（coherent processing interval，CPI）之内，但所发信号的载频、PRI、时宽、带宽均可不同，并且两部雷达之间的距离远小于目标的距离，这样可以保证目标响应在两部雷达之间的观测相关性，条件约束与常规脉冲雷达类似。假设脉冲多普勒雷达每个CPI中接收个脉冲回波，则回波模型可以表示为

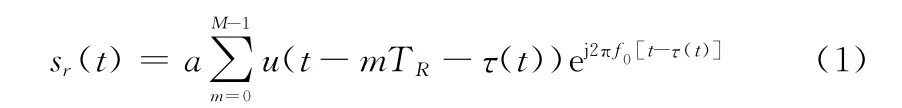
式中：是一个常数，表示回波大小；（）是所发射带宽为的信号；T 是PRI；是载频；（）是回波时延。假设目标在雷达视线方向上匀速运动，则有（）＝-2／c，＝2／c，其中，是动目标的初始距离。假设动目标在一个脉冲发射到接收的过程中距离是不变的，则经过下变频后可以表示为

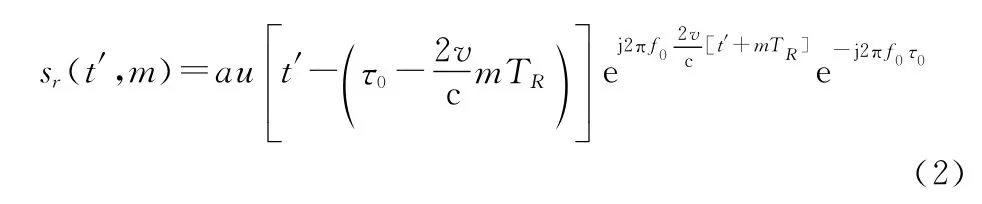
式中：＝-m T ，表示快时间，表示慢时间。s（，）做完匹配滤波后，假设频谱幅度近似为常数，则在快频率-慢时间域有如下形式：

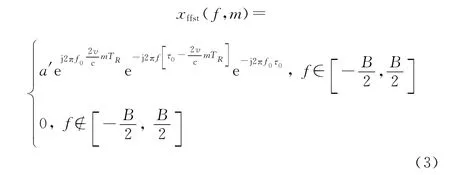
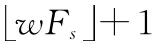
式中：f 为目标的多普勒；f 为目标的快频率；是系数；是频域采样点数。表达式分别为

可以看出，匹配滤波后的信号在快频率 慢时间域呈现一个二维复正弦的形式。两部雷达信号的回波可以表示为

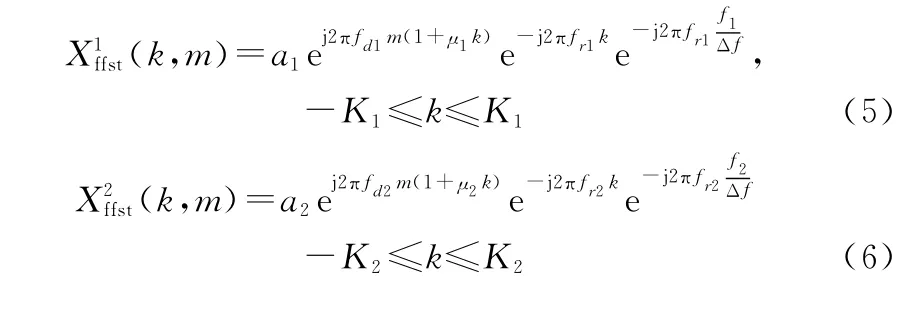
式中：f 、f 分别表示目标在两部雷达回波中的多普勒；f 、f 分别表示目标在两部雷达回波中的快频率；两部雷达信号回波中的取值边界分别用和表示，计算方式与相同。

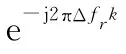
当以式（5）为准，调整式（6）的线性相位、固定相位和幅度后，可将式（5）和式（6）重写为

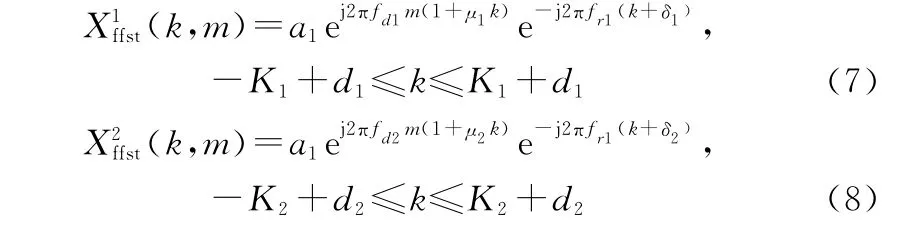
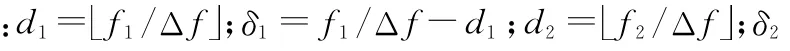
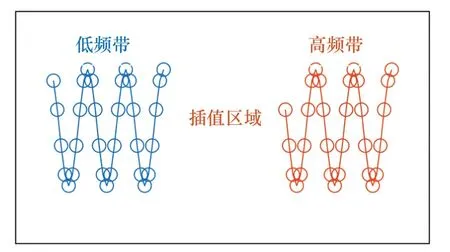
图1 带宽插值Fig.1 Bandwidth interpolation

以往文献只考虑了上述的固定相位，线性相位以及幅度的差异，并将对其补偿的过程称为互相干处理，但是很少有考虑第一个复指数项的差异，即动目标多普勒相位的差异，该差异具有速度依赖性，多目标场景下不能通过乘以统一的相位来补偿；而且速度通常是未知的，需要在速度未知的情况下去补偿。

2 Keystone变换

由于观测目标与雷达之间存在相对运动，时延在每一个脉冲回波中都不一样，当相对运动速度太大时，这些时延的差异不可忽略，会对之后的相参积累造成影响，即距离徙动。Keystone变换是常用的矫正线性距离徙动的方法，最早在合成孔径雷达（synthetic aperture radar，SAR）领域被使用，后来也被用于脉冲多普勒体制雷达。距离徙动的因素正体现在式（4）中的“1＋”，这一项使得快频率维“”和慢时间维“”存在一定的耦合，不能通过简单的二维快速傅里叶变换（fast Fourier transform，FFT）实现相参处理。为了处理掉这一项，引入了坐标变换式，即Keystone变换：

但Keystone变换并不适合于速度出现模糊的情况。当速度出现模糊时，f （1＋）＞1，令f 为模糊后的多普勒频率，则

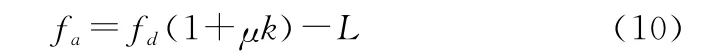
式中：f ∈［-0.5，0.5］；为正数，表示模糊程度。如果只进行Keystone变换的话，则

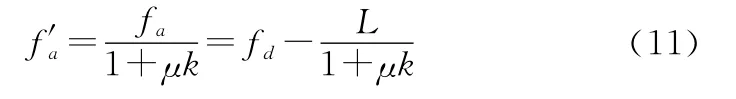
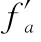
3 基于Keystone变换的多普勒相位补偿

假设两部雷达发射信号的载频、PRI分别为和，和，并且其f 都相同，则在快频率-慢时间域可以表示为

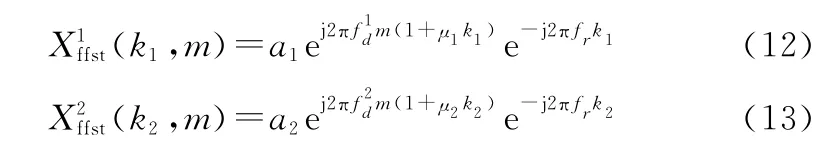
以往文献为了将两段频谱互相干，往往只是乘以一个e ，e 是为了补偿f ，e是为了补偿其余的相位因素，其中，通常被称为固定相位。此处已经假设了f 相同，所以可以暂时不考虑。用Δ来表示目标在两部雷达回波中的多普勒相位差异，则Δ可具体表示如下：

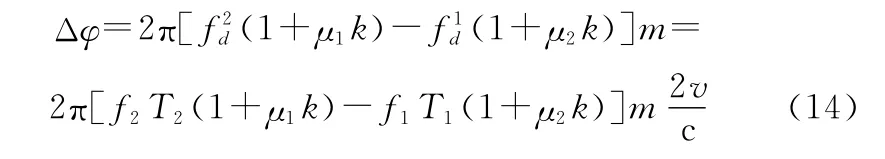
对于不同的，Δ往往是不同的，即使忽略距离徙动因素1＋，有

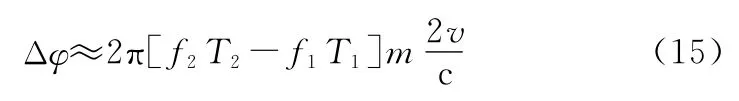
也可以看出对于不同速度的目标，由于信号载频和PRI的不同，导致需要补偿的相位是不同的，不能一概而论。为了可以对不同速度目标的多普勒相位统一补偿，在无速度模糊的情况下可以对式（12）使用式（9）的坐标变换，而对（13）使用坐标变换。

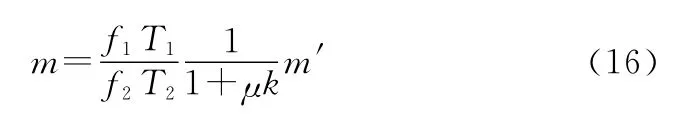
这样就可以以信号1为基准将不同速度目标的多普勒相位统一补偿；要注意，应以无模糊间隔大的信号为基准进行补偿。与原始的Keystone变换不同，新引入的变换式（16）考虑了脉冲的PRI，也正是因为加入了PRI才能使得两部雷达回波信号中的多普勒相位补偿一致。文献［15-17］为了补偿两部雷达回波中与速度有关的相位差异，都是先对速度进行估计再进行补偿，这个思路对多目标不合适。而本文将与速度有关的相位差异归结为多普勒相位差异，新的变换可以在速度未知的情况下对多目标的多普勒相位进行补偿。

当存在速度模糊时，在Keystone变换和多普勒相位补偿后，两个信号的多普勒如下所示：

为了对应实际的模糊后的多普勒，需要分别予以／（1＋）和［／（1＋）］·［／］的补偿；这里区分和是因为同一目标在两部雷达信号回波中的模糊程度不同。

4 处理流程

图2是两部雷达信号多频带相参处理的流程，IFFT表示逆FFT（inverse FFT）。该处理流程可以很容易拓展到多部雷达信号的情况，下面对关键步骤作简要说明。

图2 信号处理流程Fig.2 Signal processing flow

4.1 数据接收

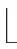
4.2 匹配滤波

在频域进行匹配滤波后，由于信号本身的谱往往是有起伏的，体现在

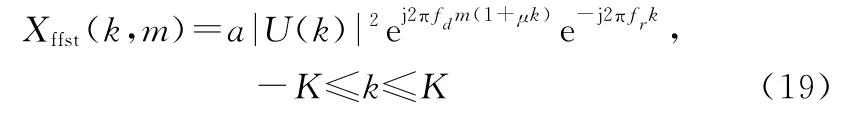
有时为了消除这种起伏带来的影响，可以除以｜（）｜最终得到式（4）。对于LFM信号，当时宽带宽积较大时，可以忽略｜（）｜，认为其近似为常数。

又由于采样频率F往往大于信号带宽，频域上有一些点是不在信号带宽范围内的，可以直接不使用，即省去∉［-，］的点。有些信号，例如LFM 信号，在其频谱边缘会出现Gibbs现象，在频域取点时需要省去出现Gibbs现象的点，以免其对插值过程产生影响。例如图3是LFM信号的频谱，取数据时应取红框中的数据，避开出现Gibbs现象的位置。

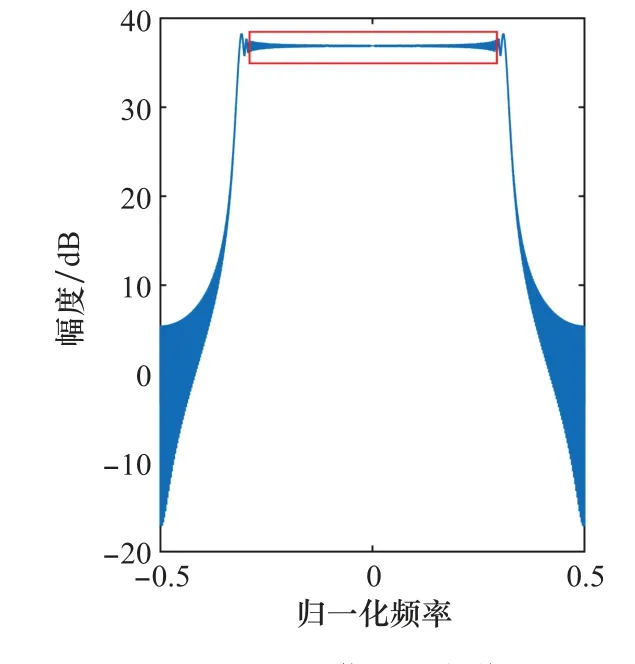
图3 LFM信号幅度谱Fig.3 Amplitude spectrum of LFM

4.3 互相干处理

互相干处理在此指的是补偿不同信号之间的线性相位、固定相位以及幅度，关于互相干处理的方法可参考［1，8-13］；因为多普勒相位补偿是单独对信号2在慢时间维进行处理，其他相位和幅度差异的补偿在慢时间维的数据上表现为乘以一个复常数，不影响该处理，所以本文只考虑多普勒相位的差异，仿真时假设不存在线性相位、固定相位以及幅度的差异。

4.4 插值

当两段频谱没有重合部分时，需要对其缺失部分进行插值。首先，插值之所以放在“慢时间FFT”之后，是因为“慢时间域”变换到了“慢频率域”，而“慢频率域”其实是多普勒维，在多普勒维度上可以将低速干扰和高速目标分开，这样在进行频谱外推时可以减少非目标成分的干扰。插值的方法有很多种，例如基于有理谱模型的方法，基于状态空间模型的方法，基于非参数自适应滤波器组的方法，以及基于稀疏重构的方法。本文采用基于自回归模型（autoregressive model，AR）的方法，关于AR模型参数估计的方法有很多，推荐使用Burg算法，Burg算法计算效率高，保证外推系数的稳定性，即没有极点位于单位圆之外，而且对噪声更不敏感；AR模型的阶数一般选择小于／3，但对于低信噪比的信号需要更高的阶数。

5 仿真

5.1 单目标

仿真生成参数不同的LFM信号的回波来模拟不同雷达信号的回波，参数如表1，回波脉冲数为128，信噪比（signal to noise ratio，SNR）为-15 dB，SNR定义为10lg（／），其中，是信号的幅度，是噪声方差。并且以下仿真中在快时间维和慢时间维都没有加窗来降低旁瓣。

表1 单目标参数Table 1 Single target parameters

图4（a）和图4（b）分别是信号1和信号2经过传统相参积累（包括了Keystone变换）的结果，可以看出，由于载频和PRI的不同，两者的峰值不在同一距离多普勒单元，分别处在（83 Hz，150 m）和（666.7 Hz，150 m），因此无法在同一多普勒单元上通过插值来实现相参处理，因为此时同一多普勒单元对应着不同的目标速度。图4（c）是以信号1为基准，对信号2进行多普勒相位补偿之后的距离 多普勒图，可以看出其目标多普勒变为83 Hz，与信号1的距离 多普勒图中的目标多普勒一致，说明多普勒相位已经得到补偿，即同一运动目标在两个距离 多普勒图中处在同一多普勒单元；在此基础上，可进一步进行相参处理。图4（d）是频带相参处理后的结果，可以看出距离分辨率有明显的提升，间接说明了信号2的多普勒相位已经调整的和信号1的一样。

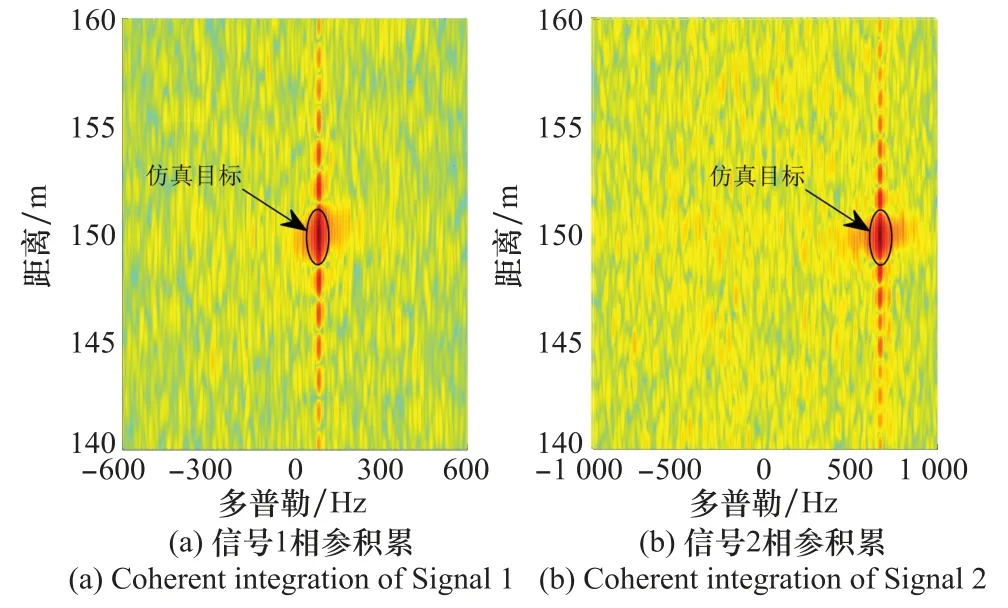
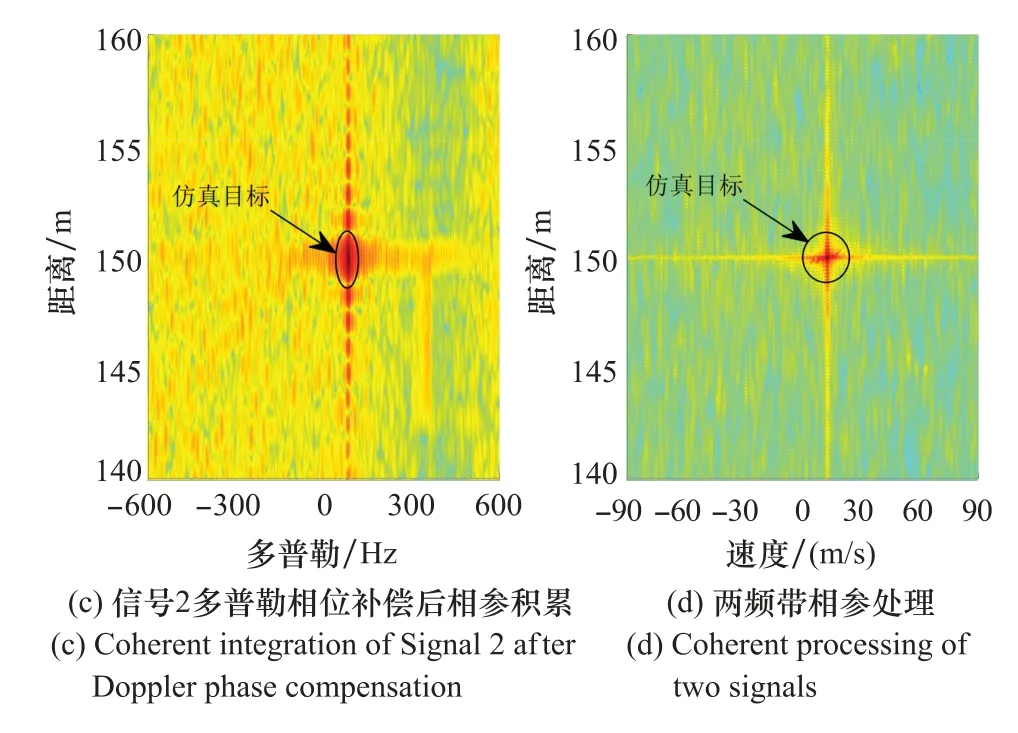
图4 单目标仿真Fig.4 Single target simulation

5.2 多目标

仿真生成参数不同的LFM 信号的回波，参数如表2，回波脉冲数为128，SNR为-15 d B；＝0.8／，这样传统相参积累在距离向是分不开两个相近目标的。

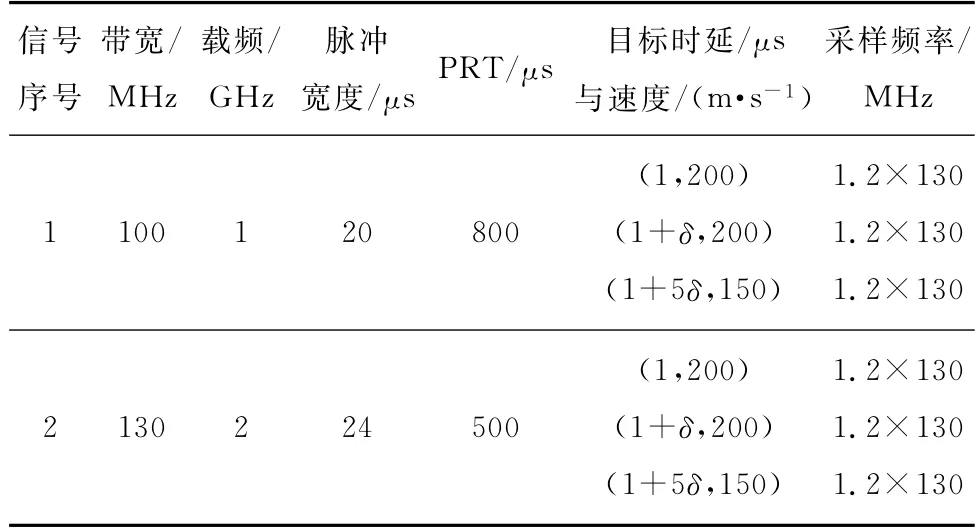
表2 多目标参数Table 2 Multi-target parameters

图5（a）和图5（b）分别是信号1和信号2经过传统相参积累（包括了Keystone变换）的结果，可以看出由于多普勒相位没有补偿，目标处于不同的多普勒单元上，而且不能够将相近的目标区分开，3个目标在信号1和信号2的距离-多普勒图中所处的距离多普勒单元分别为（83 Hz，150 m）和（666.7 Hz，150 m），（83 Hz，150.9 m）和（666.7 Hz，150.9 m），（-250 Hz，154.6 m）和（0 Hz，154.6 m）；图5（c）是以信号1为基准，对信号2进行多普勒相位补偿之后的距离 多普勒图，可以看出3个目标的多普勒与图5（a）信号1中的一致，说明多普勒相位已经得到补偿，在此基础上，可进一步进行相参处理。图5（d）是频带相参处理后的结果，距离相近的两个目标被区分开来，说明频带相参处理提高了分辨率，进而间接说明了信号2的多普勒相位已经调整得和信号1的一样。

图5 多目标仿真Fig.5 Multi-target simulation

5.3 半实测半仿真

经过外场试验测得一组带有动目标的单频带实测数据，所测得的动目标为民用飞机，距离约56 km。利用已有的单频带实测数据，仿真生成与其对应的另一频带模拟回波数据，模拟回波数据中目标的距离与速度从实测数据中估计得到，所添加的高斯白噪声方差也是利用实测数据估计得到的，并进一步调整模拟回波数据中信号回波幅度的大小，使其相参积累后的SNR与实测数据基本一致；其他相关参数如表3所示，由于保密需求，信号的真实参数用符号代替。

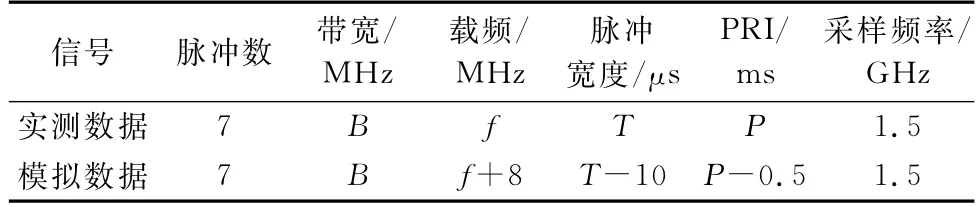
表3 实测数据与模拟数据的参数Table 3 Parameters of measured data and simulated data

对实测数据和模拟数据分别在不使用本文多普勒相位补偿方法和使用本文多普勒相位补偿方法的情况下进行多频带相参处理，结果如图6所示，可以看出，使用本文方法可以在目标所在位置积累出更窄的峰值。图7是目标所在位置的距离维曲线，可以看出，通过利用AR模型对频域数据进行有效外推可以提高距离分辨率，但在进行多频带相参处理时，如果不使用本文多普勒相位补偿方法距离分辨就无法得到有效提高，这说明多普勒相位补偿的必要性以及在该场景下本文所提方法的可行性。

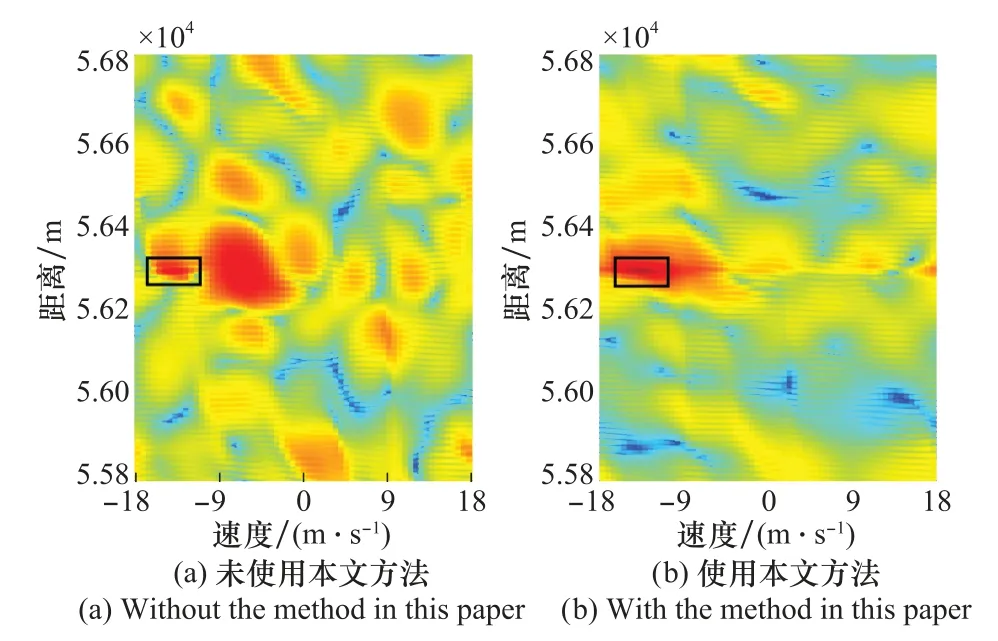
图6 半实测半仿真结果Fig.6 Semi-measured and semi-simulation result

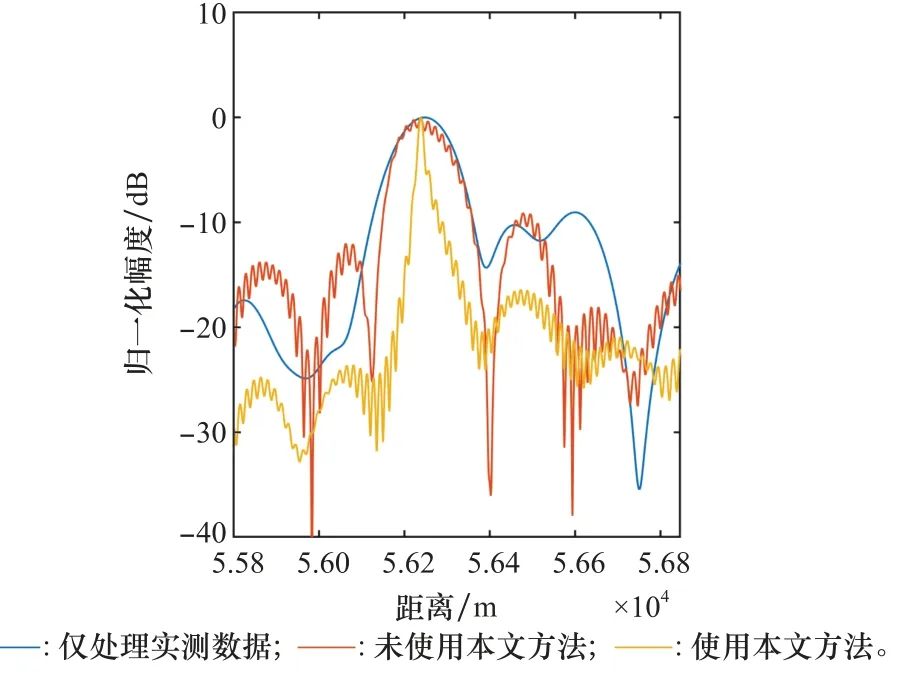
图7 距离维对比Fig.7 Contrast in range dimension

6 结 论

多频带相参处理可以应用于双／多基雷达的目标测距和成像领域，其关键技术是互相干处理，互相干处理是为了补偿子频带之间的相位差异，其中就包括多普勒相位差异。本文在两部脉冲雷达发射信号载频、PRI不同的场景下，针对不同载频、PRI导致同一动目标在两部雷达的回波中的多普勒相位不同，影响多频带数据之间相参处理的问题，提出一种基于Keystone变换的多普勒相位补偿方法，该方法可以在距离徙动校正的同时以及速度未知的情况下完成多目标多普勒相位补偿，为多源多频带场景下的多目标信号互相干处理提供了一种新的途径。通过单目标及多目标场景的仿真以及半实测半仿真实验，验证了该方法可以在速度未知的情况下对多普勒相位进行补偿，补偿后的信号可以进一步相参处理，提高分辨率。