广义二维多项式混沌映射及其在信息传输中的应用

闫文浩，姜子敬，黄欣，朱淑娟，丁群

（1.黑龙江大学电子工程学院，黑龙江 哈尔滨 150080；2.澳大利亚佛林德斯大学科学与工程学院，通斯利 SA 5042）

0 引言

非线性动力系统在许多研究领域都受到越来越多的关注[1-2]。混沌映射是一种典型的非线性映射，其具有初值敏感性、内禀随机性、遍历性、拓扑传递性和正的Lyapunov 指数等优良特性[3-5]。这些特性使混沌映射更适用于密码学、信号处理、神经网络等领域[6-9]。

现有混沌映射在工程应用中存在许多缺点。1)由于经典混沌映射结构比较简单，随着计算机计算能力的提升，混沌映射的控制参数，甚至整个序列都可以被估计出来。2) 这些混沌映射都存在弱混沌现象，即控制参数发生微小的变化，就会造成混沌现象的消失。3) 由于动力学退化的问题，这些混沌映射会产生严重的安全缺陷，从而影响基于混沌的应用[10-11]。

为了改善混沌映射的动力学特性，许多新的混沌映射被提出。新的混沌映射大致分为两类，第一类是基于现有混沌映射提出的改进混沌映射，文献[12]提出了离散忆阻器模型耦合一维混沌映射，得到了新的二维混沌映射，文献[13]提出了将3个不同的一维映射嵌套生成分段函数，文献[14-15]将2 个一维混沌耦合生成二维混沌映射；第二类是基于线性函数或非线性函数构建新的混沌映射，文献[16]基于“周期三蕴含混沌”提出了新的二维混沌映射并研究了该映射的动力学特性，文献[17]提出了三维超混沌映射并基于该混沌映射提出了一个混沌传输方案，文献[18]基于三维分段映射提出了一个图像加密方案。上述研究都比较特殊，没有一种广义的表达式，不具有一般性。文献[19]根据相似矩阵的观点，提出了一个高维离散混沌映射，但该映射只针对高维混沌映射，不适用于二维混沌映射。文献[20]根据Lyapunov 指数的定义反向构造了一个二维多项式混沌映射，基于这种构造方法，映射中的一个方程必为线性映射。如果初始值和控制参数选取特殊值，那么映射的维数就会降低，映射所产生序列的复杂度不能满足要求。为此，本文提出一种二维多项式混沌映射，其可以产生具有稳健性和既定复杂行为的二维混沌映射。理论仿真和实验结果表明了该映射的优越性。本文的主要工作总结如下。

1) 本文提出了一个广义二维多项式混沌映射，通过一个命题给出不同控制参数和多项式最高次数，得到一系列具体的二维混沌映射。

2) 理论分析结果表明，二维多项式混沌映射可以产生稳健混沌和期望的Lyapunov 指数。

3) 为了阐述该映射的有效性，本文给出了一个具体的数值实例，特性分析表明，本文提出的混沌映射比Hénon 映射、2D-SLM 和 2D-LSMCM 动力学特性更为复杂。

4) 本文将不同混沌映射应用于RM-DCSK 通信方案，实验结果表明，本文映射更适合于信息传输。

1 二维混沌映射

本节介绍3 种典型的二维混沌映射，并通过分岔图和相空间运动轨迹分析其动力学特性。由于现有映射只在一定的参数范围内存在混沌行为，且混沌序列的输出不均匀，本文提出了一个二维多项式混沌映射。首先，通过设计一个命题，从理论上给出了系统存在混沌行为的参数取值。然后，选择不同控制参数和多项式最高次数，得到许多具有稳健混沌和既定复杂行为的二维混沌映射。最后，通过平衡点分析研究了该映射的稳定性。

1.1 现有二维混沌映射

Hénon 映射作为经典的二维离散混沌映射，其数学表达式为

其中，xn和yn为映射的状态变量，a和b为映射的控制参数。当参数时，映射为混沌状态。近年来，许多学者也提出了改进的二维混沌映射，文献[14]以一维Logistic 映射和Sine 映射为基础，提出了一种新的二维混沌映射（2D-SLM,two dimensional sine-logistic map），其数学表达式为

其中，xn和yn为映射的状态变量，a和b为映射的控制参数。当参数时，映射为混沌状态。文献[15]同样以一维Logistic 映射和Sine 映射为基础，提出了另一种新的二维混沌映射（2D-LSMCM,two dimensional logistic-sine-modulated-coupling map），其数学表达式为

其中，xn和yn为映射的状态变量，a和b为映射的控制参数。当参数时，映射为混沌状态。对于一个混沌映射，其分岔图刻画了不同参数情况下的运动轨迹。通过分岔图可以直观地衡量混沌映射在不同控制参数下的遍历性和非周期性。图1的前两列展示了3 个混沌映射的2 个状态变量xn和随控制参数b变化的分岔图（控制参数a固定），可以看出3 个映射的分岔图只有在很小的区域内才表现出混沌状态，并且出现了周期窗。若控制参数发生偏差，映射就有可能从混沌态退化为周期运动。图1 的最后一列描绘了3 个映射在固定参数下的相空间运动轨迹，可以看出Hénon 映射的输出序列只分布在二维平面的一小块区域，而其他映射的输出序列也分布在特定区域。这说明3 个映射的输出序列分布不具有均匀性，会使混沌映射在图像加密、信息传输、信息安全领域受到影响。

图1 二维混沌映射的分岔图和运动轨迹

1.2 广义二维多项式混沌映射

为了增强混沌映射的动力学特性，本文提出了一种二维多项式混沌映射。其数学表达式为

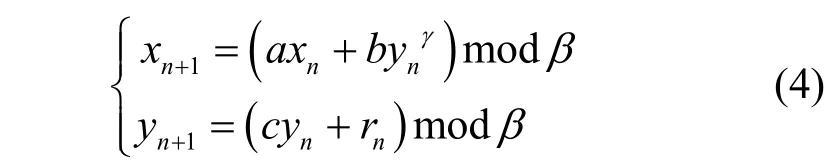
其中，xn和yn是映射的状态变量，a,b,c,r是映射的控制参数，γ是多项式最高次数，β是取模系数。为防止状态变量yn塌陷为一个固定值，本文将rn取为随机扰动量。下面，通过一个命题来讨论该映射何时处于混沌状态。

1.3 混沌行为证明

Lyapunov 指数是用来证明一个映射是否为混沌最有效的手段。本文采用Lyapunov 指数来判别所构造的映射。

定义1[21]若一个二维映射是全局有界的，且至少有一个正的Lyapunov 指数，则该映射处于混沌状态；若具有2 个正的Lyapunov 指数，则处于超混沌状态。

一个二维离散动力学映射的2 个Lyapunov 指数计算表达式为

其中，J(·) 是系统第i次迭代时的Jacobian 矩阵。

命题1若式(4)的控制参数则该映射是混沌的。若则该映射是超混沌的。

证明式(4)第i次迭代的Jacobian 矩阵为

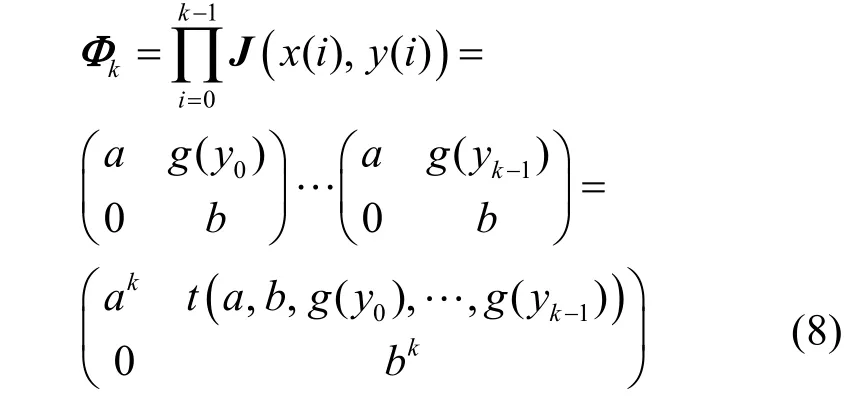
那么该映射的2 个Lyapunov 指数的推导过程为

同理，LE2=lnb。由于式(4)加入了取模运算，因此映射的输出必定是全局有界的。若控制参数，则必有一个正的Lyapunov 指数，则该映射处于混沌状态。若控制参数且则2 个Lyapunov 指数都是正的，则该映射处于超混沌状态。证毕。

1.4 平衡点及稳定性

平衡点是指动力学系统下一时刻的运动状态与当前时刻的状态一致，其数学表达式为二维混沌映射所有的平衡点都是方程式(11)的解。

通过对式(11)进行求解，可以得到许多不同的平衡点。显然，(0，0) 是上述方程的一个解，因为不同的参数设置，上述方程会出现很多非零平衡点。不妨设系统的非零平衡点为，混沌映射的Jacobian矩阵为式(7)。从式(7)可以看出，Jacobian 矩阵的2个特征值为λ=a，λ=b，即特征值只取决于控制参数，而与状态变量无关。当参数a＞1 且b＞1 时，Jacobian 矩阵的2 个特征值始终为那么二维混沌映射模型所有非零平衡点都是不稳定的，从而系统可以表现出混沌状态甚至超混沌状态。

2 数值实验

本节按照命题1 给出的结论，构造了一个具体的二维多项式混沌映射。目前，判断混沌特性的主要方法主要有相轨迹（相图）分析法、分岔图、Lyapunov 特征指数法、分数维分析法、复杂度测度法、自功率谱谱分析法等[22]。本文通过相图、分岔图、Lyapunov 指数、样本熵（SE,sample entropy）、关联维数（CD,correlation dimension）分析其动力学行为，并通过与现有二维混沌映射进行对比，以阐述该映射的优良特性。

2.1 数值实例

为了方便计算，本文取γ=2，该二维多项式混沌映射的数学表达式为

由命题1 可知，若要使式(12)处于混沌状态，则令a=2，b=3，c=1.7，β=1，rn是(0,1)范围的一个随机数。为了方便讨论，本文将控制参数的范围取为a,b,c∈(1,5)。

2.2 分岔图与运动轨迹

对于一个混沌映射，其分岔图刻画了不同参数情况下的运动轨迹。通过分岔图，可以直观地衡量混沌映射在不同控制参数下的遍历性和非周期性。动力学系统的分岔图显示了在不同参数下系统在相空间中所经过的点，为研究混沌的性质提供了一种直观的方法。图2 以三维视角展示了该映射随2 个参数变化的分岔图。从图2 中可以看出，状态变量xn在不同的控制参数下都均匀地分布在整个空间。图3 展示了映射在固定参数下的运动轨迹，随着迭代次数的增加，系统的输出范围为[0,1) 。

图2 映射随2 个参数变化的分岔图

图3 映射在固定参数下的运动轨迹

2.3 Lyapunov 指数

在非线性动力学理论中，Lyapunov 指数可有效地描述映射随时间演化时映射对初值的敏感性。对初始条件的敏感性是混沌的一个重要特征，即相空间中的2 个轨道彼此接近，随着时间的推移，它们会以指数形式分离。若Lyapunov指数为负，表明系统的相体积在运动方向上是收缩的，即该方向的运动是稳定的；若Lyapunov指数为正，表明系统的相体积在某个方向上是不断膨胀和折叠的，导致吸引子中本来邻近的轨迹变得越来越不相关，从而使初始状态不确定的映射随时间演化时，其行为变得不可预测，即初值敏感性。此时，映射的运动状态是混沌的。Lyapunov 指数的计算在前文已做过叙述，本节不做赘述。该映射随控制参数变化的Lyapunov指数谱如图4 所示。从图4(a)和图4(b)可以看出，Hénon 映射和2D-SLM 只有在极小参数范围内有正的Lyapunov 指数；从图4(c)可以看出，系统在(1,5]参数范围内都有正的Lyapunov 指数，与前面给出的理论分析一致。如果映射的控制参数发生微小变化，前2 个映射会出现弱混沌，甚至退化为周期行为，而本文映射仍然保持混沌状态。其次，映射在(]1,5 参数范围内具有2 个正的Lyapunov 指数，因此映射在(]1,5 范围内处于超混沌状态，相较于前2 个映射，本文映射展示了稳健超混沌行为和更复杂的动力学特性。

图4 映射随2 个参数变化的Lyapunov 指数谱

2.4 样本熵

样本熵是基于近似熵提出的一种新的生物时间序列复杂度的分析算法[23-24]。该算法取消了近似熵中的自匹配，使其计算更为简单，计算时间大大缩短，计算的条件概率也更加精确。该算法在计算上采用去除与自身模板比较的方式，扩大了与阈值相比较的偏差值，可以更加准确地估计新数据出现的概率，降低了近似熵的误差，是时间序列复杂度量化更加精确的一种算法。近似熵值越接近0，时间序列的自相似性越强，产生新数据的概率越小，复杂度越低；近似熵值越大，映射的复杂度越高。图5 展示了不同映射随参数变化的近似熵值。从图5(a)和图5(b)可以看出，2 个映射在特定范围内可以取得正的近似熵值，且近似熵值都介于(0 1)，；从图5(c)可以看出，二维多项式映射的近似熵值在整个区间都是正的，且近似熵值也大于前2 个映射。这说明了该映射产生的混沌序列具有很高的复杂度，可应用于图像加密、信息处理和信息传输等领域。

图5 映射随2 个参数变化的近似熵值

2.5 关联维数

作为分形维数的一种，关联维数研究的是时间序列所占据空间维数[25]。时间序列的关联维数的表达式为

其中，m表示序列的嵌入维数，r表示嵌入空间球的半径，表示关联函数，其表达式为

其中，θ(x) 表示阶跃函数表示欧氏空间中Xi与之间的距离，N表示相空间中点的个数。如果一个非线性映射其输出序列的关联维数大于0，则表明该非线性映射具有混沌行为。数值越接近映射的维数，映射的混沌行为越复杂。表1 展示了4 个混沌映射在给定参数下的关联维数。相较于其他映射，二维多项式混沌映射的关联维数大于其他3 个系统，表明二维多项式混沌映射产生的时间序列具有更高空间维数。

表1 4 个混沌映射在给定参数的下的关联维数

2.6 随机性测试

为了证明混沌输出序列的伪随机性，本文通过NIST SP 800-22 进行测试。对于NIST 套件中的15项测试，其显著性水平设置为1%。当P〉0.01 时，该二进制序列就被认为是随机的，且其置信度为99%，否则被认为是非随机的。在本文测试中，给定初始值和控制参数，由于混沌序列的输出都介于本文采用等式，将十值序列转化为二值序列。其中是向下取整函数，di是混沌输出序列，α是一个很大的数来影响序列的数值，β是一个整数。设，可以得到8 bit 的二进制序列。然后对2 个混沌序列进行NIST 测试，测试结果如表2 所示。在表2 中，所有测试均测试成功，表明所提映射产生的混沌序列具有很强的随机性。

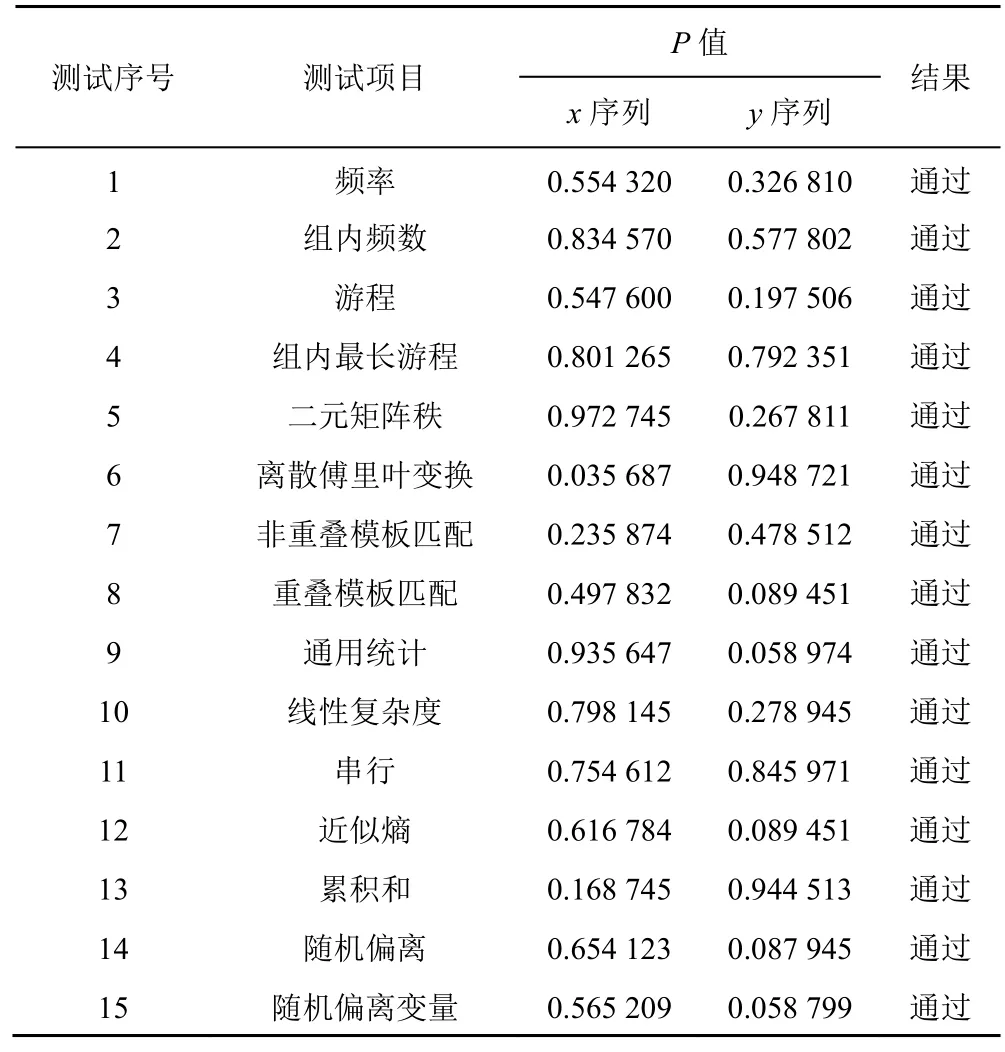
表2 混沌序列的NIST 测试结果

3 混沌映射在信息传输中的应用

由于混沌映射的不可预测性以及遍历性，因此其被广泛用于网络传输数据。利用混沌映射产生的序列进行数据传输时，其输出的分布对传输误码性能有很大的影响[26-29]。由于本文构造的二维多项式混沌映射的输出较为均匀地分布在整个取值空间上，因此使该混沌映射在安全通信中可以表现出较高的性能。本节使用参考调制差分混沌移位键控（RM-DCSK,reference-modulated differential chaos shift keying）[30]来演示本文所提混沌映射在信息传输中的性能。

3.1 RM-DCSK 通信方案

RM-DCSK 通信方案由发送端和接收端两部分组成。发送端首先利用混沌序列对信息比特位进行编码，生成传输信号，然后将传输信号发送给接收端。接收端对接收信号进行解码，从而恢复出信息比特位。

1) 发送端。传输信号的结构如图6 所示，b2k是第2k个信息比特位，Xk是一条长度为M的混沌序列，表达式为为扩频指数。RM-DCSK 通信方案的发送端结构如图7所示。首先，将系统的第一个时隙设置为参考时隙，混沌信号xi作为信息载波在第一个时隙内传输比特信息b2k，而第二个时隙是两部分之和，前一部分是将上一个时隙传输的信息作为信息载波，然后在第二个时隙内传输比特信息b2k1+，而后一部分是本时隙的混沌序列，即xi。则第k帧的传输信号si的表达式为

图6 传输信号的结构

图7 RM-DCSK 通信方案的发送端结构

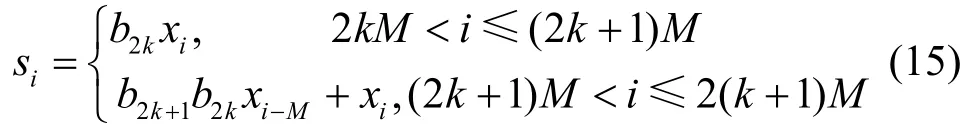
其中，混沌样点xi满足

2) 接收端。当接收端从发送端接收到传输信号时，可以利用相关器恢复原始信息比特位。RM-DCSK通信方案在解调时主要利用了混沌延迟特点和非相干技术，接收端结构如图8 所示。由于信号在不同网络中传输时可能会受到噪声的干扰，因此接收到的信号与原始信号有所不同。本文主要以加性白高斯噪声（AWGN，additive white Gaussian noise）信道模型作为主要通信传输媒介，信道中的干扰以加性白高斯噪声ξi为主，且则接收到的信号ri为

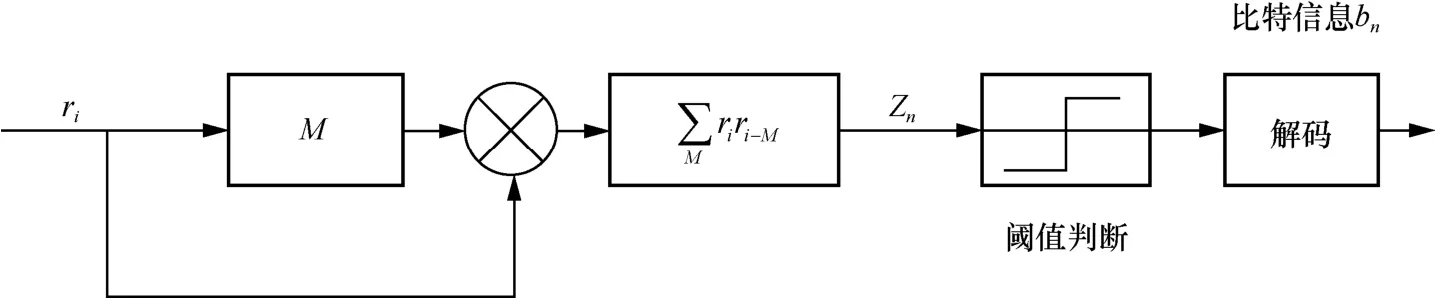
图8 RM-DCSK 方案的接收端结构

相关器Zn为

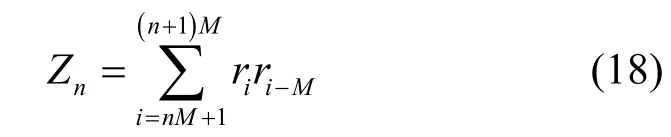
恢复出信息比特位b2k的相关器Z2k为

3.2 仿真实验

为了证明本文构造的混沌映射在RM-DCSK 中的优良特性，本文对比了现有的4 种二维离散混沌映射，如经典的Hénon混沌映射、2D-SLM、2D-LSMCM、文献[19]混沌映射。在不同的扩频指数M及不同等级噪声的AWGN 信道模型中，本文使用以上混沌序列发生器进行了RM-DCSK 通信方案的仿真。每次实验传输数据是一个随机生成的1×105bit 长度的二进制序列。通过计算接收到的数据与原始数据之间的误码率（BER,bit error ratio）来验证其抗噪声能力。第一组研究针对不同扩频指数下的误码率。对于每个混沌映射，实验设置如下。

1) 选取5 种混沌映射中的xn序列对信息比特进行编码。

2) 设置AWGN 通道的噪声强度为26 dB，在不同的扩频指数下，计算RM-DCSK 通信方案的误码率。

3) 在不同初始值下重复步骤1) 和步骤2) 10 次。

4) 计算这10 次实验误码率的平均值。

第二组研究针对不同噪声等级下的误码率。对于每个混沌映射，实验设置如下。

1) 选取5 种混沌映射中的xn序列对信息比特进行编码。

2)设置AWGN 通道的扩频指数M=80，在不同的噪声等级下，计算RM-DCSK 通信方案的误码率。

3) 在不同初始值下重复步骤1) 和步骤2) 10 次。

4) 计算这10 次实验误码率的平均值。

从图9 中可以看出，在不同扩频指数M下，RM-DCSK 通信采用本文提出的二维多项式混沌映射总能比其他混沌映射获得更小的误码率。从图10中可以看出，当信噪比较小时，使用不同混沌映射的RM-DCSK 通信方案可以获得几乎相同的误码率。但随着信噪比的增加，使用本文提出的二维多项式混沌映射比使用其他混沌映射可获得更小的误码率。这说明二维多项式混沌映射相较于其他混沌映射更适用于信息传输。

图9 不同扩频指数下RM-DCSK 方案的误码率

图10 不同噪声等级下RM-DCSK 方案的误码率

4 结束语

为了解决离散混沌映射存在着混沌范围不连续、输出分布不完整等缺陷，本文提出了广义二维多项式混沌映射，并通过理论分析与实验仿真证实了该映射的有效性，最后将5 种二维混沌映射应用于RM-DCSK 通信方案中。相较于其他混沌映射，本文提出的二维多项式混沌映射可以获得更小的误码率，说明了该映射更适用于信息传输。在后续工作中，本文将基于局域网，利用现场可编程门阵列硬件平台搭建通信方案模型，RM-DCSK 通信方案可以为加密端和解密端发送密钥。