一道二元最值问题的探究与拓展

甘肃省武威第八中学(733000) 王春梅

安振平老师在《中学生数学》2019年9月上半月课外练习高二栏目提供了这样一道题: 已知: x > 0, y > 0,3x2+y2=4.求的最小值.

多元最值问题历来是高考、高校自主招生和高校强基计划中的热点问题,上述问题是一道二元条件最值问题,以下笔者对这道试题进行解法探究、变式探究和拓展探究,以供同学们学习时参考.

1 解法探究

上述问题配套的参考答案中给出的是均值不等式法,特别巧妙地运用了两次四元均值不等式,在学习中发现同学们不易想到,下面给出另外五种解法.

1.1 待定系数均值不等式法

解法1(待定系数均值不等式法)设λ>0,由均值不等式可得,

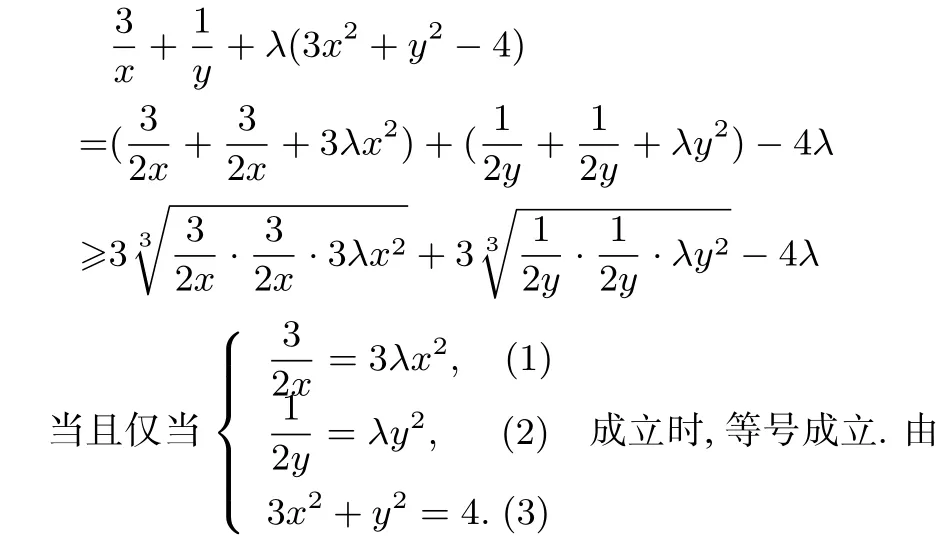
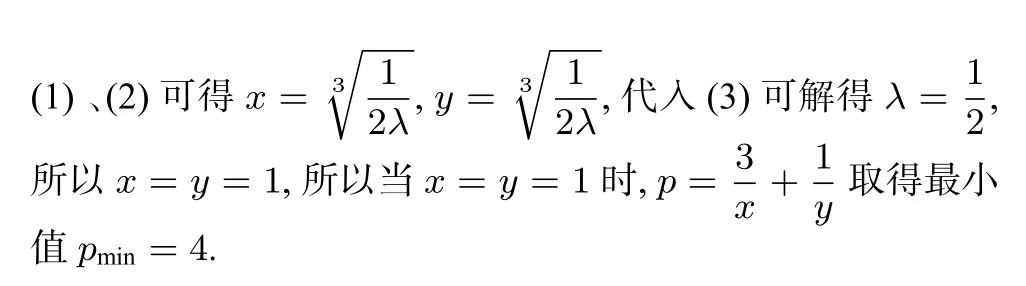
评注本解法引入大于0 的待定系数λ 后,运用了三次均值不等式和不等式的性质,联立均值不等式取等的条件和已知条件先后解出λ、x 和y 的值,最后代入求出p 的最小值.

1.2 三角换元法

评注抓住本题已知条件的结构特征,从形式上来看已知条件为带约束条件的焦点在y 轴上的椭圆的方程,联想到椭圆的参数方程,运用三角换元法把问题转化成关于α 分式型三角函数在给定开区间上的最值问题,利用导函数与函数单调性以及极值的关于,求出极值点,从而求出极小值也就是最小值,得出p 的最小值.

1.3 比值代换齐次化法

其中k >0,所以

令f′(k) = 0,可得k = 1,当0 < k < 1 时,f′(k) < 0,所以f(k) 在(0,1) 上单调递减, 当k > 1 时, f′(k) > 0,所以f(k) 在(1,+∞) 上单调递增, 所以f(k)min= f(1) =+7 = 16,即当x = y = 1 时,p2最小值为16,因为p>0,所以pmin=4.

评注比值换元后,题设中的双变量x 和y 实现了分离,再把待求式平方,把p2的最小值转化成求关于k 的函数在给定范围上的最值问题,发挥导函数的工具作用,利用导函数求出极值点,从而求出p2的最小值,从而得出p 的最小值.

1.4 权方和不等式法

1.5 赫尔德不等式法

解法5(赫尔德不等式法)因为x > 0,y > 0,由赫尔德不等式可得,

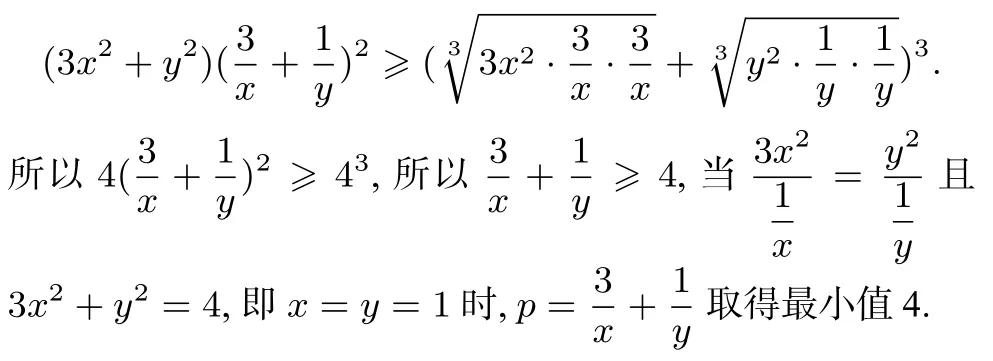
2 变式探究

将上述题目已知条件变为分式型, 待求式变为二次型,得到变式1:

将上述题已知条件变为一次型,待求式变为三次分式型得到变式2:

3 拓展探究