一个闭区间上的凸函数的最值问题的新角度研究

华南师范大学数学科学院(510631) 叶秀锦 刘润涛

利用函数的凹凸性证明不等式是一种比较常用的手段,也有较多的文章对此进行研究.绝大多数研究都是应用Jensen不等式研究上凸函数的最大值和下凸函数的最小值问题[1-2].而上凸函数求最小值,下凸函数求最大值问题研究甚少.本文探究上凸函数的最小值和下凸函数的最大值问题.

1 预备知识

引理1对于任意a≤x1≤x2≤x3≤x4≤b,x1+ x4= x2+ x3.若f(x)在[a,b]为下凸函数,则有:f (x1) + f (x4)≥f (x2) + f (x3).等号成立当且仅当x1= x2= x3= x4.

引理2对于任意a≤x1≤x2≤x3≤x4≤b,x1+ x4= x2+ x3.若f(x)在[a,b]为上凸函数,则有: f(x1) + f(x4)≤f(x2) + f(x3).等号成立当且仅当x1= x2= x3= x4.

引理1和引理3的证明见文献[3],引理2和引理4是引理1和引理3的对偶形式,类似可证.

2 本文结论及证明

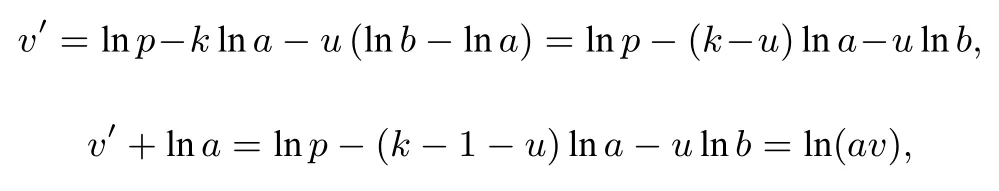
由引理3知:

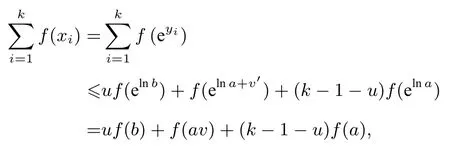
等号成立当且仅当yi(1≤i≤k)中有u个lnb, 1个ln(av),k-u-1个lna,即xi(1≤i≤k)中有u个b,1个av,k-u-1个a.

(2)是(1)的对偶形式,类似可证.

证明(2)是(1)的对偶形式, (4)是(3)的对偶形式,类似可证.下面仅证明(1)和(3).

(1) lnf (x)是下凸函数,由引理3,有:

(3) ln(-f (x))是下凸函数,由引理3,有:

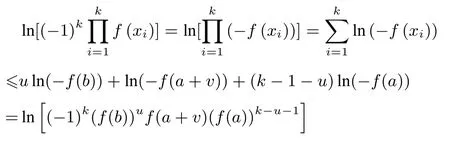
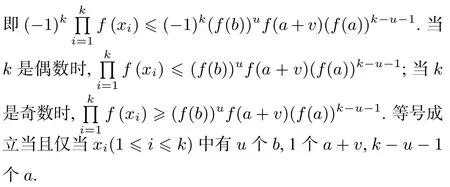
证明(2)是(1)的对偶形式, (4)是(3)的对偶形式,类似可证.下面仅证明(1)和(3).

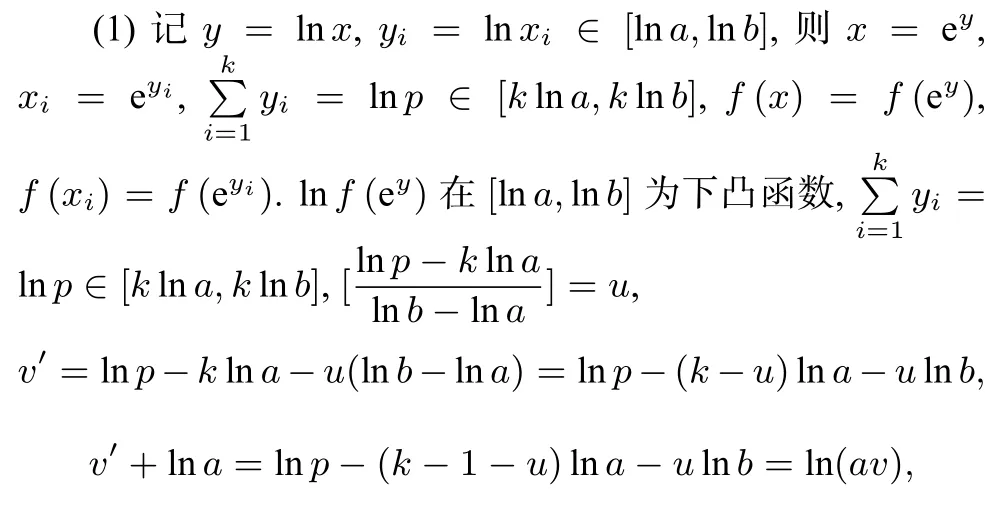
由引理3知:

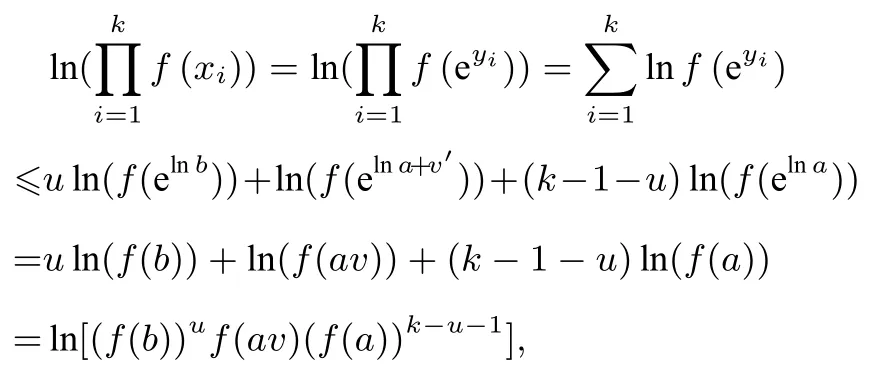
即

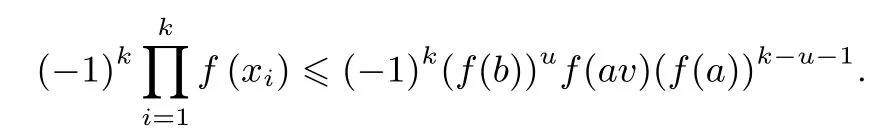
当k是偶数时,

当k是奇数时,

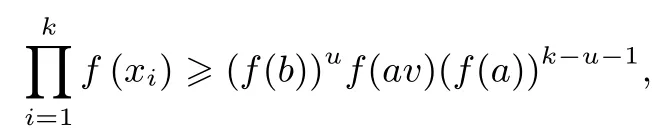
等号成立当且仅当xi(1≤i≤k)中有u个b, 1个av,k - u - 1个a.

3 定理的应用

应用定理1-3可以命制一些有难度较大的题目,比如,以下问题: