基于非线性系统正则标准形的三维路径跟踪问题

刘 伟

(江苏科技大学 自动化学院，镇江212100)

机器人的运动稳定控制中问题有两大类：轨迹跟踪和路径跟踪，两者最大的区别在于轨迹跟踪要求在某个时间到达轨迹上的某点，而路径跟踪不需要考虑时间上的限制[1].通常在实际情况中更多的使用路径跟踪算法.

对于路径跟踪问题，即是由适当的控制律将受控对象指引到目标路径曲线，并保持对象沿该曲线移动.而目标路径曲线通常是空间中的任意一条满足一定光滑条件的曲线.针对这一问题研究出许多有效的算法来解决路径跟随问题[2-3]，主要包括3类：① 利用人工向量场构造制导律，经典的方法有向量场法[4]；② 引入路径虚拟点，通过追踪虚拟点实现对给定路径的靠近和跟踪，例如纯追踪[5]和非线性导航法[6]；③ 将路径追踪问题转换为相对偏差系统的稳定问题，进而利用一些非线性理论中的常见方法实现稳定控制，例如滑模控制[7]，反步控制[8]，反馈线性化[9]等，实现路径的稳定追踪.受控对象的类型不同，例如轮式机器人[9]，水面舰艇[10]和水下机器人[11]，从不同的角度描述，数学模型也有不同，但控制策略和方法具有一定的通用性和借鉴性.

上述文献基本上都是研究平面上的路径跟踪问题，即二维路径跟踪.但实际上对于飞行和水下机器人更需要关注三维路径跟踪问题.文献[12]研究了恒定速度的无人机在三维空间中的路径跟踪，其设计的控制律是为了使对象的偏差和速度方向与指定曲线的偏差趋于零.因此，将路径跟随问题重新转换表述为一部分状态变量在零处的稳定问题[13]，然后，根据仿射系统的正则标准形，设计出反馈控制律，成功解决了这种状态稳定问题.

基于文献[12]中控制律的设计思想，文中研究无人机飞行变速时的三维路径跟踪问题.通过目标路径上的移动伴随坐标系，将惯性坐标系中的无人机运动系统转换为基于路径的偏差运动系统.再使用非线性系统的正则标准形推导出跟踪控制律.最后在仿真中验证了该运动控制律的有效性，无人机可以在变速度的情况下精确追踪曲线路径.

1 非线性系统的正则形式

为了得到合适的运动控制律，采用非线性系统f(x)=Ax+Bu的正则形式[14]：

(1)

式中：状态x=(x1,…xn)T∈Rn；输入u=(u1,…um)T∈Rm；A(x)=(a1(x),…,an(x))T；B(x)=(bij(x))n×m为n×m的矩阵，ai(x),bij(x)∈C∞(Ω)，i=1,2,…,n，j=1,2,…,m，Ω⊆Rn；系统输出y=h(x)=(h1(x),…,hm(x))T.

通过设计输入为：

将式(1)转换成如下关于状态变量Z的线性形式为：

使用线性系统理论中的标准方法就可得到新的控制输入ν1,ν2,…,νm，在平衡零点处镇定状态变量z.

2 无人机运动模型

文中将飞行空间中的无人机视为一个可控实质点，在惯性坐标系中使用以下6个变量来描述其运动的六维数学模型[15]：L为纵向距离，H为高度，Z为计算在右边的横向偏差，V为无人机速度的绝对大小，ϑ为航迹倾角，ψ为航迹偏向角.

(2)

式中：nx为纵向过载，沿着飞行速度方向；ny为横向或法向过载，垂直与飞行速度矢量；γ为过载向量侧倾角(滚转角)；g为重力加速度.由于过载能够表征可操纵力的大小和方向，而驾驶员一般就是通过改变该力的大小和方向来实现各种飞行器的机动动作，因此可以利用过载的概念来研究无人机的机动性[16].文中将nx，ny，γ视为控制量.对飞行器性能的约束通常由飞行器的飞行包线和过载极曲线得到.不同种类和型号的飞行器飞行性能差别很大.文献[16]中设定，-1≤nx≤1，-5≤ny≤5，-85°≤γ≤85°.

在式(2)中引入3个虚拟控制ν1=nx，ν2=nycosγ和ν3=nysinγ，则系统变为控制的仿射系统：

(3)

由系统(3)可知：ν1控制速度大小的变化，ν2和ν3控制速度矢量方向.

由于设计出的控制算法是要使得无人机能够沿着目标曲线移动，换个角度来说，控制的目标是要尽可能使得无人机与目标曲线间的偏差为零，因此可以不在惯性坐标系中，而是在基于路径的移动伴随坐标系中来描述无人机运动，即无人机相对目标曲线的偏差变化，基于追踪路径，提出了三维路径坐标.

3 变速度情况下的控制律设计

3.1 Bishop坐标系

路径伴随坐标系：设p(s)为给定路径；s为自然参数，文中s选用曲线弧长；q为无人机的当前位置.选择在参考路径上最接近q的点p0.并假定自然参数值s*对应于该点，即p0=p(s*).通常，最近点p0为唯一点，可以通过数值方法解出.所以点q位于与向量τ=dp/ds正交的平面π中，向量τ是最近点p(s*)在路径上的切向量.在π平面上选择一个平面坐标系n1和n2，则点q在n1和n2向量上坐标分别为d1和d2.

位于点p0处的3个单位向量τ，n1和n2就组成R3空间的坐标系，即为路径伴随坐标系.相对于惯性坐标系的转换矩阵为U(s)=(τ，n1，n2)，它的确定则取决于参数s.在以前的路径跟踪文献中，路径伴随坐标系较多地使用了Frenet坐标系，其公式为：

(4)

式中：τ,n和b分别是切线向量，主法向量和次法向量；k和κ分别曲线曲率和挠率.

但是Frenet坐标系的使用有一些限制，例如，曲率必需存在，不能为零；对于曲线路径，在弯曲部分主法向的方向通常会剧烈变化[17].考虑无人机飞行特性，文中采用Bishop frame坐标系[18].

其运动特征为：

(5)

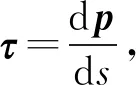
根据Frenet和Bishop坐标系的定义，两者之间的关系描述如下：

n=cosθFn1+sinθFn2

b=-sinθFn2+cosθFn2

式中：cosθF=k1/k，sinθF=k2/k.因此Bishop坐标系可以由Frenet坐标系通过绕向量τ旋转角度θF得到.但是通过θF角旋转，计算Bishop坐标系时，还是需要先计算出Frenet坐标系.这就仍然要面对Frenet坐标系的缺点.

Bishop坐标系沿曲线的变化可以看作是一个固连在该坐标系上的刚体的旋转，于是向量n1的动态变化[12]为：

(6)

使用数值积分方法，通过已知的向量n1的初值n1(s0)，就能计算得出任意n1(s).再由n2=τ×n1得到向量n2(s)，从而得到Bishop坐标系{τ,n1,n2}.

3.2 基于Bishop坐标系的路径坐标系统

基于惯性坐标系和路径伴随坐标系，无人机的位置q描述：

q=p+U(s)d

式中：d=(0,d1,d2)T表示无人机在Bishop坐标系中的位置，即无人机相对给定路径的偏差.

该方程对时间微分，得：

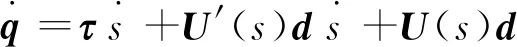
代入转换矩阵U(s)，展开合并后得：

写成矩阵相乘形式，可得：

通过标量积，将上述方程拆分整理为：

在此基础上加上速度V，状态ϑ和ψ的变化方程，由式(3)变换成描述无人机运动的新方程为：

(7)

该系统也是仿射的.

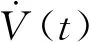
(8)

与此同时，已知q=(L,H,Z)，并且

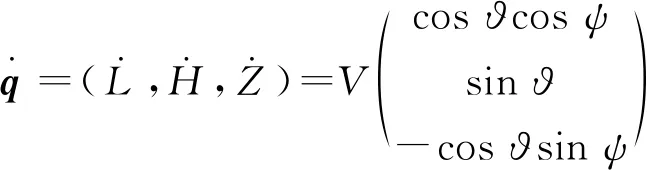
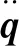
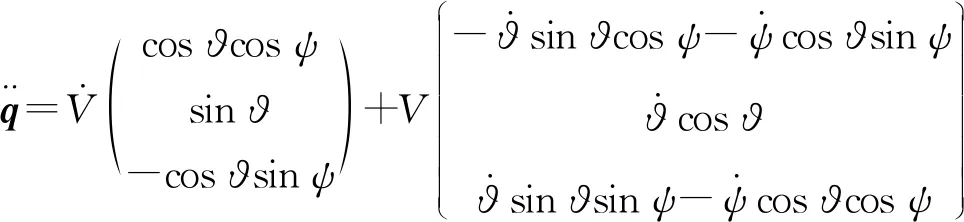
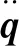
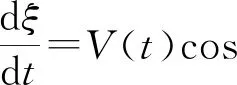
通过变换自变量，将式(8)写成另一种形式：

(9)

并且无人机位置向量经过变换，可得：

因此，q′再次微分得到：

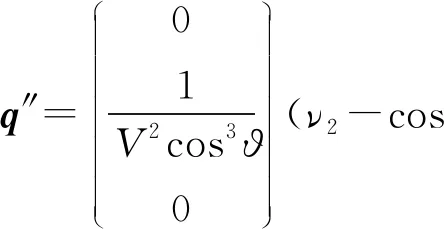
为了得到反馈控制律，对d′1和d′2再次微分，得：

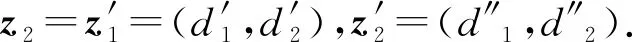
(10)

式中：

式(10)中的子系统z″1=P+Qν可以使用非线性稳定方法稳定.选择控制ν使得方程z″1=P+Qν转换为方程z″1+K1z′1+K2z1=0.为了确保系统的渐近稳定性，参数矩阵K1=λ1E和K2=λ2E，其中E为单位矩阵，参数λ1和λ2满足条件：二次方程σ2+λ1σ+λ2=0具有实数正根.于是得到了虚拟控制ν来稳定变量d1,d2,d′1,d′2:

ν=-Q-1(P+K1z′1+K2z1)

(11)

式(10)的另一个变量s.当‖z(t)‖→0时，变量s的状态由零动态方程决定.而

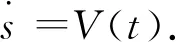
综上，在一定条件下可以实现无人机变速度情况下的路径追踪，即沿着目标曲线以速度V(t)运动.

4 仿真结果

基于文中控制律式(11)，检验无人机的路径跟踪效果.Matlab仿真实验中给定路径为直线：起点(0,0,0)，终点(100 m,100 m,100 m).无人机的初始状态(L0，H0，Z0，ϑ0，ψ0)=(10 m,20 m,10 m,0,0).速度值V(t)=15+3sin(t)(m/s).文献[21]中将前视法推广到了三维空间的路径跟踪，前视方法中有4个参数kϑ,kψ,δy,δz需要调节.而文中只用到两个参数λ1和λ2就可以调节跟踪效果.本节中，选择两种方法各自跟踪效果都较优的参数.前视方法参数[21]：kϑ=10，kψ=10，δy=10，δz=10；基于Bishop坐标系的反馈控制参数λ1=0.75，λ2=0.135.两种方法的路径跟踪如图1，2.

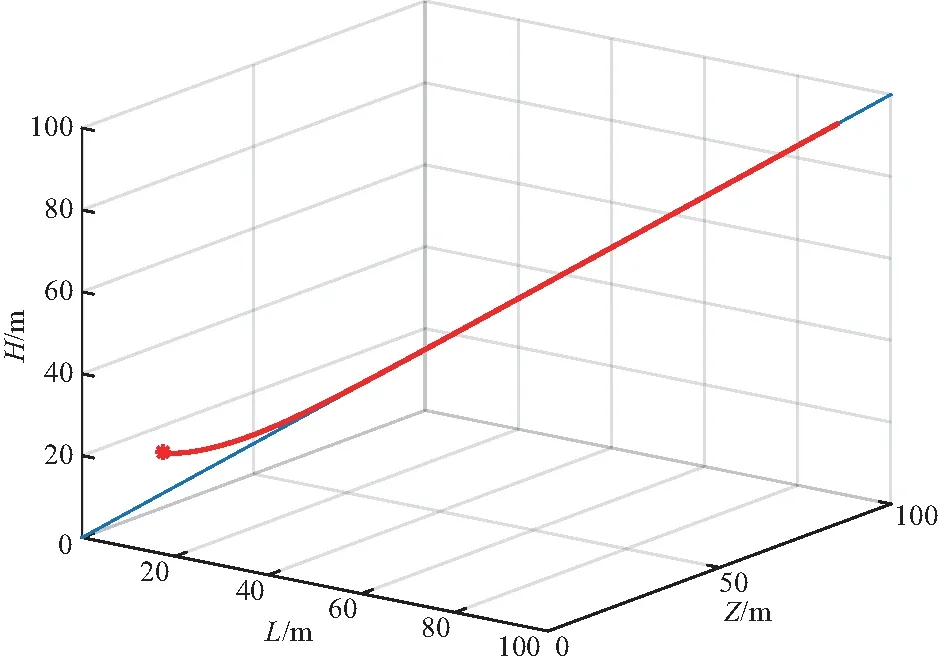
图1 基于前视法的无人机路径跟踪

从图1和图2中可以发现，基于前视法和基于Bishop坐标系的控制方法，无人机都能较好跟踪给定直线，无人机从初始点出发直接靠近并追踪给定路径，如图2.

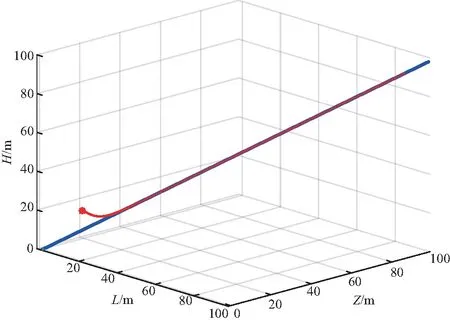
图2 基于Bishop的无人机路径跟踪

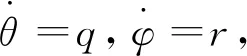
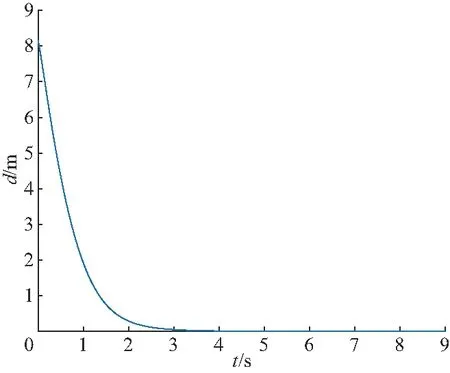
图3 基于前视法的无人机偏差距离d的变化

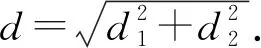
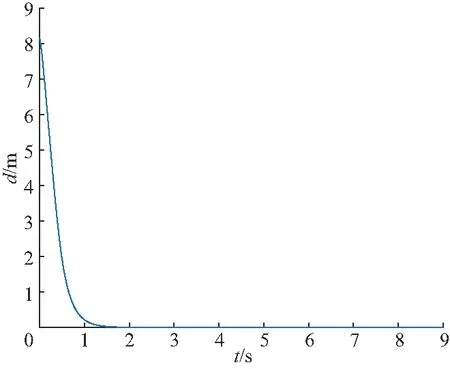
图4 基于Bishop的无人机偏差距离d的变化

5 结论

(1) 基于移动路径坐标系，通过路径坐标将三维路径追踪问题转换为关于相对偏差动力系统的稳定问题.再将该系统化为非线性系统的正则标准形，从而较容易地得到相应的系统稳定控制律.

(2) 针对无人机飞行速度大小变化且没有提前已知的情况，采用了自变量变换的方法，从而得到新的偏差系统方程.

(3) 经过仿真实验，验证了该控制律的正确与良好性，能够实现在变速度的情况下控制无人机路径追踪.下一步就是将该方法在半实物仿真平台中及实物平台中实现，并同其他方法进行比较.