可调共振型超表面对透射声波的三维波前调控
2022-10-09陈阿丽杜兴岳王昊煜
陈阿丽, 杜兴岳, 王昊煜
(北京交通大学 力学系, 北京 100044)
波动现象是自然界中一种常见的物质运动与能量传输的形式,一直以来都备受学者们关注,实现对光波、电磁波、声波和弹性波等的灵活操控是科学家和工程师们的研究热点之一。学者们提出并设计了一系列的超构材料如光子晶体[1-2]、声子晶体[3]、超材料[4]和超表面[5-6],通过对结构进行人工设计来实现对波传播性质的调控。光子晶体和声子晶体主要是通过设计结构的周期性来对光波和声波的能带结构进行调控。超材料的物理性质主要取决于其微结构单元,通过设计不同的构型可以获得不同的材料性能,并实现许多反常的物理现象和效应,如异常折反射、超透镜、非对称传输、反向多普勒频移等[7-9]。超表面是一种具有亚波长厚度子结构的二维超材料,具有结构简单、体积小和易加工的特点。一经提出便受到研究者们的青睐,最早用于电磁波领域,Li等[10]将超表面概念推广到声学领域,设计了超薄的反射型声学超表面,实现了异常反射、声波聚焦等多种声学功能。之后,声学超表面被广泛用于调控声波,主要有透射型、反射型和吸收型[6],按其单元的结构形式也可主要分为空间折叠型[10-13]、共振型[14-16]和薄膜型[17-19]等。
利用上述声学超表面实现了多种多样新奇的声学功能如异常折反射、聚焦、波束自弯曲、声源幻象、声波涡旋和全息等。但大多数已有的声学超表面一经加工制造,其所实现的功能和适应的工作频率便不能更改,这极大程度上限制了超表面的实际应用。可调声学超表面[20]的出现,一定程度上打破了这个局限性。总体来说,可调性可通过3种方式实现:1)设计机械可重构的单胞[21-25];2)调整超表面整体方位[26-28];3)利用压电、压磁等智能材料设计单胞或结构,通过外加偏场进行调控[29-32]。可调声学超表面实现了多功能性和宽频的特点,使波场的调控更加灵活,也提高了超表面的适用性。但目前相关研究还比较有限,可重构或可调的胞元形式还比缺乏。基于此,本文设计了有开口的可重构共振筒单胞,通过简单的旋转操作改变开口的大小进而改变单胞的共振特性,从而实现对透射声波的相位调节。基于广义Snell定律[33],利用此可重构单胞构建超表面对声波进行三维波前调控,实现了透射声波的异常折射、空间任意一点聚焦和波束自弯曲。
1 可重构单胞
超表面功能的实现依赖于其功能单胞对相位和透射率的调控能力,因此本文首先设计单胞并验证其调控能力。如图1所示,是设计的可重构共振筒单胞模型,主要有内筒和外部套筒组成。内筒是空心圆柱体,由5个横隔板将其分成了6层,即将单胞分成了6个空气腔。每层侧壁上有4个关于中心轴对称的开口,开口对应圆心角为45°。外部套筒内侧的薄壁套筒内径与内筒的外径相同,并且其上分布有与内筒完全相同的开口,通过旋转即可改变内筒开口的大小。当内筒的开口与套筒完全重合时整个共振筒结构对应的开口角度α=45°,开口完全错开时整个共振筒结构对应的开口角度为α=0°。为方便实际操作最外侧的薄壁筒通过4个竖隔板与内部的薄壁套筒相连接。单胞的几何尺寸为:外筒厚度为t=1 mm,直径为D=29 mm,筒高为H=43 mm,薄壁套筒厚度t2=0.5 mm,内筒直径为d=10 mm,厚t3=0.5 mm,横隔板厚度为t=1 mm,6个共振腔高度均为h=6 mm,开口高度为h1,外筒与套筒之间空气腔的厚度为T=3.5 mm,竖隔板厚度为t1=0.8 mm。
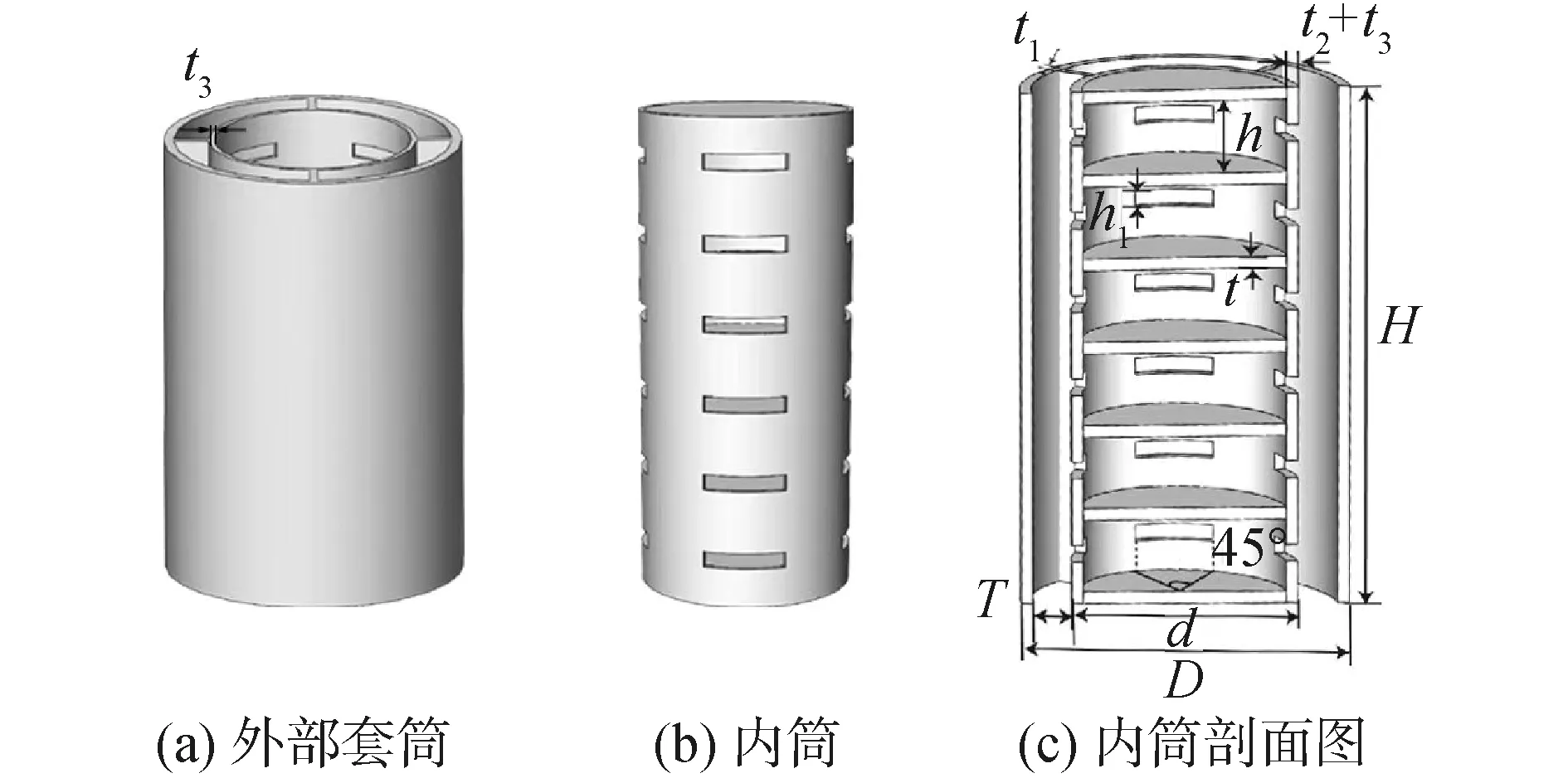
图1 可重构单胞示意Fig.1 The diagram of the reconfigurable unit cell
单胞模型确定后,即可利用有限元软件Comsol Multiphysics检验其对透射波相位和幅值的调控能力。如不特殊说明,本文以工作频率f=3 700 Hz为例来验证设计的单胞和超表面的性能。图2给出了此频率下透射波相位和幅值随可重构单胞开口角度的变化曲线。可以看出,随着开口角度的变化,透射波的相位变化覆盖了一个完整的2π范围,这确保了后续超表面可以对声波进行灵活的波前调控。从图2(b)可以看出透射率也随着开口角度的变化而改变,开口角度小于3°或者大于20°时都具有较高的透射率。后续依据广义Snell定律进行超表面设计时,在满足相位要求的同时还需考虑声波的透射率,尽量避免选择透射率较低的单胞。
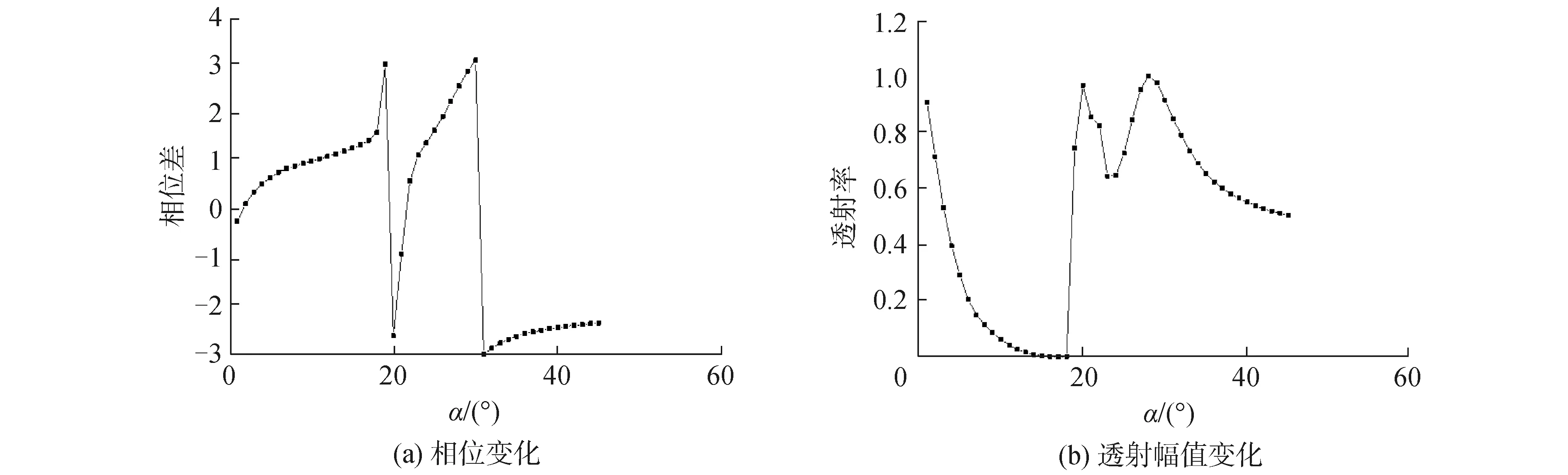
图2 单胞对声波相位和幅值的调节Fig.2 Modulation of phase and transmittance of the acoustic wave by the unit cell
2 三维广义Snell定律
超表面通过设计其亚波长结构,在声波的传播路径中引入相位改变进而对声波进行波前调控,这使得传统的Snell定律不再适用。Yu等[33]基于费马原理首先在光学领域提出了广义Snell定律。Aieta等[34-35]考虑了光波的平面外反射和折射,利用费马原理推导出了调节三维光波波场的广义Snell定律。Li等[36]推导了三维声波波场满足的广义Snell定律,并设计可调超表面对反射声波进行了面外调控。如图3所示,假设入射声波位于xoz平面,则调控透射声波和反射声波的三维广义Snell定律可分别表示为:
(1)
式中:θ为声波与其在yoz平面上的投影之间的角度;φ为声波在yoz平面的投影与z轴之间的角度;下角标i、t和r分别对应入射波、折射波和反射波;入射声波位于xoz平面故φi=0;φ(x,y)为超表面的相位分布函数,可依据设定的功能和工作频率来确定。本文主要实现了声波异常折射、聚焦和自弯曲功能,利用式(1)的第1个式子,可分别给出所需的超表面相位分布函数的表达式。
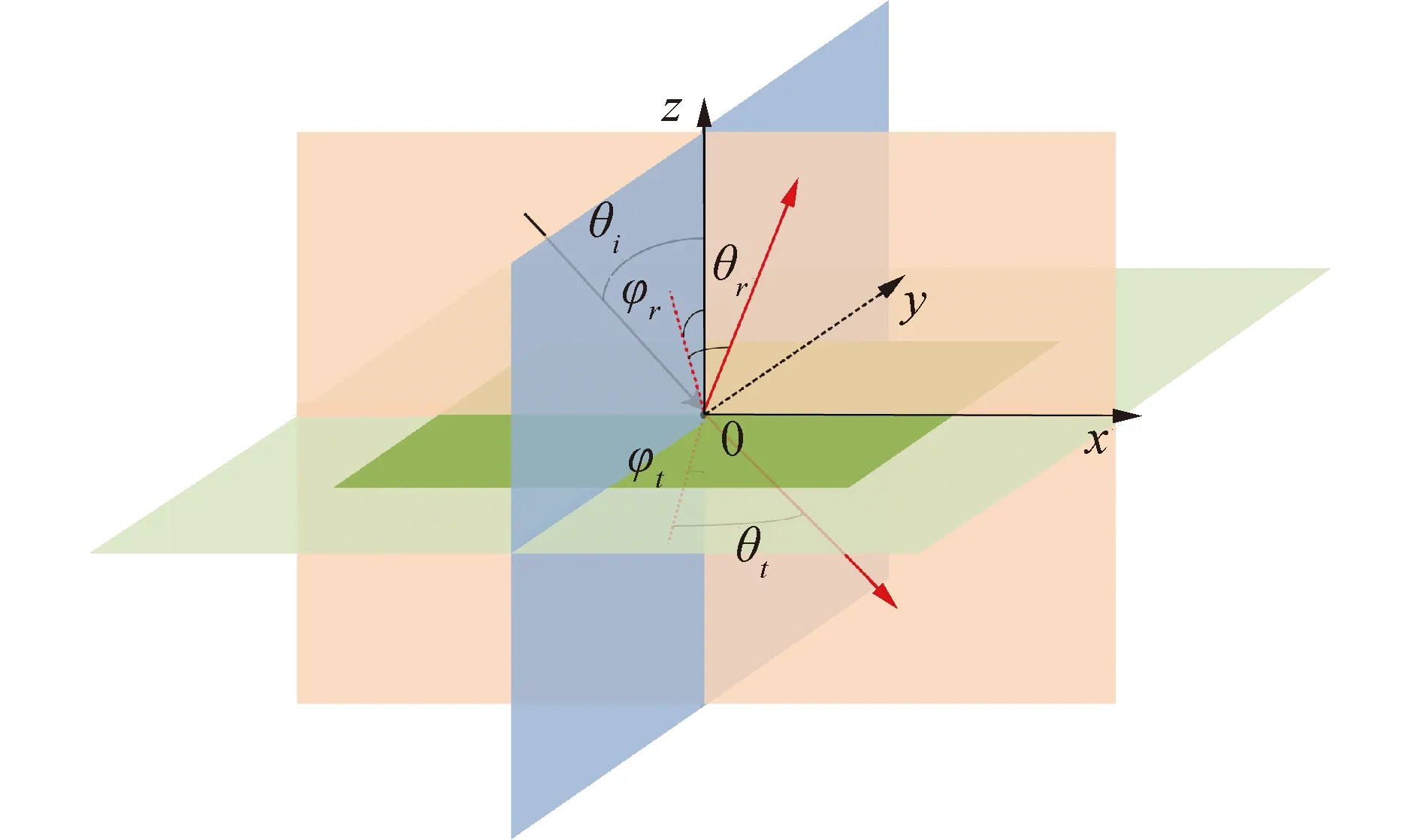
图3 三维广义Snell定律示意Fig.3 The schematic diagram of the 3D-Generalized Snell′s law
异常折射功能可调控透射声波沿空间任意方向传播,是超表面实现其他复杂功能的基础。超表面实现异常折射功能时的相位分布函数为:
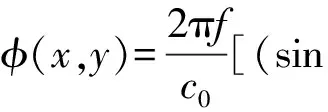
(2)
式中:Φ0为初始相位;c0=343 m/s为空气中声波的波速。
波束聚焦功能使透射声波的能量聚集到空间任一点F(x0,y0,z0),此时超表面的相位分布函数为:
(3)
任意一个与xoy平面垂直的平面内,波束自弯曲功能可使入射平面波转变为沿曲线路径r=g(z)传播的非衍射波束,并且具有绕过障碍物后还可以沿原路径传播的自愈合功能[37],此时超表面的相位分布函数为:
(4)
式中:z=h(r)为r=g(z)的反函数。空间的波束自弯曲可以看作是由超表面上每一点透射的声束组成的包络面。本文所讨论的包络面为球面的一部分,其轨迹为x2+y2+z2=R2的一部分,R为球的半径,代入式(4)可以得到此时超表面上的相位分布函数:
(5)
3 超表面及其功能实现
利用上节得到的不同功能对应的相位分布函数,结合图2可以确定超表面上每一个单胞对应的开口角度,即可完成超表面的设计。通过调整各个单胞的开口角度即可实现超表面的重构,进而实现不同声学功能或者不同工作频率之间的切换。本节利用有限元软件Comsol Multiphysics数值上实现了声波的三维异常折射、聚焦和自弯曲功能。
平板状超表面如图4(a)所示,xoy平面内的超表面在x和y方向上各有11个单胞,一共121个单胞,每个单胞与其相邻单胞之间的圆心距为40 mm;超表面长和宽均为480 mm,超表面厚度H=43 mm。声学通道有限元模型如图4(b)所示,以超表面上表面的中心为坐标原点,坐标系如图中所示。为了方便观察透射场信息,将入射场设置在超表面下方,在模型最下层施加沿z轴负向的平面波面声源,声压幅值为1 Pa;模型四周和上下表面施加平面波辐射条件来减少反射声波的影响。超表面的材料为聚氯乙烯(PVC),其阻抗与空气中的声波相差较大,故模型与空气接触的界面均可当作硬边界,在有限元计算时不考虑流固耦合的作用。网格划分要确保计算结果收敛。
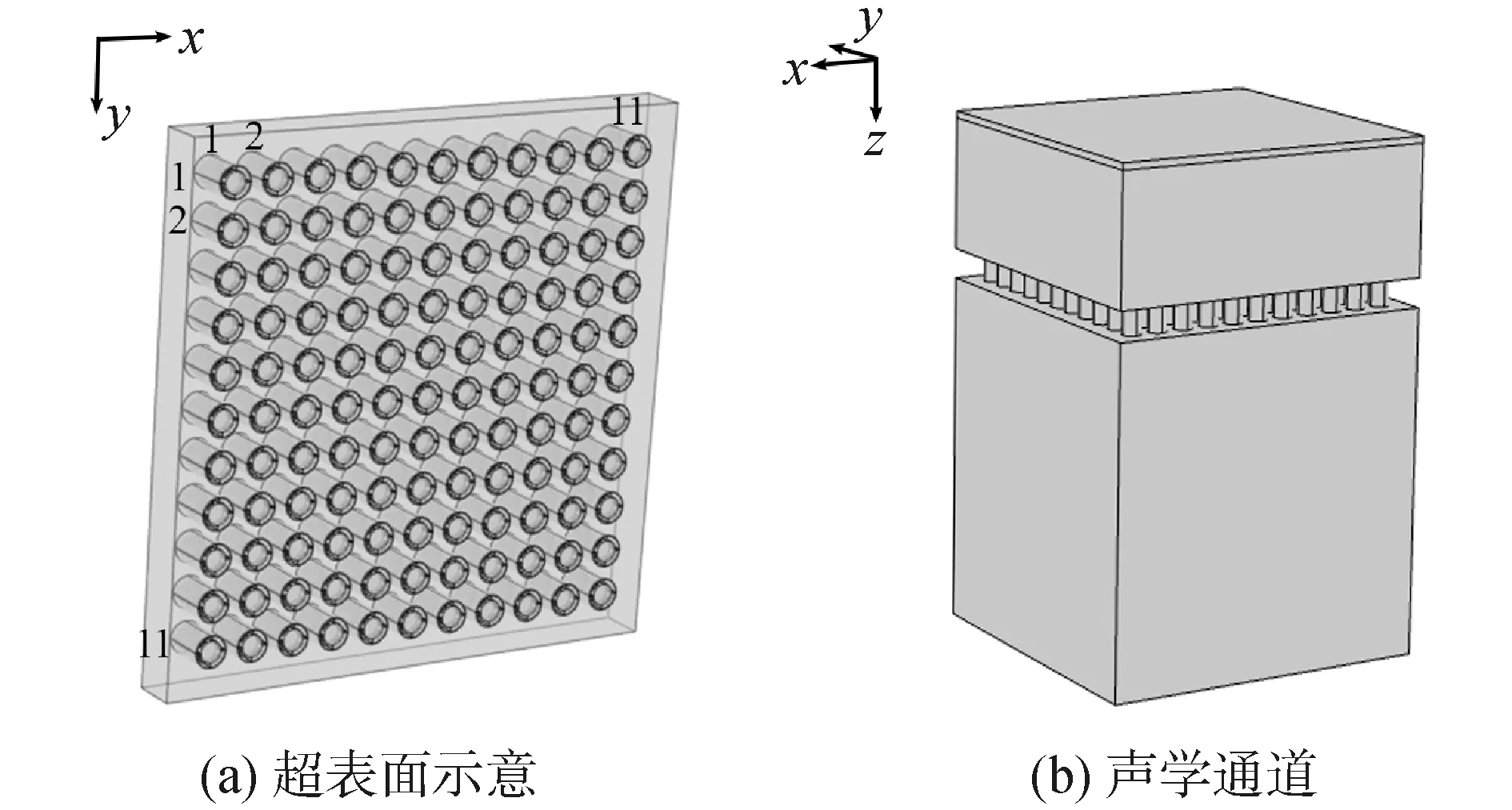
图4 超表面和声学通道的有限元模型Fig.4 Schematic diagram of a metasurface and acoustic channel model in Comsol
对于异常折射功能,给定θt和φt后,由图3可以计算出折射平面与入射平面xoz的夹角表达式β=arctan(cosθtsinφt/sinθt),在折射平面内,折射波与z轴的夹角可表示为γ=arccos(cosθtcosφt)。本文考虑入射角θi=22.5°,折射角θt=0,φt=60°和θt=60°,φt=30° 2种情况,第1种情况对应β=90°,γ=60°;第2种情况对应β=16.1°,γ=64.3°。超表面所需各单胞的开口角度分别见表1和表2,其中nx表示沿超表面x方向的单胞编号,ny表示沿超表面y方向的单胞编号。
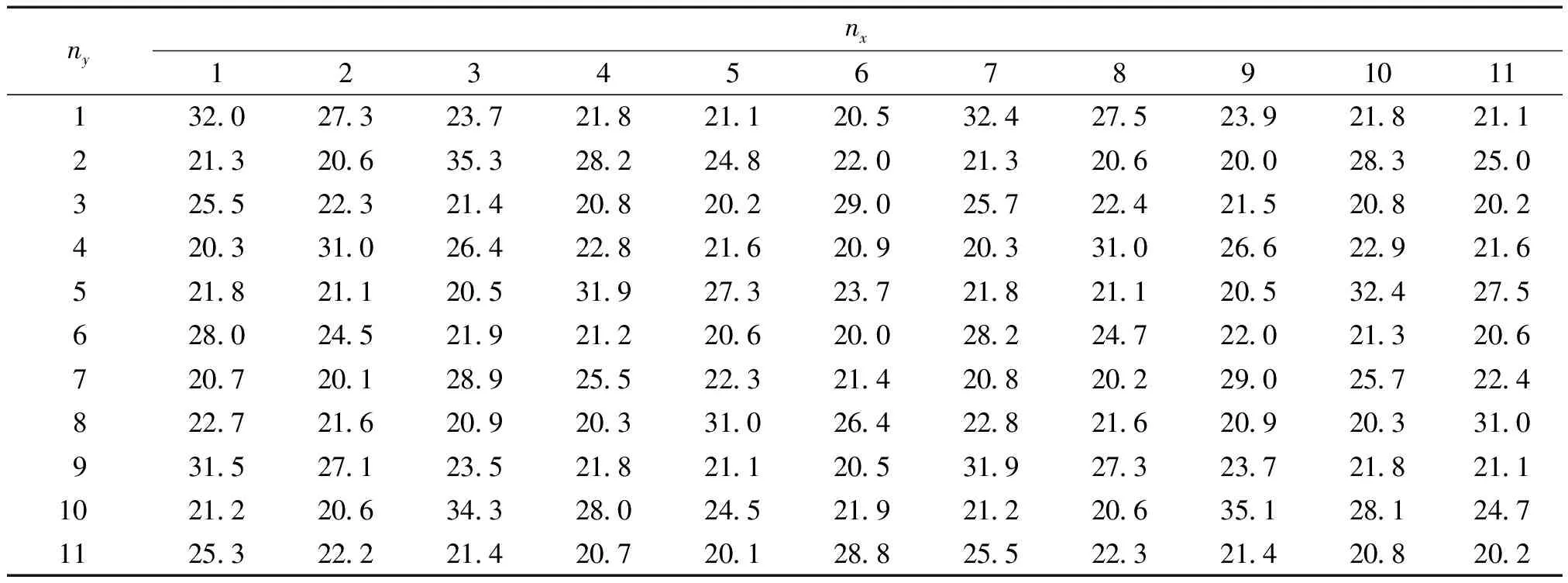
表1 异常折射功能(f=3700 Hz,θi=22.5°,θt=0,φt=60°)所需的各单胞开口度数Table1 The opening angles of each unit cell for abnormal refraction (f=3700 Hz,θi=22.5°,θt=0,φt=60°)
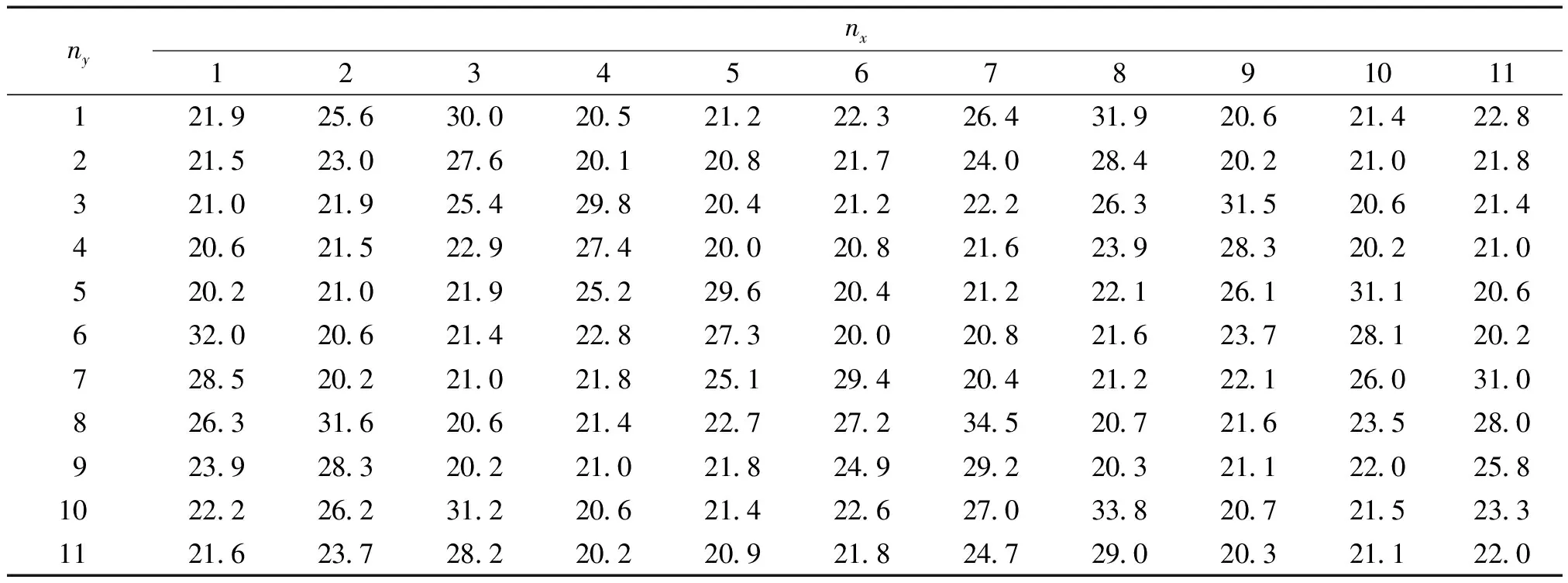
表2 异常折射功能(f=3700 Hz,θi=22.5°, θt=60°,φt=30°)所需的各单胞开口度数Table2 The opening angles of each unit cell for abnormal refraction (f=3700 Hz, θi=22.5°, θt=60°,φt=30°)
图5(a)和(b)分别给出了入射平面和折射平面内归一化声压场p/p0的模拟结果。为了显示地更清楚,图中选取的视角稍有差别。图中白色射线表示折射面内平面波的传播方向,其与z轴夹角与计算出来的2个γ值吻合。结果显示,经超表面调控后可在与入射面不同的平面内沿着预定方向传播,设计的超表面对波阵面的三维调控效果明显。
图6(a)和(b)分别模拟了超表面的中心聚焦和任意点聚焦功能,焦点分别设定为(0 mm, 0 mm, -200 mm)和(140 mm, -60 mm, -200 mm)。图中显示的是归一化之后的能量场(p/p0)2的分布,可以看出声波能量都聚集在设定的焦点处,焦点处的声场强度可以达到背景声场的35倍(中心聚焦情况)或25倍(任意点聚情况)左右。算例证明设计的超表面对不同位置的点聚焦都具有良好的效果。其中超表面所需各单胞的开口角度分别见表3和表4。
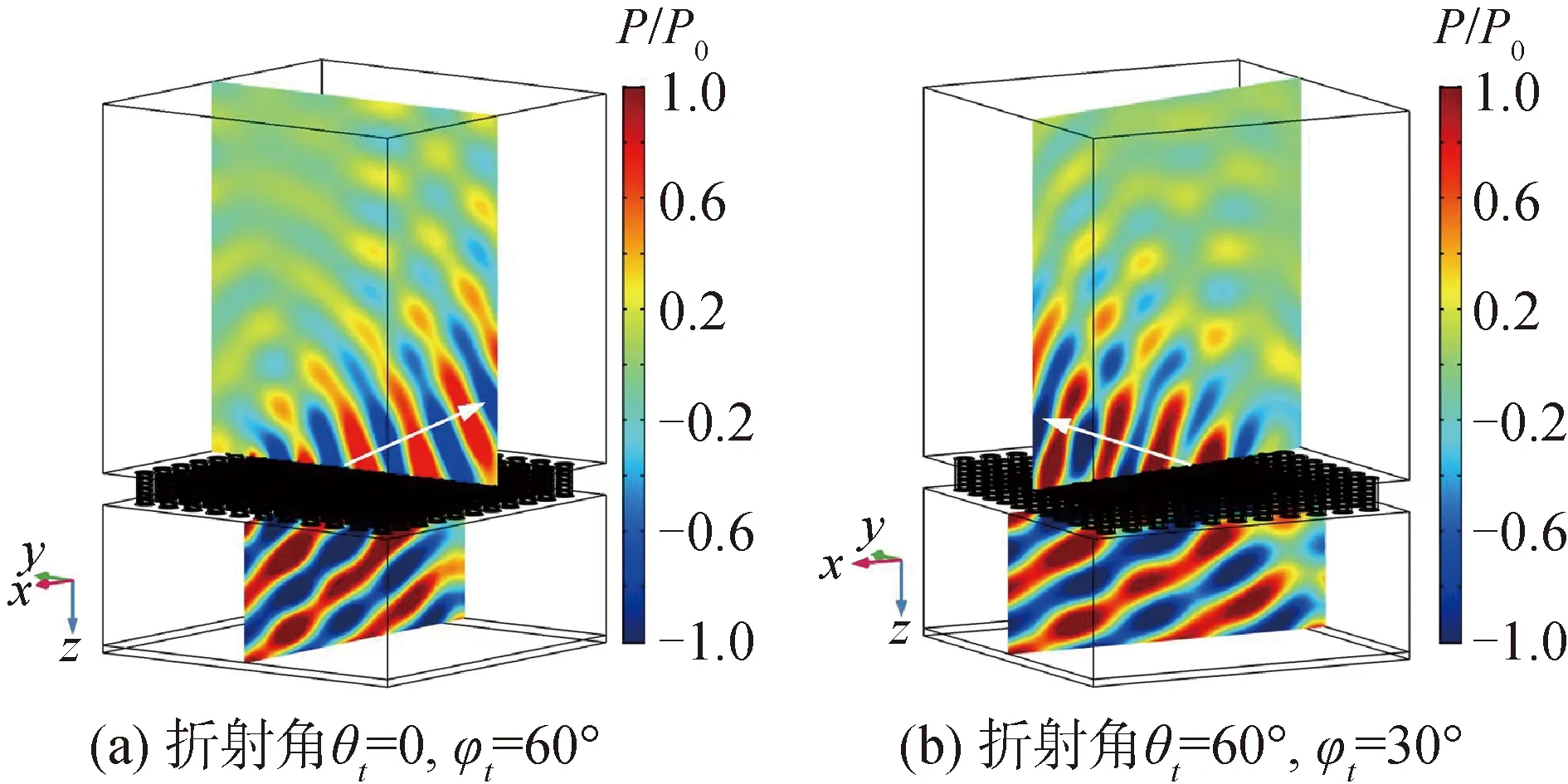
图5 入射角θi=22.5°时的异常折射功能Fig.5 Functionality of abnormal refraction in case ofθi=22.5°
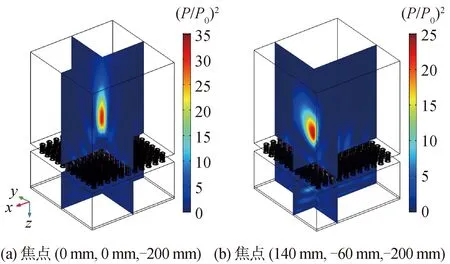
图6 聚焦功能Fig.6 Functionality of wave focusing
图7展示了超表面的波束自弯曲功能。图中选取了2个不同方位的平面来显示其空间自弯曲功能,白色虚线是设计的自弯曲轨迹。为了显示本文设计的可重构超表面也可在不同工作频率之间切换,这里选择了2个频率进行数值模拟。图7(a)对应的工作频率为3 700 Hz,球面半径R=150 mm;图7(b)对应的工作频率为3 400 Hz,球面半径R=250 mm。可以看出对于不同的工作频率和不同的球面半径,超表面都很好地实现了波束自弯曲功能,相比之下,设定的半径较大的时候,自弯曲的效果较好。其中超表面所需各单胞的开口角度分别见表5和表6。
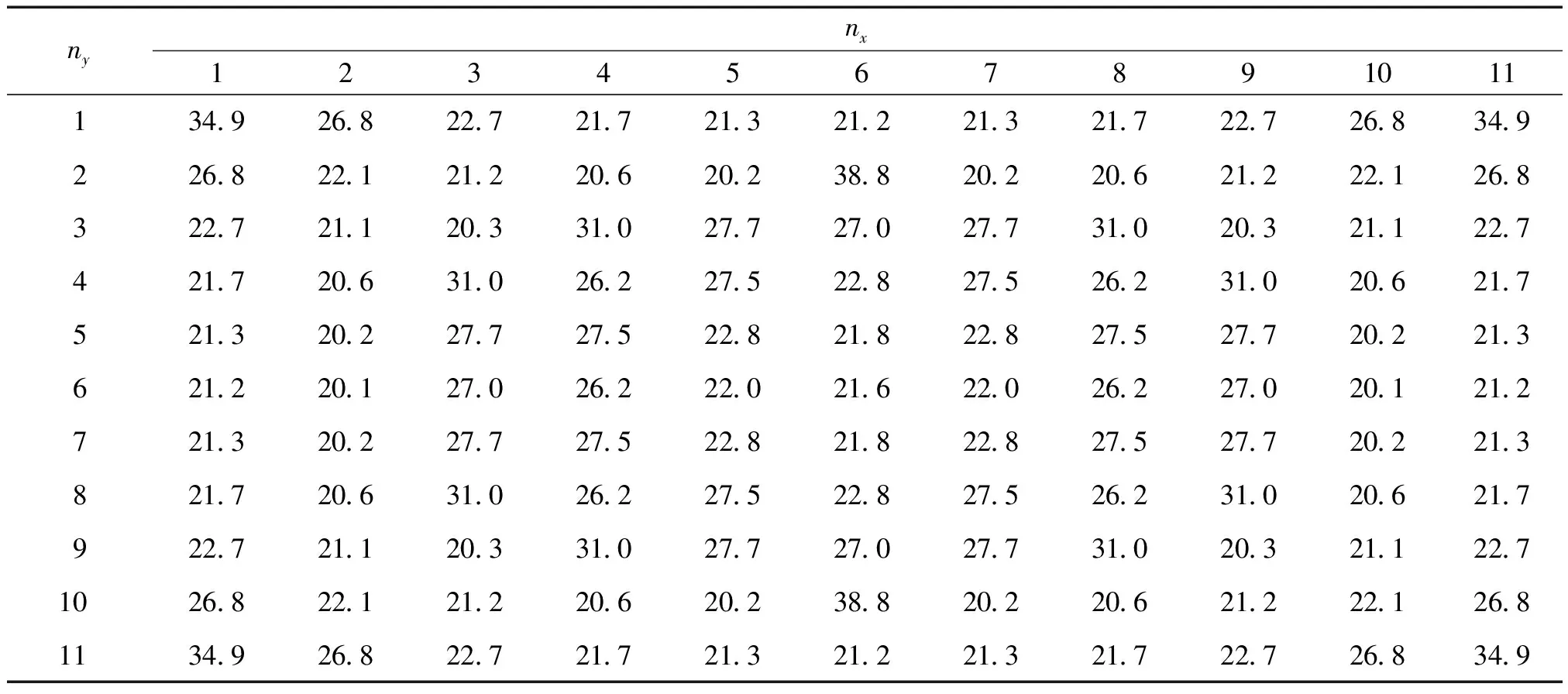
表3 f=3700 Hz, 焦点为(0 mm,0 mm,-200 mm)时点聚焦功能所需的各单胞开口度数Table3 The opening angles of each unit cell for wave focusing withf=3700 Hz and the focus being (0,0,-200 mm)
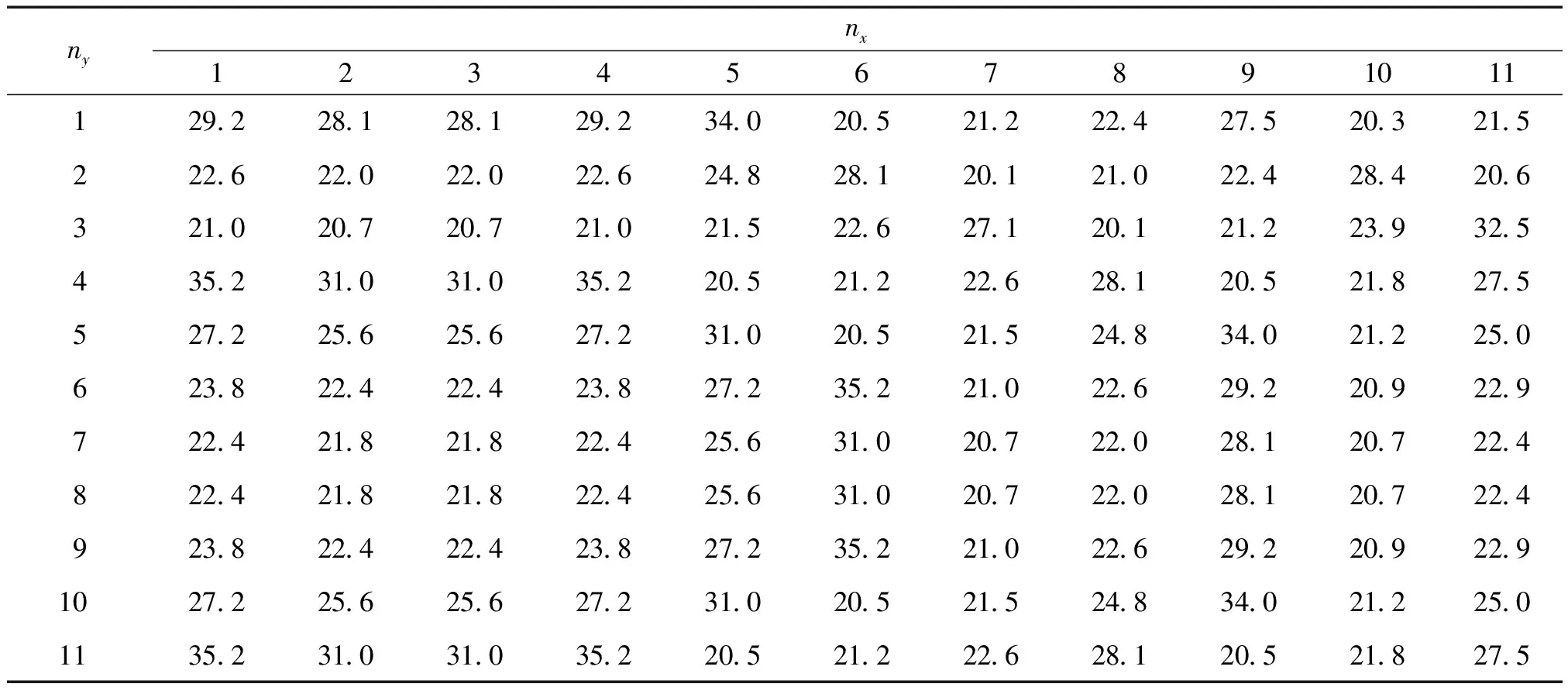
表4 f=3700 Hz, 焦点为(140 mm,-60 mm,-200 mm)时点聚焦功能所需的各单胞开口度数
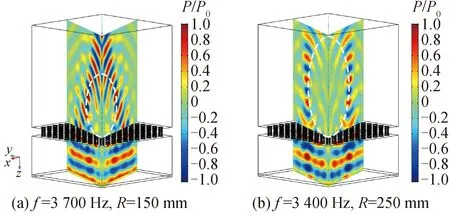
图7 波束自弯曲功能Fig.7 Functionality of wave self-bending
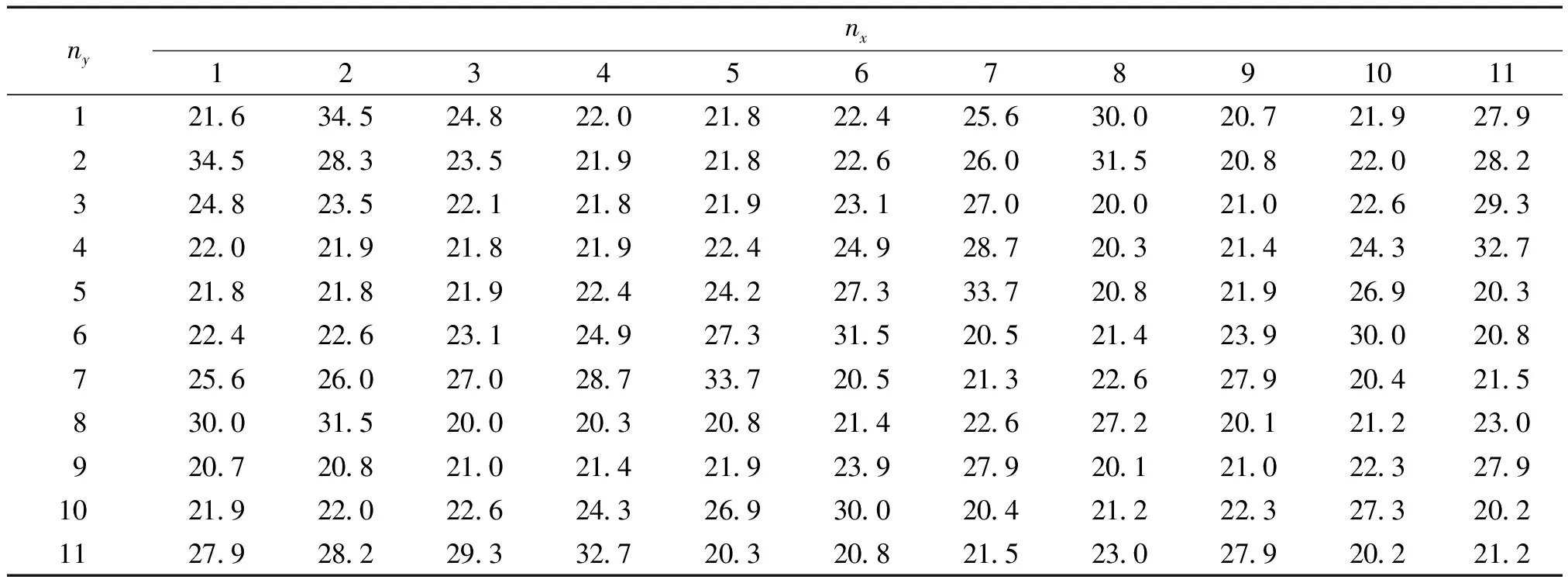
表5 f=3700 Hz,R=150 mm时波束自弯曲功能所需的各单胞开口度数Table5 The opening angles of each unit cell for wave self-bending withf=3700 Hz andR=150 mm
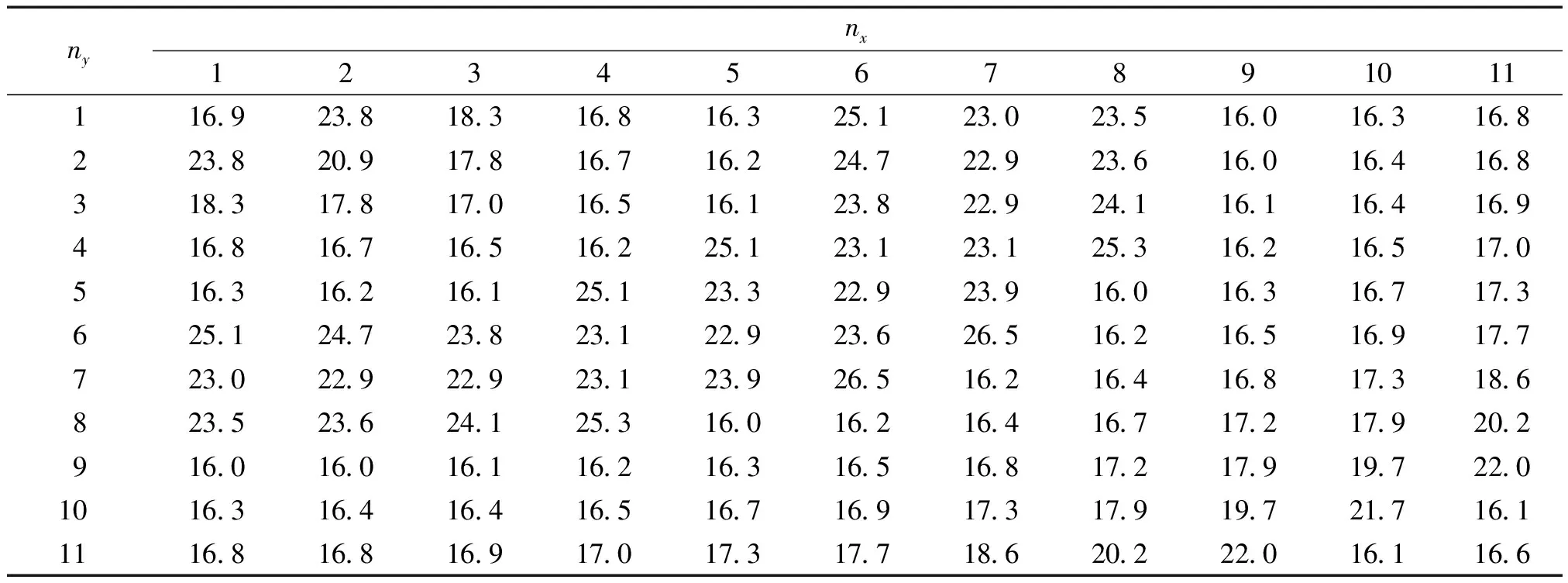
表6 f=3400 Hz,R=250 mm时波束自弯曲功能所需的各单胞开口度数Table6 The opening angles of each unit cell for wave self-bending withf=3400 Hz andR=250 mm
4 结论
1)设计了共振型可重构单胞,通过旋转改变开口角度的大小来改变单胞的共振性能,进而改变透射声波的相位。
2)利用有限元模拟验证了单胞对相位和透射率的调控能力,随着开口角度的变化,透射波的相位变化覆盖了一个完整的2π范围。有些开口角度下透射波幅值较低,构建超表面时尽量避免选用这些单胞。
3)基于广义Snell定律构建可调超表面对透射声波进行三维波前调控,在不重新加工制作超表面的前提下,仅通过调整各单胞的开口角度就实现了异常折射、聚焦和波束自弯曲功能之间的转换,同样也实现了不同工作频率之间的切换。
模拟结果显示设计的超表面很好地实现了既定功能,验证了设计的可调超表面的灵活性和有效性,后续可通过3D打印加工试件,并进行实验验证。本文的研究对新型声学器件的设计及声学超表面走向实际应用提供了一定的理论指导。
