高效非局部聚焦水声超表面

杨天， 杨天智

(东北大学 机械工程与自动化学院，辽宁 沈阳 110819)

超材料是一种具有亚波长单元尺寸结构的人工材料，拥有超越天然材料奇特物理性能。超材料的种类繁多且功能各异，常见的超材料包括光学超材料、热学超材料[1]、力学超材料[2-5]等。此外，在过去的10余年里，声学超材料的研究取得了重大进展[6-10]。其中，能产生相位突变的平面声学超材料被称为声学超表面。目前，基于广义斯奈尔定律[11]，通过采用不同相位调制方法设计的超表面已经实现了聚焦、宽带异常反射、自弯曲和声滤波等功能[12-14]。近年来，水下超材料声学技术得到了广泛的关注[15-19]。各种奇异的水下声学现象已经被陆续观察到，如波束分裂和非对称传输[20]、波束转向[21]、隐身地毯[22]、水下虹吸[23]和平面波转换[24]等。然而，在上述水声超表面的研究中，声波能量控制的效率始终不高，这始终受到2个主要因素的限制：宽带阻抗失配[25]和流固耦合作用[26]。对此，本文设计了一种具有非局部特性的新型声学超表面，能够有效地克服上述2种限制因素；结合优化设计算法，也可以进一步提高水声超表面的效率控制极限[20]。尽管现有的相关发现部分揭示了超材料的非局部特性能够有效地加强对声波的操纵，但目前的研究仅采用局部化的设计：超表面的微结构之间相互独立。尚无非局部水声超表面的相关研究发表。在这项工作中，本文提出了一种高效非局部聚焦水声超表面，它可以实现典型的声学聚焦功能。将传统局部水声超表面的独立谐振腔单元直接连接，获得具有耦合作用的非局部单胞。进一步地，根据广义斯奈尔定律，将非局部单胞对称地排列组合成高效非局部水声超表面。

1 理论依据

如图1所示，为了实现对水下平面声波聚焦的高效控制，在亚波长尺度上设计了一层具有相位梯度的对称性超表面结构，满足声波路径对相位突变的需求。根据广义斯奈尔定律可知，入射角与折射角之间的关系可以表示为:

(1)

式中:θi和θt分别代表声波的入射角和折射角；cw是声波在水下的传播速度，频率f0= 23.3 kHz，相应的波长为λ0=cw/f0；dφ(x)/dx是相位梯度相关项。

图1 水下声波聚焦的高效控制示意Fig.1 Schematic diagram of efficient control of underwater acoustic focusing

进一步地，为了实现将入射的平面波转化为球面波，超表面的周期性对称结构的相位补偿分布应服从依赖于空间位置的抛物线分布。如图1所示，每个功能单元由8个单胞组成。一般地，正向入射的超表面相位分布可由广义的斯奈尔定律推得[27]：

(2)

式中:kt是波矢量;PS是为了实现聚焦需要补偿的距离；λ0为波长;fx是沿x方向的焦距;y为沿y方向的尺寸；φ(y)为不同y方向位置所对应的相位大小。

值得注意的是，虽然每个谐振腔之间的耦合壁看起来与空气中的局部超表面的设计极为相似，但二者基本作用机制却明显不同：在水域环境下，由于流固耦合作用的效果极为明显，耦合壁显现出弹性体特质；而在空气中，流固耦合作用的效果极弱，耦合壁应被视为刚性结构。因此，水域中耦合壁将单胞内的独立单元格连接为一个整体，大大加强了水声超表面的长程相互作用，进而有效地提高了聚焦效率。

2 单胞的非局部设计

图2(a)所示，局部超表面的单胞是由3个尺寸相同的独立振动的亥姆霍兹谐振腔等间距纵向交错排列组成的。其中，每个单胞中的谐振器均可以看作一个单自由度的质量-弹簧系统。因此，局部超表面单胞内部的每个谐振腔的振动均是相互独立的。

图2 单胞模型对比Fig.2 Comparison of the unit cell models

通过直接耦合局部超表面单胞内的谐振腔，获得了非局部超表面单胞。相比之下，非局部超表面存在耦合壁，能量可以在相邻谐振腔之间穿梭交互。图2(a)显示了在x-y横截面上，声波沿x轴正向入射的情形。单条模型y方向的宽度为d。单胞的长度和宽度分别为a和b，谐振腔的深度和宽度为l和h，端口的深度和宽度为l0和h0。局部单胞中谐振腔之间的间隙表示为e，腔体壁厚为t。单胞的材料特性和详细几何参数分别列于表1和表2。通过调整l的大小可以实现系统的不同振动特性，覆盖2π全范围的相移。需要注意的是，为了满足超表面厚度的亚波长要求，尺寸a需小于超表面工作波长。

表1 材料属性Table1 Material properties

表2 几何参数Table2 Geometric parameters mm

为了得到可变参数与相移之间的关系，使用有限元软件COMSOL Multiphysics进行建模和模拟。考虑到流固耦合作用对相移的影响，使用COMSOL中声学-固体力学的频域模块，分别评估局部和非局部单胞的频响关系。首先构建一个带有单胞的超表面条形模型，如图2(a)中显示。将模型中在单胞左侧区域沿x方向施加的背景声压场作为初始入射波；在右侧区域距离单胞9b(b=30 mm)处放置探测点A，并检测该点处的声波相移；将连续周期性边界条件分别应用于单条模型的上下层边界；模型的左右两端均采用完美匹配层模拟无限边界(图中未显示)以吸收传输到边界的所有声波；使用物理场控制的自由三角形网格；采用扫掠网格对完美匹配层进行离散。

结果显示，当考虑流固耦合作用时，频率在21.3 kHz≤f0≤27 kHz内折射波相移随参数l的变化，几乎均可实现相位2π被完全覆盖。值得注意的是，局部单胞折射相移普遍突变明显且连续性差；相比之下，非局部超表面单胞具有更平滑的折射相移变化。这表明非局部水声超表面不但具有连续均匀的参数尺寸，而且对声波的操控能力更强。横纵对比的结果有力地说明了，非局部超表面离散相移时，对应的参数尺寸分布均匀，这对超表面的实际制造尤为重要；如图2(b)、(c)所示，非局部设计的透射率在全参数范围内均能保持高透射率。局部和非局部单胞的最小透射率为1.1%和77.3%，分别用紫色五星标记。此外，非局部水声超表面实现的聚焦效应对频率变化不敏感，在案例中，它接受的频率范围为[22.1，24.3]kHz。这意味着非局部设计不仅对微小的频率波动适应性更强，而且对制造误差的鲁棒性也优于传统的局部设计。

为了不失一般性，选择f=23.3 kHz的声波进行进一步的研究比较。如图2(b)、(c)所示，通过改变l的大小，几乎实现了[0, 2π]的相移，其中图(c)所示实线变化更加均匀。这意味着随着l的调整，非局部设计比局部设计具有更均匀更缓和的相移。此外，局部设计的透射率随着参数变化急剧下降至1.1%，这也是严重限制局部超表面聚焦效率的重要因素之一。

3 算例分析

为了对比局部超表面和非局部超表面对声波聚焦操控的效果，将y=0处的焦距fx定义为波长的6.5倍(即：fx=6.5λ0)，其中，y方向的不同位置所对应的相位大小φ(y)可根据式(2)计算得出。进一步地，分别参考图2(b)、(c)中的2条相移曲线(实线)，取离散相位所对应的参数值构建局部和非局部水声超表面，变量参数l如表3所示。

表3 中心聚焦的参数变化Table3 Variable parameters of central focusing mm

如图3(a)、(b)所示，在正入射(θi=0°)的背景声压场(P0=1 Pa)作用下，聚焦声压场的模拟结果(入射声压场未在图中显示)。图中白色虚线的交点为聚焦点。不难看出，非局部设计比局部设计的聚焦操控效果更好。如图3(c)、(d)所示，为了定量地描述局部和非局部超表面的聚焦效果，分别绘制了x=0.418 m和y=0处的聚焦声压场分布曲线图，以精确比较二者聚焦性能的优劣。从能量密度的角度分析[28]，使用了超表面的聚焦效率η。它可以表示为：

(3)

式中:PF为聚焦范围内的功率强度，Pi为入射功率强度；l为功率强度的半全高宽，如图3(c)所示；pf为y方向上的聚焦范围l对应的功率强度，pi为y方向上，超表面的总宽度y对应的功率强度。

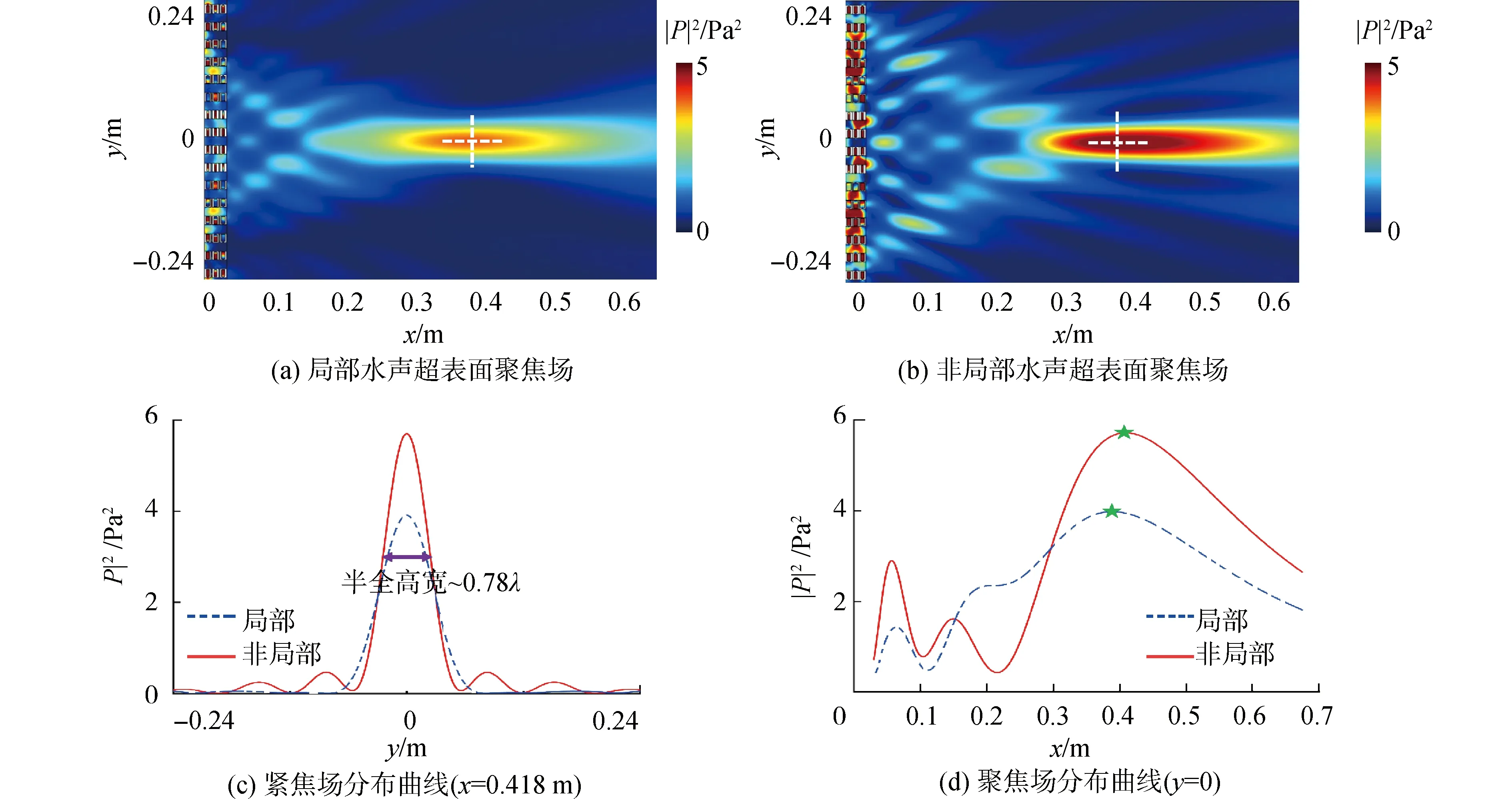
图3 正入射对比Fig.3 Comparison of normal incidence

根据式(3)可以计算出，非局部水声超表面的聚焦效率为48.73%；而传统的局部水声超表面的聚焦效率仅为35.70%。相比之下，非局部设计的聚焦效率比局部设计提高了36.50%。计算结果与仿真预测的结论有着较好的吻合，从数值角度证明了非局部水声超表面的高效性与可行性。为了比较二者对频率波动的适应性，对正入射声压场进行了扫频处理，扫频范围为22.1～24.3 kHz。以首末频率为例，非局部水声超表面的聚焦效率明显更高。如图4(a)、(b)所示，当f=22.1 kHz时，局部设计和非局部设计的峰值分别为2.35 Pa2和4.73 Pa2；如图4(c)、(d)所示，当f=22.1 kHz时，二者的峰值分别为3.63 Pa2和5.46 Pa2。不难看出，同等条件下非局部设计对水声的聚焦操控效果受频率波动影响较小，适应能力更强，具有更好的鲁棒性。

图4 针对频率波动的鲁棒性比较Fig.4 Comparison of robustness against frequency fluctuations

此外，在[-40°～ 40°]的范围内任意调整入射角度，进而对比2种设计的聚焦性能随声压场入射角度变化的波动情况。可以观察到在角度调节过程中，非局部水声超表面的聚焦效果始终优于局部水声超表面。以极限入射角度为例，当入射角度θi=-40°(或θi=40°)时，聚焦声压场功率强度的模拟结果如图5(a)、(b)所示。可以明显观察到，当入射角发生变化时，局部设计的聚焦效果发生了很大程度的削减；而非局部设计对声波聚焦的操控能力几乎不受影响。

图5 斜入射与短焦距聚焦场Fig.5 The focusing fields under the incident acoustic at 40°and with short focal length

为了对比局部设计和非局部设计在短距离处的聚焦效果，将y=0处的焦距fx定义为波长的3倍(即fx=3λ0)，同样地，φ(y)可根据式(2)计算得出。再参考图2(b)、(c)中的2条相移曲线，分别构建局部和非局部水声超表面，变量参数l如表4所示。

表4 短焦距的参数变化Table4 Variable parameters of short focal length mm

在正入射(θi=0°)背景声压场(P0=1 Pa)的作用下，聚焦声压场的模拟结果如图5(c)、(d)所示。图中虚线的交点位置为聚焦点。不难看出，非局部水声超表面在短距离处的聚焦效率仍然明显优于传统的超表面。

4 结论

1)同等条件下，本文提出的非局部水声超表面将聚焦效率优化提高了36.50%；非局部水声超表面在频率波动、入射场角度和焦距变化时仍可保持稳定地高效聚焦。

2)但非局域设计具有“牵一发而动全身”的效果，在引入非局域特征的过程中，可能会产生一些副作用，如：串扰等。

3)本文将非局域思想从量子领域迁移应用至水下声学超材料中，值得注意的是，考虑了水下环境强烈的流固耦合作用。

4)这种非局部设计具有均匀的单元尺寸，在实际的制造和应用中容易实现。有望进一步促进高效超表面在水下信号通信和高分辨率超声成像方面的实际应用。

对于非局域特征引入过程中的一系列附带的作用的产生机制、特点和规律仍需进一步探究。