算法交易提高了我国股票市场的定价效率吗？*

王 凡

（山东大学商学院，山东 威海 264209）

一、引言

随着计算机的普及，全球证券市场的交易方式发生了根本性变化，各国证券市场的大部分交易都实现电子化。利用计算机和算法执行交易决策的方式被称为算法交易。算法交易已经成为股票交易的主流模式，在欧美地区，大部分交易都是通过算法程序完成的。公开数据显示，2018年算法交易占美国股票交易的60%-73%①资料来源：Global Algorithmic Trading Market to Surpass US$ 21,685.53 Million by 2026[EB/OL]. Businesswire, 2019-02-15.，全球算法交易市场规模预计将从2019年的111亿美元增长到2024年的188亿美元②资料来源：Algorithmic Trading: HPC & AI Reference [EB/OL]. Delltechnologies, 2021-10-27.。算法活动在便利交易的同时，也容易造成证券市场出现较大震荡。2010年美国股票市场“闪电崩盘”事件发生，学术界与监管机构等对算法交易的看法开始产生分歧。一方面，算法可以自行制定合理的订单提交策略，确定每一时期提交订单数量、金额与方向，最大限度减少大型订单对市场的冲击，减少交易执行成本。例如，算法交易可以通过跟踪成交量加权平均价格（VMAP）等指标，减少执行成本，在市场动荡时期等待最佳交易时机的到来，有效抑制价格波动。但是另一方面，算法交易的自动快速执行可能会助长暴涨暴跌，不利于证券市场的平稳健康发展。2013年“光大乌龙指”事件的爆发，引起市场对交易结构问题与监管制度漏洞的警惕。2015年，上海公安机关侦破一起涉嫌操纵期货市场的案件，伊世顿公司利用算法交易，2年内非法获利20亿元。

相较于西方国家，我国证券交易市场建立时间晚，依靠人工撮合进行证券交易的历史短，借助技术发展优势与海外经验，电子化交易系统自证券市场建立初期就已然配备。随后，算法交易技术引进国内，融资融券制度和股指期货的推出为算法交易投资提供了更多样化选择，促使这一技术趋势进一步加强，在最大化收益与降低风险的利益驱动下，算法交易被广泛使用。有报告显示，中国的量化基金规模不断增加，2020年备案量化/对冲策略的基金占当年私募证券投资基金数量的30.96%，算法交易在股市总交易量中的占比约为20%-30%③资料来源：中国证券投资基金业年报2020[R].中国证券投资基金业协会, 2020。。

近年来，交易系统的完善和风险防范机制的健全使证券市场恶性事件发生频率变低，且因大多数算法交易对市场的影响不易被察觉、媒体报道减少和技术新鲜感褪去，这一问题不再被投资者广泛关注。当前我国对算法交易的学术研究存在不足，算法交易和程序化交易的定义范围不明确，缺乏合适的度量技术工具，阻碍算法交易本身及对其与当前我国金融市场发展之间关系的分析和理解。鉴于我国证券市场基本制度尚处于不断完善建设中，机构投资者与个体投资者的知识水平距离西方国家仍存差距，股市定价机制运转不够完全顺畅，算法交易所具有的变革性力量如何影响我国股票市场的效率有待进一步考察。诚然，算法交易与人工交易相比有很多优势，算法交易的逻辑准确性和决策执行速度，都能有效降低人类非理性行为所造成的股价波动，提高定价准确度。但是，算法交易也容易利用速度优势，不以成交为目的频繁申报撤单，破坏证券市场秩序，给市场交易效率带来新的挑战。因此，厘清算法交易与我国股票市场关系，在技术变革的同时防范风险，对我国股票市场的健康发展至关重要。算法交易究竟是克服人类弱点的“理性交易者”或“价值发现者”，还是利用人类弱点扰动市场的“投机者”或“趋势跟踪者”？本文将算法交易的定价效率问题引入我国股票市场研究视野，利用实证数据探究算法交易如何影响股票定价效率。

本文可能的贡献主要体现在以下几个方面：第一，本文根据我国交易制度和算法交易执行特点，构建了小单成交量占比和挂单成交占比等代理变量捕捉算法交易活动，为学者与监管层等识别市场中的算法交易提供借鉴。第二，在国外算法交易的影响分析中，学者们往往局限于单一指标分析，不能有效衡量交易方式改变所产生的内在传导机制。事实上，定价效率的改变往往受到证券市场中其他渠道影响。本文结合我国实际背景，通过将股市的波动性、投资者异质信念等纳入到算法交易的影响机制分析中，更全面地对算法交易影响机制进行实证检验。第三，算法交易往往同时在多个交易场所进行，每个交易所都有不同的市场准入条件和微观结构，仅对单一交易所分析存有局限性。本文利用深圳证券交易所和上海证券交易所的数据，能够较为有效地衡量算法交易对我国股票市场的影响。

二、文献综述

（一）算法交易的识别

由于识别算法交易比较困难，大多数研究者利用算法交易的特点寻找算法交易的代理变量。早期学者利用出售算法产品的经纪人数据作为算法交易的代理变量（Hendershott等，2013），但是这种衡量方法并没有从算法交易的本质特点出发且数据频次和样本量均不充足。Bertsimas等（1998）证明了在存在临时价格影响和交易完成期限的情况下，最佳动态执行策略是将订单进行切分。技术进步将这一模型由理论变为现实，陈梦根（2013）认为，算法交易对资本市场的影响主要体现在算法交易通过大单分割减少了对市场产生的冲击，可以有效降低交易成本。夏中宝（2017）也认为，算法交易的起源是为了有效降低大单交易的市场冲击成本，对交易量较大的母单按照特定的交易策略和逻辑由计算机程序进行自动拆分，对拆分后较小子单进行定时定量自动报单交易，从而使整个交易获得更优的成交价格。

在实证研究方面，Hendershott等（2011）利用纽约证券交易所的电子信息流量捕捉算法交易，这些信息流量包括了电子订单提交量、撤单和交易记录等，用每100美元交易量所包含的电子信息量来衡量算法交易，此衡量标准与算法交易拆分大额订单的逻辑相一致。Boehmer等（2021）使用Hendershott等（2011）的方法研究了2001-2011年算法交易对全球42个股票市场的影响。“母单拆分”的特点使得研究者能够从多个维度来衡量算法交易。Weller（2018）利用美国证监会的“市场信息数据分析系统”MIDAS构建了碎股交易量占比、撤单率、订单成交比率、每单交易量四个指标作为算法交易的代理变量，前两个变量与算法交易活动正向相关，后两个则反向相关。因部分证券交易所实现了从源头上对交易主体进行识别，Hendershott等（2013）根据德国证券交易所的自动交易程序（ATP）信息来识别算法交易，这是最早试图直接识别算法交易的研究之一。此后，Dubey等（2021）利用印度证券市场对算法交易订单的独特标识，提高了算法交易识别准确度。在日本证券市场，Saito等（2018）利用高频数据中发出订单服务器的ID来定位使用算法交易的投资者，结合该ID的订单数据来捕捉算法交易动态活动。

（二）股票市场定价效率

在股票价格反映信息方面，基于方差比检验随机游走假设的方法曾经被广泛使用（Lo等，1988；Poterba等，1988；Charles等，2009）。Granger等（1963）在研究股票量价关系时首次提出了“股票价格自相关系数”，随后许多学者利用股价自相关系数衡量当前股价与历史股价的关系（Chan，1993；Chen等，2002；吴崇林等，2021）。可决系数比率被用来衡量个股回报率被市场整体回报率所解释的程度。Durnev等（2003）在Collins等（1994）和Roll（1988）的基础上，将可决系数的差值作为信息量的衡量标准，来反映当前股票价格预测未来收益的程度。Easley等（1987）指出，交易规模会借助改变人们对相关资产价值的看法进而影响证券价格，这也为我们对算法交易影响股票定价提供了理论前提。但Collin-Dufresne等（2015）证明了在衡量此影响时，反映知情交易的措施并不能完全代表知情交易行为。当前测度算法交易影响股票定价效率的过程中，算法交易者如果仅是依据价格与成交量等公开信息进行交易，尽管能促进价格对信息的获取，但此类交易并非完全是知情交易，上述模型所衡量的真实信息量也可能是较低的。Morse（1981）和Meulbroek（1992）探究了股价在信息公告前后的反映机制，其使用价格跳跃比率来衡量盈利公告前的价格变化。Meulbroek（1992）在论证内幕交易是否影响股票价格时，使用累计异常收益来判断内幕交易收益是否显著，这些衡量标准都较为有效地避开了信息纳入价格方式的干扰。Weller（2018）则认为，累计异常收益虽然衡量了在公司公告之前提前纳入价格的信息量，但缺乏对未纳入价格信息水平的衡量；其将累计异常收益进行标准化，以公告后价格变动与公告前包含公告的价格变动比率衡量信息纳入。

现有涉及资产定价效率的文献主要集中在以下领域：在政策方面，学者们研究了融资融券（许红伟和陈欣，2012）、卖空机制（李志生等，2015）、发行机制（周孝华等，2006）、资本市场双向开放（彭红枫和万洋，2022）等对定价效率的影响；此外，还有相关研究者衡量新闻媒体报道（黄俊和郭照蕊，2014； 熊艳等，2014）、机构投资者（李志辉等，2021）、知情交易（陈国进等，2019）以及投资者情绪（Luo等，2021）等因素对股票定价的作用机制。上述学者在当时的背景下有效评判了市场新兴现象对证券定价效率的影响。然而遗憾的是，算法交易作为当前较为常见的交易方式，鲜有研究者从算法交易的视角分析其对我国股票市场定价效率的影响。

（三）算法交易与股票市场定价效率

以往文献表明，算法交易对证券市场能产生很大影响。Brogaard等（2014）探究了高频交易商在价格发现和价格效率方面的作用，发现无论是在市场波动平缓时期还是在波动剧烈时期，高频交易商都能在永久性价格变化方向或过渡性定价错误的相反方向进行交易，从而提高价格效率。此外，算法交易的预测与信息纳入并非将其信息公开化，算法交易本身很可能只是一种趋势捕捉和行为识别模仿。Grossman等（1980）认为信息是存在成本的，算法交易前期建设成本高，但投入使用后边际成本较低，较低的交易成本会鼓励信息的收集和纳入。Hendershott等（2011）认为收回建设成本的需求导致交易商在回报率较高的证券中投入算法交易，这也解释了为何算法交易显著减少了较大市值股票的价差和逆向选择程度。Foucault等（2016）对知情投机者在消息公布前进行交易（“快”）和公布后交易（“慢”）的最佳交易策略进行比较后发现，虽然投机者交易与消息公布前后的短期价格变动密切相关，但投机者也会根据其对资产长期价值的估计进行交易，从而为价格发现做出贡献。Weller（2018）从动态角度衡量信息价格效率，将价格信息含量作为评估要素，利用美国证券市场的季度面板市场数据研究后发现，尽管算法交易对于信息转化进价格非常重要，但同时也可能阻碍信息获取并降低可获得信息的价格效率。刘鹏（2019）指出，程序化交易促使资本市场联动、协同定价现象的产生，在社交平台、信息技术公司的影响下，程序化交易的耦合效应使得资本市场波动性加剧、风险传染性更强。Boehmer等（2021）从全球股票市场角度探究算法交易对市场质量的影响时，将流动性和波动性纳入衡量的视角，结合信息效率综合评判对整个市场的影响，发现算法交易会产生较窄的有效价差，提高市场流动性；同时，日内回报的自相关绝对值也相对较小，提高了信息性。Chakrabarty等（2022）探究了算法交易在新冠疫情期间对美国股市流动性的作用，发现算法交易并没有降低市场流动性，也没有降低股市定价效率。从以上文献可以看出，虽然衡量算法交易对市场影响并不存在技术复杂性，但其中的影响机制较为多元，其中特定市场结构与特性传导渠道的探究成为研究的重点趋势。

三、理论分析与研究假设

以往文献基于算法交易效应分析，大多认为算法交易能够加快股票对信息的纳入，交易方向与错误定价方向相反，对股票定价效率具有正向促进作用，但是多数文献缺乏对我国市场定价效率特定影响的探讨。尤其是由于我国“T+1”交易制度对高频交易的限制，A股市场尚无做市商制度和指令驱动交易制度，散户投资者比例较大，市场羊群效应较为显著，算法交易的技术优势与理性特点可能会发挥更强的效力。具体来看，算法交易能够分割大单委托指令，运用算法构建组合选择并制定交易策略（Nuti等，2011）；超越人类对信息价格的反应速度，更快地将市场信息纳入价格，增强市场短周期内的价格反映，有力提高盈利公告时的定价效率（Chakrabarty等，2015），降低市场整体买卖差价（Jovanovic等，2016）。此外，算法交易还能在股指期货方面发挥定价纠正作用，加强期货市场与股票市场之间的联系，减少市场延迟，提高股票市场定价效率（Zhang，2018）。基于此，本文提出以下研究假设：

H1:算法交易能显著提高我国股票市场定价效率。

算法交易可以跟踪成交量加权平均价格（VWAP）指标，以减少执行成本。这一点表明算法交易在市场价格动荡时期可能会等待最佳价格才得以执行（Hendershott等，2011）。Hendershott等（2013）、Jarnecic等（2014）研究表明，算法交易能在市场剧烈波动时提供持续流动性，增加市场价格弹性，有效抑制价格波动，算法交易的撤单行为也并未在高波动时期变得更加频繁（Groth，2011）。从算法交易执行速度上来看，Gsell（2008）发现算法交易的低延迟会降低市场波动。以算法交易为代表的技术进步可以有效地减少摩擦对交易和资产价格动态变动的影响（Duffie，2010），有效缩短搜索时间，同时通过将大订单分成小订单来减少市场影响（Bertsimas等，1998），稳定市场波动性。Groth（2011）从算法交易策略同质化角度反证，算法策略和人类策略同样多样化，算法交易者作为一个整体不存在羊群效应，也不会据此增加波动性。目前针对高频交易与公告前后价格变化的研究（Boehmer等，2021；Scholtus等，2014）大多都注重评判以秒为单位的波动性。由于我国并无短期持仓并频繁交易的市场条件，这方面的影响力较弱，且这也并非是我国投资者们关注的重点，因此本文的分析更倾向于中长期影响。基于此，本文提出以下研究假设：

H2：算法交易能够降低我国股票市场波动性，进而提高股票市场定价效率。

算法交易通过计算机系统执行交易，可以很大程度上避免人类交易所产生的非理性行为。行为金融学认为，过度自信等心理偏差会带来高估或低估股价等问题。信息经济学认为对于均衡价格的信念不同是交易发生原因之一，在资产定价过程中的人类投资者即使拥有相同信息，也会形成对股票价格的不同预期，即异质信念（Grossman等，1980）。Miller（1977）证明了在卖空约束机制下，投资者异质信念是影响资产价格的重要因素，异质信念越强烈，股票价格偏离均衡水平的程度也相应越高，随后这一理论被大量学者所证明（Harrison等，1978；Smith等，1988；张维和张永杰，2006）。我国股票市场建立时间较晚，散户投资者占比较高，心理偏差所带动的投机氛围较为强烈。我国虽然在2010年出台了融资融券制度，但机制设计上仍然不利于卖空，异质信念的股价效应仍然具有理论与现实意义（包锋和徐建国，2015）。相对理性的交易方式能够对股价均衡产生影响。算法交易虽在某种程度上可以看作是人类意识的延伸，但是其在具体执行方面并不具备人类思维，可以看作是较为理性的投资者。因此，算法交易的发展在我国可能对投资者异质信念产生更大程度的影响，进而影响股票价格均衡。基于此，本文提出以下研究假设：

H2b：算法交易能够减缓我国股票市场异质信念程度，从而增强股票市场定价效率。

四、研究设计

（一）数据来源与样本选取

本文数据来自于CSMAR国泰安数据库与RESSET锐思数据库中上海证券交易所与深圳证券交易所A股市场2016—2021年的股票日度数据。对所搜集的数据进行了相应处理：去掉样本区间内被特殊处理和首次上市的股票，剔除金融行业类股票，删除关键变量缺失的样本，同时对所有的变量进行了上下1%水平的Winsorize缩尾处理以避免极端值影响。最终得到了1923支股票共计415.54万个日度观测样本数据。

（二）变量定义

1.核心解释变量：算法交易

我国交易所尚未实现对算法交易产生订单的单独标识，因而无法直接观察到某一单是否由计算机算法产生，需依靠相关代理变量。鉴于我国目前算法交易尚不具备高频条件，交易频率和交易自动化程度与成熟证券市场尚有一定区别。在变量选取时，单纯借鉴电子信息流量比率（Hendershott等，2011）和撤单率（Weller，2018）等指标有失偏颇。基于制度框架和投资者水平限制，我国目前的算法交易大多为基础算法交易类型，例如成交量加权平均价（VWAP）、时间加权平均价格（TWAP）、时间比率成交（TPOV）等，此类算法的主要特征为对较大母单进行拆分，择时择量地按照不同的基准价格策略对子单进行交易。现有文献表明，较高的小单交易比率表明有更多的算法交易，交易中小型订单所占比例是与算法交易的强度成正比的。

本文基于Weller（2018）与Hendershott等（2011）对算法交易识别的方法，并结合我国算法交易本身的特征，将我国股票市场连续竞价阶段的小单成交量占比STR作为算法交易代理变量。鉴于我国个人投资者数量众多的独特市场微观结构，小单成交量占比STR对算法交易的识别可能存在噪音干扰，本文又构建了挂单成交占比OTR来更全面准确衡量算法交易活动。

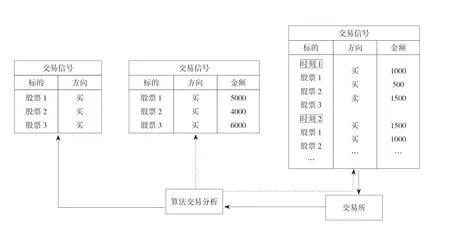
图1 算法交易示意

算法交易的第一个代理变量是小单成交量占比STR，表征小单成交量占总成交量的比例，其计算公式如下：

算法交易的第二个代理变量是挂单成交占比OTR，测度股票交易中申报价格次数与需撮合成交笔数之间的比例，其计算公式如下：

2.被解释变量：定价效率

Hou等（2005）提出利用股票价格对信息的延迟来描述影响股票市场摩擦的严重程度，此种方法被不少学者（Saffi等，2011； Blau等，2017）所采用。李志生等（2015）基于上述方法，将我国证券市场的股票日度收益率以及滞后市场收益率进行回归，构建股价信息反应滞后指标来衡量我国股票市场的定价效率。方立兵和肖斌卿（2015）则将信息反应滞后指标进行修正，以保持与定价效率的正向一致性。本文参照了上述研究，将滞后的市场收益率对个股的解释程度作为定价效率的代理变量，构建了Efficiency1和Efficiency2两个指标。具体的测算方法如下：

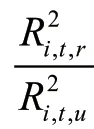
为了将上述构建方法与定价效率的正向性保持一致，本文参考方立兵和肖斌卿（2015）做法，将上述指标进行修正，把个股i的第一个定价效率指标定义为：

从式（6）可以看出，定价效率指标Efficiency1i,t与信息反应滞后指标Delay1i,t的主要区别在于，前者是后者的倒数，这能确保两者之间的经济意义保持一致，并且指标Efficiency1i,t越大，则该支股票的定价效率越高。

除了利用回归方程的可决系数，还可利用回归方程中解释变量的参数值来衡量即期股票收益率被历史市场收益率可解释的程度，其信息滞后反应指标可表示为：

Delay2i,t可理解为滞后市场收益率的回归系数占包含即期回归系数的比重，其取值越大，则定价效率越低。为了保持与定价效率的正向一致性，将上述指标取倒数，第二个定价效率指标定义为：

由上式可知，指标Efficiency2i,t越大，表明股票的定价效率越高。

3.其他变量

本文的中介变量为波动性与异质信念。对于波动性的衡量，采用较为直观的股票20日简单移动平均收益率的波动率（Voli,t）来衡量。对于异质信念，参考以往文献做法（Hong等，2007；Boehmer等，2006； 张峥和刘力，2006），采用换手率（Turnoveri,t）作为投资者异质信念波动代理变量。

为了控制影响定价效率的其他因素，参考Hendershott等（2011）、李志生等（2015）、侯宇和叶冬艳（2008）的研究，在模型中引入有效价差（Rspread）、知情交易概率（Vpin）、收盘价（Clpr）、流通市值自然对数（Trdshr）、日收益率（Dret）以及20日简单移动平均市场收益率标准差（Stdmr）作为控制变量。文中所有变量定义见表1。

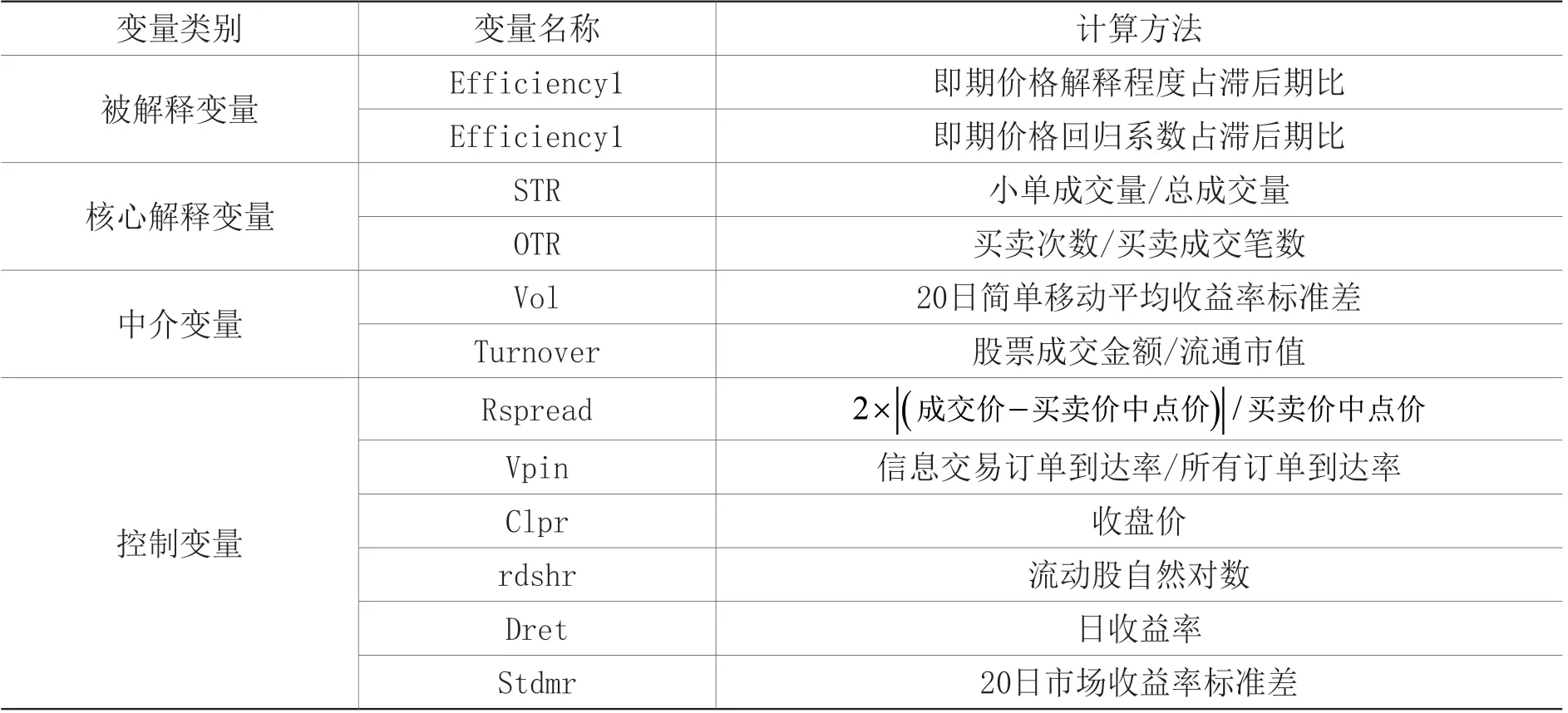
表1 变量定义

（三）模型设定

为了检验假设1，本文建立如模型（9）所示面板数据回归模型，其中ATi,t为捕捉算法交易活动的STR指标与OTR指标，Controlsi,t为控制变量，θi,t和λi,t分别为行业固定效应和时间固定效应。若β1显著为正，则表明算法交易提高了我国股票市场的定价效率。

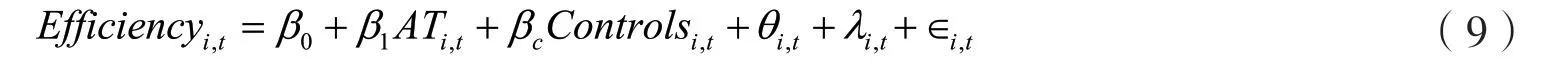
为了检验假设2a，本文建立如模型（10）-（12）所示的面板数据回归模型。若回归系数β1显著为负，且模型（12）中β2显著为正，则说明算法交易确实能通过减轻股票市场波动性，提高股票定价效率。

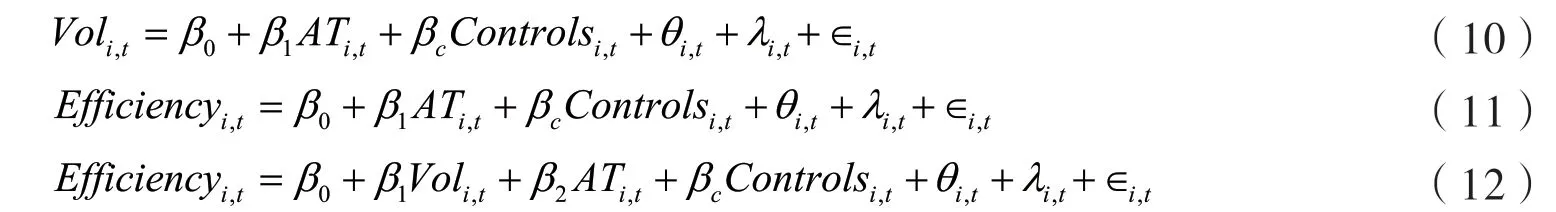
为了检验假设2b，本文建立如模型（13）-（15）所示的面板数据回归模型。若回归系数β1显著为负，且模型（15）中β2显著为正，则说明算法交易确实能通过改善投资者异质信念情况，提高股票定价效率。

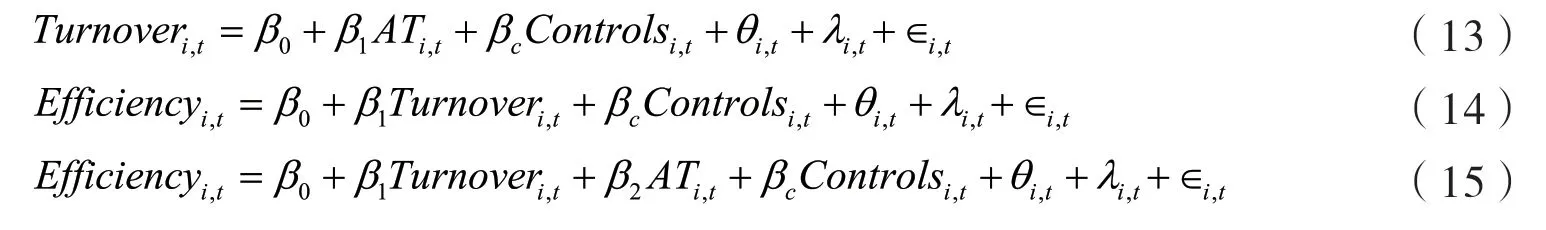
五、实证分析

（一）描述性统计

从表2的描述性统计中可以看出，我国股票市场小单成交量占比均值约为0.274，买卖次数占买卖成交笔数的均值约为0.335，即平均一次买卖大概需3笔交易才能完成。股票市场的日均换手率为2.6%，远高于发达资本市场，说明投资者对未来股票价格的预期存在较大的不一致性。

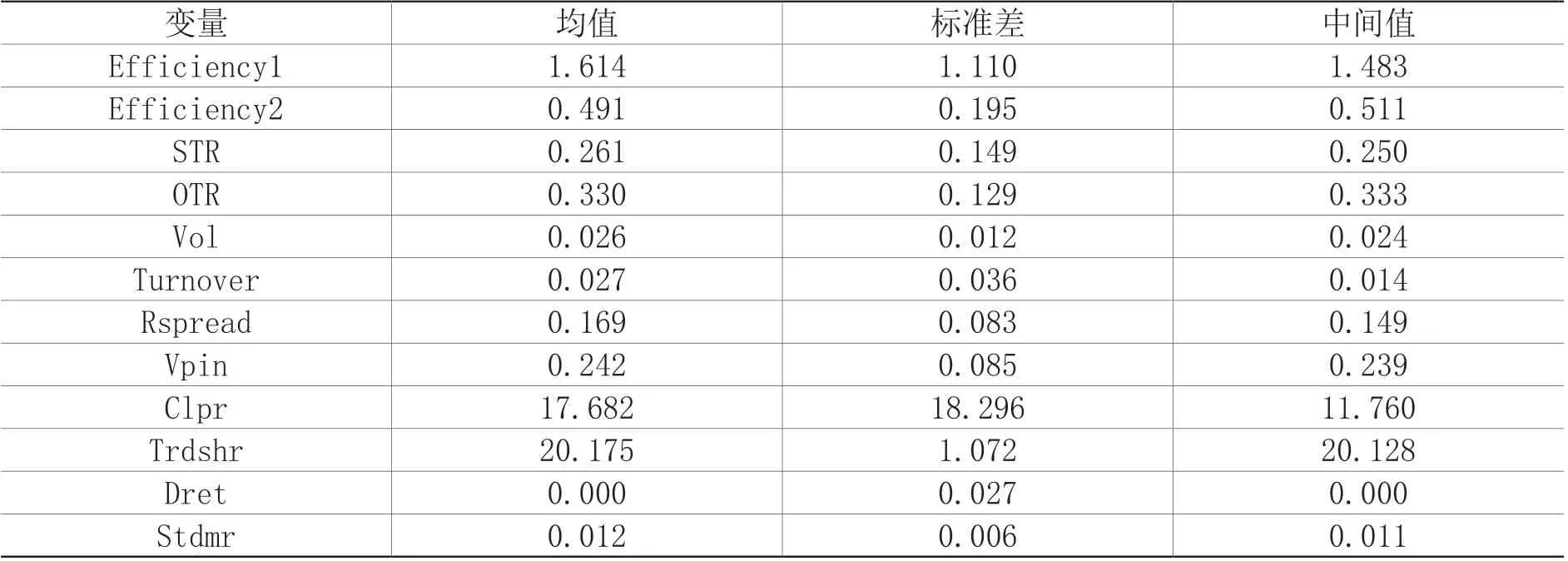
表2 描述性统计

（二）回归结果分析

1.算法交易对定价效率的基准回归结果分析

本文基于模型（9）对算法交易与股票定价效率之间的关系进行检验，回归结果如表3所示。在控制了其他可能影响定价效率的影响因素之后，算法交易STR与OTR与市场定价效率Efficiency1及Efficiency2在1%显著性水平下显著为正。这说明算法交易的运作能够显著提高股票市场定价效率，这与前文的分析与假设结果相一致，即假设1成立。进一步采用Hausman检验测度在固定效应和随机效应模型下回归结果的有效性，结果显示固定效应优于随机效应，因此本文参照基准为固定效应模型。

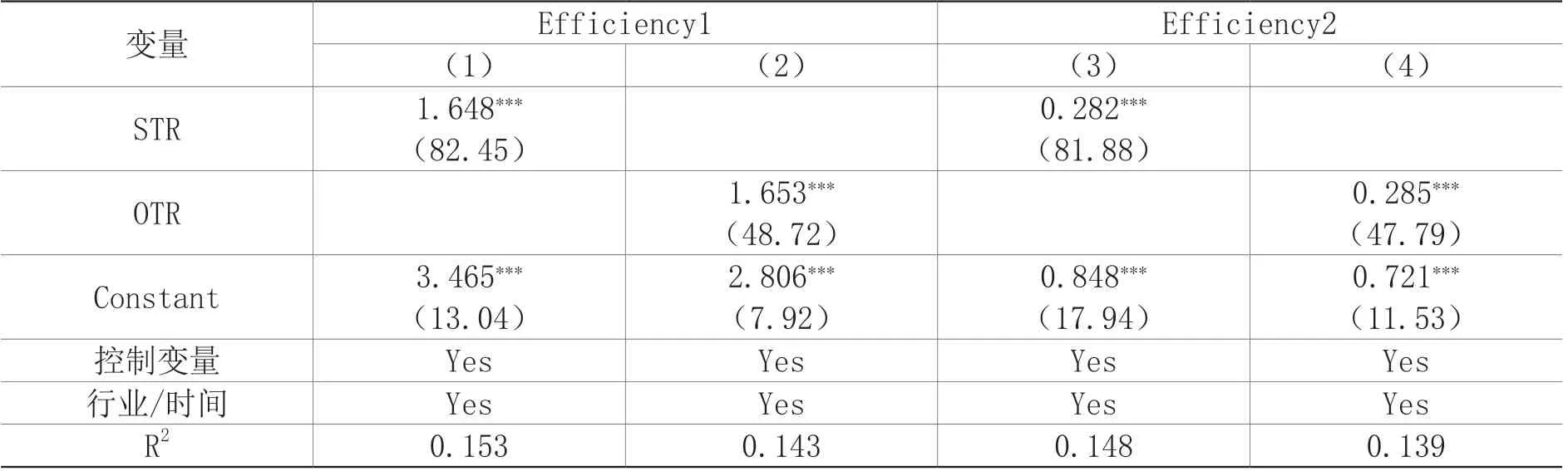
表3 算法交易对定价效率的影响

2.基于减轻波动和减缓异质信念的中介机制检验

表4报告了算法交易对定价效率中介机制的回归结果，其中Panel A为减轻波动的中介效应检验，Panel B为减缓异质信念的中介效应检验。从列（1）（2）的结果可以看出，STR与OTR对Vol的回归系数均在1%显著性水平下显著为负，说明算法交易确实能够减轻股票市场波动；从列（3）-（6）的回归结果来看，STR与OTR回归结果在1%显著性水平下显著为正，而Vol的回归系数显著为负，表明算法交易通过减轻股票市场波动性提高了股票市场的定价效率，假设2a成立。

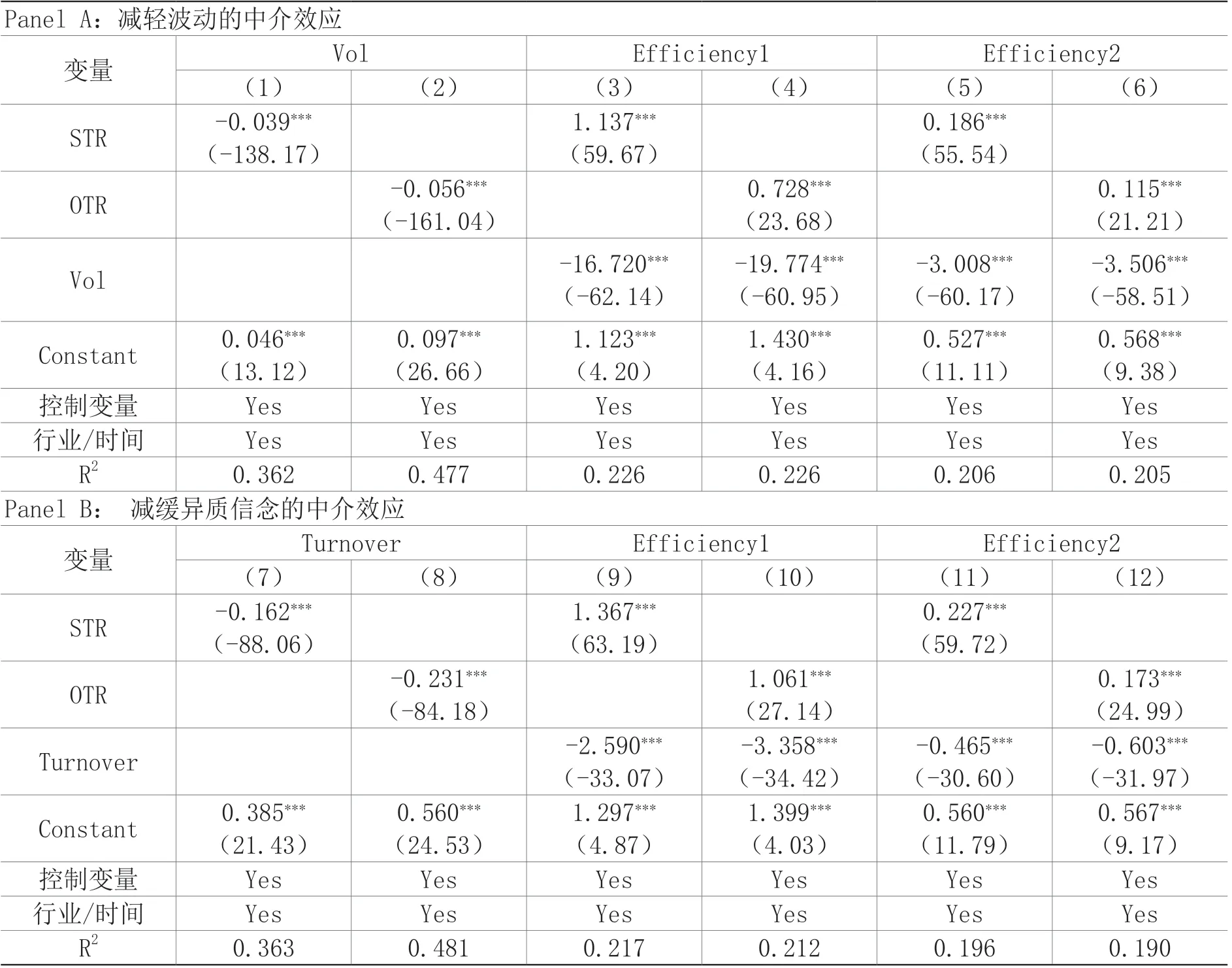
表4 算法交易影响定价效率的中介机制检验

从列（7）（8）的结果可以看出，STR与OTR对Turnover的回归系数均在1%显著性水平下显著为负，说明算法交易可以有效减缓投资者异质信念波动，改善市场投机性意愿；从列（9）-（12）的结果可以看出，STR与OTR在对定价效率的回归中加入Turnover后系数在1%显著性水平下显著为正，而Turnover的回归系数显著为负，表明算法交易可以通过减缓异质信念有效提高股票市场定价效率，假设2b成立。

（三）稳健性检验

1.替换算法交易代理变量

“母单拆分”是当前我国算法交易的主要策略，并针对这一策略产生了多维度的衡量标准。考虑到算法交易难以捕捉，算法交易的衡量准确性可能会对定价效率回归结果产生影响。为了降低“实证结果依赖于算法交易代理变量构建”的担忧，本文继续利用算法交易特点，选取小单申报占比SOR作为定价效率指标进行稳健性检验，验证前文算法交易代理变量选取的合理性。变量的具体定义如下：

替换算法交易测度指标后的回归结果如表5列（1）（2）。可以看出，SOR的回归系数在1%显著性水平下显著为正，这表明算法交易对股票市场定价效率具有提升作用的假设依然成立。

2.工具变量回归

为了进一步减少对算法交易的测量误差或遗漏变量问题产生的内生性问题，本文参考Boehmer等（2021）的方法，将触发沪深交易所股价异动信息披露标准的营业部地理位置作为工具变量。当披露的营业部处于深圳或上海时，工具变量Dumlocation赋值为1，未披露或处于其他地理位置时，Dumlocation赋值为0。该工具变量符合相关性与外生性的约束条件：一方面，触发沪深交易所股价异动信息披露标准的营业部具有使用算法交易的动机和实力，同时交易服务器位于交易所所在城市能减少订单提交延迟，降低延迟成本；另一方面，将营业部服务器靠近交易所附近，交易延迟的降低也并不能提高市场流动性，与定价效率并无关系。表5列（3）-（6）的回归结果显示，在考虑算法交易与定价效率之间可能存在的内生性问题之后，加入工具变量的回归系数在1%显著性水平下显著为正，表明算法交易能够显著提高定价效率，与前文的假设和验证相一致。

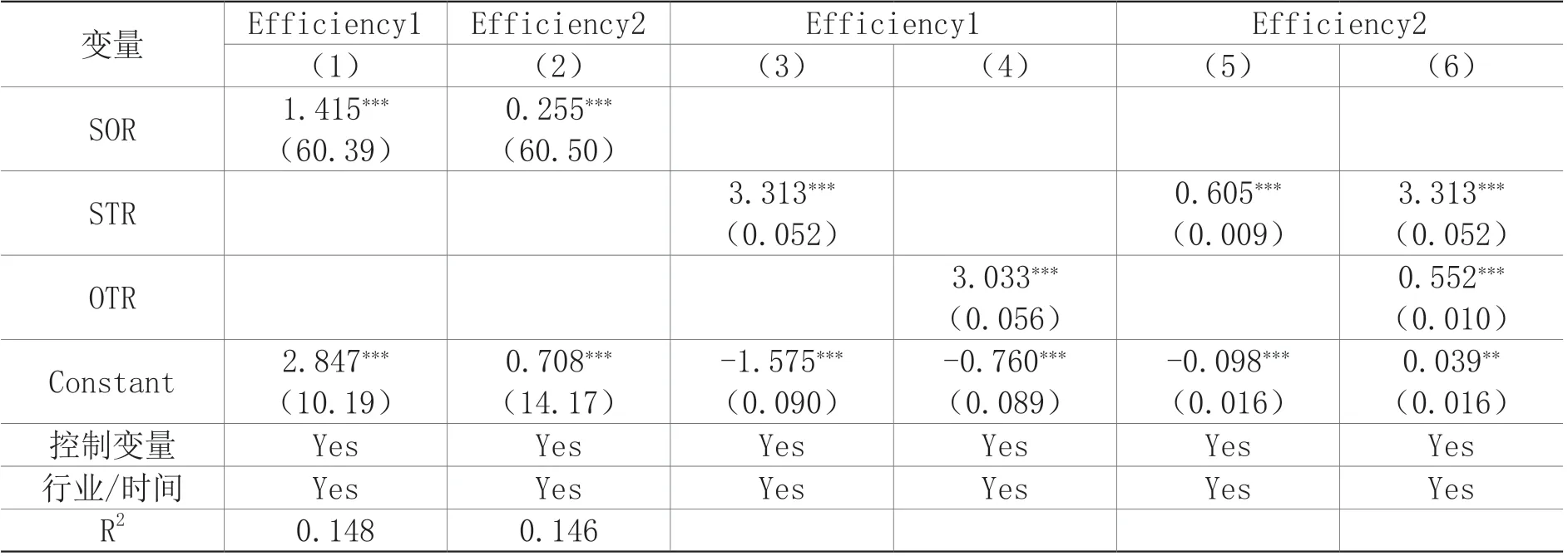
表5 稳健性检验结果

六、异质性分析

（一）股票价格的异质性影响

前文研究表明，算法交易提高了股票市场定价效率，但基于我国股票市场的最小报价单位制度，股价的高低对算法交易的活跃程度可能也会产生影响。A股的最小报价单位为0.01元，假设每股1元的股票与每股5元的股票均变动0.01元，所产生的价格变动幅度是显著不同的，前者价格变动了1%而后者变动了0.2%，这说明最小报价制度为不同股票价格划分了不同价格变动精细程度，高市价股票的价格精细程度更高。同样，在变动幅度相同的情况下（例如1%），高市价股票要比低市价股票变动的绝对价格更多，更需要交易者修改报价；而算法交易的持续更新订单与切分订单能力都使得其在高市价股票上的交易能力更强且交易效率更高。

基于上述分析，本文将股票价格按照低、中、高分为3组，分别对这3组进行算法交易与定价效率的回归，回归结果如表6所示。本文发现，在定价效率与算法交易的不同衡量指标回归中，回归系数随着股价的提升而增大，且均在1%显著性水平下显著为正。这与前文的预想相一致，即算法交易对定价效率的促进作用随着股价的升高而提升。

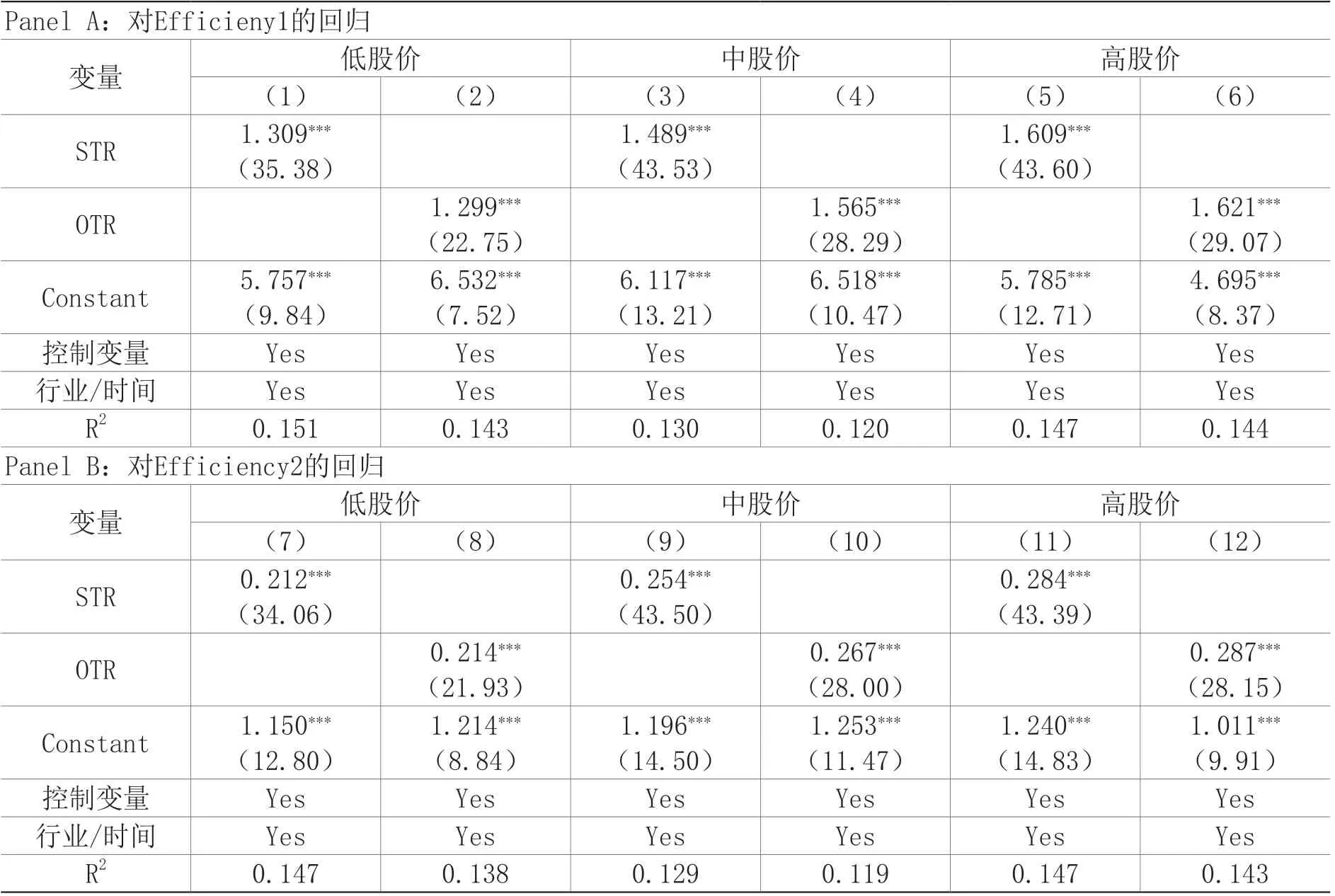
表6 股票价格的异质性影响

（二）市场流动性的异质性影响

为进一步验证算法交易在促进定价效率时是否受到流动性条件的影响，本文采用非流动性指标Illiq来衡量市场流动性，当Illiq低于过去20个交易日的均值时，说明流动性水平较高，虚拟变量Dumliq取值为1，否则取值为0。在模型中引入Dumliq以及算法交易与Dumliq的交乘项，实证结果如表7所示。算法交易变量STR、PTR以及它们与Dumliq的交乘项的回归系数均在1%显著性水平下显著为正，说明算法交易在市场流动性充足时更有助于促进定价效率。

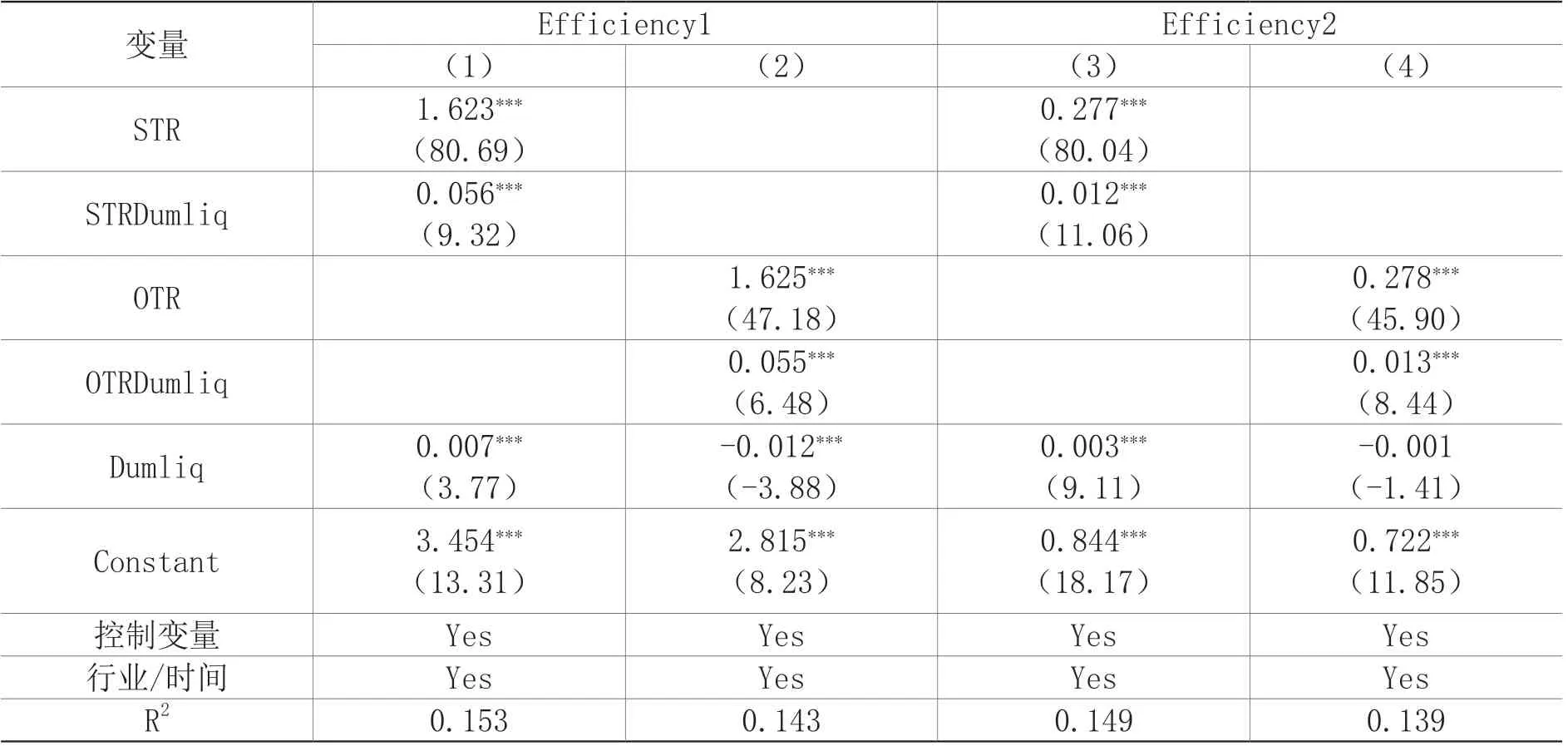
表7 市场流动性的异质性影响

（三）市场情绪的异质性影响

股票市场的定价效率容易受到投资者羊群效应的影响（吴崇林等，2021；许年行等，2013；孙怡龙和凌鸿程，2019），因此本文检验算法交易能否在市场情绪高涨中保持提升定价效率的稳定性，甚至是在市场情绪高涨时发挥更强效力。本文设定CSSD（横截面收益标准差）指数20日滚动均值高于样本当年中位数时，羊群效应出现，虚拟变量Dumcssd取值为1，否则取值为0。在模型中引入Dumcssd变量以及算法交易与Dumcssd的交乘项，回归结果如表8所示。相比于市场情绪平缓（羊群效应未发生），算法交易在羊群效应下对定价效率的促进作用更强。这说明在市场定价受到情绪影响而偏离时，算法交易不仅没有受到羊群效应的干扰，反而能利用市场错误定价发挥更强的价格纠正能力。

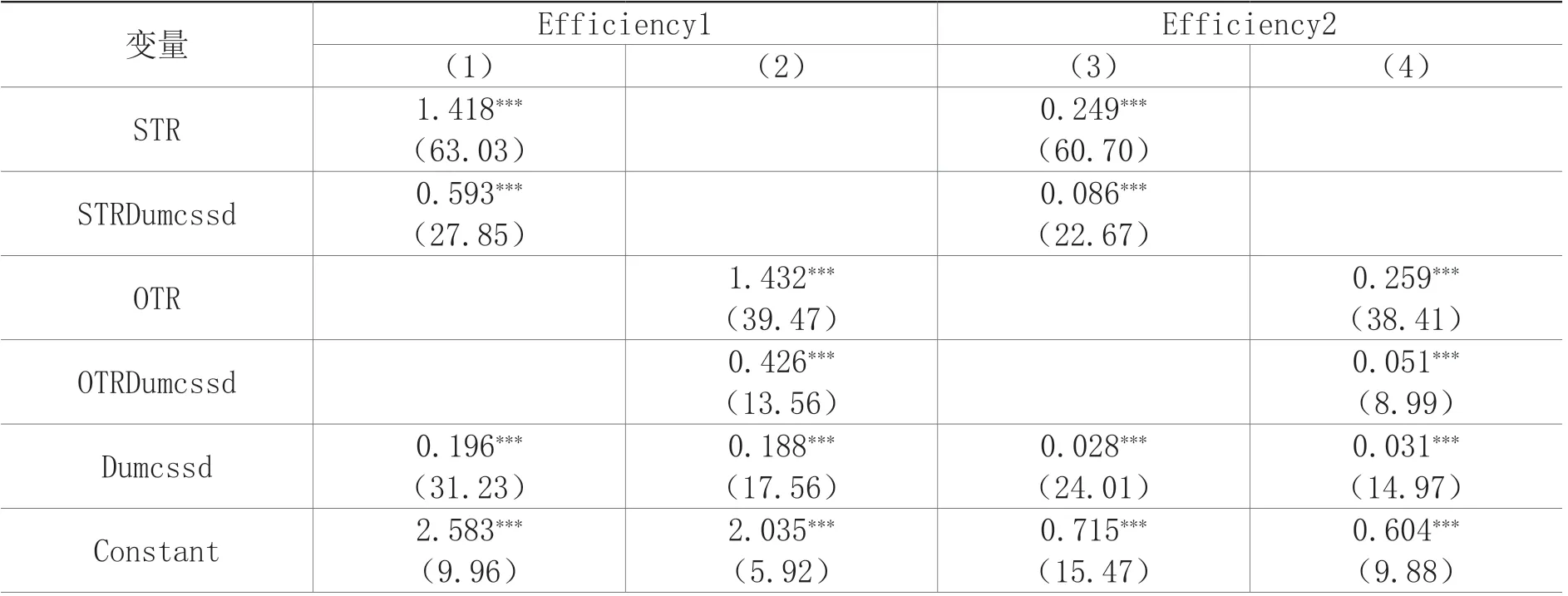
表8 市场情绪的异质性影响

控制变量 Yes行业/时间 Yes R2 0.181 Yes Yes Yes Yes Yes Yes 0.166 0.168 0.155

七、结论与建议

本文以2016—2021年A股股票数据为样本，结合我国现阶段市场交易结构和制度特点，采用小单成交量占比、挂单成交占比、小单申报占比以及每百元成交股数所包含订单量等代理变量来测度我国算法交易活动，实证分析算法交易活动对定价效率的影响。实证结果显示：第一，算法交易能有效提高我国股票市场定价效率，上述结果在控制了内生性等问题后依然显著。第二，中介效应分析发现，算法交易对股票市场波动性的减轻以及对投资者异质信念的减缓是提高定价效率的重要途径。第三，拓展性分析发现，算法交易对不同股票的定价效率存在差异性影响，对高市价股票的定价效率提升程度最高；同时在市场流动性充足的条件下，算法交易能更好地发挥作用；此外算法交易还能有效克服市场羊群效应，改善错误定价。

本文的研究结论能够为提升我国算法交易市场认知、合理引导机构投资者应用算法交易、完善证券市场算法交易监管、有效防控证券市场崩盘风险，在实践和政策层面带来以下启示：

第一，为算法交易提供有利的发展环境。鉴于算法交易在提高股票市场定价效率、减弱市场波动方面具有显著的正面影响，我国应为证券市场信息技术的发展提供更多政策支持，加强证券市场的数字基础设施建设，例如提供主机托管业务来提升订单传播速度等。明晰算法代码及数据本身的法律属性并将其纳入知识产权保护法律框架内进行有效确权，激发市场主体的创新动力，避免“算法趋同”造成的市场股价波动与非理性恐慌。

第二，加强对算法交易的监管。算法交易即使在发达资本市场中仍然具有制造不稳定因素的风险，我国应吸取经验教训，提前谋划算法交易发展，完善算法交易监管体系。其中，可供考虑的举措是对市场交易中的算法交易活动采用单独标识，提高市场透明度，从而有效防范多层嵌套和技术遮盖手段下的监管套利。对算法交易订单进行标识也为监管机构构建算法交易跟踪监管系统提供了底层技术支持，维护金融体系整体稳定和市场良性运转。