浮冰作用下单桩海上风机动力响应分析
2022-10-09张礼贤施伟周昳鸣李昕
张礼贤,施伟,2†,周昳鸣,李昕,2
(1.大连理工大学建设工程学部,辽宁大连 116024;2.大连理工大学海岸和近海工程国家重点实验室,辽宁大连 116024;3.中国华能集团清洁能源技术研究院有限公司,北京 102209)
随着化石能源的不断消耗,发展可再生能源成为促进各个国家能源经济发展、能源转型的重要措施之一.2016 年,国家能源局印发《风电发展“十三五”规划》[1],明确了海上风电的发展目标.海上风机基础型式主要分为固定式和浮式[2-4],我国近海水深较浅,主要以固定式风机为主.辽宁省环渤海地区风场条件较为优异,已陆续规划花园口、庄河等海上风电场.辽宁省大连海区每年冬季都结冰[5-6],属于我国冰情较为严重地区,一般每年冰期约为3 个月.因此,在渤海湾地区,冰荷载对海上风机动力响应的影响应重点考虑.
当前,冰激振动激励研究仍未有定论[7].具有代表性的海冰动力荷载分析理论主要有:强迫振动理论以及自激振动理论.Matlock 等[8]基于强迫振动理论,建立浮冰加载过程中弹簧阻尼数值模型.Kärnä等[9]根据实测数据,提出锯齿形冰力函数来计算海洋结构自激振动响应.Yue等[10]根据渤海海洋平台实测资料,提出不同冰速下的冰激振动模型.近些年来随着固定式海上风机的不断发展,越来越多的研究开始关注冰荷载对固定式海上风机的影响.王国军等[11]基于ANSYS 有限元数值分析方法开展了三桩海上风机在浮冰作用下的动力响应研究.吴泽等[12]设计了安装抗冰锥结构的物理模型实验.黄焱等[13]采用锥形结构动冰力函数的方法开展了三桩式海上风电结构的冰激振动分析.张大勇等[14]开展了渤海地区海上风机的抗冰性能分析.Shi等[15]及Zhou等[16]基于HAWC2 开发海上风机冰荷载数值计算模块.Wang[17]对Kärnä 冰力谱模型以及Määttänen-Blenkarn 模型进行对比分析,分析各自模型优缺点.
本文在上述研究基础上,基于渤海某海域实际冰情,开展NREL 5MW 单桩海上风机不同冰载数值模型下的结构动力响应分析,探究冰速、冰厚等冰参数对结构动力响应的影响规律,并对采用抗冰锥措施的单桩海上风机动力响应进行对比分析.
1 风机荷载计算模型
1.1 空气动力学荷载
本文采用叶素动量理论[18-19]计算作用于风机叶片的空气动力荷载,叶素动量理论将风机叶片沿径向离散成各个独立的叶素单元,并做出如下假设:(a)不考虑叶片的沿径向相邻的叶素单元之间的干扰;(b)作用在每一个叶素单元上的气动力载荷在圆环方向上保持恒定,且每个叶素单元受到的气动载荷仅仅由叶片本身翼型的气动性能所决定;(c)不考虑叶片长度对气动力载荷影响.
1.2 冰载计算理论
1.2.1 Matlock冰载模型
Matlock 模型主要分为单齿模型和双齿模型.采用单齿模型计算时,假定冰齿之间的距离大于冰齿的最大弹性变形,其计算模型如图1如示.
图1中,Z0为第一个冰齿初始计算时所处位置;x为结构位置;M为结构质量;K为结构刚度;C为结构阻尼;Pch为冰齿间距;Δ为冰齿变形;N为冰齿数量.

图1 动冰荷载计算模型Fig.1 Diagram of dynamic ice load model
单齿随机冰荷载的冰力函数F如式(1)所示.

式中:Kice为锯齿刚度;Δmax为冰齿最大变形.
区别于单齿计算模型,双齿计算模型考虑了冰最大变形大于冰齿之间的距离的可能性,其数值计算模型如式(2)所示.

式中:Pch为冰齿间距.
1.2.2 非同步失效冰载模型
在非同步失效计算模型[20]中,考虑随机冰厚与接触宽度之间的关系,假定接触体积为L⋅L⋅L,其中L为冰齿宽度.冰荷载的数学计算模型如式(3)所示.
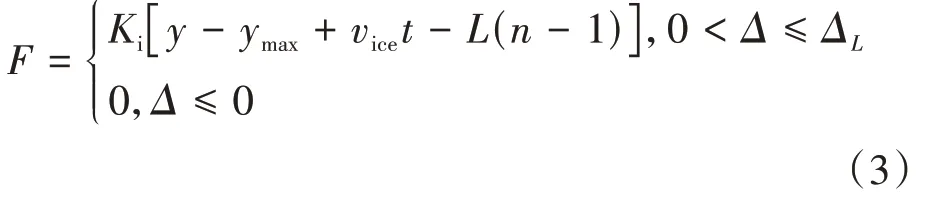
式中:y为失效区域初始接触位置;vice为冰速;t为加载时间;n为冰齿编号;Ki为冰的刚度.
1.2.3 弯曲破坏计算模型
之前所有的数值计算模型,结构均为直立结构,对于带有斜坡的结构,冰的破坏更多的可能是弯曲破坏而不是挤压破坏.由于冰荷载弯曲破坏所产生的力较小,作用在结构上的力也会较小.Ralston 模型[21]考虑圆周和侧裂的影响,弹性地基反应、冰变形和冰泡在圆锥结构上起作用.水平冰力可表示为:
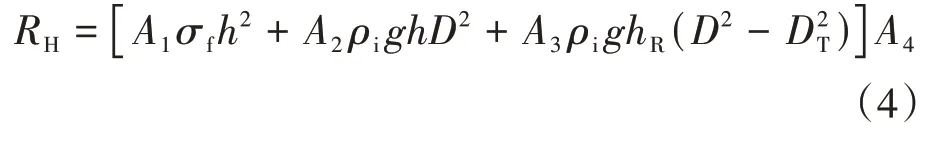
式中:A1、A2、A3、A4为计算系数,具体取值详见文献[21];σf为结构的弯曲强度;h为冰厚;D为结构的直径;ρi为冰的密度;hR为积冰厚度;DT为圆台上部厚度;g为重力加速度.
2 数值计算模型
2.1 风机数值模型
本文选取的风机数值模型为美国可再生能源实验室开发的5 MW 单桩海上风机[22](图2),该风机为三叶片水平轴风力发电机,采用变速变桨控制策略.模型计算水深为20 m,详细参数如表1所示.

图2 NREL 5 MW风机模型示意图Fig.2 Diagram of NREL 5 MW wind turbine

表1 NREL 5MW风机参数Tab.1 Parameters of NREL 5MW wind turbine
2.2 工况定义
基于渤海海域的相关海况,制定冰风联合工况.在一体化风机模型中,风载荷主要作用在叶片上;采用多种冰载计算模型进行冰荷载的计算.采用强迫振动模型时,浮冰的破碎频率为破碎长度除以冰速.为此,本文重点探究风冰联合工况下,冰力频率接近塔筒一阶频率(0.267 Hz)冰况下海上风机的动力响应特性.选取额定风速11.4 m/s 和湍流度0.12,风载荷作用的时间平均为1 000 s,本文重点考虑冰荷载对结构动力响应的影响,冰速与冰厚分布见表2.

表2 浮冰工况Tab.2 Combination of ice-wind load cases
3 结果与讨论
3.1 不同冰载数值计算模型冰荷载对比
图3 为不同冰载数值模型下的单桩海上风机所受冰荷载的时程曲线对比.采用不同冰载数值模型计算时,单桩海上风机所受冰荷载不同.采用Matlock 双齿模型计算时,单桩风机所受冰荷载最大,最大约为3 500 kN;采用非同步失效模型进行计算时,单桩风机所受冰荷载最小,最大值约为1 900 kN.ISO给出海上风机直立圆柱冰荷载计算经验公式[23],采用ISO 规范计算得到冰厚0.2 m 下,静冰力载荷的最大值为3 000 kN,将冰荷载数值计算结果与规范结果进行对比可知,采用Matlock 模型进行计算时,计算结果与规范值较为接近.
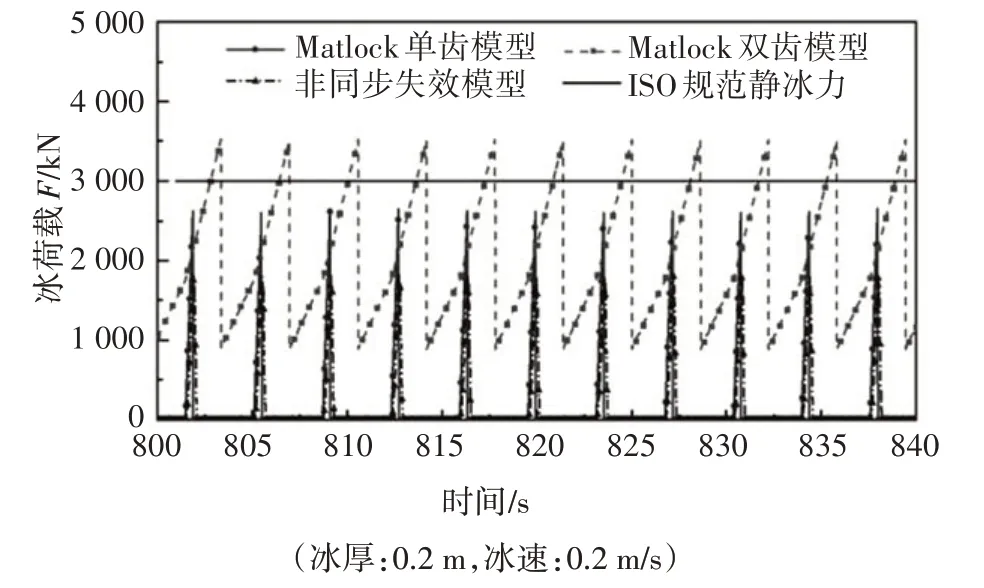
图3 不同冰载模型下的冰力时程曲线Fig.3 Comparison of ice load between different ice models(ice thickness:0.2 m,ice speed:0.2 m/s)
塔顶前后垂直于风轮平面,即来流方向.塔基、泥面线处来流方向在不同冰载数值模型下的受力特性见图4.其中,塔基、泥面线剪力以及弯矩的标准差和最大值均为除以无浮冰作用下对应的荷载的无量纲计算结果.

图4 不同冰载数值模型下塔基与泥面线位置载荷特性Fig.4 Comparison of tower base and mudline loads under differnet ice load models
如图4 所示,浮冰作用下,塔基剪力与弯矩受冰激振动影响,幅值明显增加,且波动变化更为剧烈.不同冰载数值模型塔基剪力以及弯矩受力特性具有较大差异.相比于其他冰载数值计算模型,Matlock双齿模型计算结果最大,塔基剪力与弯矩最大值分别为无浮冰作用下的2.2倍与1.3倍.
由泥面线剪力与弯矩在不同冰载数值模型下的动力响应特性可知,相较于塔基载荷特性,浮冰作用下,泥面线剪力以及弯矩受冰激振动影响更加明显,波动变化更为剧烈.由图4(b)可知,泥面线剪力以及弯矩受冰激振动作用下的标准差最大值分别为浮冰作用下的22.0倍与7.0倍,最大值分别为无浮冰作用下的5.5倍与2.0倍.与塔基载荷变化情况较为类似,采用动冰荷载计算模型时,泥面线位置处的载荷变化波动较为剧烈,易产生结构的疲劳破坏.
3.2 冰速、冰厚对结构动力响应的影响
本小节选取非同步失效数值模型,探究在不同冰速以及冰厚下,单桩海上风机受结构冰激振动的动力响应规律.图5 为结构在不同冰厚以及冰速下单桩海上风机所受冰荷载最大值.结果表明:冰荷载随冰速和冰厚的增加而增加.

图5 不同冰速以及冰厚下冰荷载最大值Fig.5 Comparison of ice load under different ice thicknesses and speeds
图6 为不同冰厚以及冰速下塔基剪力的最大值与标准差.表3、表4 分别为不同冰速以及冰厚下的塔基与泥面线位置载荷最大值与标准差统计结果.
由图6以及表3、表4可知,塔基以及泥面线位置处载荷随冰速以及冰厚的增加而不断增加.冰厚的变化对塔基与泥面线荷载的最大值影响更大.以塔基剪力为例,相同冰速下(0.2 m/s),不同冰厚塔基剪力最大值分别为:912 kN、1 070 kN、1 210 kN 以及1 350 kN,增幅分别为:17%、33%以及48%;相同冰厚(0.2 m)下,不同冰速下的塔基剪力最大值分别为:911 kN、1 070 kN、1 100 kN 以及1 180 kN,增幅分别为:17%、21%以及30%.相比于荷载最大值,不同冰速与冰厚对荷载的标准差均有较大影响.
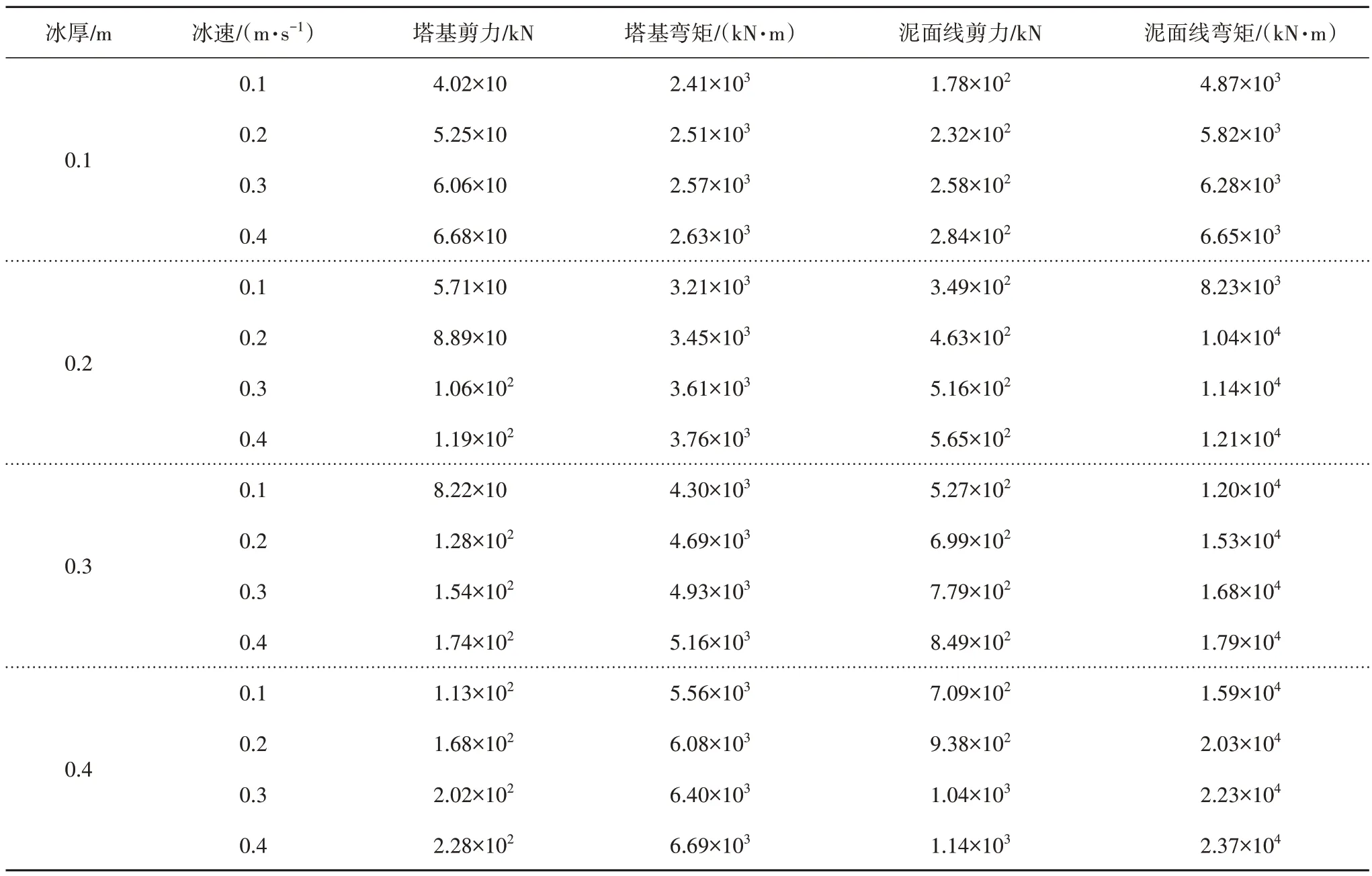
表4 不同冰速与冰厚下塔基与泥面线载荷标准差Tab.4 STD values of tower base and mudline load for different ice speeds and thicknesses

图6 不同冰速以及冰厚下塔基剪力最大值与标准差Fig.6 Comparison of maximum and STD tower base shear force under different ice thicknesses and ice speeds
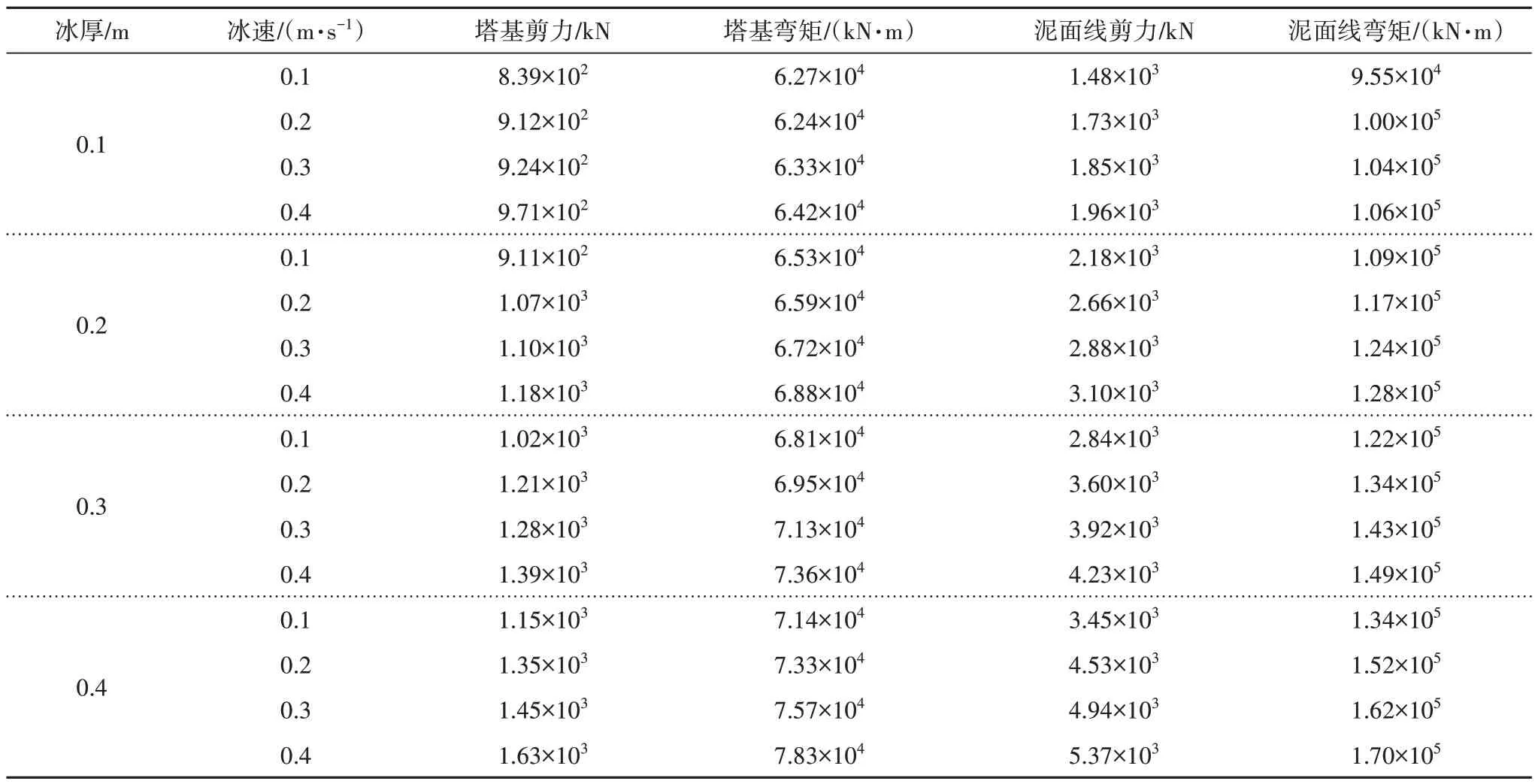
表3 不同冰速与冰厚下塔基与泥面线载荷最大值Tab.3 Maximum tower base and mudline load for different ice speeds and thicknesses
泥面线载荷较塔基载荷受冰速以及冰厚影响更大.以泥面线弯矩为例.相同冰速(0.2 m/s)下,不同冰厚泥面线弯矩最大值分别为:1.00×105kN·m、1.17×105kN·m、1.34×105kN·m 以及1.52×105kN·m,增幅分别为:17%、34%以及52%,泥面线弯矩标准差的相对增幅分别为:79%、163%以及249%.由此可见,冰荷载作用下,泥面线载荷波动较为剧烈,易引起较大的疲劳荷载.
3.3 抗冰锥结构对结构动力响应性能影响
目前,冰区海上风机常在单桩结构加装抗冰锥,使得冰荷载的破坏形式转化为弯曲破坏,从而降低作用于单桩基础结构上的冰荷载.分别采用Ralston方法[21]与Augusti 方法[24]计算作用于抗冰锥结构上的冰荷载.本小节探究采用抗冰锥结构形式单桩海上风机塔基以及泥面线位置处的载荷特性.模拟风速为11.4 m/s,冰厚0.2 m,冰速0.2 m/s.其中,抗冰锥水线面位置处直径为8 m,锥角为45°.图7 为采用抗冰锥结构塔基以及泥面线位置处载荷变化.需要注意的是,图7 所示结果为采用抗冰锥结构的动力响应值除以不采用抗冰锥结构非同步失效模型下动力响应值的无量纲最大值与标准差.

图7 采用抗冰锥结构塔基以及泥面线位置处载荷特性Fig.7 Dynamic responses of tower base and mudline using ice cone structure
结果显示:采用抗冰锥结构,由于冰的破坏形式转化为弯曲破坏后,作用于结构上的冰荷载大大减小.加装抗冰锥结构,采用两种荷载计算模型的计算结果较为接近.以Ralston 模型为例,冰荷载的最大值与标准差分别为不采用抗冰锥结构的5%与7%.由于作用于结构上的冰荷载较小,塔基以及泥面线位置处的剪力以及弯矩减小,塔基位置处剪力与弯矩最大值分别为无抗冰锥结构的82%、95%,标准差分别为无抗冰锥结构的67%与91%.相比于塔基,泥面线位置处的载荷变化更为明显,泥面线位置处剪力与弯矩的最大值分别为无抗冰锥结构的36%与81%,标准差分别为18%与65%.综上所述,采用抗冰锥结构,有益于降低塔基以及泥面线位置处的载荷响应.
4 结论与展望
本文基于FAST 耦合数值分析软件,开展了风冰联合作用下单桩海上风机动力响应分析的研究,得出如下结论:
1)冰荷载对单桩海上风机动力响应具有重要影响.以Maltock 双齿计算模型为例,考虑冰荷载作用塔基与泥面线位置处剪力与弯矩的的最大值分别为无浮冰作用下的2.2 倍与1.3 倍.与塔基位置处动力响应相比,泥面线载荷响应受冰激振动作用更为明显,波动更为剧烈.泥面线剪力与弯矩最大值分别为无浮冰作用下的5.5倍与2.0倍.同时,采用不同冰载数值模型计算结果具有一定的差别,采用Matlock 双齿模型计算结果最大.
2)结构动力响应随冰速、冰厚的增加而增加.相比于冰速参数,冰厚对结构动力响应的最大值影响更大,不同冰厚下塔基剪力最大值的增幅分别为17%、33%以及48%,而不同冰速下塔基剪力最大值的增幅分别为17%、21%以及30%.对于塔基与泥面线位置处的载荷波动,冰厚与冰速对结构的动力响应均有较大的影响.同时,泥面线载荷更易受冰激振动的影响,波动更为剧烈,需重点关注.
3)加装抗冰锥结构能有效降低结构的载荷响应.由于采用抗冰锥结构,冰的破坏形式发生变化,作用于结构上的冰荷载减小,塔基与泥面线载荷响应显著降低.塔基剪力与弯矩的最大值分别为无抗冰锥结构的82%与95%,泥面线剪力与弯矩的最大值分别为无抗冰锥结构的36%与81%.综上所述,采用抗冰锥结构,有益于降低塔基以及泥面线位置处的载荷响应.
本文忽略了极限海况等停机工况,同时忽略了桩土作用对单桩海上风机的动力响应性能的影响,还需在后续的工作中进一步研究.
