考虑楼层刚度的伸臂结构力学性能
2022-10-09陈林谭平赵啸峰徐亚飞周福霖
陈林,谭平,赵啸峰,徐亚飞,周福霖,2,3
(1.湖南大学土木工程学院,湖南长沙 410082;2.广州大学工程抗震研究中心,广东广州 510405;3.广东省地震工程与应用技术重点实验室,广东广州 510405)
带伸臂的超高层结构由于其良好的抗侧性能,是近年来应用较多的超高层结构体系,这种体系通过在设备层或避难层设置巨形梁或桁架(外伸臂)将核心筒与外框柱进行连接,使外框柱参与整体抗弯作用,从而提高结构的抗侧能力,减小水平位移,同时也相应地减少核心筒承担的底部倾覆力矩.
目前国内外学者对此种结构体系研究较多,并对其计算模型进行了平面简化以探究其受力性能.1975年Taranath[1]将带伸臂的框架-核心筒结构简化成一平面模型并忽略普通楼盖作用,经分析得出在风荷载作用下最优伸臂位置接近结构中部的结论.在此基础上,Mcnabb 和Muydi[2]验证了Taranath 的分析并进一步得出了带两道伸臂加强层结构的最优位置.1983年Boggs和Gasparini[3]研究了带一道伸臂层的变截面伸臂体系的内力和位移,进而分析了伸臂的最优位置.由于伸臂截面高度较大,即高跨比较大,为使其与实际受力情况一致,Hoenderkamp[4]在分析伸臂结构时考虑了伸臂桁架剪切变形的影响.Rahgozar等[5]采用最小势能原理推导出带伸臂筒中筒结构的简化顶点位移计算方法并考虑剪力滞后效应的影响.
张正国等[6]以深圳126层中华大厦为研究对象,采用力法推导出带多道伸臂的框架-核心筒结构顶点位移公式,并分析了影响其抗侧刚度的主要参数.黄世敏等[7]通过建立协调变形方程研究伸臂层的最优位置,同时分析了不同数量以及加强层刚度对结构的影响,从而给加强层设计提供建议.沈蒲生等[8]对设有两道加强层的变截面框架-核心筒结构的动力特性进行了分析,对加强层的最优位置、自由振动频率等各方面进行了详尽的分析.Chen 等[9]提出了消能伸臂结构的简化计算分析模型,并对影响参数如最佳伸臂位置、最优阻尼比等进行了分析,但忽略了外框架柱轴向刚度的影响.邓仲良等[10]分析了含单伸臂的框架-核心筒简化模型的力学性能并利用有限元法进行验证.方娥[11]将多道伸臂结构简化为平面模型,考虑伸臂刚度影响并将普通楼层梁简化为均布在整个楼层高度的连续杆,按最小势能原理推导出多道伸臂结构的侧移计算公式,得出不同刚度加强层受力性能差异,但未讨论普通楼层刚度及数量对整体刚度的影响.Tan等[12-13]采用等效扭转刚度模拟外框柱、伸臂以及阻尼器连接的刚度并提出了消能伸臂结构的简化动力计算方法.汪梦甫等[14]运用数值模拟方法研究了带伸臂减震层的超高层结构的抗风性能.周颖等[15]通过振型反应谱法分析了伸臂结构的最优伸臂位置并与静力分析结果进行对比.
上述研究基本都将带伸臂的框架-核心筒结构简化为一平面模型并忽略普通楼层梁板对结构的影响,将核心筒简化为一欧拉梁,此简化模型受力清晰,计算简单,但忽略了普通楼层梁板对整体刚度贡献大小.由于伸臂结构普通楼层数量多,考虑楼板对梁刚度贡献后,其连接外框架柱与核心筒的梁抗弯刚度不容忽视,其对结构整体抗侧刚度有较大影响进而影响结构动力特性.因此,有必要考虑普通楼层梁板刚度对其结构力学性能的影响规律进行研究,提高结构方案设计精度.在前人研究的基础上,本文考虑普通楼层刚度后对带伸臂的框架-核心筒结构进行分析,研究各参数对整体抗侧刚度影响规律,提出考虑普通楼层刚度等效核心筒附加刚度比计算公式.结合工程实例,对比分析简化计算模型与有限元模型的静力、动力计算结果.
1 基本假定
前述文献中对带伸臂的框架-核心筒进行分析时,假定核心筒与外框柱截面沿楼高保持不变,将核心筒简化为欧拉梁即仅考虑其弯曲变形,核心筒与外框架仅由伸臂连接,忽略楼盖与楼层梁作用,并将外框柱简化为轴心受力构件.本文在已有研究基础上,以单道伸臂位于结构顶部(可视为多道伸臂子结构)为例着重研究伸臂结构的力学性能及动力特性,基本假定如下:
1)结构处于线弹性状态,不考虑结构P-Δ效应;
2)核心筒简化为欧拉梁,不考虑其剪切变形及扭转变形;
3)因外框柱抗弯刚度远小于核心筒抗弯刚度,外框柱假定为轴心受力构件;
4)考虑伸臂的弯曲变形及剪切变形;
5)外框柱及核心筒剪力墙截面沿建筑高度不变;
6)考虑普通楼层梁板的影响,楼层梁与核心筒刚接,与外框柱近似铰接但提高其线刚度.
2 伸臂结构力学性能
2.1 未考虑楼层刚度计算模型
未考虑普通楼层的单伸臂结构简化模型如图1(a)所示,核心筒抗弯刚度为EI,伸臂抗弯刚度为EaIa,剪切模量Ga=0.42Ea[6],外框架柱轴向刚度为EcAc,伸臂梁或桁架高度为h,外框柱与核心筒中心间距为r,核心筒边缘距外框柱中心为b,a=r-b,结构总高度为L,沿建筑高度承受倒三角荷载qT、均布荷载qD、集中荷载Fp,Ma为伸臂对结构产生的反向弯矩,X轴为楼层方向,Y轴为水平位移方向.
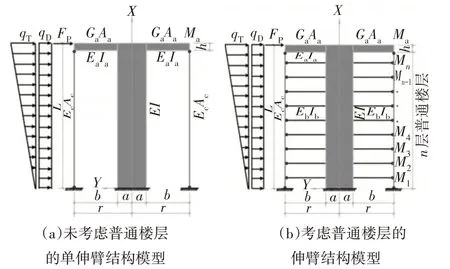
图1 伸臂结构简化模型Fig.1 Simplified model of outrigger structure
2.1.1 外伸臂的转角计算
外伸臂处的转角θ0等于外框柱轴向变形引起的转角θc、剪切变形产生的转角θg以及伸臂弯曲产生的转角θb之和[4],如图2所示.
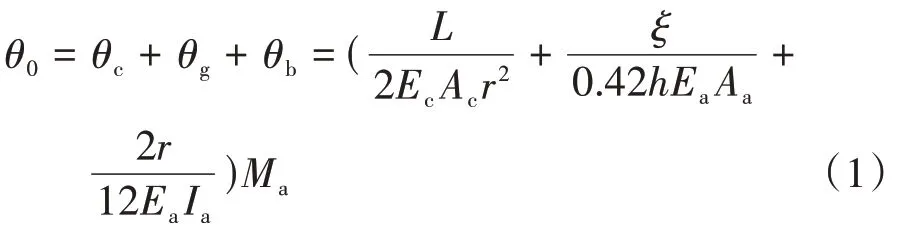

图2 伸臂变形示意图Fig.2 Schematic diagram of outrigger deformation
式(1)定义跨度比ξ=b/r,Ma为伸臂提供的反向弯矩.令无量纲参数外框柱刚度比Pc=EI/(2EcAcr2),伸臂刚度比Pa=2EIr/(EaIaL),伸臂高跨比γ=h/r,则式(1)可简化为:

2.1.2 核心筒在伸臂位置转角计算
1)倒三角荷载作用下核心筒转角计算

2)均布荷载作用下核心筒转角计算

3)集中荷载用下核心筒转角计算
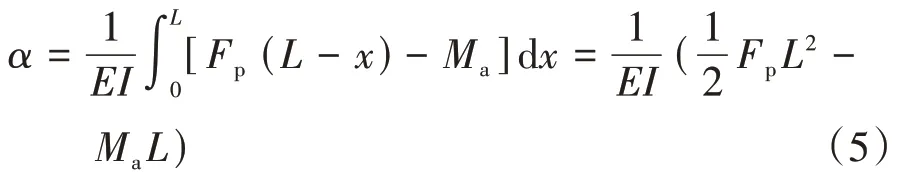
因伸臂的转角等于相应位置核心筒处的转角,即θ0=α,故

2.1.3 顶点位移计算
1)倒三角荷载作用下顶点位移计算
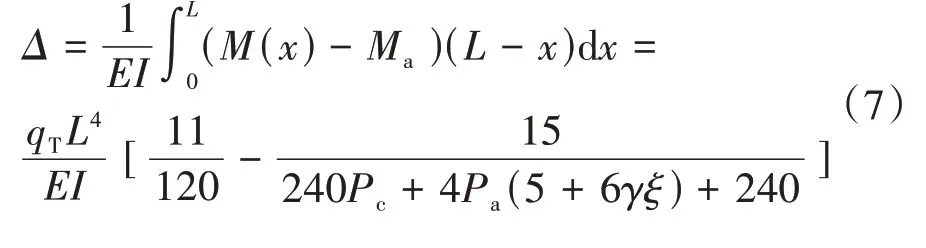
式中:M(x)为未加伸臂时核心筒作为悬臂欧拉梁沿X轴承受的弯矩.
2)均布荷载作用下顶点位移计算
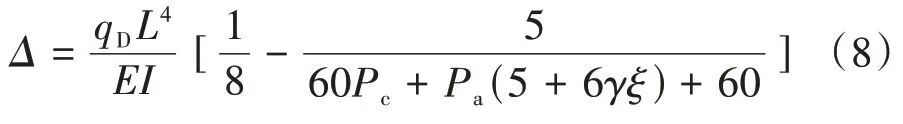
3)集中荷载作用下顶点位移计算
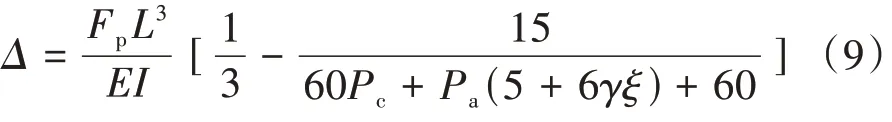
2.2 考虑楼层刚度计算模型
普通楼层假设为n层(即结构总共n+1层),各层层高相等,普通楼层梁抗弯刚度均为EbIb(考虑楼板对梁刚度贡献).普通楼层梁截面高度较小,忽略其剪切变形.与伸臂梁位置不同的是外框柱连接位置不能完全视为铰接,因为外框柱对普通楼层梁有较大约束,为减小计算工作量,将普通梁刚度进行简化:忽略外框柱抗弯刚度,普通梁与外框柱近似铰接,但提高其线刚度,为(4EbIb/b+2EbIb/b),普通楼层梁对结构的反向弯矩为Mn,如图1(b)所示.
2.2.1 楼层位置梁及伸臂转角计算
类似2.1 节,第n层梁对核心筒提供的抵抗力矩为

式中:Fcn为第n层梁对外框柱作用力.
第n层梁与第n-1层梁间外框架柱轴向变形为
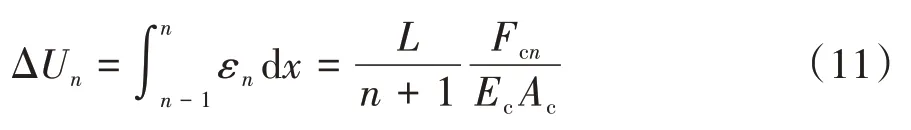
普通楼层梁与核心筒刚接,与框架柱近似铰接,普通楼层梁弯曲变形产生的转角
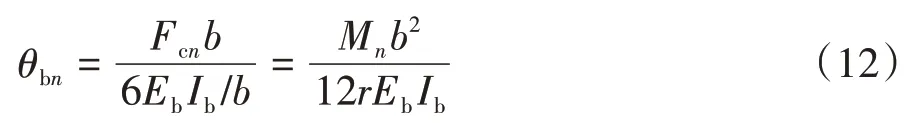
在普通楼层位置,由变形协调条件
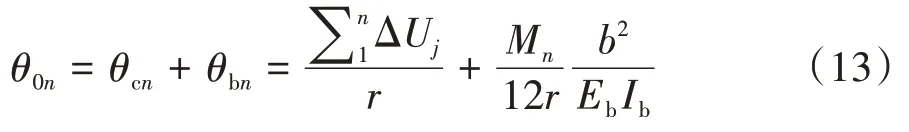
式中:ΔUj表示第j层梁与第j-1层梁间外框架柱轴向变形.
改写成矩阵形式如下:
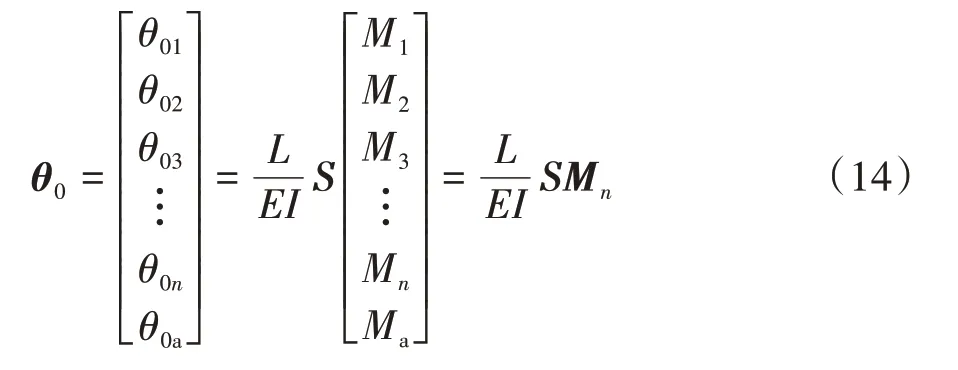
其中,

式中:Pb=2EIr/(EbIbL),定义为普通楼层梁刚度比.
2.2.2 核心筒在普通楼层梁及伸臂位置转角计算

将上述公式进行整理得:
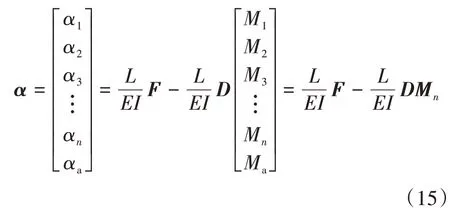
其中,
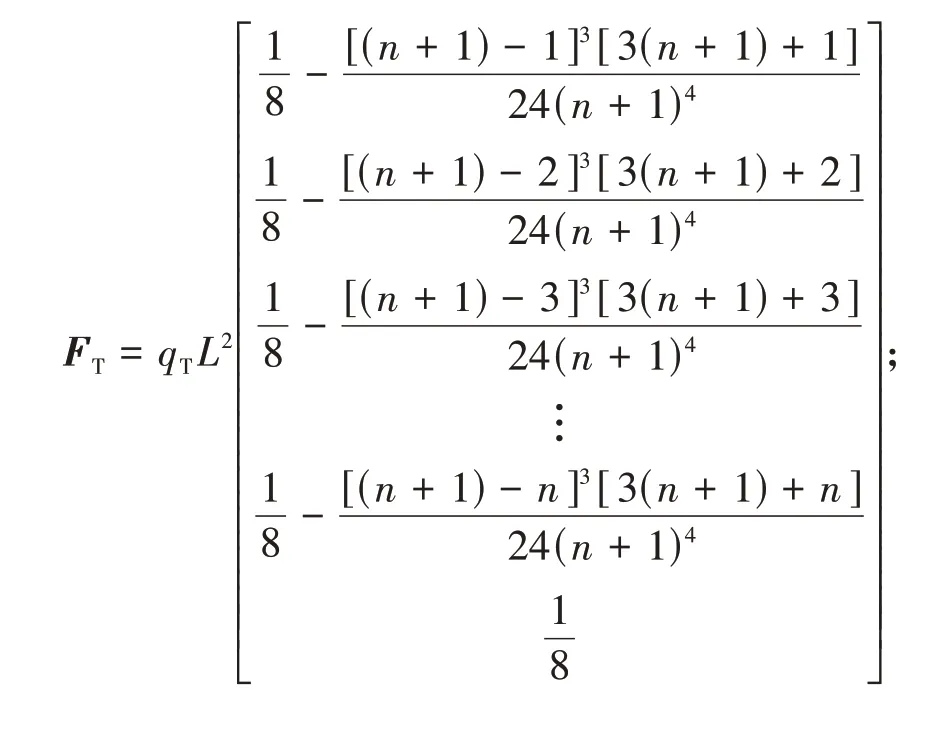

式中:FT、FD、FC分别对应在倒三角荷载、均布荷载以及集中荷载作用下的荷载矩阵;F,D为与普通楼层数n相关的常数矩阵.因θ0=α,可求出Mn.

式中:B=S+D.
2.2.3 顶点位移计算
1)倒三角荷载作用下顶点位移计算

2)均布荷载作用下顶点位移计算
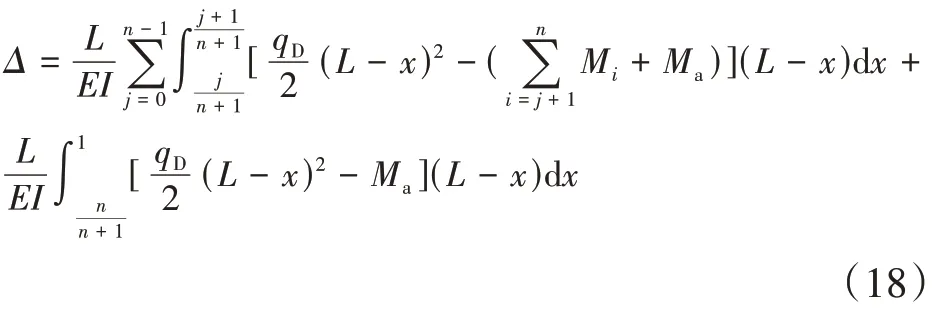
3)集中荷载作用下顶点位移计算

2.3 本文提出模型与未考虑楼层刚度模型对比
以一实际超高层结构简化模型为例进行分析,对比考虑普通楼层刚度后结构顶点位移大小及楼层水平位移曲线形态变化.建筑所在地区抗震设防烈度为7 度,场地类别为Ⅱ类,基本风压为0.35 kN/m2,高度L=200 m,层数总共为50 层,r=19 m,b/r=0.526,假定风荷载沿建筑高度为倒三角荷载模式且qT=30 kN/m,核心筒墙厚为800 mm,EI=1.4×1013N·m2;外框架柱截面尺寸为1 800 mm ×1 800 mm,EcAc=1.2 × 1011N;伸臂梁位于结构顶部,h/r=0.21,EaIa=1.3 × 1011N ⋅m2.
图3 所示为本文计算方法与未考虑普通楼层简化计算方法对比图,横坐标为楼层水平位移δ,纵坐标为对应楼层位置.分别取普通楼层梁刚度比Pb=10 000 及Pb=100 000 进行计算,可以看出当普通楼层梁刚度比Pb增大,即普通楼层梁刚度减小时,结构楼层水平位移δ曲线更接近未考虑普通楼层计算结果.当Pb=10 000 时,相对未考虑楼层刚度时顶点位移小10%;当Pb=100 000,即普通楼层梁刚度趋向0时,相对未考虑楼层刚度时顶点位移小1.1%,其变形曲线基本与未考虑普通楼层计算曲线重合,说明本文提出的考虑普通楼层计算方法能退化至未考虑普通楼层刚度情况,故本文所提出的计算方法更具普适性.

图3 本文计算方法与未考虑普通楼层计算方法对比Fig.3 Results of the paper compared without considering ordinary floors
3 有限元验证
以某实际超高层结构为例建立平面有限元模型,考察其顶点位移大小及楼层水平位移曲线形态,并与本文提出方法计算值进行比较,以验证本文假定及提出方法的有效性.本节有限元算例参数同2.3节.
3.1 伸臂结构有限元计算模型
平面有限元计算模型如图4 所示,普通层楼梁截面尺寸为350 mm×700 mm,考虑楼板对梁刚度影响后EbIb=4.3 × 108N·m2;其余构件信息及荷载信息同2.3 节.外框柱及梁采用ETABS 中的框架单元,剪力墙采用壳单元,建立平面模型,采用ETABS软件分别计算未考虑普通楼层、普通楼层梁与外框柱铰接及普通楼层梁与外框柱刚接3种工况.
1.1 材料 MDA-MB-231细胞系购自上海细胞研究所细胞库。B7-H3真核表达载体pcDNA3-B7-H3由东北师范大学药物基因和蛋白筛选国家工程实验室构建。p27、cyclinA和cyclinE抗体均购自Santa 公司,抗B7-H3抗体购自RB公司,抗GAPDH抗体购自上海康成生物有限公司,HRP标记的第二抗体购自北京鼎国昌盛生物技术有限公司。ECL发光试剂盒购于全式金公司。BrdU试剂盒购自Roche公司。细胞周期与细胞凋亡检测试剂盒购于碧云天生物技术研究所。

图4 有限元模型Fig.4 The FEM of the structure
3.2 有限元计算结果对比
图5 所示为本文计算方法与有限元方法计算的结构楼层水平位移δ曲线对比结果,可以看出,未考虑普通楼层梁刚度时顶点位移最大,采用2.1节方法计算时顶点位移为246.14 mm,相对楼层梁两端刚接有限元模型(实际结构模型,顶点位移为182.50 mm)误差率为34.9%,对整体抗侧刚度影响较大,在具体方案设计时不能忽视.本文提出的计算方法顶点位移为209.70 mm,相对梁两端刚接有限元模型误差率为14.9%,误差率相对未考虑普通楼层梁刚度情况减小20%.

图5 本文计算方法与有限元结果对比Fig.5 Results of FEM compared with the method in the paper ordinary floors
本文提出的计算方法假定外框架柱为轴心受力构件,忽略外框架柱抗弯刚度的影响,虽外框架柱抗弯刚度相对核心筒抗弯刚度可忽略不计,但对整体结构抗侧刚度有一定的贡献;同时结构简化模型中虽对楼层梁与外框架柱连接方式做了近似等效处理,但与实际楼层梁和外框架柱刚接连接方式有一定差别且等效楼层梁线刚度小于实际刚接连接方式.基于以上两点,顶点位移略大于有限元分析结果但小于楼层梁与外框柱铰接计算结果,即介于楼层梁与外框柱刚接与铰接之间,误差率已大大优于未考虑普通楼层情况,其有效性优于2.1节计算方法并能满足方案设计要求.
4 伸臂结构参数分析
4.1 伸臂与楼层梁刚度比的影响
为探究伸臂刚度与普通楼层梁刚度比对整体抗侧刚度的影响,以倒三角荷载模式为例,令普通楼层刚度比μ=EaIa/(EbIb)=Pb/Pa,假定Pc=0.1,普通楼层数量n=19~49,顶点位移Δ的单位为qTL4/EI.由图6 可看出,结构顶点位移Δ随μ增大而增大,伸臂刚度相对普通楼层梁刚度越大,结构整体抗侧刚度越小,即μ增大时,伸臂提供的整体结构抗侧刚度占比越大,普通楼层梁对整体刚度的贡献越小.当μ为0~200时,整体刚度变化较明显,当μ增大到300以上时,整体抗侧刚度变化趋于稳定,即普通楼层梁对整体刚度的贡献趋于稳定.从图6 中也可以看出,当普通楼层数量增加时,顶点位移Δ减小,即结构整体刚度增加.
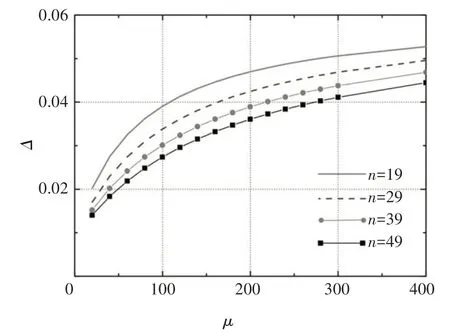
图6 普通楼层数量n及伸臂与楼层刚度比μ的影响Fig.6 Influence of n and μ
4.2 伸臂间楼层数及楼层刚度比影响
假定结构处于合理设计范畴,令外框柱刚度比Pc=0.1,伸臂刚度比Pa=10,跨度比ξ=0.4,伸臂高跨比γ=0.2,顶点位移单位为qTL4/EI.图7所示为普通楼层刚度比Pb及普通楼层数量对整体抗侧刚度影响,从图中可看出,顶点位移随伸臂间普通楼层数量n增加而减小,即整体抗侧刚度随n增加而增大.普通楼层刚度比Pb对顶点位移有显著影响,整体抗侧刚度随Pb增大(普通楼层梁刚度减小)而减小,当Pb增大到一定程度时,整体抗侧刚度随楼层数量的增加由非线性下降变为直线下降,即当普通楼层梁刚度减小到一定程度时,楼层数量对整体抗侧刚度的影响降低.

图7 普通楼层梁刚度比Pb及普通楼层数量n的影响Fig.7 Influence of Pb and n
4.3 外框柱刚度比及伸臂刚度比的影响
令Pa=10,Pb=2 000,ξ=0.4,γ=0.2.从图8可看出,顶点位移随伸臂间普通楼层数量增加而减少,即刚度增大,两者近似呈线性关系.整体抗侧刚度随Pc增加而减小(随外框柱轴向刚度减小而减小),当Pc增加到5 时,伸臂间楼层数量对抗侧刚度影响较小,即主要由核心筒提供抗侧刚度.
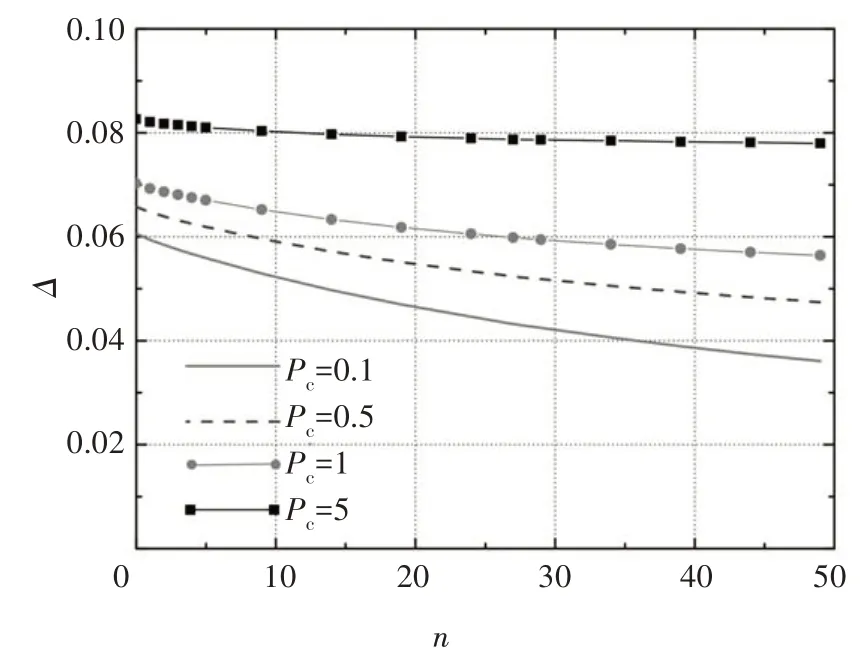
图8 外框柱刚度比Pc及普通楼层数量n的影响Fig.8 Influence of Pc and n
当Pc=0.1,Pb=2 000,ξ=0.4,γ=0.2 时,从图9 可看出,随着伸臂刚度比Pa增加(伸臂抗弯刚度减小),结构整体抗侧刚度减小,当Pa>20 时,Pa对整体抗侧刚度影响显著降低.当伸臂刚度增加到一定程度时(Pa接近0),普通楼层数量对整体抗侧刚度几乎无影响,水平构件主要由伸臂提供刚度.
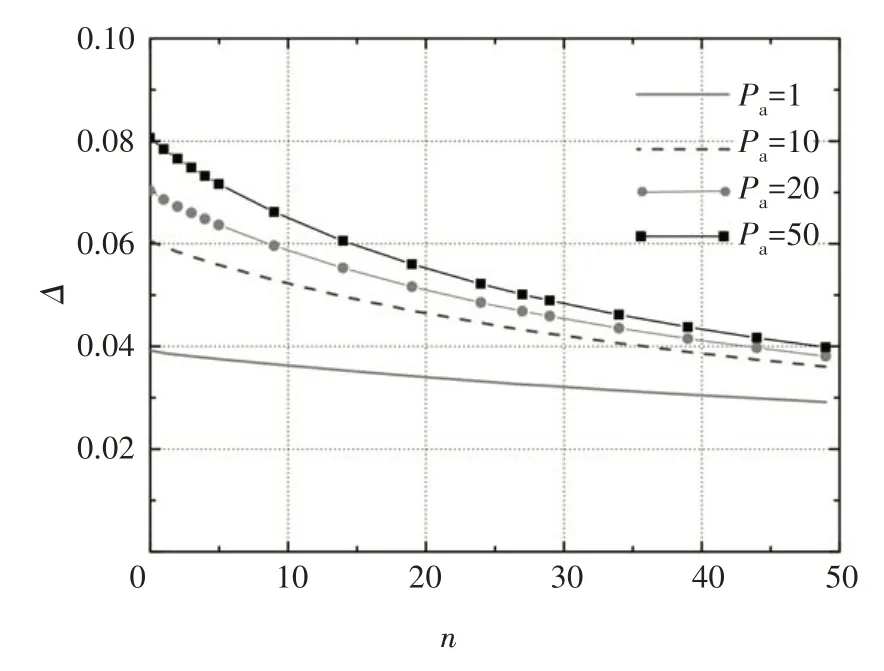
图9 伸臂刚度比Pa及普通楼层数量n的影响Fig.9 Influence of Pa and n
4.4 伸臂跨度比与高跨比的影响
图10 所示为伸臂跨度比对整体抗侧刚度的影响,从图中可看出,ξ的变化对结构顶点位移影响较大,整体抗侧刚度随ξ的增大而减小.在具体结构设计中,ξ一般为0.4~0.6,可根据建筑功能布置综合考虑.从图11可以看出,高跨比γ对结构整体刚度影响不明显,反映出剪切变形在结构整体变形中所占比例不大,但考虑剪切变形的影响降低了结构整体抗侧刚度.

图10 普通楼层数量n及伸臂跨度比ξ的影响Fig.10 The influence of n and ξ

图11 普通楼层数量n及伸臂高跨比γ的影响Fig.11 The influence of n and γ
5 考虑楼层刚度简化分析方法
5.1 等效核心筒刚度比
从第3、第4 节分析中可看出,考虑普通楼层刚度的影响后伸臂结构整体刚度的模型计算结果较为准确,且普通楼层刚度比Pb、普通楼层数量n、伸臂刚度比Pa、外框柱刚度比Pc、跨度比ξ以及伸臂高跨比γ均对整体结构抗侧刚度有不同程度的影响.但考虑普通楼层刚度后增加了大量自由度,提高了在结构方案设计中的计算工作量,为简化计算,遂以等效核心筒刚度比β来估算普通楼层对整体的抗侧刚度的影响.实际进行方案设计时,简化模型可仅考虑伸臂梁或桁架刚度,通过β值将核心筒刚度等效提高.即:模型计算时,去掉普通楼层后伸臂结构的顶点位移应与考虑普通楼层刚度影响相等,并将此影响提高的抗侧刚度等效附加于核心筒,即β=(EI)eq/EI,在倒三角荷载用下公式可表达如下:

同理可求出在均布荷载及集中荷载下等效核心筒刚度比分别为:

图12所示为3种荷载模式下等效核心筒刚度比数值.从图中可看出,随着各影响参数变化,3 种荷载模式下等效核心筒刚度比数值基本一致,倒三角荷载模式与均布荷载模式变化曲线基本重合,顶部集中荷载作用下等效核心筒刚度比数值与前两者最大相差1.1%,由此可知,荷载模式对等效核心筒刚度比影响甚微,可忽略.
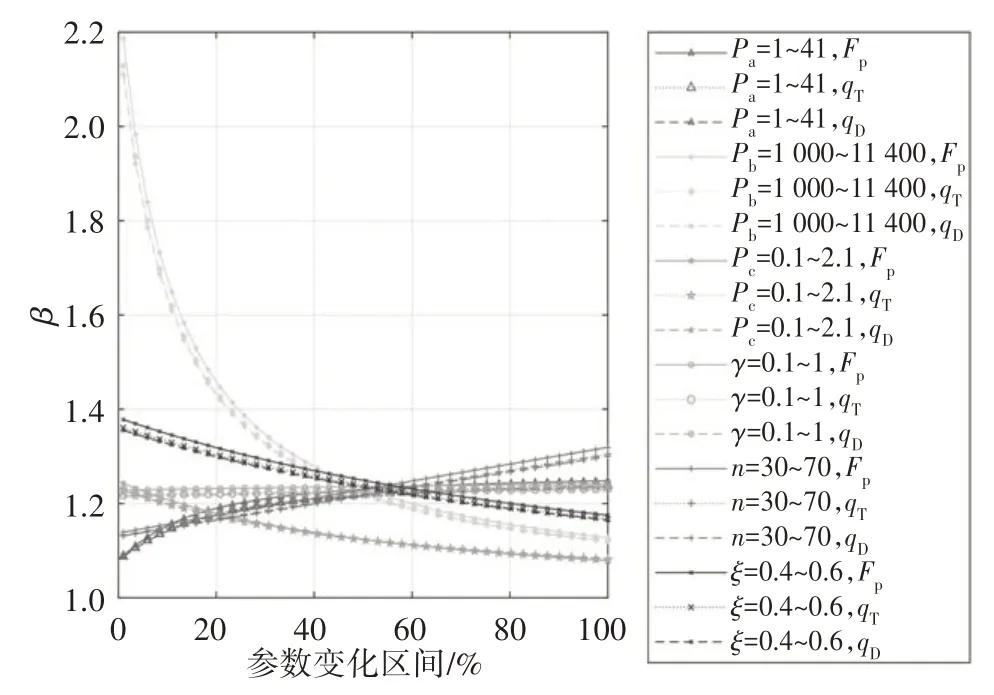
图12 荷载模式对等效核心筒刚度比的影响Fig.12 The influence of load mode on equivalentcore tube stiffness ratio
5.2 等效核心筒刚度比拟合公式
为分析各参数变化对等效核心筒刚度比的影响,以倒三角荷载模式为例,选取各参数变化区间:1 ≤Pa≤50,1 000 ≤Pb≤6 000,0.1 ≤Pc≤5,0.4 ≤ξ≤0.6,0.1 ≤γ≤1,20 ≤n≤60,采用斯皮尔曼等级相关系数ρ表示参数相关性的强弱.斯皮尔曼等级相关系数取正值时,参数和等效核心筒刚度比或伸臂结构抗侧刚度成正相关,反之则为负相关,计算公式如下:
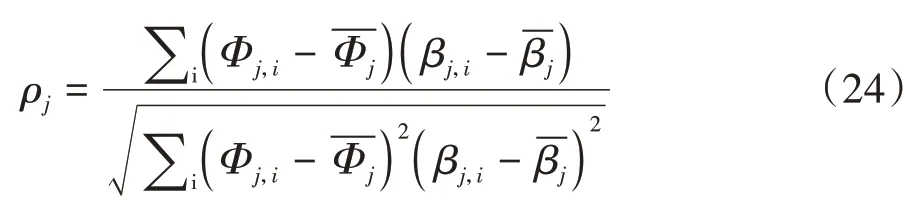
式中:Φ=[Pa,Pb,Pc,ξ,γ,n];j为参数数量;i为各参数的变化数量,计算时分别取参数各变化区间的10 等分点进行计算,参数变化的组合数量为116.
从图13 中可知,外框柱刚度比Pc和β或Δ的斯皮尔曼等级相关系数取值分别为0.91、-0.82,Pc和β或Δ的相关性最为显著,分别成负相关或正相关;普通楼层数n、普通楼层梁刚度比Pb和伸臂刚度比Pa和β或Δ的斯皮尔曼等级相关系数绝对值(|ρ|)取值范围为0.3~0.4,相关性一般;此外,ξ和γ对等效核心筒刚度比或伸臂结构抗侧刚度的影响较小.在各参数取值区间内,对取值为1.0~1.35 的等效核心筒刚度比和各参数进行多项式非线性最小二乘法的函数拟合,拟合函数详见公式(25)及表1.
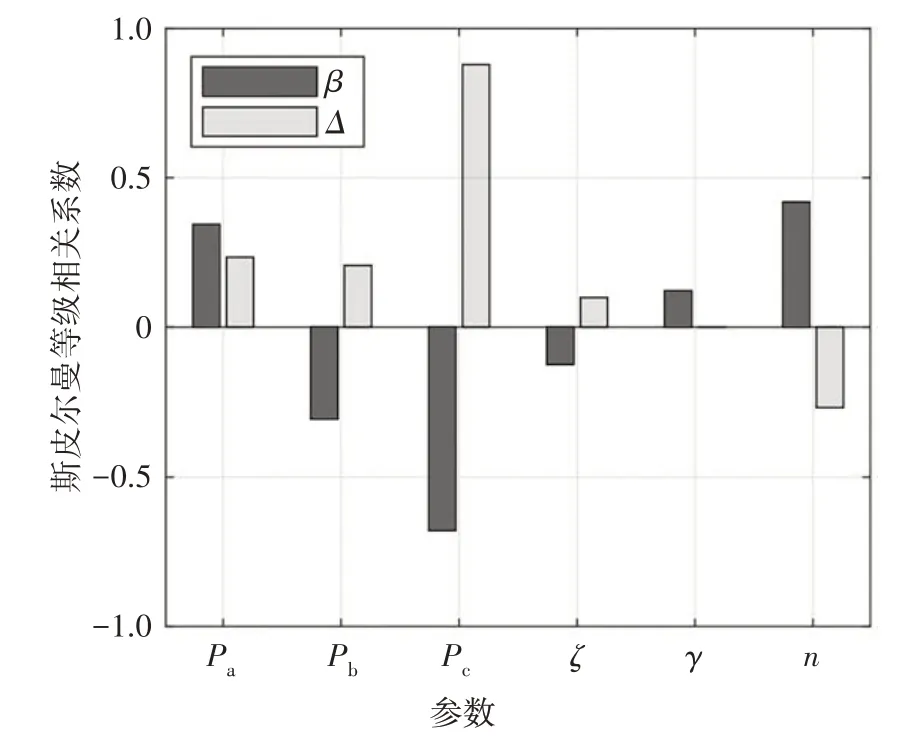
图13 各参数对β及Δ的相关性图Fig.13 Correlation of each parameter to β and Δ

表1 公式(25)的各参数数值Tab.1 The parameter values of formula(25)
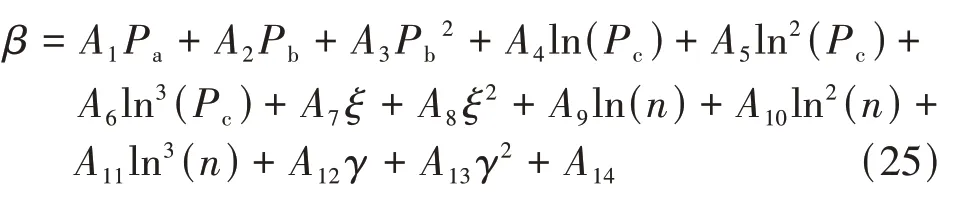
图14中横坐标为文中简化计算方法计算值,纵坐标为公式(25)计算值,拟合方程决定系数R2接近0.92,均方根误差(RMSE)约为0.02,公式(25)基本能反映出实际简化计算方法值.以第3 节算例为例,公式(25)计算值与采用本文提出方法计算值吻合较好.

图14 计算值与公式(25)对比图Fig.14 Comfarison chart between calculated value and formula(25)
从表2可看出,第3节算例中公式值与计算值吻合较好,误差率为1.7%,说明公式(25)计算β值准确率较高.

表2 计算值与公式(25)对比表Tab.2 Comparison table between calculated value and formula(25)
6 简化前后动力特性对比
伸臂结构考虑普通楼层刚度后整体刚度有所增加,故采用未考虑普通楼层简化模型对其动力特性进行分析时,会低估结构整体刚度,周期增大,地震力减小,偏不安全.但实际方案设计时,仅考虑伸臂结构刚度进行结构分析时能大大减少计算工作量,采用本文所提出的等效核心筒刚度比方法能在简化计算的同时提高方案设计精度.
文献[16]给出了带单道伸臂的框架-核心筒结构的基频估算公式,但未考虑普通楼层对整体刚度的影响.

式中:EI为核心筒抗弯刚度;m为结构总质量;ω为基频估算值;H为结构总高度.
根据前文等效核心筒刚度比概念,将提高的抗侧刚度等效附加在核心筒上,即用(βEI)替代公式(26)中核心筒抗弯刚度可求出考虑普通楼层后的结构基频.
以第3 节算例为例,对比结构动力特性计算结果.由表3 可看出,未考虑普通楼层刚度自振周期明显偏大,经本文方法修正后,能大大减少仅考虑伸臂层刚度进行动力分析时的误差.在实际结构方案设计时,经本文等效核心筒刚度修正后,能采用仅考虑伸臂刚度简化模型进行动力分析.
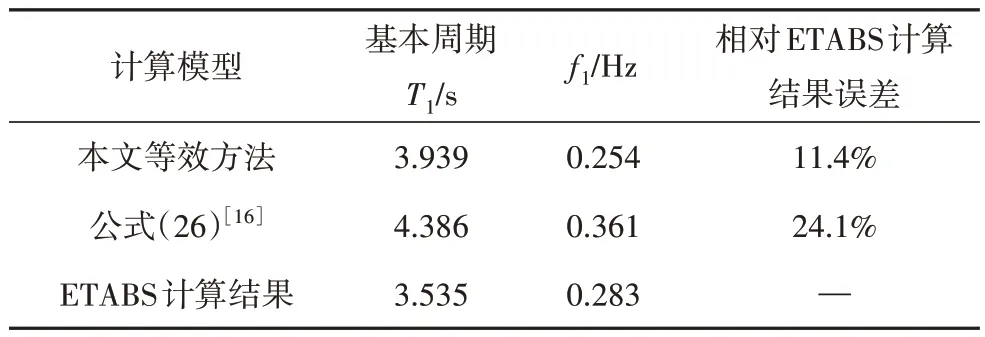
表3 动力特性对比Tab.3 Comparison of the dynamic properties
7 结论
本文对考虑普通楼层刚度的伸臂结构力学性能进行了研究,并结合工程算例对比分析了有限元模型的静力、动力计算结果,主要结论如下:
1)针对带伸臂的框架-核心筒结构提出考虑普通楼层刚度的简化计算模型,推导出顶点水平位移计算方法,其与有限元计算结果吻合较好,相对未考虑普通楼层刚度情况误差率减小20%.
2)以简化模型为基础提出了等效核心筒刚度比概念,根据参数分析结果拟合出等效核心筒刚度比计算公式,其能较好地估计普通楼层对伸臂结构的刚度贡献.
3)将等效核心筒刚度比运用于动力分析中能近似估计考虑楼层刚度伸臂结构的基本周期.
4)分析了各参数对结构整体抗侧刚度的影响规律,随着伸臂与普通楼层刚度比μ增大,即伸臂提供的整体结构抗侧刚度占比越大,普通楼层梁对整体刚度的贡献越小,伸臂结构整体抗侧刚度降低;随着普通楼层数量n增大,伸臂结构抗侧刚度提高,当普通楼层梁刚度减小到一定程度时,楼层数量n对整体抗侧刚度的影响降低.
