循环荷载下桩承式路堤中土拱效应动力折减系数离散元研究

崔晓艳，庄妍，张希栋，胡顺磊，程欣婷

（1.混凝土及预应力混凝土结构教育部重点实验室（东南大学），江苏南京 211189；2.东南大学土木工程学院，江苏南京 211189；3.太原理工大学土木工程学院，山西太原 030024；4.河海大学土木与交通学院，江苏南京 210098；5.南京工业大学交通运输工程学院，江苏南京 210009）

土拱效应的形成条件和荷载传递机理是桩承式路堤中桩-土协同作用的关键性科学问题.如赵明华等［1］基于建立的双等沉面荷载传递模型分析了路堤-桩-土间的协调变形作用.实际工程中，路堤表面还存在交通荷载的循环作用，其在交通荷载下的动力响应特性将直接影响路堤的承载能力及稳定性.目前针对桩承式路堤的研究主要侧重于静力荷载作用，动力荷载作用下的土拱效应研究尚处于起步阶段.

Heitz 等［2］基于动力模型试验，分析了循环荷载作用下路堤中的应力分布规律以及加筋体对结构承载力的影响，并根据试验结果提出了应力折减系数的概念，但没有给出该系数的解析表达式.Van Eekelen等［3］通过现场试验发现：在交通荷载作用下，路堤中的土拱效应呈减弱趋势.研究者也发现循环荷载作用下路堤的荷载传递效率比静载下的低，且随循环次数增加而呈减小趋势，最后趋于稳定［4］.许朝阳等［5］采用可视化的模型试验，对比分析了静、动载作用下桩承式路堤工作机理、应力传递和变形性状，研究了动载作用下路堤高度、桩距、荷载频率等因素对路堤承载力的影响.Han等［6］通过室内模型试验分析了不考虑软土与土工格栅情况下路堤中的动应力分布.试验结果表明，在动载作用下土拱首先从拱脚处破坏，然后发展到拱顶破坏.毕宗琦等［7］基于Hewlett 和Randolh［8］提出的等厚半圆理论土拱分析模型，推求了循环荷载作用下软土上方和桩帽上方的竖向应力.Dong等［9］与Pham等［10］分别基于模型试验以及数值模拟研究结果发现：动力荷载作用下桩承式路堤中的土拱效应发生了衰减，循环荷载作用下路堤的荷载传递效率比静载下的低，且随循环次数的增加而呈减小趋势，最后趋于稳定.魏平［11］采用可视化模型试验分析了路堤高度、动力荷载频率和幅值等对桩承式低填方路堤中土拱效应的影响规律.Wang等［12］基于高铁荷载作用下桩承式加筋路堤的足尺模型试验，提出了桩承式加筋路堤中静、动应力的计算方法.

以上研究主要基于模型试验，近年来，国内外学者采用离散元颗粒流分析软件从微观角度对动力荷载作用下桩承式路堤中的土拱效应进行分析.赖汉江等［13］研究了循环动载作用下低填方桩承式路堤中土拱效应的发挥情况.赖汉江［14］还分析了加载频率为1 Hz、100个加载周期循环内桩承式路堤中土拱效应的演变规律，主要从接触力分布规律（微观角度）与荷载传递效率（宏观角度）两个角度分析了循环荷载作用下土拱效应的发挥作用.但以上离散元数值模拟分析中，考虑循环荷载的加载频率与振幅对土拱效应影响的研究不足，因而需进一步开展相关方面的研究.

本文将基于室内模型槽试验建立桩承式路堤的离散元颗粒流模型，运用该模型分析循环动载作用下桩承式路堤中土拱效应发展演变过程与衰减规律，进而推求土拱效应动力折减系数的表达式.

1 离散元数值模型建模与参数选取

基于平面应变室内模型试验建立循环动力荷载作用下桩承式路堤的离散元颗粒流模型，并通过对路堤填料进行双轴试验，及对桩间软土进行单轴压缩试验反演获得路堤与桩间软土材料的微观参数.

1.1 室内模型试验装置简介

试验模型槽的尺寸为0.9 m×0.9 m×1.3 m（长×宽×高）.该模型试验中，采用钢制桩墙模拟桩，软土采用泡沫颗粒模拟以分析平面土拱效应的产生机理，如图1 所示.其中桩墙高为0.40 m，桩墙宽a为0.05 m，桩心间距s取值范围为0.25～0.30 m.左右桩墙与模型槽边界的距离为s/2.该室内模型试验过程及试验结果详见参考文献［15］.

1.2 桩承式路堤颗粒流数值模型建立

考虑对称性，选取图2 中虚线框所在区域，采用PFC 数值分析软件建立桩承式路堤平面应变离散元颗粒流数值模型.该模型的宽度为1 个桩心间距，即s=250 mm，模型的高度为900 mm，如图3 所示.模型槽及桩墙均采用Wall 单元模拟，路堤填料及桩间软土均采用线性接触模型Disk 颗粒模拟；路堤按照分层压实的方法进行填筑，分层填筑厚度为100 mm（与室内模型试验过程一致）.

图2 平面应变室内模型试验横截面示意图Fig.2 Cross section of the experimental device in plane strain condition

对于静载作用下桩承式路堤中的土拱效应研究，采用伺服机制在路堤顶面分级施加静载.对于循环荷载作用下桩承式路堤中土拱效应衰减规律的研究，用Clump 单元建立铺面结构来模拟刚性加载板（如图3 所示），并通过刚性加载板在路堤表面施加正弦波循环荷载，如图4所示.

图3 桩承式路堤颗粒流数值模型Fig.3 The DEM model of piled embankment

图4 静载及循环荷载施加示意图Fig.4 The static and cyclic loading used in the PFC2D model

1.3 模型参数确定

离散元模型中的计算速率依赖于模型颗粒总数，为获得较为理想的计算时间，大量学者均采用放大粒径的方法来减少颗粒的数量［16-18］.本文建立的桩承式路堤PFC2D 模型中，借鉴赖汉江［14］提出的方法，将路堤填料颗粒粒径基于试验用砂颗粒级配曲线放大3倍（如图5所示），尽量减小“尺寸效应”对计算结果的影响.

图5 路堤填料颗粒级配Fig.5 The grading diagram of embankment material

在离散元模型中，材料细观参数的选取基于相应的宏观指标反演试算确定.路堤填料颗粒细观参数基于试样尺寸为39.1 mm×80 mm（宽×高）的数值对双轴试验与室内三轴试验结果进行反演试算.其过程简述如下：

1）根据放大后的颗粒粒径级配曲线及孔隙率，生成尺寸为39.1 mm×80mm（宽×高）的试样，循环至平衡状态；

2）使用伺服机制在试样四周的墙体分别施加10 kPa、20 kPa、40 kPa围压，并循环至平衡状态；

3）围压加好后，对试样的上下墙体赋予恒定的速度，对试样进行加载，并记录加载过程中相应的数据以绘制成应力-位移曲线.

图6 所示为数值双轴试验与三轴试验应力-应变曲线结果对比图.经过不断调试参数，直到数值模拟结果与三轴试验结果基本相同，最终确定路堤填料细观参数详见表1.

图6 数值双轴试验应力-应变曲线Fig.6 The stress-strain curve of biaxial test for embankment material

桩间软土颗粒细观参数采用尺寸为250 mm ×300 mm（宽×高）的数值压缩试验反演试算确定.具体步骤为：通过对数值试样顶部的加载板施加恒定速度进行加载，并记录加载过程中加载板所受到的竖向应力及位移变化（如图7 所示），不断调试桩间土颗粒的细观参数.其中，桩间土试样的颗粒粒径为0.8～1.0 mm 且服从标准正态分布，最终确定桩间土颗粒细观参数如表1所示.

表1 PFC模型微观参数Tab.1 The microcosmic parameters of the PFC model

图7 桩间土单向压缩试验数值模拟与试验结果对比Fig.7 Comparison between the compression test by PFC and the experimental results

1.4 模型验证

为验证离散元数值模型的正确性，将自重应力荷载作用下桩心间距为250 mm且路堤高度为300 mm和500 mm 的模型试验结果与PFC 数值模拟结果进行对比分析，如图8 所示.从图中可以看出：离散元数值模拟所得路堤中竖向应力的分布与试验所得的曲线变化趋势相一致，两者间的误差在1.6%～14.0%范围内，说明建立的离散元模型能准确实现对桩承式路堤中土拱效应发展规律的模拟.

图8 PFC数值模拟结果与试验结果对比分析Fig.8 Comparison between the PFC numerical simulations and experimental results

1.5 数值模拟工况

为研究循环荷载作用下桩承式路堤中土拱效应的衰减规律，采用离散元数值模型分析了变化路堤高度、循环荷载振幅σc与加载频率f不同情况下，桩承式路堤中土拱效应的衰减规律，工况如表2所示.

表2 离散元PFC数值模拟工况Tab.2 The programmes of PFC models

2 动载作用下桩承式路堤中土拱效应衰减规律

首先以路堤高度h=500 mm，桩净间距（s-a）=200 mm 为研究对象，分析加载频率f=2 Hz 时，加载50 个循环荷载下路堤中接触力的变化规律；并分析动载振幅σc在5～20 kPa 范围、加载频率f在2～10 Hz范围变化时，桩承式路堤中竖向应力的分布规律；最后通过研究静、动载作用时路堤荷载传递效率的变化，引入土拱效应动力折减系数κ，分析不同加载频率与振幅作用下桩承式路堤中土拱效应的衰减规律，并据此推求土拱效应动力折减系数κ的表达式.

2.1 循环动载作用下土拱效应发展演变过程

图9 为循环动载加载频率为2 Hz 且振幅σc为5 kPa 时一个加载周期过程中路堤中接触力的分布规律.动载采用正弦波荷载形式（如图4 所示），0.00T～0.25T内为动载加载阶段（T为加载周期），0.25T为加载峰值时刻；0.25T～0.75T内为卸载阶段，0.75T为卸载谷值时刻.图9 中接触力的大小按照相同的比例绘制，线条的粗细能够反映出接触力的大小，线条越粗表示接触力越大，称为强力链.

图9 加载-卸载过程中接触力分布变化规律Fig.9 The variation of the contact force at the loading and unloading stages

从图9（a）中可以看出：在靠近桩顶处的接触力线条更加密集且粗，即接触力逐渐向桩上转移并集中，且路堤中的强力链在软土的上方交错形成环形的拱结构，该拱结构对应了土拱的内外拱高度.桩承式路堤中的土拱效应主要是路堤中剪切带的摩擦作用，将本来由软土承担的应力转移至桩或桩帽上，从而减小了软土承担的竖向应力.对比图9（a）和（b）可知，在动载加载阶段（0.00～0.25T），路堤中土拱的外拱高度发生了下降的现象，而内拱的高度基本上没有改变，剪切带的作用区域相应减小，进而减小了传递到桩顶或桩帽上的应力.这说明动载作用下土拱效应作用的范围减小，表明在循环动载加载阶段桩承式路堤中的土拱效应发生了弱化.在卸载阶段（0.25～0.75T），路堤中的接触力在桩上集中的现象越来越不明显，在卸载谷值时刻，路堤中基本观察不到土拱结构的存在，而在下一阶段的加载过程中（0.75～1.00T），土拱结构又逐渐显示出来.这说明在整个循环加载过程中，路堤中的土拱结构始终存在（包括卸载谷值0.75T时刻）.根据路堤表面所作用的循环荷载情况可以看出，在动载加载阶段，土拱结构形态清晰，土拱效应发挥较为明显，路堤中更多荷载传递到了桩上；与加载阶段不同，在卸载阶段特别是卸载谷值的时刻，土拱结构形态不明显，土拱效应发挥不明显.

为进一步分析循环次数对土拱效应发挥的影响，在加载峰值作用下对路堤中接触力的分布规律进行分析，如图10 所示.从图中可知：加载峰值状态下路堤中接触力在桩上集中的现象始终较为显著，但这种接触应力集中的现象随着循环次数NT的增加而逐渐减弱，表现为土拱高度的降低.当循环次数NT≥12T后土拱的高度基本保持稳定，不再发生变化.接触力随着加载周期的变化规律在宏观上将会导致桩土荷载分担比E（定义为桩承担路堤及路堤上所作用荷载的效率）保持较大值，而随着循环加载次数NT的增加，E的值逐渐减小，当NT≥12T时，E的大小保持稳定.

图10 加载峰值状态下路堤中接触应力分布规律Fig.10 The distribution of the contact force along the height of the embankment under the peak load

2.2 循环荷载作用下桩承式路堤中土拱效应动力折减系数的确定

由上文可知，在循环动载的作用下，路堤中的土拱效应会发生衰减弱化.下文将进一步分析不同动载频率f及动载振幅σc对土拱效应发挥的影响.

2.2.1 加载频率对路堤中接触应力分布的影响

图11 为循环动载加载第50 个周期时，振幅σc=5 kPa且加载频率f=2 Hz、5 Hz、10 Hz情况下桩承式路堤中接触力的分布规律.对比图11（a）和（b）可知，在动载作用下土拱结构的外拱高度略有降低，内拱高度基本上没有发生变化，因而土拱效应发生了微小的弱化.随着加载频率的增大［如图11（c）和（d）］，桩承式路堤中土拱结构的外拱高度呈现逐渐减小的趋势，内拱高度也有降低的趋势但并不明显，此时土拱效应作用的区域逐渐减小，土拱效应也逐渐弱化.

图11 加载频率对路堤中接触应力分布的影响Fig.11 The effect of the frequency of the cyclic load on the distribution of the contact force in the embankment

2.2.2 加载振幅对路堤中接触应力分布的影响

图12 为循环动载加载第50个周期时，加载频率f=2 Hz 且动载振幅σc为5～20 kPa 情况下桩承式路堤中接触力的分布规律.可以看出，随着动载振幅σc的逐渐增大，桩承式路堤中土拱结构的内、外拱高度均逐渐降低，土拱效应在这个过程中逐渐发生折减.与变化加载频率时的接触力分布规律相比，动载振幅在增大的过程中，内、外拱高度变化的幅度更明显，表明振幅的变化更能影响桩承式路堤中土拱效应的发挥，下面从桩土荷载分担比的角度进行量化分析.

图12 振幅对路堤中接触应力分布的影响Fig.12 The effect of the amplitude of the cyclic load on the distribution of the contact force in the embankment

2.2.3 土拱效应动力折减系数确定

为定量分析循环荷载的加载频率及动载振幅对桩承式路堤中［1.0≤h/（s-a）≤2.5］土拱效应折减现象的影响，本文分析了土拱效应动力折减系数κ的变化规律，并结合数值模拟结果推求κ的表达式.根据Heitz 等［2］可知κ的定义为静载作用下的桩土荷载分担比Estat与动载作用下的桩土荷载分担比Edynamic间的比值，如公式（1）所示.

公式（1）通过动、静载作用下荷载分担比的比值来反映土拱效应的折减程度.当动载下的桩土荷载分担比Edynamic与静载下的桩土荷载分担比Estat相近，即κ≈1 时，表明土拱效应基本上没有发生折减；当κ＞1时，表明动载作用下土拱效应发生了折减，κ越大，土拱效应的折减程度越明显.

1）土拱效应动力折减系数影响因素分析

图13 集合了静载以及循环动载作用下的桩土荷载分担比的结果，并采用公式（1）计算出了相应的土拱效应动力折减系数κ，其中循环动载的加载频率f在5～10 Hz、加载幅值σc在5～20 kPa 范围变化（见表2）.从图13 中可以看出：路堤的高度与桩净间距的比值h/（s-a）、动载振幅σc以及加载频率f的改变均能影响土拱效应的发挥，但各因素对土拱效应动力折减系数的影响幅度不同.

图13 土拱效应动力折减系数影响因素分析Fig.13 The effect of the variations on the factor of soil arching reduction

从图13 可知：随着h/（s-a）的逐渐增大，土拱效应动力折减系数减小，当h/（s-a）由1.0 增大至2.5 时（增大2.5 倍），土拱效应动力折减系数κ减小了约35%～40%.这主要是由于随着h/（s-a）的增加，土拱效应逐渐完全发挥，土拱的稳定性逐渐增强，此时循环动力荷载对土拱效应的影响逐渐减小，表现为动载作用下的桩土荷载分担比Edynamic与静载作用下的桩土荷载分担比Estat的差异逐渐减小，根据κ的定义并由式（1）可知其值随之逐渐减小.当σc由20 kPa减小至5 kPa（减小75%）时，κ减小了约20%～30%.这主要是由于动载振幅σc的减小削弱了循环荷载对土拱效应的影响，动载作用下的桩土荷载分担比Edynamic与静载作用下的结果差异变小，κ随之减小.而当f由10 Hz 减小至2 Hz（减小80%）时，κ仅减小了约3%～8%.由此可知：h/（s-a）的变化对土拱效应动力折减系数的影响最大.当h/（s-a）取得较大值时［例如h/（s-a）=2.5］，土拱效应动力折减系数维持在1.2～1.6 之间，说明此时桩承式路堤中的土拱结构比较稳定，在循环动载的作用下，土拱效应的折减不明显，这同时表明了路堤的高度与桩净间距的比值h/（s-a）是影响土拱效应稳定发挥的重要因素.而动载频率f对土拱效应动力折减系数的影响不大，动载振幅σc对土拱效应动力折减系数的影响介于h/（s-a）与f之间.因此，在对土拱效应动力折减系数的表达式进行拟合时，需考虑h/（s-a）与σc这两个影响因子.

2）土拱效应动力折减系数表达式的拟合

根据图13 中离散元数值模拟结果，对土拱效应动力折减系数κ的表达式进行拟合.将土拱效应动力折减系数κ按照动载振幅σc的不同分别放在以h/（s-a）为横坐标，κ为纵坐标的图中，如图14 所示.从拟合结果可以发现，当σc在5～20 kPa 变化时，κ随h/（s-a）的变化基本上呈现直线变化的趋势，而4 条拟合曲线的斜率（图14 中虚线所示）相同，并可以用公式（2）统一表示：

图14 不同动载幅值下土拱效应动力折减系数拟合曲线Fig.14 The expression of κ for different amplitude of cyclic loading

式中：b为拟合直线在纵坐标上的截距，由图14 可知b的取值与动载的振幅σc相关.为推求b的表达式，将b放在以σc/（qstat+γh）为横坐标、κ为纵坐标的无量纲图中，如图15 所示.从图中可以看出b随着σc/（qstat+γh）的变化而呈现出直线变化的趋势，b可用公式（3）所示的直线表示：

图15 土拱效应动力折减系数表达式截距的确定Fig.15 The intercept for the expression of the soil arching reduction coefficient

式中：γ为路堤填料的重度.

将公式（3）代入公式（2）中，可以推出土拱效应动力折减系数κ的表达式见公式（4）.

式中：qstat=σm+σc，σm和σc分别为路堤表面上作用的静压力与循环荷载动载幅值.

2.2.4 土拱效应动力折减系数验证

将本文的计算结果与Heitz等［2］开展的动力模型试验结果进行对比，该动力模型试验中桩为正方形布置，根据模型试验缩尺比为1∶3 可以计算出桩心间距s为1.5 m，方形桩帽尺寸a为0.48 m，路堤表面上作用静压力σm为17 kPa.将循环荷载的动载幅值σc=10 kPa与σc=20 kPa情况下的模型试验获得的动力折减系数与由公式（4）计算的动力折减系数进行对比，如图16 所示.本文提出的土拱效应动力折减系数的计算结果与模型试验结果的误差约为1%～35%，由此验证了该表达式的合理性.

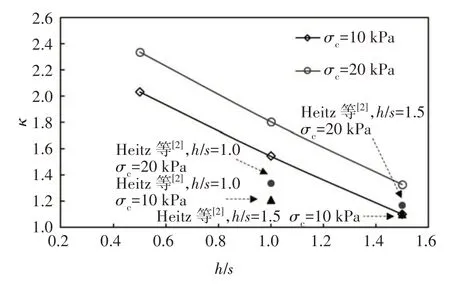
图16 土拱效应动力折减系数验证Fig.16 The validation of stress reduction coefficient of soil arching

3 结论

基于室内模型槽试验建立了桩承式路堤的离散元颗粒流模型，离散元数值模拟结果与自重应力荷载作用下的试验结果误差在1.6%～14.0%范围内，说明建立的离散元模型能准确实现对桩承式路堤中土拱效应发展规律的模拟.在此基础上，采用该模型分析了循环动载作用下桩承式路堤中土拱效应发展演变过程与衰减规律，主要结论如下：

1）研究了完全发挥土拱效应情况［h/（s-a）=2.5］下，循环荷载加载50 次时路堤中接触力的变化规律.结果表明：加载峰值作用情况下，当循环次数NT≥12T后土拱的高度基本保持稳定.

2）路堤的高度与桩净间距的比值h/（s-a）、动载振幅σc以及加载频率f的改变均影响土拱效应的发挥，但h/（s-a）的变化对土拱效应动力折减系数的影响最大，动载振幅σc对土拱效应动力折减系数的影响介于h/（s-a）与f之间.

3）基于离散元数值模拟结果，推求了桩承式路堤中土拱效应动力折减系数κ的表达式，并通过与动力模型试验结果对比分析，验证了土拱效应动力折减系数计算表达式的正确性.