近断层地震下梁式桥考虑SSI 效应的能力谱法

李宇，董世杰，乔云强，赖亚平，薛晓锋

（1.长安大学公路学院，陕西西安 710064；2.林同棪国际工程咨询（中国）有限公司，重庆 401121）

抗震设计的能力谱法是一种计算结构弹塑性地震响应的近似方法，其计算精度虽然低于非线性时程分析法，但它的计算过程比较简洁、计算速率也较高，便于工程人员快速估算结构抗震性能.

能力谱法最初是由Freeman［1］建议的，并为各国规范所采用［2］.目前，已有许多学者对该法进行了改进，例如：Chopra 等［3］建议了改进的能力谱方法，并提出了多模态推覆分析方法；曹一山等［4］提出了适用于桥梁结构的简化能力谱法；王克海等［5］提出了基于模态分析的Pushover 方法；Ahmad 等［6］、陈伟宏等［7］、季春芳等［8］、李延和等［9］都将能力谱法应用于建筑结构的抗震性能评估中；李宇等［10-11］将高阶振型的影响引入能力谱法中，并应用于铁路高桥墩的抗震性能评估中；FEMA440［2］则给出考虑土-结构相互作用（SSI效应）的等效线性化方法，可用于中远场地震下的桥梁抗震设计.

虽然上述学者［1-11］对能力谱法进行了大量的研究，但是还没有文献研究在近断层地震作用下的能力谱法.由于近断层地震可以使建筑物直接承受高能量的冲击，其脉冲性运动也会产生更为严重的震害［12-14］，因此，有必要研究近断层地震作用下的能力谱法.另外，FEMA440［2］所建议的能力谱法虽然能够考虑SSI效应的影响，但它所采用的需求谱是依据国外规范，因此，不能直接应用于我国桥梁的抗震设计中.

综上所述，本文选取了215 条近断层地震动记录，计算了适用于我国桥梁抗震设计的近断层地震弹塑性加速度和位移反应谱，进而得到了考虑近断层地震影响的需求谱，并将其与FEMA440 建议的考虑SSI效应的能力谱法相结合，完善了近断层地震下梁式桥考虑SSI效应的能力谱法.

1 FEMA440考虑SSI效应的方法［2］

在FEMA440中，SSI效应包括［2］：基础柔性效应、运动学效应和地基阻尼效应.基础柔性效应可以在建立结构的有限元模型时，采用模拟基础的转动和平动刚度的弹簧单元来考虑.运动学效应和地基阻尼效应的确定方法阐述如下.

1.1 运动学效应

式中：T为周期，s；e为基础埋深，m；vs为场地剪切波速，m/s；n为剪切波速的折减系数，见表1.

表1 剪切波速的折减系数Tab.1 Reduction factors of shear wave velocity

定义RRS=RRSbsa×RRSe，并分别将弹塑性加速度和位移反应谱的谱值乘RRS，以此来考虑运动学效应对需求谱的影响.

1.2 地基阻尼效应

分别建立结构的固结和柔性基础的模型，并计算得它们的基阶周期分别为T和T′，s

计算固结基础模型的等效单自由度（SDOF）体系的刚度：

式中：M为固结基础模型的总质量（kg）；α1为基阶振型的质量参与系数.

计算基础的平动刚度Kx：

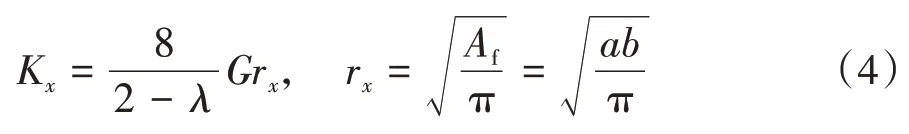
式中：λ和G分别为土的泊松比和等效剪切模量（Pa）；rx为等效半径，m；Af为基础面积，m2。

计算基础的等效转动刚度Kθ和转动半径rθ：

式中：h*为等效计算高度，取结构70%的高度，m.

计算等效周期延长比（/Teff）：

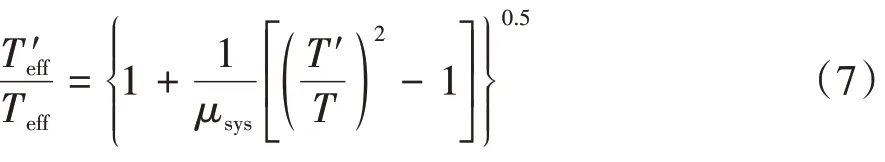
式中：μsys为土-结构系统的预期位移延性比.

计算地基辐射阻尼比βf：

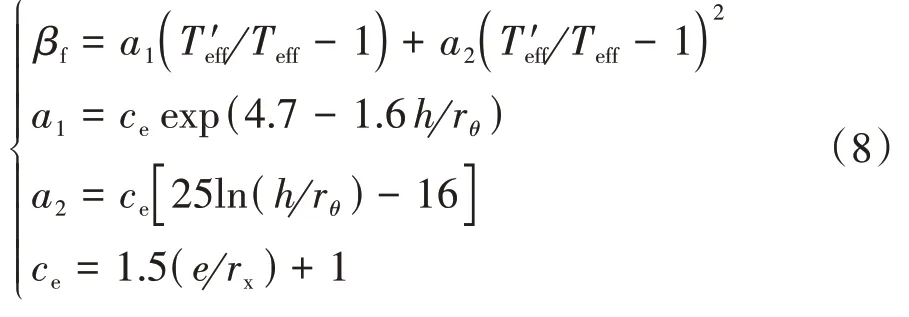
式中：ce、a1和a2都为地基辐射阻尼比的参考系数。

最后，计算土-结构系统的总阻尼比β0：

式中：βi为初始阻尼比，一般取5%.

在此基础上，从用RRS修正后的需求谱（对应不同阻尼比）中，选取与β0对应的需求谱，并与结构的能力谱相结合，以求解结构的性能点.这就考虑了运动学效应和地基阻尼效应的影响.

2 近断层地震的弹塑性反应谱

本节将统计适用于我国桥梁抗震设计的近断层地震弹塑性加速度和位移反应谱，并以此作为本文建议的改进能力谱法的需求谱.

2.1 近断层地震动记录的选取

吕红山等［15］、刘培玄等［16］对我国抗震设计规范［17-18］和美国“NEHRP 报告”［19］的场地类型进行了对比，得到了以下结论（表2）：美国“NEHRP 报告”［19］中v30（土层深度30m 处的剪切波速）＞510 m/s、v30=260～510 m/s、v30=150～260 m/s、v30＜150 m/s 对应的场地类型与我国抗震设计规范［17-18］中I～IV 类场地相对应.

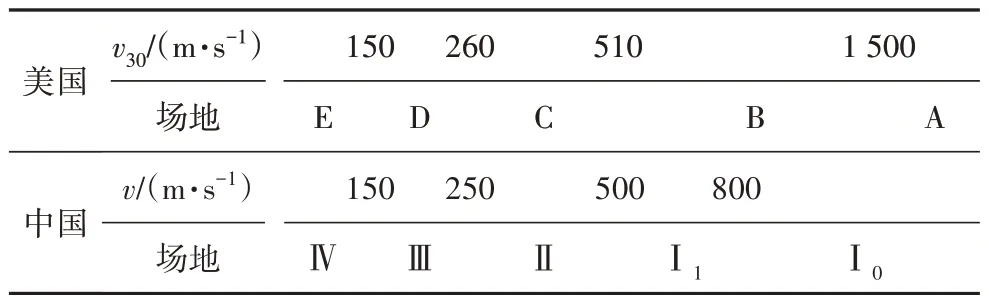
表2 中国和美国的场地分类指标对比Tab.2 Comparison of site classification indicators between Chinese and American codes

另外，根据Liossatou 等［12］、Alici 等［13］、Li 等［14］的研究成果，本文采用的近断层地震动记录的选取原则为：有明显速度脉冲［20-21］，矩震级MR≥5.0，断层投影距离D≤15 km，PGA≥0.05g.

在此基础上，本文从美国的太平洋地震工程研究中心（PEER）的强震数据库中，选取了219 条近断层地震动记录，它们的矩震级MR和震中距R（km）的分布关系见图1.然后，根据中美场地分类指标的对比表（表2），将选取的地震动记录按照我国抗震设计规范的场地类型进行分类，其中：I0类37 条、I1类40条、II类53条、III类45条、IV类44条.

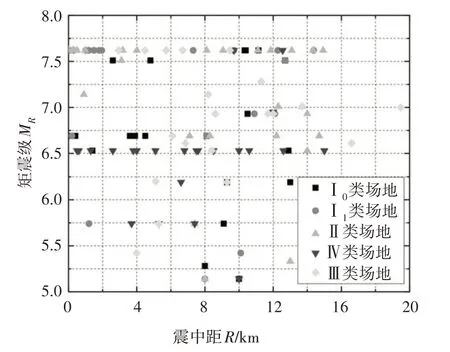
图1 矩震级MR和震中距R的分布关系Fig.1 Relation between MR and R

2.2 近断层地震的弹塑性反应谱

将选取的215 条近断层地震动记录的峰值加速度PGA调幅到0.2g后，输入BISPEC软件中，采用Takeda 刚度退化模型，并取阻尼比ξ=5%、屈服后刚度比η=0.05 和位移延性比μ=1.0～6.0，可计算得对应于ξ=5%和μ=1.0～6.0 的近断层地震弹塑性加速度和位移反应谱，如图2和图3所示.

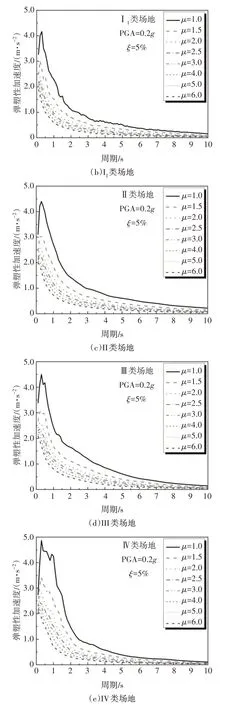
图2 近断层地震弹塑性加速度谱Fig.2 Near-fault elastoplastic acceleration response spectra

2.3 ξ对近断层地震弹塑性反应谱的影响关系式

在考虑地基阻尼效应（1.2 节）后，土-结构系统的总阻尼比会变为β0［式（9）］.因此，在采用能力谱法时，应选取与β0对应的近断层地震弹塑性反应谱，来建立相应的需求谱.图2 和图3 分别为ξ=5%对应的近断层地震弹塑性加速度和位移反应谱，不能直接用于土-结构系统.

图3 近断层地震弹塑性位移谱Fig.3 Near-fault elastoplastic displacement response spectra

为了能够利用图2 和图3（对应ξ=5%）快速求得β0对应的近断层地震弹塑性加速度和位移反应谱，以下将建立ξ=5%和β0分别对应的近断层地震加速度和位移弹塑性反应谱之间的关系.具体做法为：

1）利用2.2 节方法，继续计算ξ=1%、10%、15%、20%对应的Ⅱ～Ⅳ类场地（根据FEMA440［2］，Ⅰ0和Ⅰ1类场地不考虑SSI 效应）的弹塑性反应谱（μ=1.0～6.0）；

2）分别计算ξ=1%、10%、15%、20%与ξ=5%的近断层地震弹塑性反应谱的比值；

3）利用Matlab 拟合ξ对近断层地震弹塑性反应谱的影响系数，即式（10）：

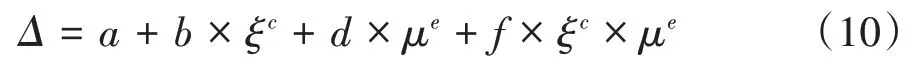
式中：Δ为任意ξ的反应谱与ξ=5%的反应谱的比值；a～f为拟合参数，见表3.

表3 阻尼比对近断层地震弹塑性反应谱的影响系数Tab.3 Impact factor of damping ratio on the near-fault elastoplastic spectra

在此基础上，利用式（10）、图2 和图3，可求得任意ξ的近断层地震弹塑性反应谱.以Ⅱ类场地为例（设μ=3），先由式（9）求得土-结构系统的ξ=8%，再由式（10）算得Δ=0.922 3，并乘图3 的谱值，可得到ξ=8%的弹塑性位移反应谱（图4）.

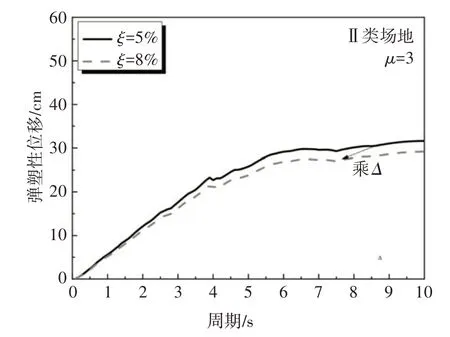
图4 Ⅱ类场地（μ=3）的弹塑性位移反应谱Fig.4 Elastoplastic displacement spectrum of class Ⅱsite（μ=3）

3 近断层地震下考虑SSI效应的能力谱法

本文根据FEMA440［2］考虑SSI 效应的方法（第1节），并采用Chopra［3］的改进能力谱法的步骤，再结合图2、图3、式（10）和表3，完善了近断层地震下适用于我国梁式桥的考虑SSI效应的能力谱法.其详细步骤如下：

1）按照《铁路工程抗震设计规范》（GB 50111—2006）［18］计算基础的水平和转动刚度，并采用弹簧单元来模拟基础，进而建立考虑基础柔性效应的梁式桥有限元模型，并对其进行Pushover 分析，以得到ADRS形式的能力谱；

2）按照梁式桥所处的场地和抗震设防标准，从图2 和图3 中选取对应的近断层地震弹塑性反应谱（ξ=5%），进而绘制近断层地震弹塑性需求谱；

3）由式（1）和式（2）计算折减因子RRS，进而修正第2）步的近断层地震弹塑性需求谱，以此来考虑运动学效应的影响；

4）由式（3）～式（9）计算得土-结构体系的阻尼比β0，并利用式（10）来修正第3）步的近断层地震弹塑性需求谱，以此来考虑地基阻尼效应的影响；

5）将第1）步的能力谱和第4）步的近断层地震需求谱绘制到同一坐标系中，再根据Chopra 等［3］的改进能力谱法的计算步骤，求得等效SDOF体系的性能点，并转化为墩底剪力和墩顶位移.

4 工程实例

4.1 工程简介

某三级公路的梁式桥如图5和图6所示.上部结构为等截面五跨预应力简支箱梁（跨径30 m）；桥墩采用C30 混凝土，截面配置60 根Φ32 的HRB400 纵筋和体积配箍率0.5%的HPB300 箍筋；采用刚性扩大基础（C25 混凝土、边长5 m 的正方形、厚度2 m），基底埋深4 m；处于Ⅱ类场地，8度设防.

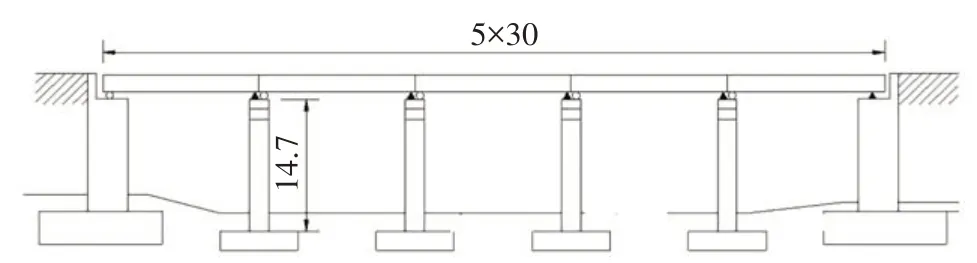
图5 工程实例（单位：m）Fig.5 Project case（unit：m）

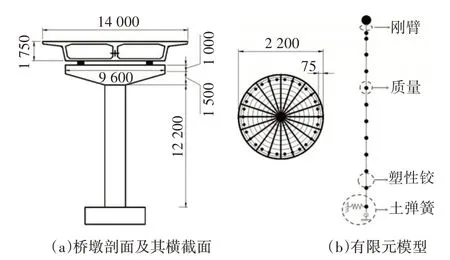
图6 桥墩及其有限元模型（单位：mm）Fig.6 Pier and its finite element model（unit：mm）

4.2 有限元建模

采用SAP2000 软件，按照《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）［17］建立该梁式桥的单墩有限元模型，如图6（b）所示：1）将上部结构质量（5.31×105kg）等效为集中荷载施加于模型顶部，并用刚臂与墩体相连；2）按照《公路桥梁抗震设计规范》（JTG/T 2231-01—2020）［17］计算得墩底塑性铰长度为1.5 m，并用XTRACT 软件计算塑性铰截面的M-φ曲线（图7），以模拟墩底塑性铰；3）根据《铁路工程抗震设计规范》（GB 50111—2006）［18］计算的基础的平动和转动刚度分别为150.85×105kN/m 和56.33×106kN·m/rad，进而在模型底部加设弹簧单元来考虑基础柔性效应.

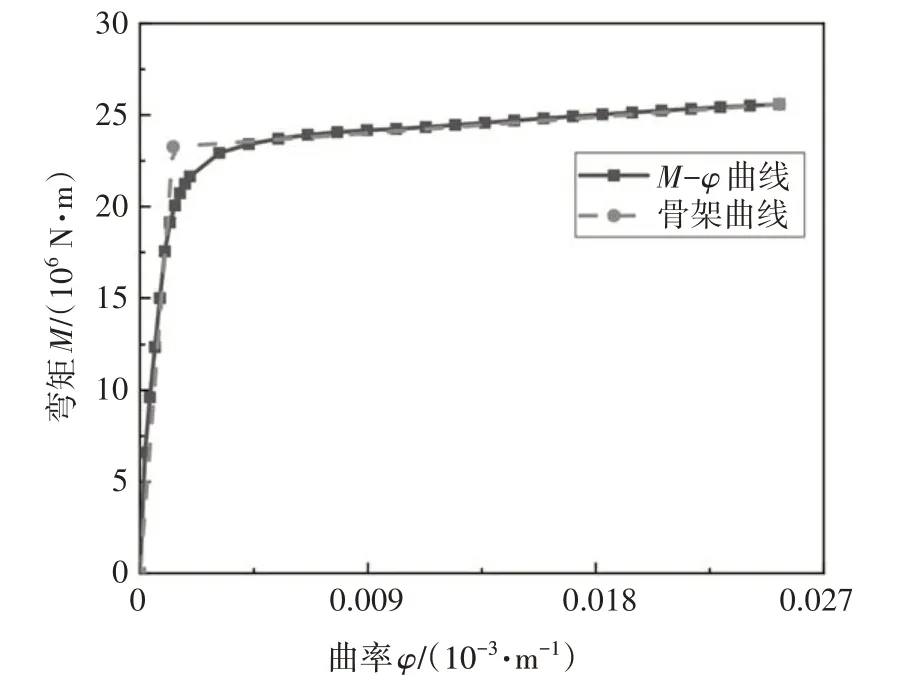
图7 M-φ曲线Fig.7 M-φ curve

4.3 本文改进能力谱法的应用及验证

步骤1计算能力谱曲线（考虑基础柔性效应）

采用SAP2000 软件，对考虑基础柔性效应的有限元模型［图6（b）］进行Pushover 分析，得到了该梁式桥考虑基础柔性效应的能力谱曲线（ADRS形式）.

步骤2计算需求谱曲线（考虑运动学效应和地基阻尼效应）

（1）利用式（1）～（2），可计算得运动学效应的折减因子RRS（图8）.如果将图2 和图3 的近断层地震弹塑性反应谱的谱值乘RRS，即可得到考虑运动学效应的近断层地震弹塑性反应谱.

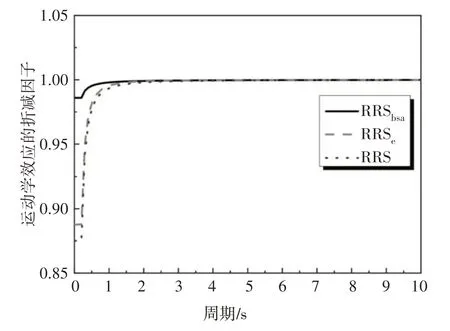
图8 运动学效应的折减因子Fig.8 Reduction factor of kinematic effects

（2）采用SAP2000软件，对有限元模型［图6（b）］进行动力特性分析，可计算得：

①基础固结模型的基阶周期T=0.933 9 s；

②柔性基础模型的基阶周期T′=0.996 5 s；

③基础固结模型的基阶振型的质量参与系数和参与质量分别为α1=0.767 9和m=8.493 9×105kg；

④根据式（3）～式（5）可计算得K*fixed=38 447 kN/m、Kx=2.762 8×106kN/m和Kθ=7.700 6×107kN·m/rad.

在此基础上，对应于不同的μ，可由式（7）计算得等效周期延长比，再由式（8）计算得地基辐射阻尼比βf，最后由式（9）计算得土-结构体系的总阻尼比β0.其中，不同μ对应的/Teff、βf和β0的计算结果如表4所示.

表4 不同μ对应的/Teff、βf和β0Fig.4 /Teff，βf and β0 with different μ

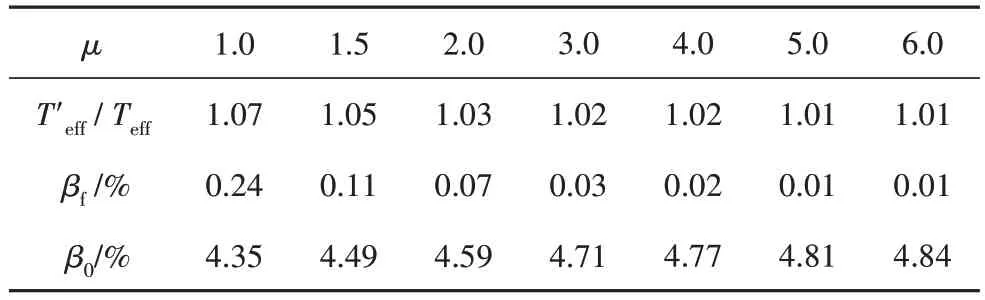
表4 不同μ对应的/Teff、βf和β0Fig.4 /Teff，βf and β0 with different μ

然后，令ξ=β0，并代入式（10）中，即可计算得对应于不同μ的Δ（即得到任意β0的反应谱与图2-3 的ξ=5%的反应谱的比值）.将图2 和图3 的近断层地震弹塑性反应谱的谱值乘以Δ，即可得到考虑地基阻尼效应的近断层地震弹塑性反应谱.

（3）由于该桥处于Ⅱ类场地且为8 度设防，可根据《铁路工程抗震设计规范》（GB 50111—2006）［17］取设计加速度峰值PGAd=0.3g.根据文献［22］的研究成果，可将图2和图3的近断层地震弹塑性反应谱乘αm，以得到与PGAd对应的近断层地震弹塑性反应谱.

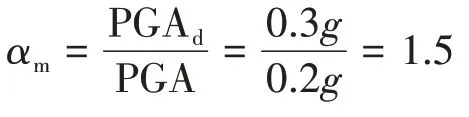
式中：αm为近断层地震弹塑性加速度和位移反应谱的调整系数。

（4）将（1）～（3）计算得到的RRS、Δ和αm乘图2和图3 的近断层地震弹塑性反应谱后，即可得到与PGAd对应的、考虑运动学效应和地基阻尼效应的近断层地震弹塑性反应谱.然后，按照文献［11］的方法，分别以弹塑性加速度为纵坐标（Sa）、弹塑性位移为横坐标（Sd），绘制出与PGAd对应的、考虑运动学效应和地基阻尼效应的近断层地震弹塑性需求谱（图9）.

步骤3将步骤1求得的考虑基础柔性效应的能力谱（图9）与步骤2 求得的考虑运动学效应和地基阻尼效应的需求谱（图9）绘于同一坐标系中，再用Chopra［3］的改进能力谱法来求性能点.具体做法为：

图9 ADRS形式的能力谱和需求谱Fig.9 Capacity and demand spectra with ADRS form

（1）根据图9可求得各交点（a～f）的结构延性，如表5 所示：c（d）点延性大（小）于需求延性.因此，结构的性能点（图9中的星号点）的延性应介于c点和d点之间，并可插值求得其延性为μ=2.727.

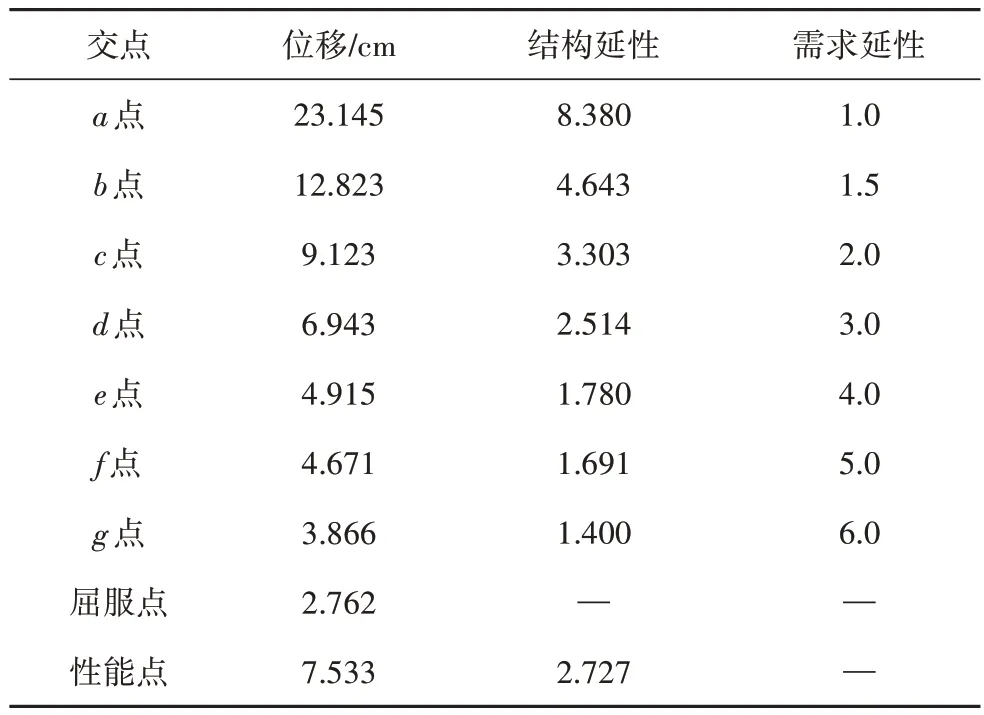
表5 求解性能点Fig.5 Solution of the performance point

（2）在图9 中，进一步查得结构性能点（星号点）的谱位移和谱加速度分别为：Sd=7.533 cm和Sa=2.236 m/s2.然后，根据等效SODF 体系和MDOF 体系的转换关系，按照文献［11］的方法，可计算得墩顶位移和墩底剪力分别为8.152 cm和1 375.85 kN.

步骤4从图1中分别选取Ⅰ、Ⅱ、Ⅲ类场地的近断层地震动记录各7 条，并将它们的PGA 都调幅为0.3g后，输入有限元模型［图6（b）］中，进而用SAP2000 进行非线性时程分析，可算得算例梁式桥的墩顶位移均值和墩底剪力均值，并与本文改进能力谱法和FEMA440 的计算结果相互对比（图10），从中可知：

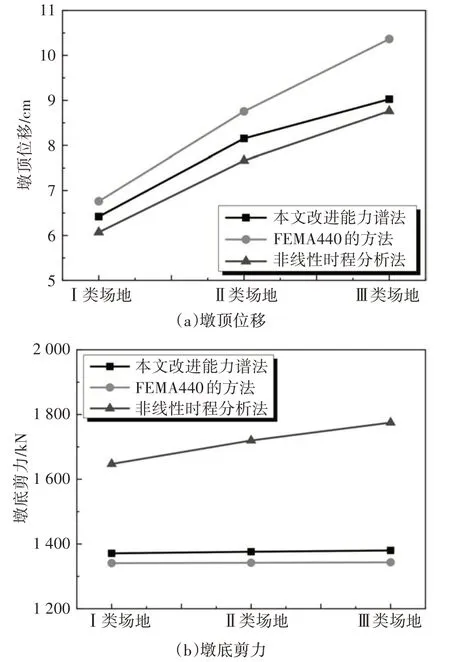
图10 计算结果的对比Fig.10 Comparison of result

（1）与非线性时程分析法计算的墩顶位移相比，本文改进能力谱法和FEMA440 的计算结果的误差分别为8.97%和16.32%.可见，对于近断层地震下考虑SSI 效应的我国梁式桥，FEMA440 的计算结果偏于保守，而本文改进能力谱法是有效且可行的.

（2）与非线性时程分析法计算的墩底剪力相比，本文改进能力谱法和FEMA440 的计算结果都偏小.这是因为能力谱法主要是考虑了结构基阶振型的计算结果，而非线性时程分析法则考虑了结构全部振型的计算结果.

综上所述，本文完善的近断层地震下适用于我国梁式桥考虑土-结构相互作用的能力谱法是有效可行的，可以用于我国梁式桥的抗震性能评估.

5 结论

虽然FEMA440 建议的能力谱法能考虑土-结构相互作用（SSI效应）的影响，但它所采用的需求谱是来自国外规范，即该法不能直接应用于我国桥梁的抗震设计中，而且该法也未能考虑近断层地震动的影响.因此，本文致力于完善近断层地震下我国梁式桥考虑SSI效应的能力谱法，主要工作有：

1）根据近断层地震动特性和我国抗震设计规范，从PEER 强震数据库中合理选取了四类场地的215 条近断层地震动记录.再采用BISPEC 软件计算了适用于我国桥梁抗震设计的近断层地震弹塑性加速度和位移反应谱，并拟合了阻尼比对近断层地震弹塑性反应谱的影响关系式.

2）将计算得到的近断层地震弹塑性反应谱与FEMA440 考虑SSI 效应的方法、Chopra 的改进能力谱法相结合，完善了近断层地震下适用于我国梁式桥且能考虑SSI效应的改进能力谱法，并应用于某梁式桥的抗震性能评估中.

3）与非线性时程分析法的计算结果对比后，可知：对于近断层地震下考虑SSI 效应的我国梁式桥，FEMA440 的计算结果偏于保守，而本文的改进能力谱法是有效且可行的，可以应用于我国梁式桥的抗震性能评估中.