低轨导航星座增强BDS精密单点定位技术验证
2022-10-09邓皓文季海福
邓皓文,孙 迅,蒋 林,季海福
(北京遥测技术研究所,北京 100076)
0 引言
低轨(Low Earth Obirt,LEO)卫星星座能够在全球范围内对北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)提供信息增强和信号增强,将是我国综合定位导航授时(Positioning,Navigation, and Timing,PNT)体系建设的重要组成部分,低轨星座的加入将为卫星导航系统能力的大幅跃升提供有力支撑。精密单点定位(Precise Point Positioning,PPP)是利用国际GNSS服务(International GNSS Service,IGS)组织发布的或用户解算得到的精密卫星轨道与精密卫星钟差产品,综合考虑各项误差模型的精确改正,对单台全球导航卫星系统(Global Navigation Satellite System,GNSS)接收机采集的相位和伪距观测值进行非差定位解算,获得高精度坐标的一种定位方法。非差PPP技术可摆脱大范围、长距离测量对地面参考站的依赖,单机作业灵活,节约用户成本。目前,单系统PPP达到cm级的定位精度需要20min甚至更长的首次初始化时间。
低轨卫星运行速度很快,星座的几何图形结构变化较快,使得定位过程中历元间观测方程的相关性减弱,参数的可估性大大增强,有望从根本上解决载波相位模糊度参数收敛慢的问题,进而缩短PPP收敛时间,实现快速精密定位。斯坦福大学泰勒教授在2016年的ION会议上探讨了低轨星座对全球定位系统(Global Positioning System,GPS)导航的贡献。美国铱星系统与GPS共同研发推出新型卫星授时与定位服务(Satellite Time and Location,STL),已成为GPS的备份或补充,既可以独立地导航、定位,也能对GPS进行信号增强。为了分析低轨导航增强星座对GPS PPP的效果,文献[12]采用无电离层模型结合GPS和LEO卫星进行试验,结果表明,GPS/LEO PPP算法比单独使用GPS的PPP算法收敛时间短,定位精度高。对GPS/LEO PPP和GPS/GLONASS PPP进行了比较分析,在增加相同的可用卫星数量时,GPS/LEO PPP比GPS/GLONASS PPP所需的收敛时间更短,定位精度更高。文献[13]仿真了含有120颗卫星的低轨星座观测数据,评估了LEO星座增强BDS的性能。将LEO数据与BDS-3结合后,卫星能见度和位置精度得到了显著改善,PPP的收敛时间可以从大约30min缩短到1min。文献[14-15]采用仿真观测值评估不同低轨星座增强Multi-GNSS PPP浮点解收敛性能,加入低轨星座后可在数分钟甚至1min内实现收敛。文献[16]探讨了低轨星座增强Multi-GNSS PPP三频固定解的性能。总而言之,GNSS PPP 可利用LEO 卫星几何图形变化快的优势加速定位收敛,有望从根本上解决PPP初始化时间长的难题,真正发挥出PPP技术的优越性。
目前,大多数文献对LEO导航观测数据的仿真方式比较简单且多为数学仿真,但卫星到接收机的几何距离加高斯噪声的方式并不能表示实际的定位情况。本文在上述背景下,构建了BDS/低轨卫星导航增强半实物仿真验证系统,实现了时空基准统一、误差项精细的BDS与低轨星座联合信号仿真与接收,在全星座信号信息模拟与接收测量环境下开展低轨增强BDS PPP技术的试验验证,分析了低轨星座增强BDS PPP的性能。
1 PPP观测模型与数据处理
1.1 联合观测模型
对于低轨增强BDS PPP,采用无电离层模型统一处理BDS与低轨星座的伪距与载波相位观测值。通过形成双频无电离层组合观测值,消除伪距和载波测量中一阶电离层延迟。对于接收机r观测到的卫星s,其伪距与载波相位组合观测值的方程如下

(1)
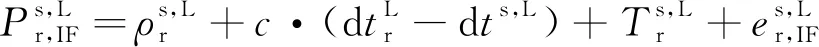
(2)

(3)
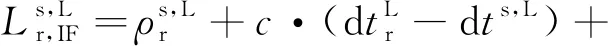
(4)
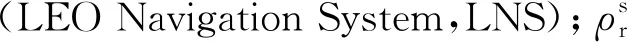
1.2 数据处理与参数估计
低轨增强BDS PPP算法数据处理流程主要包括:数据预处理、精密星历和卫星时钟内插、误差改正以及滤波解算。数据处理流程如图1所示。导航终端除接收常规的GNSS导航信号与广播星历外,同时接收低轨卫星导航信号与广播星历以及低轨卫星、GNSS卫星的精密轨道与钟差数据。在获取联合观测数据以及增强信息后,首先进行数据预处理与发射时刻卫星星历和时钟内插。在此基础上进行各项误差改正。对系统误差源进行模型化改正,模型化卫星天线和接收机天线相位中心偏移、相对论效应、相位缠绕误差、地球自转、固体潮、海潮、极潮等系统误差源,并对卫星坐标、接收机坐标或者观测值进行改正。

图1 低轨增强PPP数据处理流程Fig.1 LEO enhance precise point positioning technology flow
观测模型中的对流层延迟干分量使用模型改正,天顶湿分量延迟作为待估参数进行估计,并使用全球投影函数(Global Mapping Function, GMF)将天顶对流层延迟投影到斜向路径上。
=·
(5)
式中,为斜向对流层湿分量延迟;为对流层湿分量投影函数;为天顶对流层湿分量延迟。
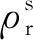
=+d·Δ+d·Δ+d·Δ
(6)
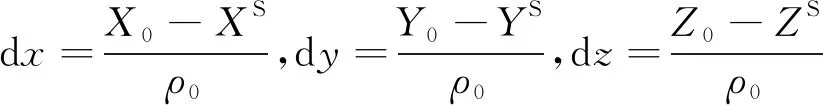
(7)
式中,为卫星到接收机的近似几何距离;Δ,Δ,Δ为坐标增量;,,为接收机近似坐标。
对无电离层组合进行系统误差改正、天顶对流层延迟投影到斜向方向和几何距离线性展开后,将观测方程采用矩阵形式表示为式(8)。若某一时刻共观测到个卫星,状态向量的表达式如式(9),其对应的系数矩阵为式(10)。观测量是扣除近似距离和系统误差改正数的无电离层伪距和载波相位。
2=2×(+5)·+5-2
(8)

(9)
=
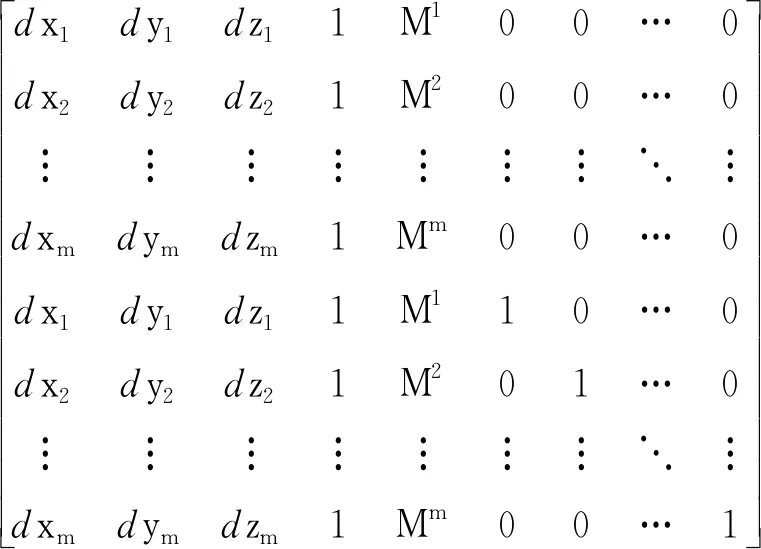
(10)
采用扩展卡尔曼滤波(Extended Kalman Filter,EKF)算法对参数进行估计,待估参数包括接收机坐标增量、接收机钟差、天顶对流层湿延迟和载波相位模糊度。分析验后残差进行质量控制。具体的数据处理策略如表1所示。
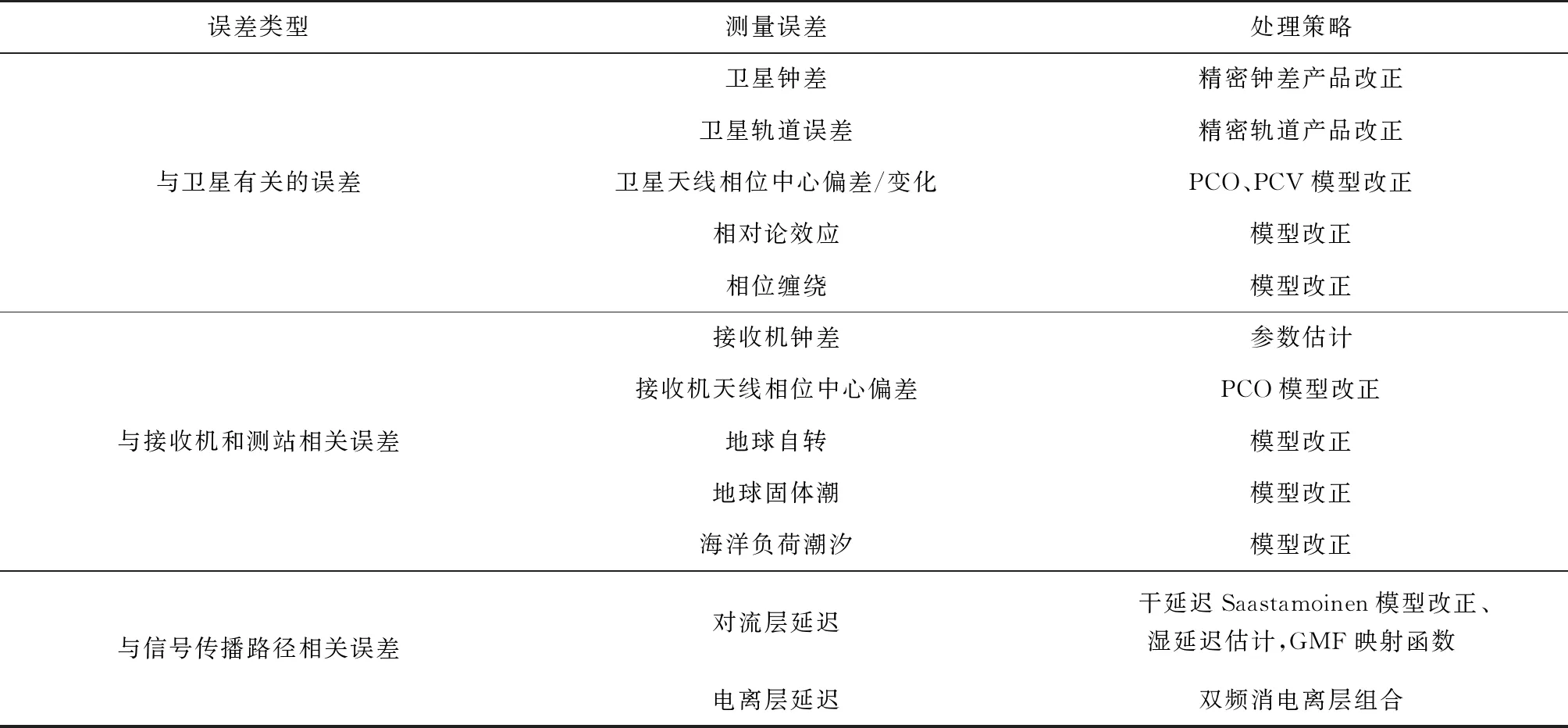
表1 误差模型及处理策略
2 低轨导航增强半实物仿真验证系统
观测值的数学仿真是在测站及卫星的几何距离上加入各模型误差项以及噪声,以模拟观测数据。低轨卫星轨道低,所受到的大气阻力、地球非球形引力和广义相对论作用均明显高于中高轨。此外,卫星轨道低导致卫星运动速度快,轨道周期短,决定了在进行星座仿真时,为保证仿真数据精度,星历拟合周期、数据插值间隔等方面的要求高于中高轨卫星系统。本文选用更精细的力模型参数和处理策略,将低轨卫星星历参数增加至20个,广播星历预报15min星历参数截断误差损失在mm量级。通过数学仿真给出的观测数据精确地生成射频信号,以模拟真实卫星信号,从而进行全链路物理信号验证。
如图2所示,低轨导航增强仿真验证系统由低轨导航增强模拟器和低轨导航增强终端组成,可实现BDS与大规模低轨导航卫星群的实时精密信号模拟仿真,以及时空基准统一的轨道、钟差、空间环境传输及误差仿真模拟,提供全星座信号信息及误差,模拟与仿真接收测量环境,支持组合精密定位算法和关键技术的试验仿真以及技术指标的测试验证。

图2 低轨导航增强仿真验证系统Fig.2 LEO navigation augmentation simulation evaluation system
2.1 低轨导航增强模拟器
低轨导航增强模拟器进行的组合仿真分为BDS星座仿真模块和低轨导航增强星座仿真模块。BDS星座仿真模块仿真BDS全星座(3GEO+3IGSO+24MEO)。低轨导航增强星座仿真模块的低轨星座采用120颗倾斜轨道星座+30颗极轨星座结合的混合星座。倾斜轨道星座构型为Walker 120/12/0,轨道高度975km,轨道倾角55°;极轨星座进动速度与Walker星座进动速度一致,可实现全球任何地点任何时刻最低10°仰角的至少二重以上覆盖。
输入星历初始文件、载体轨迹、仿真时刻、闰秒等信息后,数学仿真模块根据得到的初始轨道及仿真工程的具体设置和轨道积分,生成整个工程所需要时间段的卫星轨道,产生星历、历书等导航参数;根据载体接收机和卫星位置生成卫星到接收机的几何距离,考虑地球自转、对流层延迟、电离层延迟、相对论效应等各项误差改正,生成卫星到接收机的伪距、伪距速度、伪距加速度、伪距加加速度供模拟信号源使用。模拟信号源使用数学仿真给出的观测数据精确生成射频信号。
除了实现低轨卫星轨道仿真、星历和历书信息仿真以及低轨卫星误差和观测值计算外,低轨导航增强仿真模块还进行了增强信息仿真,生成卫星轨道改正数、卫星钟差改正数、格网电离层改正数等信息,时间基准统一到北斗时。半实物仿真系统的仿真误差配置如表2所示,测试场景如图3所示。
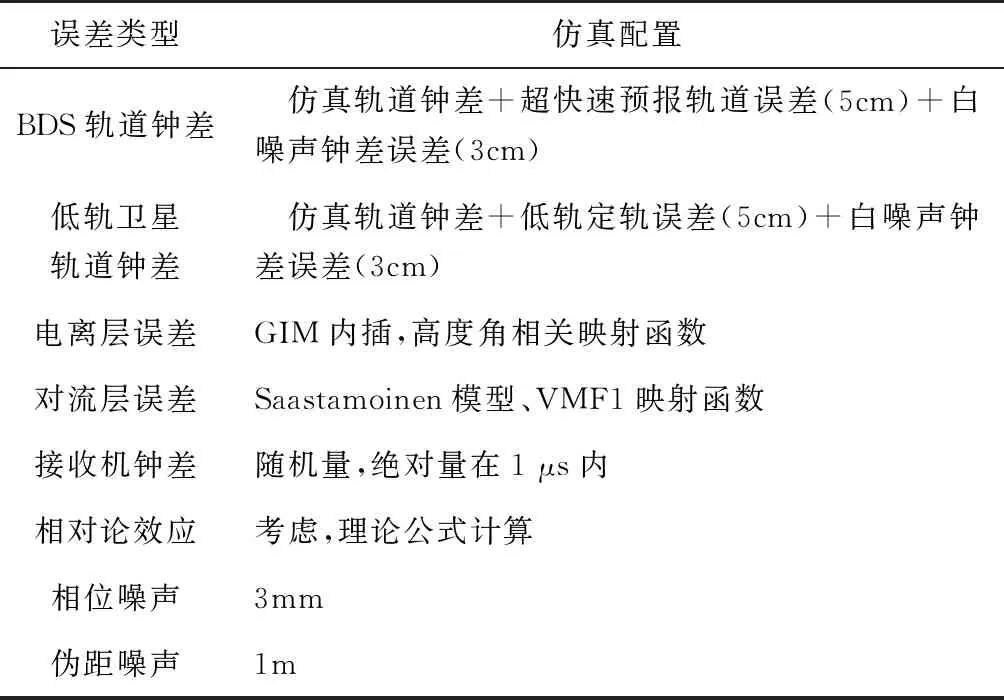
表2 半实物仿真误差配置
2.2 导航增强终端
导航终端一方面接收BDS及低轨星座的导航信号、广播星历,另一方面接收低轨星座播发的BDS及低轨增强信息,建立联合观测模型,基于增强信息对观测值进行误差修正(精密轨道、钟差产品,模型修正),并利用低轨信号的快速变化特性,实现载波相位快速收敛,完成低轨增强的近实时PPP解算。

图3 半实物仿真测试场景Fig. 3 Hardware-in-the-loop simulation testing scenarios
3 低轨增强BDS PPP试验与结果分析
利用上述搭建的低轨导航增强验证平台进行了BDS/LNS联合定位观测仿真。选取20个MGEX测站仿真了2021年6月3日的BDS与低轨双系统伪距和载波相位观测数据,将snx周解坐标设为测站真实坐标,模拟的测站分布如图4所示。BDS观测数据频点为B1、B3,采样率为1s。利用BDS及低轨双星座观测数据分别进行单BDS和低轨增强BDS静态PPP试验。将PPP解算结果与测站真实坐标进行对比,做差获得E、N、U这3个方向上的坐标偏差,当3个方向上的定位偏差均小于10cm时,认定为定位收敛。
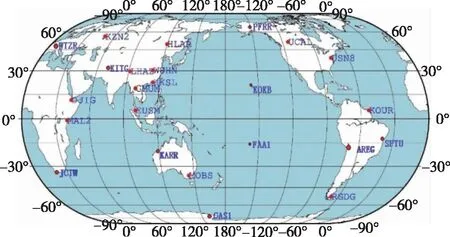
图4 全球测试站分布Fig.4 Global monitoring station layout
3.1 定位收敛时间
对20个测站的BDS单独PPP以及BDS+LNS组合PPP结果进行统计,图5所示为AREG站初始1h的定位结果偏差序列。从图5(a)可以看出,单BDS星座PPP达到收敛需要24min,而低轨增强BDS PPP 达到收敛所需时间较短,只需要75s。从图5(b)可以看出,定位收敛过程中存在收敛跳变,此过程对应的可见星数如图6所示。此时新加入了1颗低轨卫星,说明新加入的低轨卫星观测值可有效加快定位收敛。
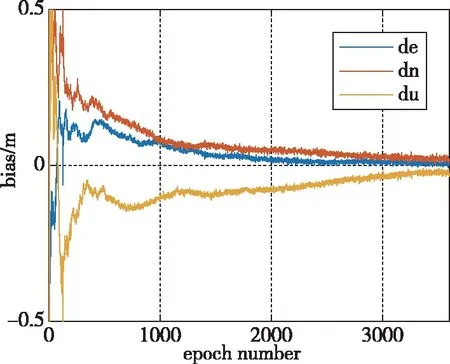
(a) BDS

(b) BDS+LNS图5 AREG站BDS、BDS+LNS PPP定位偏差序列Fig.5 Position bias of BDS, BDS+LNS PPP at station AREG
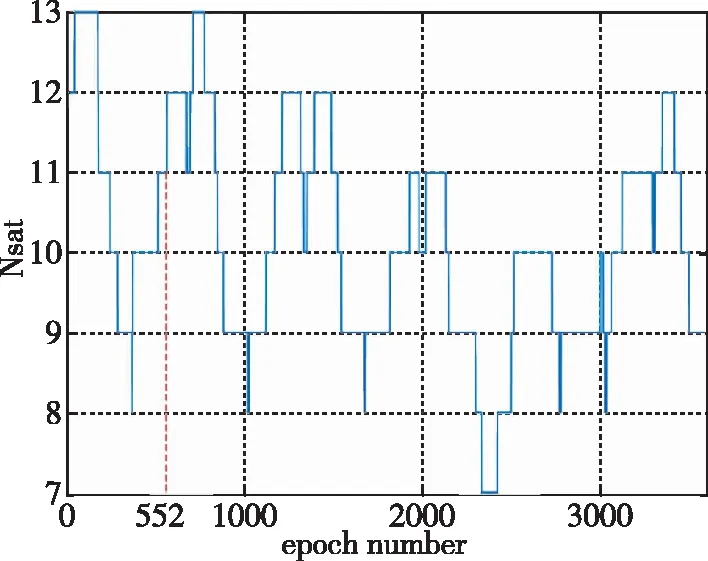
图6 AREG站BDS、BDS+LNS PPP 可见卫星数Fig.6 Satellites number of BDS, BDS+LNS PPP at station AREG
20个测站的BDS PPP以及BDS+LNS PPP收敛时间统计结果如图7所示。可以看出,单BDS星座进行PPP解算时,定位精度收敛到10cm以内大概需要十几分钟,这一点与实际情况相类似;而加入低轨导航卫星的观测值之后,定位精度收敛到10cm之内只需要1min,模糊度的收敛速度加快。图8所示为该时段BDS、BDS+LNS的位置精度因子(Position Dilution of Precision, PDOP)值。可以看出,加入低轨卫星后,20个测站的卫星几何分布均有提升。在采用3GEO+3IGSO+24MEO的BDS全星座构型下,20个测站的 PDOP值在1.9左右;加入低轨导航星座之后,20个测站的PDOP值降为1.5左右。

图7 BDS、 BDS+LNS组合收敛时间(单位:秒)Fig.7 BDS, BDS+LNS convergence time(units : s)

图8 低轨星座加入后的PDOP改善情况Fig.8 BDS/BDS+LNS PDOP
3.2 定位精度
在PPP解算模糊度收敛之后,截取1h的定位结果,计算E、N、U这3个方向上的坐标偏差RMS,分析加入低轨导航星座之后对PPP精度的影响。3个方向的定位精度如图9所示,20个测站单BDS定位精度水平方向整体优于5cm、高程方向整体优于8cm。单BDS PPP东方向均值为2.6cm,北方向均值为1.4cm,高程方向均值为3.4cm;加入低轨星座后,低轨增强BDS PPP东方向均值为1.5cm,北方向均值为0.3cm,高程方向均值为2.2cm。20个监测站收敛后组合定位较BDS-3单独精密定位,定位精度从5cm左右提升到3cm左右;各方向定位精度均有提高,东方向定位精度提升42.3%,北方向定位精度提升78.6%,高程方向定位精度提升35.3%。
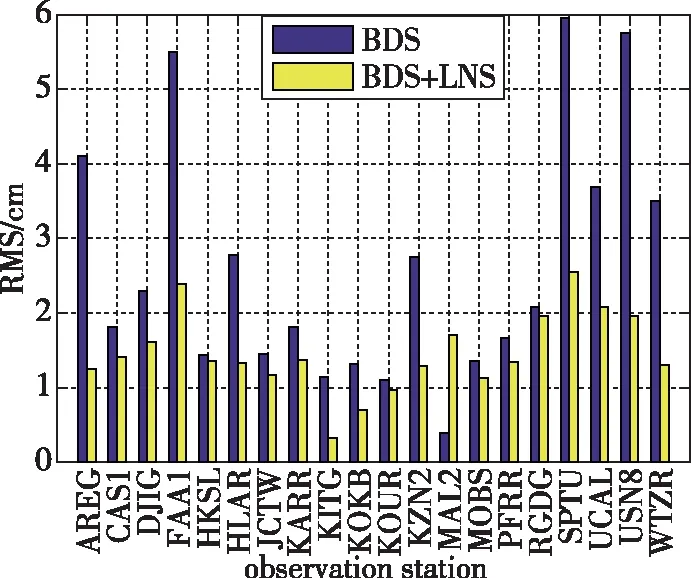
(a) 东方向定位精度

(b) 北方向定位精度
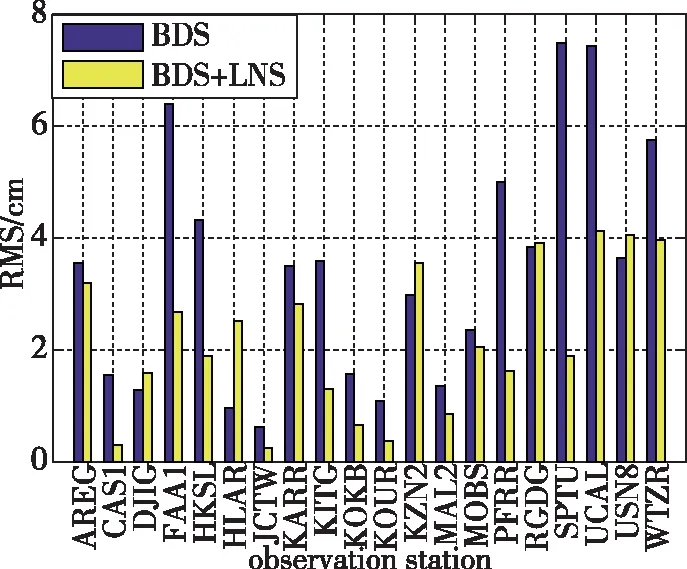
(c) 天方向定位精度图9 BDS+低轨星座组合精密定位精度改善情况Fig.9 BDS +LEO constellation precise position accuracy
4 结论
本文实现了低轨导航星座增强BDS PPP算法,并利用搭建的低轨导航增强半实物验证平台仿真双系统观测量,进行了单BDS及低轨增强BDS PPP试验,评估了低轨增强BDS PPP的定位性能。结果表明:1)20个测站BDS静态PPP收敛时间平均为13min,加入低轨卫星观测值之后,PPP精度收敛到10cm之内只需要1min,说明新加入的低轨导航星座对PPP收敛速度有很大提升,给PPP技术的实时应用提供了可能;2)截取收敛后1h的定位结果,收敛后的组合定位精度可提升至3cm,各方向定位精度均有提高,低轨卫星观测值可提高PPP精度;3)研制的低轨导航增强仿真验证系统可实现时空基准统一的BDS及低轨信号仿真,提供全星座信号信息及误差,模拟与仿真接收测量环境,支持精密定位算法和关键技术的全链路闭环试验以及技术指标的测试验证。
