无人飞行器集群仅测距初始相对位姿确定方法研究

2022-10-09龚柏春管叙军郝明瑞

导航定位与授时 2022年5期

丁鑫，龚柏春，管叙军，郝明瑞

(1. 南京航空航天大学航天学院，南京 210016；2.复杂系统控制与智能协同技术重点实验室，北京 100074)

0 引言

当前，无人飞行器通过集群协同的方式执行任务的应用越来越广泛，例如协同侦察、森林火灾探测及危险环境中执行搜救等。相较于单个高价值、多载荷的无人飞行器，集群无人飞行器具有雷达截面小、成本低、数量多、容错率高等特点，能够通过群体协同效应实现单个大型飞行器难以完成或者代价太大的任务。

实现集群成员间的高精度相对定位是保障集群任务的关键前提。传统的集群飞行器常使用独立于集群外的、提供公共参考坐标的外部定位系统实现成员间相对定位，如运动捕捉系统(Motion Capture System，MCS)和全球导航卫星系统(Global Navigation Sa-tellite System，GNSS)。但MCS需要预先布置于环境中，无法应用于未知环境，GNSS导航信号在复杂环境中存在衰减、多路径效应、无信号甚至信号欺骗等问题。因此，GNSS拒止环境下无人飞行器集群的自主相对导航已经成为行业内的热点问题。

M.Kriegleder等研究了基于无人飞行器的仅测角机载红外传感系统，由于红外传感器视野范围有限，需要在不同方向布置机载传感器阵列，以实现目标飞行器始终处于测量视野范围内。也有学者研究了基于视觉相机的相对定位系统，但基于视觉的定位系统需要测量飞行器对目标飞行器进行追踪机动，以保证目标处于观测视野内，且当目标飞行器距离较远时，视觉相机存在特征识别点模糊等问题，一定程度上限制了无人飞行器间的相对飞行距离。

机载无线电设备能够实现全方位通信测距，且相邻设备间的通信几乎不受空间环境的影响，近年来受到了领域内研究人员的广泛关注。通过在环境中布置多个超宽带(Ultra-Wideband，UWB)固定锚点，可以实现对无人飞行器的测距定位。也有学者研究了基于机载蓝牙传感器，无固定测距锚点的相对定位算法，该算法需要集群成员交换地理北及速度信息。Guo K.等利用单架悬停的无人飞行器作为UWB通信测距锚点，实现集群成员间的相对定位，这种方法仍然需要地理北及速度信息，且集群成员的初始定位需要单架无人飞行器悬停才能启动。S.Helm等研究了一种基于蓝牙通信测距，并使用光流法测速辅助的相对定位算法，但光流法测速只适用于低速飞行和光线良好的任务场景，因此该方法对飞行速度及环境条件均有一定限制。F.M.Martel等研究了UWB测距和视觉即时定位与地图构建(Simultaneous Localization and Mapping，SLAM)组合的相对定位算法，该算法通过最少6次通信测距求解2台设备的4自由度相对位姿，视觉SLAM装置用于测量每台设备相对于各自位置原点的位移，但其同样只适用于低速环境，且对机载计算资源有较高要求。T.M.Nguyen等通过在无人飞行器及追踪目标上分别安装2个UWB天线，同时使用光流法测速，实现了无人飞行器对移动目标的相对定位，但受限于双天线的安装距离，只能实现较近距离的相对定位。

因此，为了解决上述问题，实现GNSS拒止环境下无人飞行器集群成员间的自主相对导航，本文研究了一种基于机载惯性测量单元(Inertial Measurement Unit，IMU)、气压高度计与数据链测距组合的相对位姿求解算法。在建立飞行器三维运动的水平坐标系投影等效模型的基础上，求解状态量相对位置及航向角的线性最小二乘问题。通过引入递推最小二乘算法(Recursive Least Squares，RLS)，实现了相对位姿估计的实时输出，并给出了使系统状态量不可观测的几种飞行形式。仿真结果表明，该算法能够有效降低机载计算负载，并快速稳定地求解无人飞行器间的初始相对位姿。

下面首先建立二维坐标系下的相对位姿求解算法，然后引入该算法的递推求解形式，再对所提算法的可观测性进行理论分析，最后进行数值仿真实验和结果分析。

1 仅测距初始相对位姿确定算法

1.1 运动解耦与水平坐标系定义

无人飞行器在空间坐标系下相对惯性系包含位置及姿态信息，其中姿态角由俯仰角、滚转角及偏航角组成。当其携带气压高度计时，高度方向的位置信息可直接获得，此时可以将各无人飞行器的空间位置及姿态投影至与其固连的当地水平坐标系{}下，该坐标系原点位于质心，轴指向天，和轴位于水平面内，轴指向飞行器的线速度方向，轴方向由右手法则确定。轴与地理北的夹角定义为航向角，偏西向为正。此时{}系的等效偏航角速率为

(1)

令无人飞行器本体系下的加速度为，{}系的加速度为，则有如下关系式成立

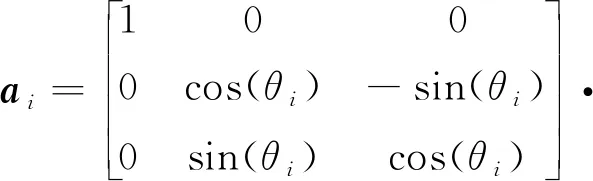
(2)

在水平面内的投影为′，则有

′=

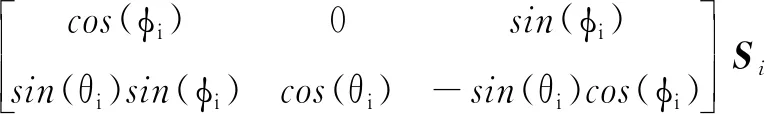
(3)

此时，无人飞行器在空间中的运动已解耦为：角速度为、加速度为′的二维平面运动和高度方向的竖直运动，因而可将三维空间下无人飞行器的相对姿态求解问题简化为二维平面下的相对航向角及相对位置求解问题。

令无人飞行器间的空间距离为，高度差为Δ，则无人飞行器在二维平面下的距离可通过式(4)求出

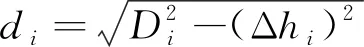
(4)

其中，由机载通信数据链通过TOA(Time of Arrival)模式测量得到；Δ由2个飞行器的机载气压高度计测量的高度作差得到。

图1 坐标系定义与测距示意图Fig.1 Coordinate system definition and UAV ranging diagram

表1 向量表示

1.2 建立相对定位算法

利用文献[16]中的方法，2个飞行器测距时满足如下方程

(5)

且和满足如下表达式

=cosΔ-sinΔ+

(6)

=sinΔ+cosΔ+

(7)

将式(6)和式(7)代入式(5)后，整理可得

=-2-2+(-2-2)cosΔ+

(2-2)sinΔ+2+2+

(8)

其中

(9)

(10)

当2个飞行器进行次通信测距时，则可获得个如式(8)所示的方程，将由这个方程构成的方程组整理成如下矩阵形式

×7=×1

(11)

式中，为包含相对位置及航向角的待求解未知量；×7为系数矩阵；×1为包含测量信息的列向量。、×7和×1的具体表示如下

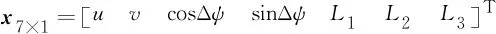
(12)

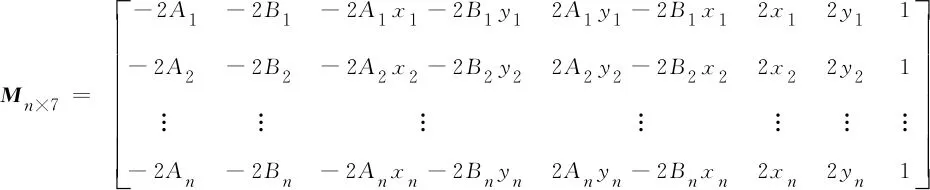
(13)

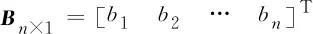
(14)

由式(13)和式(14)可知，矩阵×7和×1中的元素均为已知量，将式(11)中×1移至等号左边，并构造新的矩阵×8=[-]，因此式(11)可进一步表示为

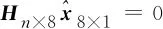
(15)

式中

[cosΔsinΔ1]

(16)

当=5时，rank()=5，由秩-零化度定理可知，矩阵的核空间为3，因此式(15)矩阵方程的解可表示为矩阵的极大线性无关组,,的线性组合

(17)

式中，、为待求解系数。

(18)

(19)

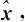
当≥6时，利用最小二乘算法(Least Squares，LS)，可直接求得式(11)中未知量的近似解

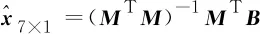
(20)

利用上述方法最少利用5次航向角、加速度信息和测距数据,即可求解2个飞行器间的相对位置和航向角的估计值。

2 RLS

从理论上讲，仅利用5次通信测距和对应时刻的加速度测量信息就可以求解出初始相对位姿，但由于数据链测距存在随机误差，IMU的陀螺仪和加速度计测量值也有常值误差和随机误差，那么利用矩阵中5行7列元素间的约束关系进行位姿解算会存在较大误差，求解得到的极大线性无关组,,波动较大，最终导致算法求解结果误差波动较大。而利用多次通信测距数据构建LS(式(11)中≥7)，可以避免求解矩阵的极大线性无关组，同时利用多次测量数据逼近未知量的真值，降低了单次测量数据对算法求解影响的权重。同时，为了尽可能节省飞行器机载运算资源，这里采用递推算法进行相对位姿的实时求解及输出。

当有≥7次测量数据时，式(11)中的矩阵及列向量×1可以表示为

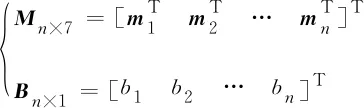
(21)

式中，为矩阵的第行数据，且是维数为1×7的行向量。

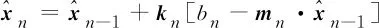
(22)

其中，是修正增益，是维数为7×1的列向量。具体地，仅测距初始位姿确定的RLS计算公式如下

(23)

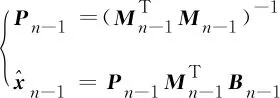
(24)

式中，估计初值由前20次通信测距生成，即生成估计初值时=21。选取前20次测量数据生成初值的原因将在数值仿真4.2.1节中进行详细说明，当达到总测距次数时，递推算法结束运行。

RLS利用时刻的测量数据对-1时刻的状态估计值进行修正，进而得到时刻的状态估计值。具体地，递推过程中每次测量生成的数据列和及递推算法的运算流程分别如图2及图3所示。

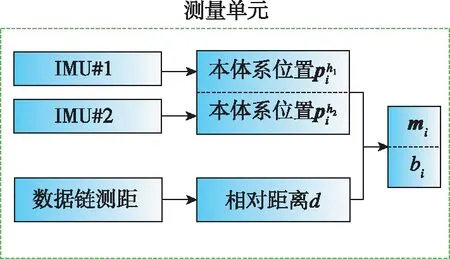
图2 测量数据列流程图Fig.2 Flow chart of measurement column

图3 递推算法流程图Fig.3 Flow chart of RLS algorithm

3 状态可观测性分析

理论上讲，如果通过单次或多次的测量值作为输入，能够确定出唯一的系统状态量(物理可行解)，那么这个系统就是可观测的。与完备测量系统不同，本文研究的欠测量系统的状态可观测性是变化的，会受到相对运动的约束，因此有必要对系统进行状态可观测性分析，给出使系统状态不可观测的相对运动形式，用于指导飞行实践。下面就根据上文中提出的拟合求解方法对系统状态可观测性进行分析。

当测距次数为5次时，将矩阵方程式(11)生成的矩阵展开

(25)

若rank()=5，则矩阵方程式(15)可以求得唯一解。因此，只要使的秩小于5，算法就无法求解出未知量的真值。使rank()<5直观的方法有：2个飞行器中的其中1个绝对静止(如图4所示)；2个飞行器均沿直线飞行(如图5所示)。

图4 算法求解结果发散形位1Fig.4 Algorithm-diverging position 1

图5 算法求解结果发散形位2Fig.5 Algorithm-diverging position 2

当测距次数大于5次时，使用RLS辨识式(11)中未知量的值。由于矩阵的每一列数据分别代表待辨识参数对应分量的观测值，因此当矩阵的某一列观测值为0时，该分量的观测值始终不存在，也就无法求解得到该分量的最小二乘辨识，或者求解值趋于无穷大。观察式(13)中矩阵的元素组成可知，当观测飞行器B沿直线飞行时，=0(其在本体系下的轴分量为0)；当观测飞行器B静止时，和均为0(和轴分量均为0)。同理，当被观测飞行器A沿直线飞行时，=0；当被观测飞行器A静止时，和均为0。

为了得到飞行器A相对于飞行器B的位置及航向角，只需辨识待求解未知量的[cosΔsinΔ]分量，而以上分量分别对应于矩阵的前四列，只要这几列的观测值不为0，就可通过LS辨识出其对应的真值。由前面的分析可知，当2个飞行器以如下描述的轨迹飞行时，飞行器B无法辨识出飞行器A的相对位置及航向角：

1)飞行器B沿直线飞行，且飞行器A沿直线飞行或静止；

2)飞行器B静止，而飞行器A做任意机动。

值得注意的是，由前面的分析可知，当飞行器B做S形机动时，飞行器A无论沿直线飞行或是静止不动，飞行器B均可估计出飞行器A的相对位置，但飞行器A静止时，飞行器B则无法估计出相对航向角。

4 数值仿真

4.1 仿真轨迹与参数设置

假设飞行器A在二维水平惯性系下的初始位置为[0，100]，飞行器B初始位置为[0，0]，2个飞行器以小于5m/s的相对速度飞行，总飞行时长为60s。为了验证可观测性分析的结论，这里生成了两类飞行轨迹：图6所示为使系统状态可观测的飞行轨迹，2个飞行器分别以不同角速度做匀速S形机动；图7(a)和图7(b)所示为第3节状态可观测分析中指出的1)和2)两种使系统状态不可观测情况对应的典型飞行轨迹。图7(a)展示了2个飞行器均沿直线匀速飞行时的轨迹，图7(b)展示了飞行器A做匀速S形机动，飞行器B静止不动时的飞行轨迹。

图6 状态可观测轨迹Fig.6 Observable state trajectory

(a) 2个飞行器均沿直线飞行的轨迹

(b)飞行器B静止，而飞行器A做S形机动的轨迹图7 状态不可观测轨迹Fig.7 Unobservable state trajectory

采用的机载IMU由陀螺仪和加速度计组成，假设二者的测量误差主要包括常值误差和随机误差；数据链测距误差只包含随机误差，将该误差建模为零均值高斯白噪声。这些传感器的误差参数如表2所示。

表2 机载测量仪器误差

4.2 算法求解结果

4.2.1 状态可观测轨迹求解结果

采用4.1节图6生成的系统可观测轨迹进行飞行器间初始相对位置及航向角的递推求解。飞行器测距时间间隔为1s，采用飞行0～20s(20次测距)的数据进行初值生成，而不是5次测距。选取该测距次数的主要原因在于：在采样间隔较小时，飞行器在各自初始坐标系下的相对运动不明显，采样点连线近似直线，即飞行器的飞行形式接近图5给出的使求解算法失真的飞行形位，初始估计偏差较大。

图8和图9分别展示了使用RLS进行1000次打靶仿真求得的B飞行器对A飞行器的初始位置估计误差及其分布。初始航向角估计误差的分布如图10所示。

图8 X和Y轴位置估计误差Fig.8 X- and Y-axis position error

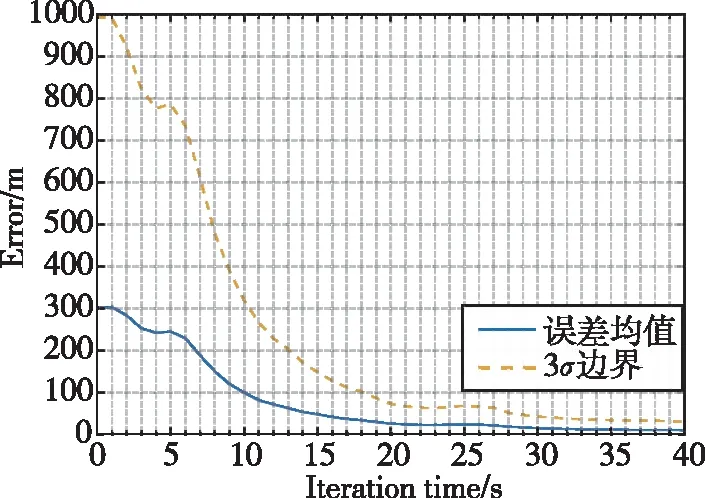
图9 距离估计误差Fig.9 Distance estimation error

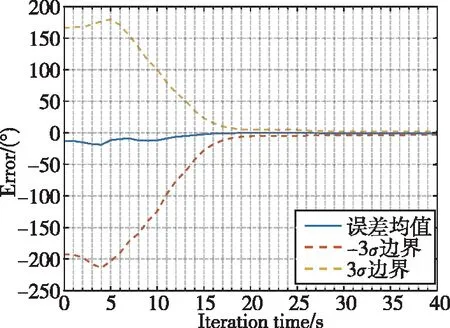
图10 航向角误差估计Fig.10 Heading angle estimation error

由图8及图9可知，运用RLS生成的位置估计初值误差及标准差较大，表明初值估计波动大，可信度较低。迭代运算的前20s(测距20次)，初始位置估计及标准差迅速收敛。迭代至40s时，位置估计误差趋于稳定，且误差均值约为9m，达到初始相对距离的10%以内。由图10可知，航向角初始估计误差均值较小，但标准差较大，表明其估计误差波动较大，估计值可信度较低。迭代运算的前20s，标准差下降明显，估计误差迅速收敛。当迭代运算至40s时，估计误差趋于稳定，且误差均值在1°以内。

4.2.2 状态不可观测轨迹求解结果

由第3章状态可观测性理论分析可知，在图7(a)和图7(b)两种飞行轨迹下，飞行器B无法估计出飞行器A的相对位置及航向角。图11和图12分别展示了在这两种飞行轨迹下飞行器B对飞行器A的相对位置和航向角估计误差及其分布。

(a) X和Y轴位置估计误差

(b) 航向角误差估计图11 2个飞行器均沿直线飞行时，飞行器B对飞行器A的相对位置及航向角估计误差Fig.11 The relative position and heading angle estimation error of UAV B relative to UAV A when both UAVs are flying in straight lines

(a) X和Y轴位置估计误差

(b) 航向角误差估计图12 飞行器B静止，而飞行器A做S形机动时，飞行器B对飞行器A的相对位置及航向角估计误差Fig.12 The relative position and heading angle estimation error of UAV B relative to UAV A when UAV B stands still and UAV A flies a S trajectory

由图11和图12的仿真结果可知，迭代至40s时，两种飞行轨迹下的相对位置单轴估计误差均值均大于1000m，且相对航向角估计误差均方差均大于100°。因此，飞行器B无法估计出飞行器A的相对位置和航向角，即仿真结果验证了理论分析中状态不可观测的飞行轨迹。

为了进一步说明无人飞行器的飞行轨迹对递推算法可观测性的影响，下面将通过表格的形式对2个飞行器在不同轨迹组合下，飞行器B对飞行器A的相对位置及航向角的估计结果进行仿真总结，仿真结果如表3所示。

表3 飞行轨迹和仿真结果

表3中，“√”表示飞行器B在该飞行轨迹下可以估计出飞行器A的相对位置轴分量、轴分量或航向角Δ的值，“×”表示无法估计出对应的值。

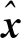
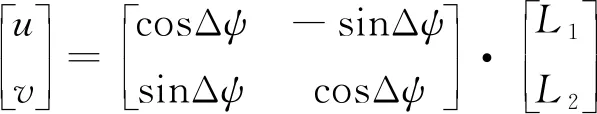
(26)

因此,可以认为这种情况下飞行器B仍然对飞行器A的轴位置分量具有观测性。

由表3可以看出，当飞行器B做S形机动时，其对飞行器A的相对位姿状态量有较高的可观测性；当飞行器B沿直线飞行时，其对飞行器A相对位姿状态量的可观测性开始降低；当飞行器B完全静止时，其完全失去了对飞行器A状态量的可观测性。因此，表3的仿真结果验证了第3节的可观测性分析结论，并为算法的飞行实践提供了有意义的指导。

4.3 算法求解速率分析

本节对5次测距算法、LS以及RLS的求解效率进行对比分析，算法程序的运算环境为6核Inter Core i5-10400处理器。以4.1节使系统状态可观测的无人飞行器轨迹(图6)为例，测距时间间隔为1s，分别对以上三种相对位姿求解算法进行了1000次打靶仿真，获得各算法对应的平均求解时间及相对位置求解精度,如表4所示。表4中，相对位置求解误差指和轴求解误差的平方和开根，即距离误差。算法运行时间越短，位置误差均值及方差越小，则认为求解效率越高。对于5次测距算法，当总测距数据大于5次，如30次测距时，按照总测距次数等间隔取样5次进行位姿解算。

表4 算法求解效率

由表4可以得出以下结论：

1)从算法求解时间来看，5次测距算法耗时最长，算法运算量最大，这是因为在测量数据较少的情况下，对测量数据的进一步解算(如生成矩阵的极大线性无关组、线性无关组的系数解算)需要较多运算步骤。直接对线性方程组求取最小二乘逆的算法(LS)求解时间最短，与其在求解结果方面等价的RLS次之，且递推算法随着测距次数的增多，单次递推求解时间不变，总运算时间线性增长。

2)从算法求解误差来看，当测距次数为30次时，5次测距算法求解的位置误差均值及方差最小，LS及RLS算法位置求解误差及方差相当。当测距次数大于30且不断增大时，LS及RLS算法的位置误差及方差均快速下降，且均小于5次测距算法对应的求解误差。

综上可知，在测距次数较少时，5次测距算法能够利用测距数据间的关系解算得到比LS及RLS精度更高的结果，但需要付出比其他两种算法更多的时间代价，且该算法只利用了5次测量信息，因此误差波动极大。RLS能够在每次递推过程中输出当前的相对位姿估计，且每次计算只消耗极小的机载算力，相较于在进行一段飞行时间后消耗较多机载算力才能给出相同估计精度的LS，以及误差波动较大的5次测距算法，RLS在计算的实时性及稳定性方面具有显著优势。

4.4 算法敏感性分析

运用RLS求解2个无人飞行器初始相对位置的误差源主要包括：飞行器间测距误差，由机载IMU常值漂移引起的本体系下的位置误差。由于该递推算法在解算过程中同时存在位置误差及测距误差，无法反映单个误差因素对算法精度带来的影响。图13展示了当飞行器位置信息准确时，测距误差对姿态解算精度的影响。图14展示了飞行器测距无误差，但其中1个飞行器本体系下的位置测量存在误差时，对姿态解算精度的影响。

图13 航向角及位置估计误差关于测距噪声均方差的曲线Fig.13 Heading angle and position mean absolute errors(MAE) as functions of distance measurement noise standard deviation

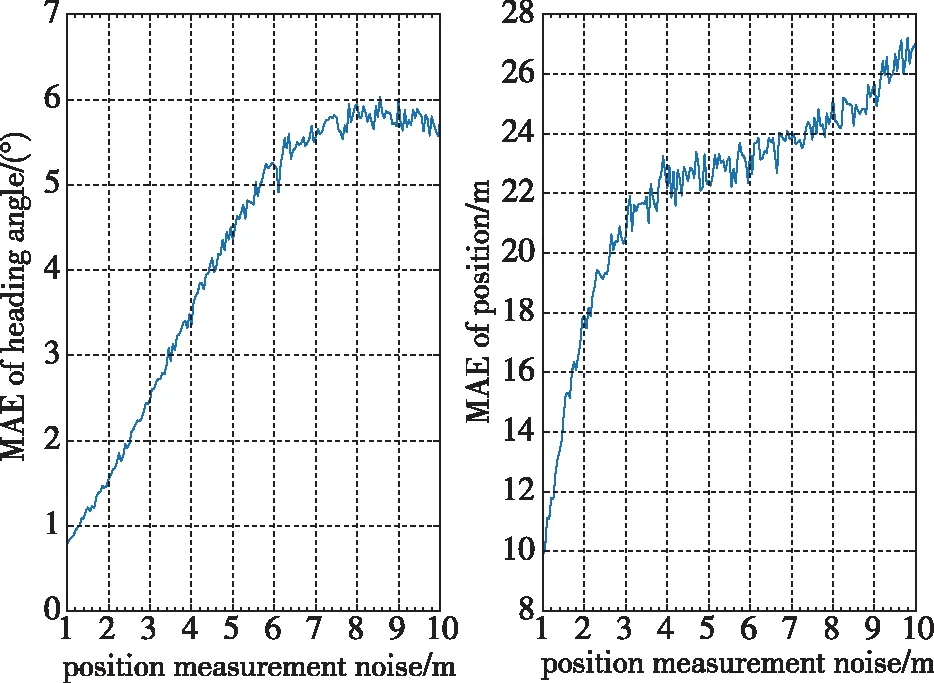
图14 航向角及位置估计误差关于位置测量噪声的曲线Fig.14 Heading angle and position mean absolute errors(MAE) as functions of position measurement noise standard deviation

由图13可知，航向角及位置估计误差与测距噪声近似成正比关系。观察式(8)可以发现，只有项包含距离测量量，因此当测距误差逐渐增大，而其他系数项均不变时，各项对应的未知量求解误差均匀增大。

从图14可以看出，航向角估计误差及位置估计误差随位置测量噪声的增大均呈现增大趋势，且估计误差的增大趋势逐渐放缓。比较图13及图14可以发现，估计算法对测距敏感度远大于位置测量敏感度。这可以由式(8)说明，此时当其中1个飞行器位置测量存在误差时，式(8)左侧误差增大，右侧前三项未知量系数误差同样增大，一定程度上减小了误差对未知量的影响。