基于组合模型高精度预测弹丸径向速度的方法

田 珂

(中国人民解放军63861部队,吉林 白城 137001)

靶场试验中利用连续波雷达准确测试弹丸的炮口初速,主要通过将雷达测试的径向速度转换为切向速度后递推得出。径向速度是指在雷达与弹丸的方向上,雷达测试弹丸的飞行速度,切向速度是指弹丸在飞行轨迹的切向上的速度,而弹丸初速是指弹丸在飞出炮口瞬间的切向速度,因此弹丸炮口初速通过将雷达测试的一定时间内的径向速度近似转换为对应时间的切向速度后再拟合递推得到。但是当遇到雷达死机、天气条件不良、火炮发射故障或者弹丸自身异常时,雷达捕获的径向速度会出现缺失,导致计算出的炮口初速不准确。预测缺失的径向速度成为解决这一问题的重要手段。目前研究弹丸径向速度的文献很多,文献[1]主要研究如何实时高精度对弹丸径向速度进行处理,前提是雷达能够完整捕获到弹丸的径向速度,并未考虑到弹丸径向速度缺失时的解决办法;文献[2]提出了在弹丸径向速度缺失时,利用回归模型预测出缺失的数据,主要研究的是大口径弹丸,并未提到小口径弹丸的解决办法,而且没有考虑到单项模型预测精度不理想的情况;文献[3]研究的是根据径向速度检测低速目标的问题,前提依然是获取到部分径向速度,当径向速度不完整时该方法将无能为力。由于雷达测试的径向速度属于一维数据,而ARIMA(autoregressive integrated moving average,ARIMA)模型、GM(grey model,GM)(1,1)灰色模型和回归模型(model of regression)都是针对一维数据建模的,正好可以用这3种模型建模预测。由于大口径弹丸自身质量较大,初速高,重力、风的阻力等各种因素对其速度的影响较小,所以大口径弹丸的径向速度的下降变化量基本不变,单调线性变化特征较为明显;小口径弹丸自身质量较小,初速小,重力、风的阻力等各种因素对其速度的影响较大,径向速度下降变化量始终在变化,导致其既具有线性变化特征又具有非线性变化特征。ARIMA模型擅长预测出数据中的线性特征,预测非线性特征的能力较弱,GM(1,1)模型擅长预测出数据中的线性特征,预测精度较高,但无法预测出非线性特征,回归模型中的一元线性回归模型能预测出线性特征,二次多项式回归模型能预测出非线性特征,但两者有时预测精度会不理想,而且单一模型的预测能力有限,只能预测出径向速度中的部分特征。因此,为尽可能提高预测精度,在按照迭代方式预测的前提下,选择利用ARIMA模型、GM(1,1)灰色模型与一元线性回归模型共同建立线性组合模型,预测出大口径弹丸缺失的径向速度;利用ARIMA模型、GM(1,1)灰色模型与二次多项式回归模型共同建立非线性组合模型预测出小口径弹丸缺失的径向速度,这样就把所有模型的预测优势整合到一起。实验发现,组合模型的预测精度高于所有单项模型,整体预测误差和单项预测误差,均小于1‰,更加适合作为弹丸径向速度预测模型。

1 单项模型建模原理

1.1 ARIMA模型建模原理

ARIMA模型于1976年提出,在许多领域都得到了广泛应用,研究实践也证实了它的有效性。ARIMA模型是自回归模型的差分形式与移动平均模型相结合的结果,即同时包含了自回归和移动平均成分,模型表达式为

=-1+-2+…+-+--1--2-…--

(1)

式中:表示当时刻处于时,的取值是其前期序列值的多元线性回归,受过去期序列值的影响;为随机干扰,属于误差项;表示当时刻处于时,的取值是其前期的随机扰动的多元线性函数,受过去期随机扰动的影响,即是时刻之前期序列值、误差项和期随机扰动共同作用的结果。

ARIMA模型通常可以表达为ARIMA(,,),其中为差分阶次。要对径向速度建立ARIMA模型,首先要采用ADF(augmented dickey-fuller,ADF)单位根检验法准确检验平稳性。如果径向速度对应的检验统计量中对应的概率值远远小于临界统计值0.05,说明该数据序列是平稳序列,否则是非平稳的,此时需要对其进行差分处理,直到变为平稳序列为止;然后利用LB(Ljung-Box)检验法检验时间序列是否为白噪声序列,如果检验统计量对应的概率值远小于0.05,说明径向速度对应的数据序列是非白噪声序列,此时就可以直接进行建模,如果是白噪声序列,说明径向速度中没有可被提取的有用信息,则无法建模。ARIMA模型能够解决非平稳时间序列预测的建模问题,只有将数据序列转换为平稳非白噪声序列才能建立ARIMA模型,即利用数据序列中稳定的信息预测后期的数据,所以该模型无法预测出潜藏的随机因素,同时该模型的优点是预测短期数据精度较高,而预测长期数据误差会很大。通常采用自相关图和偏自相关图显示的特征确定模型中的参数,,。模型类别确定好以后,还要检查模型残差是否是白噪声序列。如果模型残差LB检验统计量对应的概率值远大于0.05,说明模型残差是白噪声序列,意味着有用信息已经提取完毕,所建模型通过了检验,可以直接利用所建模型进行后期预测;如果模型残差LB检验统计量对应的概率值远小于或等于0.05,说明其是非白噪声序列,表示有用信息尚未提取完毕,需要重新确定模型类别,直到模型残差变为白噪声序列为止。

1.2 GM(1,1)灰色模型建模原理

(2)

式中:=1,2,…,。GM(1,1)灰色模型的算法是先对数据序列进行累加然后再进行累减。检验GM(1,1)灰色模型预测结果用后验差比值和小误差概率进行评价,如表1所示。灰色模型同样擅长预测出数据序列中的稳定信息,擅长进行短期预测,且精度较高,但对随机因素预测会出现误差较大的情况,而且进行长期预测精度并不理想。

表1 GM(1,1)预测结果评价表

1.3 回归模型建模原理

回归分析的目的是了解两个或多个变量间是否相关、相关方向及强度,并建立数学模型以便通过观察特定变量来预测或控制相关变量的方法。线性回归模型在处理线性变化的原始数据方面预测精度很高。一元线性回归模型是分析因变量与自变量之间的线性关系,数据模型为

(3)

式中:和为回归系数。

多项式回归模型的数学表达式如式(4)所示,因变量和自变量是次多项式关系。

=+++…++

(4)

检验回归模型的过程:方程的显著性检验主要根据检验统计量对应的概率值与临界统计值005进行比较来判断,如果远小于0.05,就说明回归模型是显著的,否则不显著;模型的拟合效果是根据参数Multiple R-squared和Adjusted R-squared与1的比较结果进行判断,如果它们取值都非常接近1,就说明模型的拟合效果很好;回归系数是根据其检验统计量对应的概率值与0.001的比较进行判断,如果远小于0.001说明回归系数是显著的,否则说明回归系数不显著。回归模型拟合线性特征和二次曲线特征的能力较强,但是模型较为简单,对相关特征的拟合精度还有待提高。

2 组合模型建模原理及方法

组合预测模型是利用相同的样本信息从不同的分析角度对未来信息进行预测,它把所属预测模型的预测结果进行总体性综合考虑,最大限度利用所有预测模型的样本信息,这样考虑问题更全面、更系统,深化对时间序列演化规律的认识。

(5)

在组合模型中关键是求解权系数,具体思想是:对单一模型误差平方和较小的模型赋予较高的权系数,对单一模型误差平方和较大的模型赋予较小的权系数,进而使组合模型误差平方和尽可能小,权系数的确定方式为

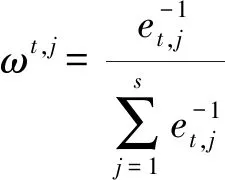
(6)

式中:,为第期第个单项模型预测值与实测值的误差平方和。由式(5)或式(6)可知,先计算出第期单项模型的误差平方和就可以计算出第期单项模型的权系数,最后就可以计算出组合模型的预测值。

3 组合模型应用及分析

实验选择利用RStudio软件环境进行数据分析、统计建模及数据可视化。为了验证ARIMA模型、GM(1,1)灰色模型与回归模型新建立的组合模型的预测精度高于所有单项模型,选择采用4组径向速度实测数据进行验证。针对大口径弹丸而言,从0.1 s开始每隔0.005 s选取一发径向速度值,一直取到0.5 s为止,共获取到81发径向速度值。而针对小口径弹丸而言,从0.05 s开始每隔0.005 s选取一发径向速度值,一直取到0.3 s为止,共获取到51发径向速度值。4组径向速度数据分别记为DATA1、DATA2、DATA3和DATA4,其中DATA1和DATA2是大口径弹丸的径向速度数据,DATA3和DATA4是小口径弹丸的径向速度数据,其时间序列曲线分别如图1～图4所示。针对DATA1和DATA2而言,把第1～71发径向速度作为训练数据,训练ARIMA模型、GM(1,1)灰色模型和回归模型,把第72～81发径向速度作为测试数据,检验这3个模型及其组合模型的预测精度的高低。具体原理:先利用第1～71发数据训练3个模型,预测出第72发数据后,利用组合模型原理计算出第72发数据的组合模型预测值,再把第72发实测值代入到训练数据中,预测出第73发数据,以此类推就可以得到DATA1和DATA2中第72～81发径向速度3个模型及其组合模型的预测值。针对DATA3和DATA4而言,把第1～41发作为训练数据训练3个模型,第42～51发作为测试数据,检验3个模型及其组合模型的预测精度的高低。先利用第1～41发数据训练3个模型,然后预测出第42发径向速度,利用组合模型建模原理计算出第42发组合模型预测值,然后把第42发实测值代入到训练数据中,再预测出第43发数据,以此类推,就可以得到DATA3和DATA4第42～51发径向速度3个模型及其组合模型预测值。先以DATA1为例进行验证分析。

图1 DATA1时间序列图

图2 DATA2时间序列图

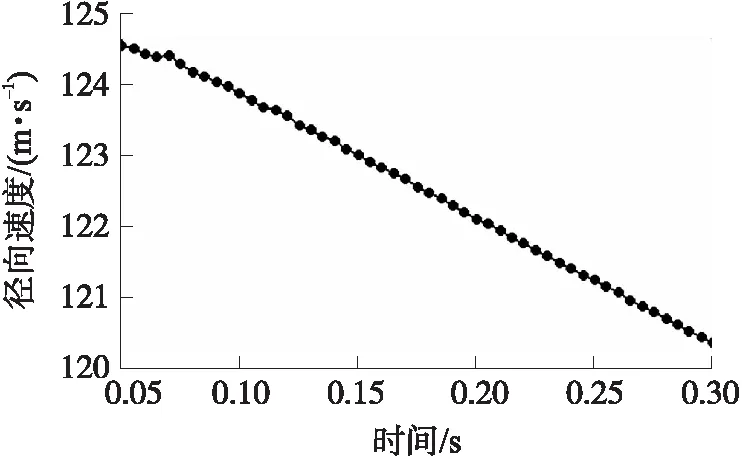
图3 DATA3时间序列图

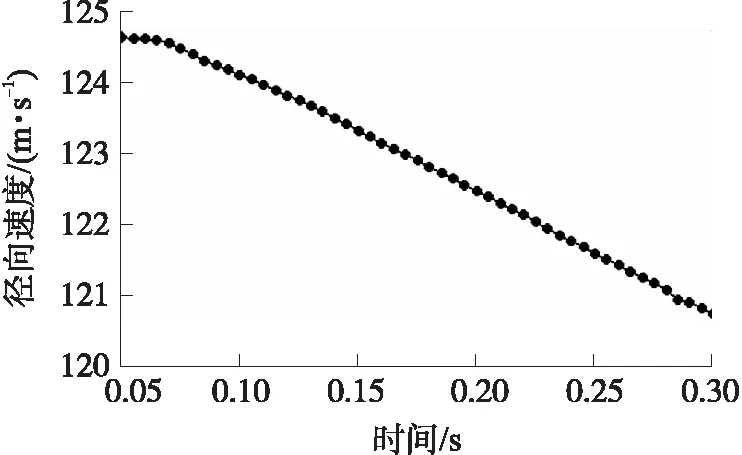
图4 DATA4时间序列图

3.1 ARIMA模型建模预测

DATA1第1～71发数据的ADF单位根检验统计量对应的概率值为0.01,小于临界统计值0.05,LB检验统计量对应的概率值为2.22×10,远远小于临界统计值0.05,说明DATA1第1～71发数据是平稳非白噪声时间序列。DATA1第1～71发数据对应的自相关图显示出拖尾的特点,如图5所示;偏自相关图是一阶结尾,如图6所示,再结合BIC信息图可以确定模型类别为ARIMA(1,0,0)。模型残差的LB检验统计量对应的概率值为0.495 8,远大于临界统计值0.05,所以模型残差为白噪声序列,即数据中的有用信息已经提取完毕,模型通过了检验,可以进行预测,最后得到DATA1第72发数据的ARIMA模型预测值。采用同样的方法最后可得到DATA1第72～81发ARIMA模型预测值。

图5 DATA1第1～71发数据自相关图

图6 DATA1第1～71发数据偏自相关图

3.2 GM(1,1)模型建模预测

经过检验发现DATA1第1～71发数据的级比都处于区间[0.972 604 5,1.028 167]之中,满足建立GM(1,1)灰色预测模型的条件,经过建模预测得到DATA1第72发GM(1,1)模型预测值,预测结果显示后验差比值=0.007 959 138,预测精度=99.973 13%,预测精度等级为“好”。采用同样的方法最后得到了DATA1第72～81发GM(1,1)模型预测值。

3.3 回归模型建模预测

由于DATA1属于大口径弹丸的径向速度,整体呈线性分布,所以对DATA1第1～71发数据建立速度与时间的一元线性回归模型,模型拟合结果显示检验统计量对应的概率值小于2.2×10,远小于临界统计值0.05,说明回归模型是显著的;Multiple R-squared为0.999 5,Adjusted R-squared为0.999 5,两者取值都非常接近1,说明模型的拟合效果很好;截距估计值检验对应的概率值小于2×10,回归系数检验对应的概率值小于2×10,两者都远远小于0.001,说明截距估计值和回归系数都是显著的,最终证明可以用所建一元线性回归模型进行预测,再把第72发径向速度对应的时间数据代入到所建模型中就可以预测出第72发径向速度。采用同样的方法总共就可以得到DATA1第72～81发径向速度一元线性回归模型预测值。而DATA3和DATA4属于小口径弹丸的径向速度,其径向速度时间曲线属于二次曲线,应该建立速度与时间的一元二次多项式回归模型。实际上,以DATA3为例,经过检验发现:建立径向速度与时间的一阶线性回归模型时,Multiple R-squared为0.986 0,Adjusted R-squared为0.985 9;建立径向速度与时间的二次多项式回归模型时,Multiple R-squared为0.994 0,Adjusted R-squared为0.993 7。两个模型的其余检验结果均符合要求,对比得出DATA3更适合建立径向速度与时间的二次多项式回归模型。

经过3个模型对DATA1的建模预测,最后就得到了3个模型及其组合模型预测出的DATA1第72～81发径向速度,实测值与预测值如表2所示,绘制其时间序列关系曲线,如图7所示。经过计算得到ARIMA模型预测值与DATA1第72～81发实测值的平均相对误差为0.136%,GM(1,1)灰色模型预测值与实测值的平均相对误差为0.06%,一元线性回归模型预测值与实测值的平均相对误差为0.159%,组合模型预测值与实测值的平均相对误差为0.042%,小于1‰的误差标准,而且组合模型每发预测值与实测值的相对误差的关系曲线如图8所示,每发预测值与实测值的相对误差均小于1‰,所以组合模型整体的预测精度和单项预测精度均达到了雷达测试弹丸径向速度的误差要求。

表2 DATA1第72～81发实测值与各模型预测值

图7 DATA1第72～81发实测值与各模型预测值关系曲线

图8 DATA1组合模型预测值与实测值相对误差变化曲线

采用对DATA1建模预测的方法应用于DATA2,就可以得到DATA2第72～81发实测值与各个模型预测值,如表3所示,其时间序列关系曲线如图9所示。经过计算得到ARIMA模型预测值与DATA2第72～81发实测值的平均相对误差为0.123%,GM(1,1)模型预测值与实测值的平均相对误差为0.035%,一元线性回归模型预测值与实测值的平均相对误差为0.114%,组合模型预测值与预测值的平均相对误差为0.03%,小于1‰的误差标准,而且组合模型预测值与实测值的相对误差曲线如图10所示,可以看出每发预测值与实测值的相对误差均小于1‰,所以组合模型不论是整体的预测精度还是单项预测精度均达到了雷达测试弹丸径向速度的误差要求。

表3 DATA2第72～81发实测值与各个模型预测值

图9 DATA2第72～81发实测值与各模型预测值关系曲线

图10 DATA2组合模型预测值与实测值相对误差变化曲线

采用与预测DATA1同样的方法,得到了DATA3第42～51发实测值与各个模型预测值如表4所示,其时间序列关系曲线如图11所示。

表4 DATA3第42～51发实测值与各模型预测值

图11 DATA3第42～51发实测值与各模型预测值关系曲线

经过计算得到ARIMA模型预测值与DATA3第42～51发径向速度实测值的平均相对误差为0.014%,GM(1,1)灰色模型预测值与实测值的平均相对误差为0.062%,二次多项式回归模型预测值与实测值的平均相对误差为0.083%,组合模型预测值与实测值的平均相对误差为0.012%,所以组合模型预测的径向速度误差最小,精度最高,误差小于1‰,而且组合模型预测值与实测值的相对误差曲线如图12所示,均小于1‰,整体的预测精度和单项预测精度均达到了雷达测试弹丸径向速度的误差要求。DATA4第42～51发径向速度实测值与各个模型预测值如表5所示,其时间序列关系曲线如图13所示。ARIMA模型预测值与DATA4第42～51发径向速度实测值的平均相对误差为0.038%,GM(1,1)灰色模型预测值与实测值的平均相对误差为0.098%,二次多项式回归模型预测值与实测值的平均相对误差为0.085%,组合模型预测值与实测值的平均相对误差为0.015%,所以组合模型预测出的径向速度误差是最小的,精度是最高的,误差小于1‰,而且组合模型预测值与实测值的相对误差曲线如图14所示,单项误差也小于1‰,说明整体的预测精度和单项预测精度均达到了雷达测试弹丸径向速度的误差要求。

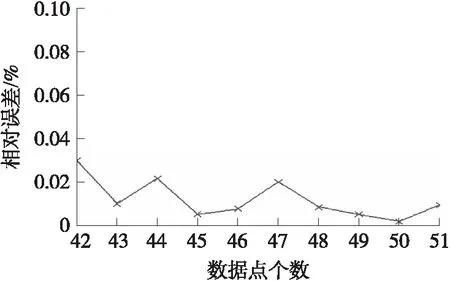
图12 DATA3组合模型预测值与实测值相对误差变化曲线

表5 DATA4第42～51发实测值与各个模型预测值

图13 DATA4第42～51发实测值与各个模型预测值关系曲线

图14 DATA4组合模型预测值与实测值相对误差变化曲线

通过利用DATA1、DATA2、DATA3和DATA4共4组实测数据进行建模预测的结果可知,3个单项模型预测径向速度的精度并不稳定,但组合模型预测弹丸径向速度的误差始终最小,精度始终高于所有单项模型,而且整体的误差和单项误差均低于1‰,预测值更加逼近试验中实测值,达到了雷达测试弹丸径向速度的误差要求,可以作为预测弹丸径向速度的预测模型。

实际上,样本量的选取完全是随机的,因为样本量越大,涵盖的数据特征就越多,模型的泛化能力就越强,而不同样本量对应的模型是一致的,建立的ARIMA模型都是ARIMA(1,0,0),GM(1,1)灰色模型和速度时间的回归模型都能通过检验,并且组合模型的预测精度始终大于单项模型。

4 结束语

径向速度的缺失会影响靶场试验对武器装备战斗性能的准确鉴定,利用科学合理的模型预测出缺失的径向速度显得至关重要。单一模型的预测能力有限,预测精度不够理想,组合预测模型能够充分发挥所有单项模型的预测能力,大幅度提高数据的拟合精度,可以最大限度提高预测精度。实验结果表明,经过对DATA1～DATA4 4组数据建模预测的结果可知,组合预测模型的预测精度最高,预测出的径向速度误差最小,整体误差和单项误差均小于1‰,达到了单台初速雷达测试弹丸初速的误差要求,可以作为弹丸径向速度的预测模型。