基于遗传算法的智能驾驶车辆纵向PID控制研究

康腾

（重庆交通大学 机电与车辆工程学院，重庆 400074）

主题词：智能驾驶车辆速度控制遗传算法PID控制

缩略语

PID Proportion Integration Differentiation

RBF Radial Basis Function

MPC Model Predictive Control

SMC Sliding Mode Control

GA Genetic Algorithm

ITAE Integrated Time and Absolute Error

1 引言

运动控制作为智能车辆研究的关键技术之一，是实现自动驾驶的关键环节，主要研究内容是根据运动规划输出和实时反馈的车辆行驶状态来控制底盘执行器的动作，使车辆稳定、平滑、精确地跟踪期望路径和轨迹。运动控制可分为横向控制和纵向控制，其中纵向控制主要是对加速和制动踏板进行控制，调节车辆按照规划速度进行加减速操作。根据实现方式的不同运动控制又可分为直接式和分层式2种控制方式。

目前常用的运动控制方法有比例积分微分控制（Proportion Integration Differentiation,PID）、模型预测控制（Model Predictive Control,MPC）和滑模控制（Sliding Mode Control,SMC）。其中PID控制具有不依赖于精确的系统模型、简单实用的优点，被广泛应用于智能驾驶汽车纵向运动控制。邓涛等针对纵向速度控制，采用了分层控制策略，上层模型预测控制器根据参考车速计算出期望加速度，下层控制器采用逆纵向动力学模型，计算得到期望的节气门开度或制动压力，达到跟踪车速的目的。在此基础上，Guo等采用自适应滑模控制器作为下层控制器，利用神经网络优化不确定项和变结构项，有效解决了被控系统参数不确定性、非线性和外部干扰的影响。Peng等设计了一种基于径向基函数神经网络的改进自适应滑模控制算法，仿真结果表明与传统滑模控制比,改进的算法具有更小的跟踪误差和更好的抗干扰性能。陈刚等提出一种基于非线性干扰观测器的模糊滑模车速控制方法，通过模糊控制规则来在线调节滑模控制的反馈增益系数，以此来减少抖振，同时用非线性观测器来估计和补偿模型的不确定性和外部干扰。Chen等将模糊控制算法与PID算法相结合，通过偏差和偏差变化率建立相应的控制规则，动态实时地对PID参数进行修正，仿真验证了算法的可靠性和鲁棒性。仝书杰设计了RBF-PID控制算法，通过在线系统辨识信息实现对PID参数的自适应调整，有效地处理了复杂的非线性系统。张严采用遗传算法优化模型预测控制器，得到车辆行驶时的最优时域参数，在减小车辆跟踪误差的同时提高了行驶稳定性。李广南等针对纵向速度控制提出了一种基于改进的粒子群优化算法的模型预测控制方法，仿真结果表明该算法有效提高了速度跟踪精度。

本文针对智能车变速下的速度跟踪精度提升问题，利用遗传算法优化PID控制器，得到不同速度下的最优控制参数，同时为简化模型计算，引入统一加速踏板概念，以统一加速信号，调节车辆执行加、减速操作，对车辆速度跟踪效果进行研究。

2 智能驾驶车辆纵向控制策略

本文建立了智能驾驶车辆纵向控制模型，如图1所示，上层控制器采用遗传算法对PID的3个参数进行优化，输入是参考速度与当前速度的差值e()，输出为期望的加速度，下层控制输入为上层控制器传来的期望加速度，输出为统一加速信号。即加速踏板信号和制动踏板信号用同一个控制量来表示，当统一加速信号为正时，车辆执行加速操作，当统一加速信号为负时，车辆执行减速操作。

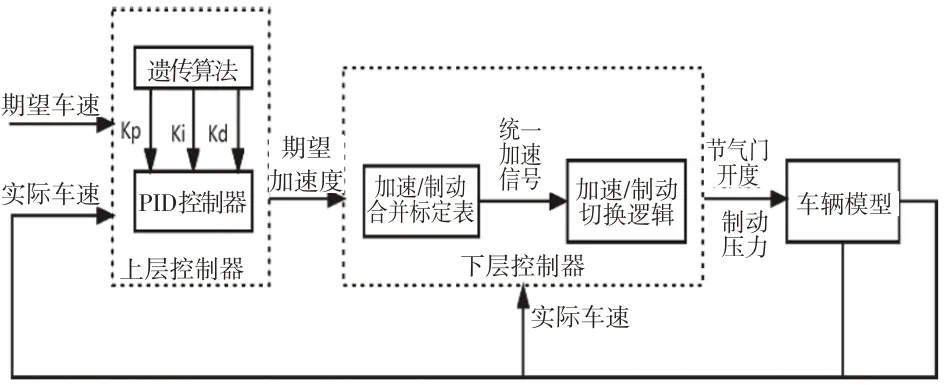
图1 纵向速度控制

上层控制器计算公式见式（1）～或（2）。

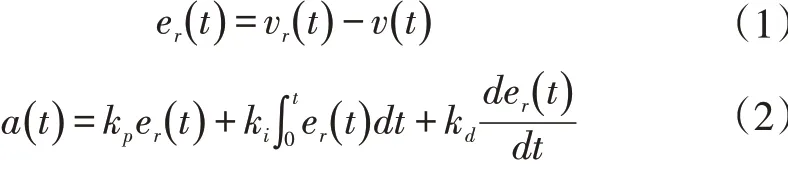
式中,时间；e()为速度偏差；()为输出的期望加速度；k,k,k分别为遗传算法优化后的比例系数、积分系数和微分系数。

3 纵向控制器的设计

PID控制器中，对比例参数、积分参数和微分参数进行优化具有重要意义，传统参数优化方法为人工根据经验调整参数值，不仅费时费力，而且还不能确保PID速度跟随控制器的跟随误差达到最小。基于此，提出利用遗传算法（GA）对PID的控制参数进行了优化设计，先利用GA对PID控制器的3个控制参数进行反复迭代训练，得到跟踪误差最小的一组参数，再将其作为PID的最优控制参数。目标函数评价指标采用时间乘以绝对值误差积分准则（ITAE），其表达式如式（3）：

式中，为速度随时间的累计误差，作为优化的目标函数。

3.1 遗传算法优化PID参数

3.1.1 算法原理

遗传算法是一类借鉴生物在自然界遗传和进化过程的全局优化算法，首先随机生成初代种群，进行基因编码，再根据适应度大小，从上代群体中按概率复制优秀个体进行交叉和变异，得到新一代种群，如此循环往复，最终算法会收敛到最好的染色体，也即问题的最优解。遗传算法可定义为一个8元组，见式（4）。

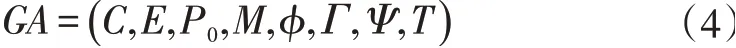
式中为个体编码方法；为个体适应度评价函数；为初始群体；为群体大小；为选择算子；为交叉算子；为变异算子；为遗传运算终止条件。本文采用二进制进行编码，适应度评价函数见式（5）。

式中，分母中为目标函数，0.001为经验设置，防止目标函数为零，出现无解情况。

3.1.2 算法改进

首先在进行复制操作时，为提升算法全局优化搜索的能力，以适应度由大到小对父代种群进行排序，选出前5个个体作为优秀个体,直接进入子代群体中，剩余个体以概率复制进入子代群体。其次在进行变异操作时，改变传统遗传算法以统一变异概率对任意染色体的任意一个或多个基因进行变异的做法，根据适应度大小来决定染色体上基因的变异概率。如该个体适应度越小，即其被选择的概率越小，则对该个体变异的概率就越大。最后在每完成一次遗传、交叉和变异操作后，将父代适应度高的个体赋值给子代对应位置，以保证子代个体适应度越来越高，直到迭代达到最优解。

3.1.3 GA-PID优化流程

GA-PID优化流程如图2所示。

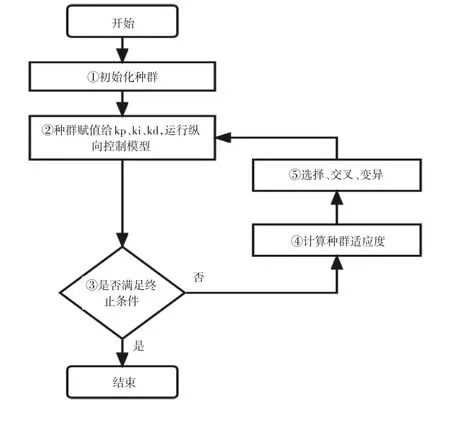
图2 遗传算法优化流程

遗传算法具体实现步骤如下：

步骤①：初始化种群，设置最大进化代数；

步骤②：将种群分别赋值给PID控制器3个控制参数,

结合当前车辆状态和参考信息，运行纵向控制模型，根据模型输出得到目标函数；

步骤③：判断迭代次数是否大于最大迭代次数，若满足就结束迭代，以进化过程中所得到的具有最大适应度的个体作为最优解输出，否则继续下一步；

步骤④：计算种群适应度。

步骤⑤：根据种群适应度大小进行复制运算，筛选出优秀个体，再进行交叉运算和变异运算生成新一代种群。

3.2 加速和制动标定

加速和制动的标定流程见图3。

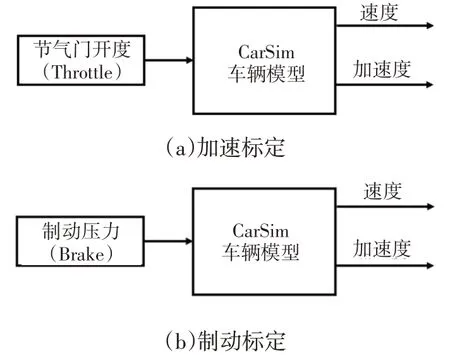
图3 加速与制动标定

将初速度设置为0 m/s，节气门开度范围为0～1。从0开始，开度每次增加0.05仿真一次，直到开度达到1结束，可以得到不同节气门开度下的速度和加速度曲线。将不同开度的节气门和对应的速度和加速度进行拟合，可以得到一个关于油门、速度和加速度的三维曲面（图4），曲面上每一个点(,,)就代表一个节气门，速度和加速度值。以不同速度和加速度对节气门开度进行标定，标定车速范围为0～50 m/s,标定加速度范围为0～5 m/s，标定公式如式（6）。

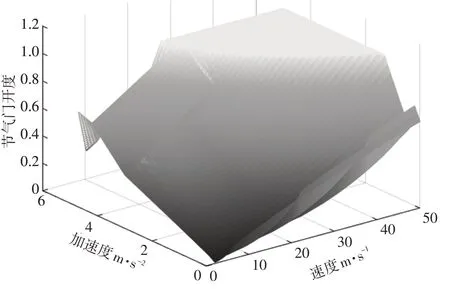
图4 加速标定三维图

式中，为节气门开度值;为车辆速度；为车辆加速度。

与加速标定同理，将初速度设置为50 m/s，制动压力范围为0～6 MPa，从0开始压力每增加0.1 MPa仿真一次，直到压力到达8 MPa时结束，可以得到不同制动压力下的速度和加速度曲线，将不同制动压力和对应的速度和加速度进行拟合，可以得到一个关于制动压力、速度和加速度的3维曲面（图5），曲面上每一个点(,v,a)就代表一个制动压力、速度和加速度值。以不同的速度和加速度对制动压力进行标定，标定车速范围为0～50 m/s，标定加速度范围为-8～0 m/s，标定公式如式(7)。

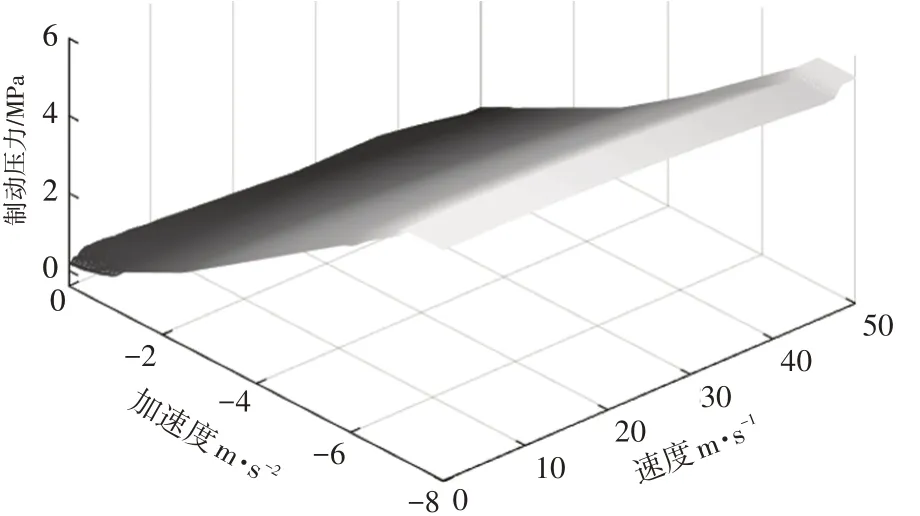
图5 制动标定三维图

式中，为制动压力值，为车辆速度，为车辆加速度。

4 仿真测试

4.1 恒定车速试验

将参考车速度设定为恒定的10 m/s，设置CarSim车辆模型的初速度为0，分别仿真纵向速度在经典PID控制和基于遗传算法优化的PID控制下速度的跟随情况。图6至图7所示为在恒定车速下2种控制器的跟随车速变化和跟随车速误差。由图6和图7可知，在恒定的参考车速下，与经典PID控制器比，本文设计的GA-PID控制器可以更快、更平稳的达到预期车速，同时在跟随过程中产生的速度误差更小，即控制精度更高，由此说明在恒定车速工况下，本文设计的控制器控制效果更好。

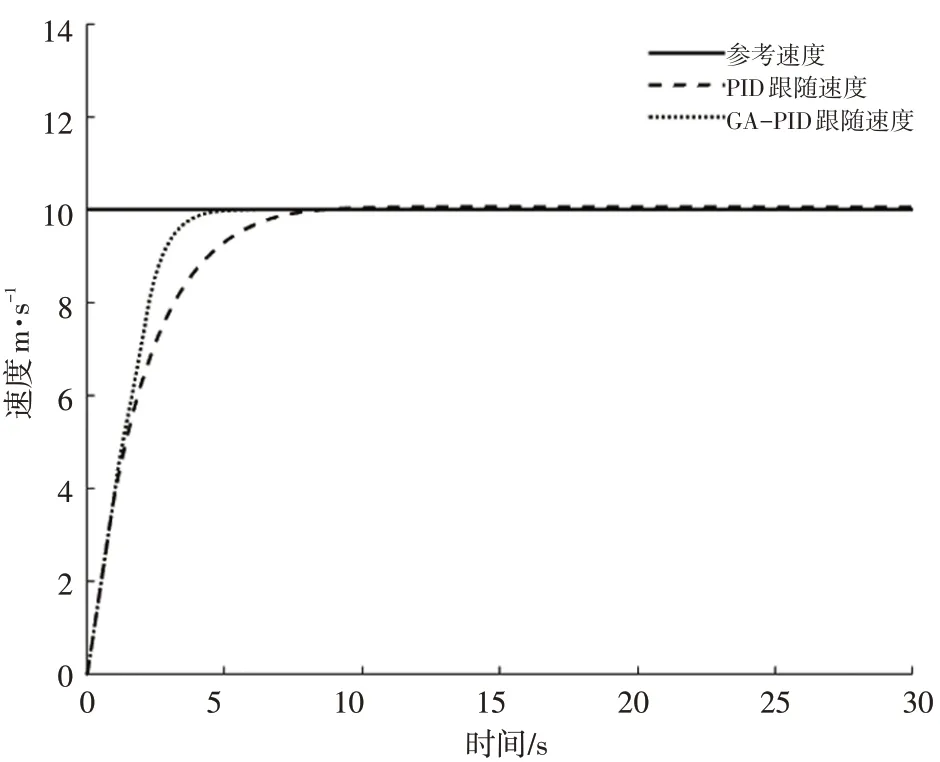
图6 恒速时控制器跟随车速

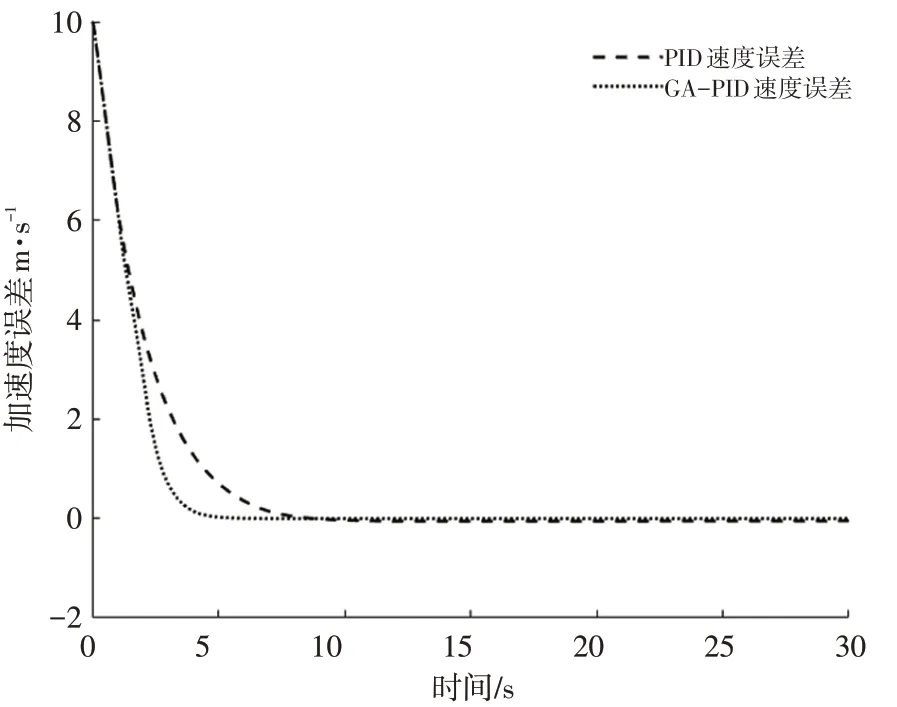
图7 恒速控制器跟随速度误差

4.2 变车速试验

车辆在行驶过程中速度往往随时都在变化，因此为了验证在速度变化时所设计控制器的跟踪效果，设计了一段包含匀速、加速、减速的参考速度曲线。图8至图10分别为参考速度变化时2种控制器跟随参考车速时的车速变化图、车速误差图和加速度变化图。由图8和图9可知，第1阶段匀速行驶时2种控制器的控制效果相差不大，在第2阶段加速行驶和第4阶段减速行驶时，GA-PID控制器都能更快的收敛到参考速度，第3阶段和最后阶段的匀速行驶，速度误差比经典PID控制器小，且控制过程平稳，超调量小。由图10可知，GA-PID控制器能更好地跟踪期望的加速度，且跟踪精度更高。由此说明在变速情况下，本文所设计的控制器控制效果也更好。

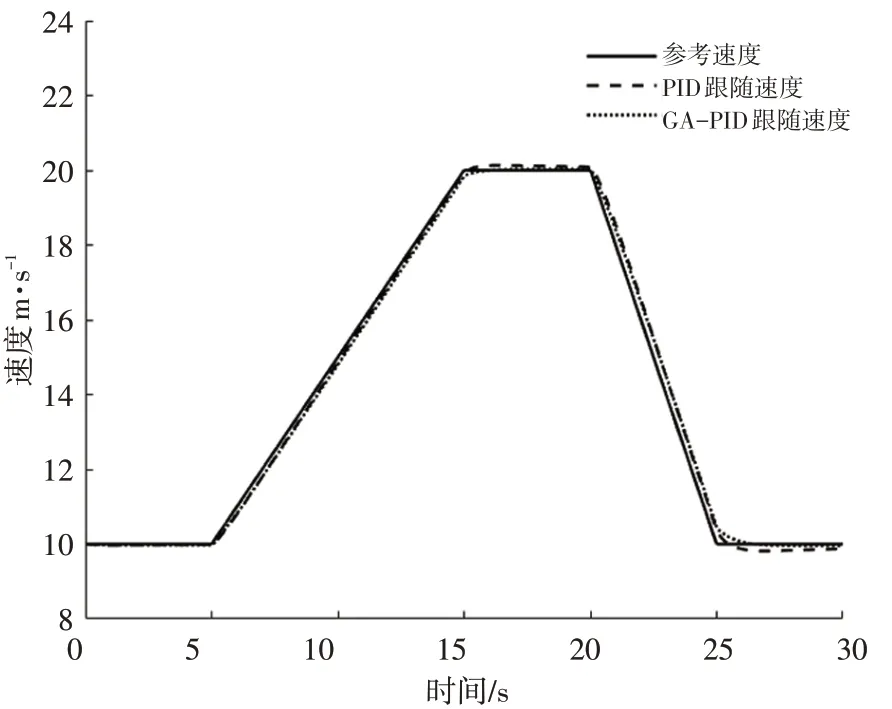
图8 变车速控制器跟随速度

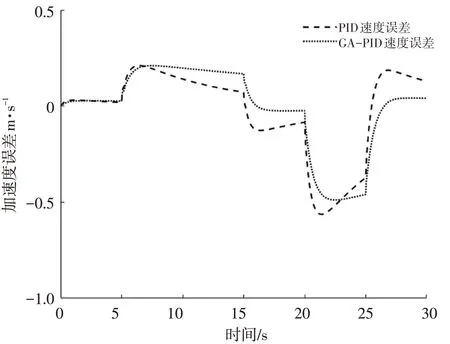
图9 变车速控制器跟随速度误差

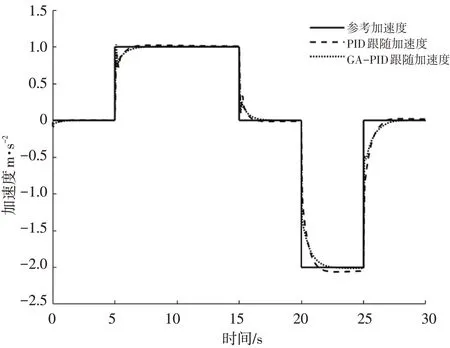
图10 变加速度控制器加速度变化

5 结束语

为提高智能驾驶车辆纵向速度跟踪精度，在经典PID控制的基础上，利用遗传算法对PID参数进行优化，使其能在不同的参考车速下得到最佳的期望加速度，基于试验标定得到节气门开度和制动压力。在Simulink/CarSim上建立了联合仿真模型，并进行了仿真验证，仿真结果表明：本文所设计的纵向控制器可以稳定快速地跟随期望速度轨迹，跟随过程中速度变化波动小，很好地保持了车辆在行驶过程中的稳定性。

目前智能驾驶车辆的研究大都将横向控制与纵向控制解耦单独考虑，在研究横向控制时，纵向车速通常设定为定值，在本文的基础上，未来可考虑将横向控制与纵向控制结合，实现变速情况下的智能驾驶车辆的横纵向综合控制。