含复合材料结构的非黏结柔性立管弯曲特性
2022-10-08刘庆升薛鸿祥袁昱超唐文勇
非黏结柔性立管被广泛应用于海洋油气业,常用于从海底到平台的油气资源传输,有时会根据设计的需要增加耐腐蚀、隔热层或是防止发生径向失效的复合材料圆柱壳层结构,例如,Epsztein等给出了含有耐HS气体腐蚀的复合材料层的非黏结柔性立管结构,Malta等给出含有以凯夫拉49复合材料构成的强结构带层,用于防止非黏结柔性立管发生轴向压力作用下的径向失效,但一般学者都直接将复合材料简化为各向同性材料或是等效为忽略复合材料圆柱壳层厚度变化的正交各向异性结构进行研究.非黏结柔性立管的中的螺旋层结构在弯矩载荷作用下可以克服层间的摩擦力并在层间自由滑动,导致其弯曲刚度具有高度非线性,一直以来是研究的热点和难点所在.基于一些严格的假设,一些学者给出了非黏结柔性立管的非线性弯曲模型.Féret等较早地给出螺旋条带弯矩-曲率迟滞曲线,但未考虑部分滑移阶段的弯矩-曲率关系.文献[5-6,9]基于功能原理给出了螺旋条带未滑移、部分滑移和完全滑移3个阶段的弯矩-曲率表达式.此后,Dong等在此基础上进一步给出了部分滑移阶段的弯曲刚度的显式表达式,并合理考虑了螺旋条带局部弯曲和扭转的影响.Ramos等也给出了螺旋条带未滑移和完全滑移阶段的弯曲刚度计算方法,可用于快速计算非黏结柔性立管未滑移和完全滑移阶段的弯曲刚度.与理论方法相比,数值和试验方法的相关研究相对较少.由于非黏结柔性立管造价较高,一般只有立管厂商会开展试验研究,但通常不会给出详细的立管参数.Witz在1996年开展了关于非黏结柔性立管截面力学性能的试验,不仅给出了详细的立管参数和试验结果,而且给出了试验的开展过程和边界条件,此后的理论和数值方法研究大都基于Witz的试验进行验证.数值方法经历了从等效简化数值模型到考虑非黏结柔性立管详细几何特性的数值模型发展,文献[4,16]都建立了考虑骨架层和抗压铠装层实际几何形状的数值模型,研究了非黏结柔性立管的弯曲特性.
以往研究大多只关注螺旋层结构的弯曲非线性模型,并将作用于非黏结柔性立管的轴对称载荷作为计算非黏结柔性立管层间接触压力的基础,而忽略了轴对称载荷对弯曲特性的影响,在立管的弯曲刚度较小时,作用于立管的轴对称载荷可能会对立管的弯曲特性产生较大影响.本文以一类8层的非黏结柔性立管为研究对象,考虑作用于非黏结柔性立管的轴对称载荷和弯曲载荷的联合作用,提出了一种轴对称载荷对非黏结柔性立管弯曲特性影响的理论模型.考虑了复合材料圆柱壳层结构对非黏结柔性立管弯曲特性的影响,通过将原防摩擦层结构替换为复合材料圆柱壳层结构,采用功能原理推导了轴对称载荷作用下计及复合材料层结构厚度变化的理论模型,在此基础上求解了非黏结柔性立管的层间相互接触压力,并推导出弯曲载荷作用下的理论模型.建立了含有详细几何特性的非黏结柔性立管数值模型,并进行了验证.基于本文提出的理论和数值方法,计算了含有复合材料圆柱壳层结构的弯曲特性,并分析了复合材料纤维体积分数对非黏结柔性立管弯曲特性的影响.
1 理论方法
1.1 复合材料层弹性常数计算
复合材料通常可以简化为正交各向异性的材料进行研究,基于复合材料截面的等应力假设可以求解复合材料的弹性常数,相应的推导过程可以参考Liu等的研究成果.
1.2 复合材料圆柱壳层在轴对称载荷作用下的理论模型
非黏结柔性立管轴对称载荷作用下的理论模型是弯曲载荷作用下理论模型的基础,需要基于轴对称载荷作用下的理论模型求解层间接触力,并基于该结果求解螺旋层结构的临界曲率,判断螺旋层是否发生滑移.本文对复合材料圆柱壳层模型进行了一定简化,忽略了复合材料的分层以及制造过程中的损伤,将宏观的复合材料圆柱壳层结构视为一个整体,在此基础上基于受力和变形关系推导相应的理论模型.
为了增强室内空间的自然感引入自然光,可以在一定程度上营造空间氛围。同时满足室内照明,减少人工照明,达到节能目的。然而,从理解上可以看出,注入自然光并不完美。在满足室内照明的同时,不可避免的会导致夏季室内温度上升,让人感觉不舒服,导致空调负荷增加。当然,这种矛盾也可以通过其他措施来解决。例如,它可以通过使用节能玻璃,或遮阳伞等来解决。



(1)
式中:
相应的外压载荷引起的弯矩可以表示为

、、为材料、、向弹性模量;为切变模量;相关参数为泊松比;和分别为内、外半径;为扭转惯性矩;为自定义的参数.
所谓“融合译法”即指在翻译含有“无灵主语”的英语句子时,先结合其他句子成分与语言表达习惯等进行通盘考虑,有时也需结合更大的篇章结构来考虑,再进行汉译。这样一来,英语的无灵主语便被融化合并在汉语的句子中。如下列所示:
其他层结构的平衡方程推导可以参考任少飞等的研究成果,此外,考虑层间的几何关系可以得到轴对称载荷作用下的平衡方程,求解层间接触压力大小.

1.3 复合材料圆柱壳层在弯曲载荷作用下的理论模型
先假设作用于圆柱壳层的轴对称载荷和弯曲载荷可以进行解耦,只考虑在单一方向的弯矩作用,并忽略圆柱壳层其他方向的曲率和挠率变化,相应受到的弯矩作用和曲率的关系可以简化为
=
(2)

(3)
式中:为惯性矩.
农村文化建设的主体是农民。对农民的培养,一方面需要科技培训,另一方面还要以人才引进为补充。科技培训着眼于现代农业发展的需要,人才引进则是避免出现城乡一体化建设中的管理不足。关于农民科技培训问题,国外的经验可资借鉴。韩、法两国非常重视农民的培训,兴办了许多农民技术学校,提高农业技术的同时,也开阔了农民的视野,更新了农民的观念。在人才引进方面,要注意文化“输血”和“造血”相结合,努力吸引人,留住人。〔5〕这样,农民的流动就会趋向正规化,从而降低农村离婚率,减少留守儿童和空巢老人,促进乡村振兴战略的稳定实施。
假设圆柱壳层结构在发生弯曲后,内外压力仍沿管长方向均匀分布,如图2所示,假设仅作用外压载荷,微元面积上受到的压力作用可以表示为
结合其他圆柱壳层的弯矩-曲率关系,并考虑螺旋层结构的未滑移、部分滑移和完全滑移阶段,建立非黏结柔性立管在弯曲载荷作用下的理论模型.
1.4 轴对称载荷与弯曲载荷联合作用下的理论模型
第二,对于3台冷却泵,通过远程后台监控系统,能够实现各水泵无间隙切换,同时可以监测水泵运行的温度、电流、压力等数据。
d=(+cos)dd
(4)
式中:为曲率半径;为绕圆柱壳层单元周向的角度;为圆柱壳层曲率中心到该位置的夹角.
“No! He was much bigger than that!” they cried.The Mother Frog puffed herself up even more.“Was he as big as this?” she asked in surprise.


o=0
假设作用于圆柱壳层结构的外力载荷为轴向力、绕中心轴转矩、内外压力和,如图1所示图中,、、方向分别为立管的周向、径向和轴向;′、′、′方向分别为立管受力变化后的坐标轴方向;定义该层结构的初始长度和轴向变化量Δ;平均半径和径向变化量Δ;厚度和厚度变化量Δ;绕轴扭转角度Δ通过胡克定律和功能原理可以求解轴对称载荷作用下的平衡方程:

忽略轴对称载荷引起的圆柱壳层结构的轴向伸长,假设圆柱壳层结构在轴对称载荷和弯曲载荷联合作用后各处曲率保持一致,如图3所示.图中,RP1和RP2分别代表圆柱壳层两端的几何中心端点;为曲率中心并考虑弯曲后的圆弧角度与曲率的关系为=,由轴对称载荷引起的对弯曲特性的影响可以表示为





(5)
对于单位长度的圆柱壳层结构,定义变量为

(6)
求解曲率0到1范围内的变量并进行线性拟合,得到如图4所示的曲线,忽略线性拟合后的曲线截距得到简化后的变量的表达式为
《卜算子》为双调小令,句式整饬。因缺乏长调慢词式的铺叙式的表情达意,词体格式、字数有限,所以作者为防在追求重复表达的同时给读者造成视觉上的审美疲劳,便在词调的谋篇布局上别出心裁,另辟蹊径。
(2)斜Y坡口焊接裂纹试验 试验标准:试验按照《焊接性试验斜Y坡口焊接裂纹试验方法》(GB4675.1—1984)进行。
≈0118
(7)
1.3.2 内置式反应堆制作。甜瓜、西瓜、红香芋反应堆制作分别是在种植行下挖宽0.4 m、深 0.25 m,宽0.6 m、深0.25 m,宽0.8 m、深0.2 m,长度与行长相等的沟,在沟内铺秸秆;然后将已扩繁的菌种均匀撒在秸秆上面(湿料1 kg/m2);撒好后用铁锹在秸秆上拍一遍,使菌种分散在秸秆里面;接着将开沟翻出来的2/3土覆盖于秸秆上,覆土时每隔1.5 m左右露出秸秆长度10 cm,以便输入氧气;然后将水注入沟内,水量充足,保证秸秆吸足;第2天,等到水充分下渗,再将余土覆盖秸秆,形成栽植垄,并撒上疫苗;最后合理布置滴灌设施,并及时覆盖地膜,促进种苗生长[3]。


=0118
(8)
同理可以推导内压和轴向力载荷的影响.
利用式(4)对角度和进行积分,可以得到微元上的压力在图2坐标轴各方向的分量:
2 数值方法
通过Abaqus软件建立了含有复合材料圆柱壳层结构的8层非黏结柔性立管数值模型,各层的剖面如图5(a)所示,完整的有限元模型示意如图5(b)所示.根据立管厂商的建议,为了减少边界效应的影响,非黏结柔性立管模型需要有足够的长度,通常为两倍的抗拉铠装层螺距的长度,本文数值模型长度为1 m,其中,骨架层和抗压铠装层结构计及了实际的截面几何形状(见图5(b)),非黏结柔性立管有限元模型整体包含超过30万个单元.在有限元模型两端建立两个几何参考点RP1和RP2,并将所有层截面的端点与之耦合,层间摩擦因数取为0.1.考虑到数值模型中存在大量的非线性接触的情况,以及尽可能真实地模拟非黏结柔性立管在复杂载荷作用下的结构响应,所有层结构都采用非协调体单元(C3D8I)进行模拟,并采用显式算法进行求解,采用通用接触模拟立管内部结构的复杂非线性接触.采用放大计算时间步的方法提高数值方法的计算效率,本文的最小时间步长取为5×10s,经验证,该时间步长可以在确保计算精度和稳定性的同时提高计算效率.同时,在复合材料圆柱壳层中定义局部柱坐标系赋予材料属性.采用准静态的方式对载荷进行加载,并释放如图5(b)中绕轴旋转的自由度,以及顶端RP1参考点的轴向(方向)自由度.非黏结柔性立管的几何和材料特性如表1所示,其中几何特性来自文献[14].


3 计算结果及分析
3.1 数值和理论方法验证
非黏结柔性立管在弯曲载荷作用下的理论模型以轴对称载荷作用下的理论模型为基础进行研究.首先通过轴对称载荷作用下的理论模型求解非黏结柔性立管不同层之间的接触压力,在此基础上求解螺旋层结构的弯曲临界曲率,之后加载弯矩载荷的作用,同时结合本文提出的轴对称载荷和弯曲载荷联合作用下的理论模型,求解非黏结柔性立管在未滑移、部分滑移和完全滑移阶段的非黏结柔性立管的弯曲特性.对于数值方法,载荷的加载方式与理论方法保持一致,同样地首先施加轴对称载荷,之后再在两端几何参考点RP1和RP2施加弯矩为的作用.采用显式算法进行求解时需要考虑惯性效应对结果的影响,因此本文采用准静态的方法对载荷进行加载,并模拟足够的加载时长以避免惯性效应可能对结果造成的影响,并始终控制动能与内能的比率在5%以内.
根据Witz试验对轴向张力作用下和弯曲载荷作用下的非黏结柔性立管特性进行验证.需要指出的是,Witz的弯曲试验中未施加轴对称载荷的作用,但是非黏结柔性立管由于制造过程中存在的初始缺陷等因素,层间始终存在初始的接触压应力作用,本文通过对最外部的护套层施加初始外压载荷,给出层间的接触压力作用,初始的外压载荷取为0.2 MPa,并先于弯矩载荷进行加载.
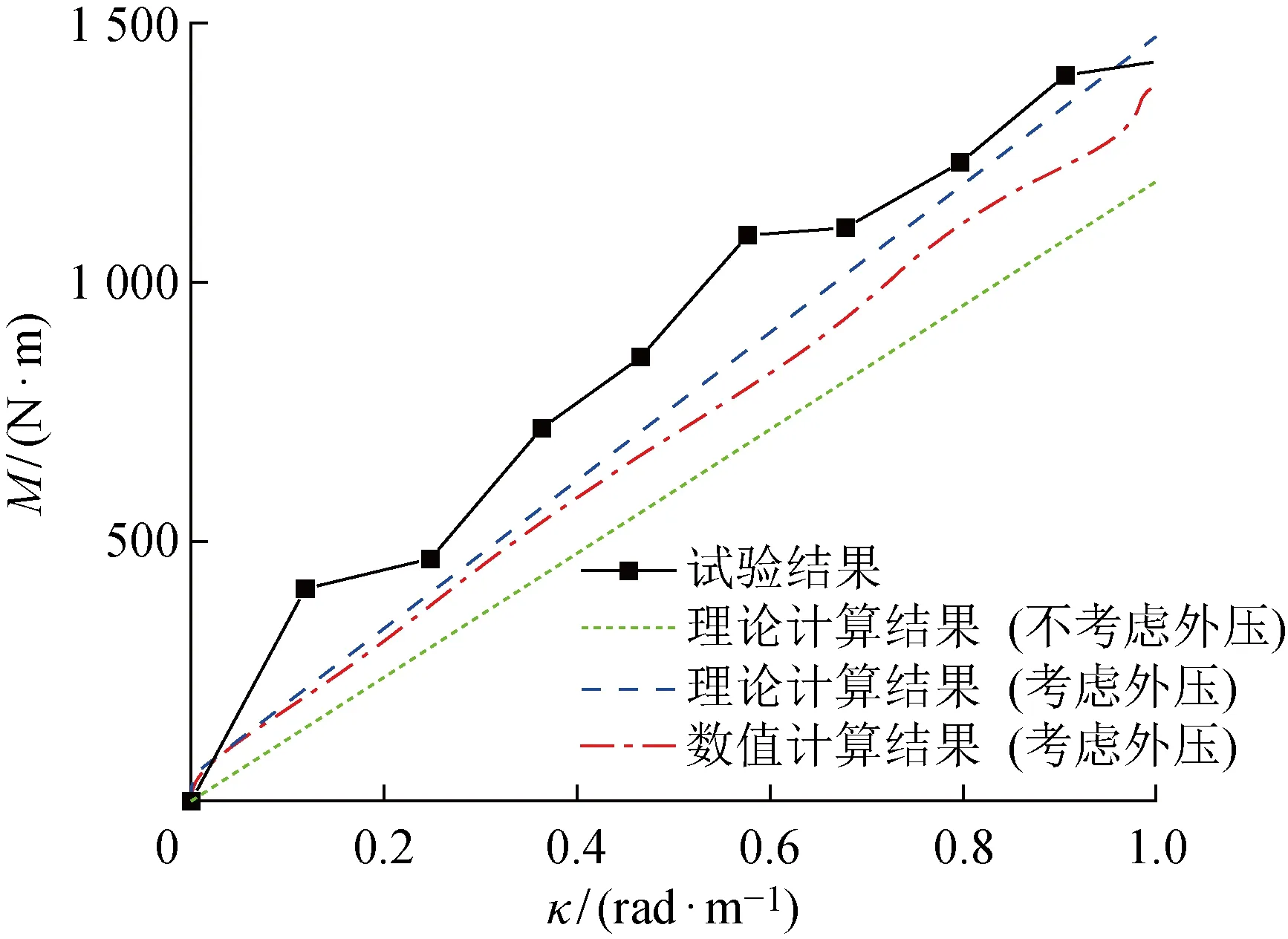
通过本文提出的理论和数值方法计算Witz试验中的工况,相应的计算结果如图6、7所示,得到相应的截面力学性能如表2所示,表中为抗拉刚度;为完全滑移阶段的弯曲刚度.从图7和表2中可以看出:轴对称载荷作用下的数值和理论方法吻合较好,且轴向延伸率随着轴向张力的增大基本呈线性变化,而试验结果存在一定的迟滞效应,将试验结果进行拟合得到的轴向抗拉刚度与本文的结果吻合较好,证明了理论和数值方法的有效性.在弯曲载荷作用下,分别通过理论方法计算了未考虑外压载荷和考虑外压载荷的情况,其中,考虑了外压载荷的完全滑移阶段的弯曲刚度与数值结果吻合较好,而未考虑外压载荷的弯曲刚度与试验结果吻合较好,侧面验证了本文数值方法的有效性.


需要指出的是,相比于数值方法,本文所提理论方法具有极高的计算效率,且可以得到与数值方法近似的计算结果.本文的数值方法在某具有48核的工作站上开展,弯曲载荷工况的载荷加载时间为 1.8 s,单一工况计算需要约72 h.本文的理论计算方法通过MATLAB软件进行编程,计算时间约为 15 s.
3.2 含复合材料圆柱壳层立管弯曲特性
选取两种海洋油气业常用复合材料替换原防摩擦层结构,相应的纤维和基体材料特性来自文献[18,24],整体材料特性如表3所示.两种复合材料的纤维体积分数()都在7%左右,其中,第1种材料以环氧树脂为基体,玻璃纤维为增强材料;第2种材料以高密度聚乙烯为基体,钢丝为增强材料,两种复合材料都表现出了明显的正交各向异性.
时值冬季,天气逐渐寒冷,宝宝稍不注意“小肚子”就会着凉,尤其是年龄较小的宝宝,拉起肚子来往往让宝妈们措手不及又心疼不已。

同样对于含有复合材料圆柱壳层的非黏结柔性立管模型首先施加0.2 MPa的外压载荷作用,之后在模型的两端几何参考点施加弯矩,求解弯曲特性.以含有复合材料1的非黏结柔性立管模型为例,分别给出模型在仅加载外压载荷以及加载外压和弯矩耦合载荷作用时外部抗拉铠装层结构在立管轴向的应力()云图,如图8所示.图8(a)为立管在仅施加外压载荷时的应力云图,可以看出应力在立管轴向方向并未完全均匀分布,但数值计算结果比较稳定,外压载荷和立管的轴向位移基本呈线性变化,在外压加载结束后,非黏结柔性立管的轴向延伸率仅为 -0.010 5%,对计算曲率影响较小,可以在计算时忽略.图8(b)给出了在外压载荷和弯矩载荷联合作用下的应力云图,可以看出螺旋条带有着明显的弯曲变形,边界处有明显的应力集中现象,此外,与理论方法的假设一致,单一螺旋条带的应力沿着其轴线方向呈现周期性变化.分别通过本文提出的理论和数值方法求解含有复合材料圆柱壳层的非黏结柔性立管的弯矩-曲率曲线,相应的计算结果如图9所示,可以看出数值方法计算得到的未滑移和部分滑移阶段不明显,但在完全滑移阶段理论结果和数值结果吻合较好,相应的完全滑移阶段的弯曲刚度计算结果如表4所示.对比原非黏结柔性立管模型,强度较高的复合材料会对弯曲刚度增强较大,相应的弯曲变形减小.同时,给出各层结构对非黏结柔性立管整体的弯曲刚度贡献,如表5所示.可以看出,复合材料圆柱壳层结构贡献了大部分的非黏结柔性立管模型整体的弯曲刚度,在承受弯矩载荷作用时,含有轴向强度较高的复合材料圆柱壳层结构的非黏结柔性立管模型将不再容易发生大挠度弯曲变形.




3.3 纤维体积分数的影响分析
考虑纤维体积分数对含有复合材料圆柱壳层的非黏结柔性立管弯曲特性的影响,选取几种海洋油气业常用的增强纤维材料进行研究,包括常用于组成防止非黏结柔性立管发生径向失效的强结构带的凯夫拉49增强纤维,所有的基体材料都采用环氧树脂,相应的材料参数如表6所示.

考虑复合材料圆柱壳层的纤维体积分数从0%至70%变化,通过理论方法计算不同纤维体积分数的复合材料对非黏结柔性立管完全滑移阶段弯曲刚度的影响,结果如图10所示.从图中可以看出,含有复合材料圆柱壳层的非黏结柔性立管完全滑移阶段的弯曲刚度随着纤维体积分数的增大接近线性增长,但与原非黏结柔性立管模型相比,完全滑移阶段的弯曲刚度已经发生了巨大的变化,在复合材料材料强度最大的工况(普通碳纤维材料,纤维体积分数为70%),相应的完全滑移阶段的弯曲刚度为 176.78 kN·m,远大于原含有防摩擦层非黏结柔性立管模型完全滑移阶段的弯曲刚度.
综合,俯卧位机械通气有利于改善重症肺炎并呼吸衰竭患者的PaO2、Pa O2/FiO2、SaO2,且对血流动力学无明显影响,值得临床推广。

同时,以碳纤维复合材料为例,考虑含有不同纤维体积分数复合材料圆柱壳层结构的非黏结柔性立管模型的轴向抗拉刚度的影响,给出轴向抗拉刚度与完全滑移阶段的弯曲刚度的关系,如图11所示.从图中可以看出,不同含有纤维体积分数复合材料圆柱壳层非黏结柔性立管的轴向抗拉刚度和完全滑移阶段的弯曲刚度正相关,但完全滑移阶段的弯曲弯曲刚度比轴向抗拉刚度对纤维体积分数更敏感,以碳纤维复合材料为例,当纤维体积分数从0%至70%变化时,轴向抗拉刚度增大了116.29%,而完全滑移阶段的弯曲刚度增大了 3 582.92%.

4 结论
采用复合材料圆柱壳层结构替换了原非黏结柔性立管中的防摩擦层结构,考虑复合材料的材料特性,并基于功能原理推导了复合材料圆柱壳层结构在轴对称载荷作用下的平衡方程,在此基础上推导了含有复合材料圆柱壳层结构在弯曲载荷作用下的理论方程,提出了施加于非黏结柔性立管的轴对称载荷和弯曲载荷联合作用的理论模型,同时建立了相应的含有详细几何特性的数值模型,并通过与试验结果进行对比验证了所提方法的准确性.本文提出的理论模型可以有效地解释轴对称载荷和弯曲载荷的联合作用,并快速地计算得到复杂载荷作用下的非黏结柔性立管的结构响应,准确地计算得到复杂载荷作用下的非黏结柔性立管的弯曲特性.主要结果有:
(1) 外压载荷会增大非黏结柔性立管的弯曲刚度.
(2) 采用强度较高的复合材料替换原防摩擦层结构,非黏结柔性立管的完全滑移阶段的弯曲刚度会有较大提升,并且不再容易发生大挠度弯曲变形.
(3) 复合材料的纤维体积分数对含有复合材料圆柱壳层结构的非黏结柔性立管的轴向抗拉刚度和完全滑移阶段的弯曲刚度都有一定提升,并且随着纤维体积分数增大,两种截面力学性能都基本呈线性变化.
(4) 完全滑移阶段的弯曲刚度对复合材料纤维体积分数的敏感性较高,轴向抗拉刚度对复合材料纤维体积分数的敏感性较低.
