减振垫层温频变动力性能对无砟轨道振动特性影响
2022-10-08牛振宇刘林芽秦佳良左志远
随着我国高速铁路的快速发展,无砟轨道技术已广泛应用于高速铁路中.CRTSIII板式无砟轨道系统是我国具有完全自主知识产权的无砟轨道系统,但高速铁路技术迅速发展的同时也伴随着振动和噪声的出现.针对这一问题,我国高速铁路行业在吸取城市轨道减振降噪经验的基础上,研发了减振型 CRTSIII 板式无砟轨道并取得了显著的减振降噪效果.该类型轨道结构通过布置减振垫层来达到减振的目的,减振垫层是该类型轨道结构中具有弹性和阻尼性能的部件,其动态力学性能对车辆-轨道耦合系统振动响应有着重要的影响.减振垫层由黏弹性橡胶高分子材料制成,高分子材料的动力学行为往往随环境温度以及加载频率非线性变化,同时表现出黏性液体和弹性固体的力学特征,即黏弹性力学特征.用于描述橡胶高分子材料的动力特性最基本的两种模型是Maxwell模型和Kelvin-Voigt(K-V)模型.这两种模型均属于标准机械模型,简单直观,但是由于其导数阶数均为整数,模型不能反映加载历史的影响,难以准确描述减振垫层的频变特性.
分数阶导数模型是在标准机械模型的基础上进一步发展而来的,其导数阶数为分数,因此该模型能够考虑加载历史的影响,准确体现橡胶材料的频变特性.赵永玲等对橡胶材料频变特性进行对比分析,结果表明:分数阶K-V模型在描述橡胶材料频变特性存在一定的误差,而高阶分数阶导数FVMP模型能较好地描述橡胶材料的频变特性.在车辆-轨道耦合系统的分析中,通常将减振垫层简化为线性弹簧和黏性阻尼并联的K-V模型,但是K-V模型不能真实地反映减振垫层的频变特性.Zhu等将描述扣件胶垫频变特性的分数阶K-V模型应用到车辆-轨道耦合系统动力学模型中,对比分析了扣件胶垫的频变特性对轮轨系统动态响应的影响.Yang等采用分数阶Zener模型对扣件胶垫宽频动力性能进行预测和表征,取得有效的预测效果,并将表征扣件胶垫频变特性的分数阶Zener模型和幅变特性的Berg模型应用于车辆-轨道耦合系统动力学模型中分析扣件胶垫黏弹塑性对车-轨耦合振动响应的影响.
上述研究对于扣件胶垫频变特性已有较为深入的探讨,但是对于减振垫层的研究一般仍采用K-V模型来替代,鲜有文献考虑减振垫层的温频变特性对轨道结构的影响.鉴于此,本文以减振型 CRTSIII 板式无砟轨道减振垫层为研究对象,通过动态力学性能试验结合温频等效原理得到减振垫层温频变力学特性,并采用能在较宽加载频率范围内描述减振垫层频变力学特性的高阶分数阶导数FVMP模型来建立减振垫层数学模型,将其嵌入车辆-轨道垂向耦合模型中,计算出轨道结构各部分的振动响应,从而研究减振垫层温频变特性对轨道结构振动响应的影响.
1 减振垫层FVMP模型与其动态力学性能试验
用EPLEXOR 500 N动态黏弹谱仪进行动态热机械分析(Dynamic Thermomechanical Analysis, DMA )试验,以减振型CRTSIII板式无砟轨道使用的减振垫层橡胶垫为试验对象,为满足DMA试验机对试件尺寸的要求,减振垫层橡胶垫选用直径为 10 mm、厚为10 mm的圆柱体作为试验试件.橡胶垫制作3组试件,进行平行试验.给橡胶垫试样施加预荷载后,进行加载频率为2 Hz,温度为 -60~40 ℃ 的扫描试验,试验设置仪器的升温速率为 2 ℃/min.台阶升温中,每个台阶高度为2 ℃,恒温时间300 s,测定试样的荷载-位移响应随温度的变化,最终获取橡胶垫动参数的温度谱如图1所示.图中:为模量,为温度,为损耗因子.分数阶导数模型因具有参数少、精度高等优势,被众多学者采用.在分数阶导数模型中,相比于仅有1个导数阶数的低阶分数阶导数模型,高阶分数阶导数模型不仅可以在中低频范围内描述减振垫层的频变特性,在高频条件下也能进行准确表征.FVMP模型是高阶分数阶导数模型中常用的一种模型,能够用 7个参数在较宽的加载频率范围内准确描述减振垫层动参数的频变特性,其时域本构方程为


(1)
=,=
式中:、为FVMP模型的黏性系数;()为减振垫层弹性力;()为减振垫层位移;、、为分数阶微分算子;、、为分数阶导数阶数;、为FVMP模型的弹性系数.
对式(1)进行傅里叶变换后,经整理可得到FVMP模型确定的复模量:
式中:为轨道板质量;()为轨道板正则振型坐标;为自由梁正交函数系内的常数;为轨道板弹性模量;为轨道板截面惯量;为轨道板长度,则轨道板可以分为段;为钢轨计算长度, 可参考文献[14]确定,本文取196 m;rs()为第个扣件支点的反力;∈[(-1),];为该轨道板上的扣件支点个数;为轨道板所选取的广义坐标个数.


(2)
式中:()为时刻减振垫层的位移量;Δ为积分时间步长,本文取其值为1×10s;为时刻之前的积分步数,对于的取值,Spanos等指出,在计算分数导数算子时,只需要考虑当前时间步之前160步即可得到满意的结果,本文取160;为累加求和的累加计数符号工具;+1、+1、+1和+1为减振垫层FVMP模型的Grünwald系数.
由图5(a)可知,钢轨垂向位移各工况的频域响应在1~250 Hz频段内基本一致,而在250 Hz之后的频段内则存在一定的差别,其中FVMP模型 20 ℃ 下的频域响应大于K-V模型20 ℃下的频域响应;FVMP模型各参考温度点在该频段内的响应表现为随着温度的降低而减小的趋势.由图5(b)可知,钢轨垂向振动加速度各工况的频域响应在1~200 Hz频段内基本一致,而在200 Hz之后频段内则存在一定的差别,在中高频段内差别尤为明显,其中FVMP模型20 ℃下的频域响应大于K-V模型20 ℃下的频域响应;FVMP模型各参考温度点在该频段内的响应表现为随着温度的降低而减小的趋势.

(3)

青辰被重重地扑倒在地,土狼王宽大厚重的前爪,像铁钳一样压在了他的双肩,粗长锋利的爪尖,直接按进了他的肩膀,令他痛得几乎昏厥。他发出一声怒吼,来驱散那些快速向着灵魂渗透而来的恐惧,并唤醒自己的热血和筋肉。他拼尽全力,架起双臂,一只手扣住了敌人的脖颈,另一只手则扒住了敌人的嘴。这样剧烈的动作,令利爪下的肩膀,留下了更深更大的伤口,鲜血奔洒而出。

(4)
=()()
式中:为广义速度矢量;为广义加速度矢量;和为积分常数,研究表明当==12时,显式积分法具有良好的稳定性和较高的精度;下标-1、和+1 分别代表第-1、和+1个子步.初始条件设为
(5)
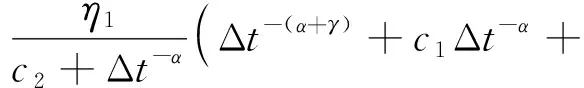
《中国留学发展报告(2017)蓝皮书》指出,根据教育部最新数据,2016-2017年,我国留学海归已达到43.25万人,超过8成留学生学成后选择回国发展,较之前一个学年增加了2.08万人,同比增长3.97%。留学人数增速放缓,低龄留学热潮,中外合作办学迅速发展等都成为了中国留学发展的新特点。[1]



由图2可知,高阶分数阶导数FVMP模型能很好地对减振垫层的动参数进行拟合,对于减振垫层的储能模量和损耗因子,在K-V模型下显示其为不随温度和加载频率变化的常数,与试验值相比显然存在较大的偏差,而FVMP模型对于各参考温度点下储能模量和损耗因子随频率的变化则可以较好地拟合.减振垫层的动参数与温度和加载频率有明显的相关性.相比于加载频率,温度对减振垫层动参数的影响更为显著.但在大多数的车辆-轨道耦合模型仿真计算中,常将其看作是不随温度和加载频率变化的常数,这必然是不合理的,高阶分数阶导数FVMP模型计算的动参数与试验数据吻合度较好,这是由于本模型具有3个分数阶导数阶数、、,能够精确描述减振垫层动参数的频变特性.

2 车辆-轨道垂向耦合振动分析模型
通过前述试验分析,得到了减振垫层力学性能的温频变规律,并使用高阶分数阶导数FVMP模型对其频变特性进行了表征.采用我国CRH380型高速客车与减振型CRTSIII型板式无砟轨道结构,首先进行车辆-轨道垂向耦合动力学模型的建立,如图3所示.其中,自密实混凝土和底座板之间的联结选用高阶分数阶导数FVMP模型,即将高阶分数阶导数FVMP模型带入所建立的垂向耦合模型中,从而进行减振垫层温频变特性对轨道结构振动响应影响的计算和分析.图中:、为车体的沉浮和点头;、为2个转向架的沉浮;、为2个转向架的点头;、、、为4个车轮的垂向位移.
2.1 车辆模型
车辆系统采用半车车辆模型,此模型考虑的车体运动状态有、、、、、、、、、共10个自由度.
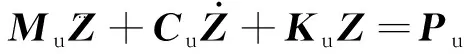
(6)
式中:、和分别为车辆系统的质量矩阵、阻尼矩阵和刚度矩阵;为车辆系统的位移矢量;为轮轨作用力.
2.2 轨道模型
在板式无砟轨道中,轨道振动主要体现在钢轨和轨道板的振动.本文轨道子模型采用如图3所示的减振型 CRTSIII 型板式无砟轨道模型.钢轨采用离散点支撑欧拉梁模型,该欧拉梁模型的边界条件需要满足车辆第1轮对激振点和第4轮对激振点至前后钢轨简支端的距离不低于30 m的条件,钢轨振型坐标二阶常微分方程组的基本形式见文献[14].钢轨与轨道板采用离散分布的弹簧-阻尼单元.轨道板与自密实混凝土考虑为同一参数的模型,模型采用自由梁模型,由减振垫层支撑,轨道板的垂向振动微分方程见文献[14],基础采用路基形式.
2.3 高阶分数阶导数FVMP模型的应用
图3是将高阶分数阶导数FVMP模型应用于车辆-轨道垂向耦合系统中的物理模型.在传统的车辆-轨道垂向耦合模型中,减振垫层常使用线性K-V模型,该传统模型下的减振垫层支反力如下:

(7)
式中:、分别为轨道板下减振垫层沿长度方向的分布刚度和分布阻尼;(,)为轨道板的振动位移;为具体时刻下的垂向位移.
本文所使用的高阶分数阶导数FVMP模型对应的减振垫层支反力计算过程如下.
式(1)为本文高阶分数阶FVMP模型的时域本构表达式,对(1)式进行数值求解,采用Grünwald-Letnikov定义可得到本文所使用的高阶分数阶导数FVMP模型对应的减振垫层支反力表达式:



(8)
利用减振垫层DMA试验结果并基于温频等效原理,可将减振垫层动参数随温度变化的曲线转化为不同参考温度点下减振垫层动参数随加载频率变化的频变曲线,如图2所示.结合式(3)~(5),通过利用最小二乘法及遗传算法对FVMP模型参数进行识别.本文给出了40、20和-40 ℃共3个参考温度点下的频变曲线以及预测结果,由此即可确定高阶分数阶导数FVMP模型的参数值,如表1所示.


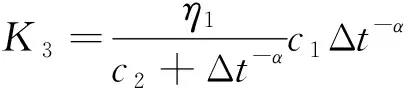




式(8)中代表减振垫层位移量的()可以替换为代表轨道板位移量的(,)将式(8)带入文献[14]中轨道板的垂向振动微分方程可得到减振垫层使用FVMP模型的轨道板振型坐标二阶常微分方程组的详细表达式:

在我把行李打包完毕时,我不禁揣想起来,弟弟给我们父母的棚屋装满瓶装水、蜡烛和罐头食品的古怪爱好是如何转变成一处能避开放射性落尘的避难所的部分所有权的。
2.4 数值积分方法
车辆系统与轨道系统的相互耦合应用Hertz非线性弹性接触理论来确定轮轨之间的垂向作用力.由此可得到减振垫层应用高阶分数阶导数FVMP模型的车辆-轨道垂向耦合模型.对各个子系统的振动方程进行矩阵形式的书写,最终得到处理成矩阵的形式:
桑:写作是将内心世界向外部世界推进的一种手段,是一种巨大的幸福,是一种奇妙的解脱和真正的生活。这当中,我拒绝一切陈规俗律的束缚,不顾一切,不惜任何代价地写作,你无法想象我有多么狂热地爱着《德克萨斯》,《德克萨斯》是我在最美的岁月中用灵魂创作的一部作品,倾注了我所有的情感与思想。它将是我一生的珍藏,我只将它献给我最爱的人。我希望我的痴心倾注,能赋予作品一种内在激情及真实性。

(10)

1.1 材料 ①一次性无纺布,规格120 cm×120 cm、60 cm×60 cm各60块;②双层棉布,规格120 cm×120 cm、60 cm×60 cm各60块(在包布一角订一块3 cm×3 cm的“补丁”,用于记录使用次数);③3M压力蒸汽灭菌化学指示卡及指示胶带。
对于求解该大型非线性运动微分方程组,本文采用新型显式积分法:

(11)
3.培训需求预测分析的核心在于确认差距。其核心是通过对被培训者现有状况和理想状况的调查与分析,确定二者的差距,为确定是否需要培训及需要培训的内容提供依据。
===
3 减振垫层温频变特性对轨道结构振动响应的分析
3.1 计算参数
车辆计算参数由文献[13]给出,轨道结构计算参数如表2所示,其中减振垫层选择在温度20 ℃、加载频率4 Hz下的刚度系数和阻尼系数作为K-V模型的动参数,减振垫层温频变参数由表2减振垫层FVMP模型动参数给出.

3.2 减振垫层频变特性对轨道结构振动响应的分析
以我国高速铁路无砟轨道不平顺谱作为轮轨系统输入激励,行车速度设为350 km/h.为了研究减振垫层温频变特性对轨道结构振动响应的影响,进行4种工况的设计,如表3所示,从而对比分析减振垫层常量动参数与温频变动参数对轨道结构振动响应的影响.时域响应中4种工况的对比,如图4所示,图中、、和分别为钢轨垂向位移、钢轨垂向振动加速度、轨道板垂向位移和轨道板垂向振动加速度.对图4进行傅里叶变换以及1/3倍频不计权处理,所得结果如图5所示.图中,r、r、g、g分别为钢轨垂向位移频域响应、钢轨垂向振动加速度频域响应、轨道板垂向位移频域响应、轨道板垂向振动加速度频域响应.


由图4可知,相比于K-V模型20 ℃下的响应,在时域响应中FVMP模型在20 ℃下的钢轨垂向位移和钢轨垂向振动加速度的响应差别较小,其各峰值分别相差3.93%和0.39%,而轨道板垂向位移和轨道板垂向振动加速度在两种工况下响应的差别则较大,其峰值分别相差17.97%和146.29%.由图4(a)与4(c)可知,FVMP模型在各参考温度点下钢轨与轨道板垂向位移的响应都呈现出随着温度的降低而减小的趋势,相比40 ℃的响应,在20 ℃和 -40 ℃ 下钢轨垂向位移的响应分别减小了2.26%与11.51%,轨道板垂向位移分别减小了8.77%与43.37%,其原因在于减振垫层的刚度随着温度的降低而增大,从而导致低温下的位移响应较小.由图 4(b) 与4(d)可看出,FVMP模型在各参考温度点下钢轨与轨道板垂向振动加速度的响应都呈现出随着温度的降低而增大的趋势,相比于40 ℃的响应,在20 ℃和 -40 ℃ 下钢轨垂向振动加速度分别增大了0.41%与1.14%,轨道板垂向振动加速度分别增大了6.72%与22.22%.


选择我院自2017年1月—2017年12月收治的53例经手术病理确诊的原发性肝癌患者作为研究对象,其中男性40例、女性13例,患者年龄分布:28~80岁,平均年龄(55±12)岁,诊断前患者均神志清醒,能够配合完成呼吸指令和CT增强扫描,且均无碘过敏反应史。
由图5(c)和图5(d)可知,轨道板垂向位移与垂向振动加速度分别在1~12 Hz和1~16 Hz的频段内都呈现出K-V模型在20 ℃下的频域响应大于FVMP模型20 ℃下的频域响应,而分别在12 Hz与16 Hz之后频段呈现出相反的趋势,在中高频段内尤为明显,如对于轨道板垂向位移在800 Hz时两工况下的频域响应分别为5.94与23.95 dB,对于轨道板垂向振动加速度在1250 Hz时两工况下的频域响应分别为28.59与57.2 dB.这是由于K-V模型在高频段内过高估计减振垫层的阻尼,使得其计算得到轨道板垂向位移响应小于FVMP模型计算的结果.
对于轨道板垂向位移与垂向振动加速度在FVMP模型各参考温度点下的响应,分别表现为在1~230 Hz和1~200 Hz频段内的响应都表现为随着温度的降低而增加的趋势,且在低频段内尤为明显,且都在230 Hz之后的中高频段内呈现出相反的趋势,在高频段内较为明显.如对于轨道板垂向位移在1250 Hz时FVMP模型在40、20和-40 ℃下的频域响应分别为23.88、22.13和13.95 dB;对于轨道板垂向振动加速度在1600 Hz时FVMP模型在40、20和-40 ℃下的频域响应分别为60.62、56.22和48.96 dB.
乌云其木格:关于水费收补问题的矛盾前面已经涉及了,我想回答的时候侧重于重点时间表。另外,用哪些手段如期实现。
综上所述,针对轨道结构振动响应的分析,考虑减振垫层温频变特性相比于不考虑时有较大差异,轨道板尤为明显.因此在进行仿真分析时,为提高对轨道结构预测的准确性,有必要考虑减振垫层的温频变特性.
小儿推拿学的生理特点主要有脏腑娇嫩、形气未充——五脏六腑稚阴稚阳、元气不足—脾气、肺气、肾气不足,心肝有余;生机勃勃,发育迅速;发病容易,转化迅速;脏气清灵,易趋康复。可预防治疗常见病,包括:小儿泄泻、呕吐、食积、厌食、便秘、腹痛、脱肛、感冒、咳嗽、哮喘、发热、遗尿、夜啼、肌性斜颈、落枕、惊风等疾病,都有较好的效果。
【文化说明】习语talk turkey源于美国民间传说。相传北美殖民时期,一个白人和一个印第安人一同打猎,事先商定要平分猎物。他们打到了两只火鸡和三只乌鸦(另一说是红头美洲鹫(buzzard)。白人把乌鸦都给了印第安人,把火鸡全留给了自己。印第安人反对,白人说:“You have three birds, I have only two.”(你分了三只鸟,我只有两只。)印第安人回答说:“Stop talking birds. Talk turkey.”(别说鸟,说火鸡。)
4 结论
本文针对减振型CRTSIII型板式无砟轨道结构的减振垫层,采用高阶分数阶导数FVMP模型代替传统的K-V模型,通过试验得到减振垫层的温频变特性,并建立了的车辆-轨道垂向耦合模型,从而在此基础上分析了减振垫层温频变特性对轨道结构振动响应的影响,得到如下结论:
[8] The White House Office of the Press Secretary, President Donald J. Trump’s Summit Meeting with Prime Minister Shinzo Abe of Japan, November 6, 2017, https://www.whitehouse.gov/the-press-office/2017/11/06/president-donald-j-trumps-summit-meeting-prime-minister-shinzo-abe-japan.
(1) 减振垫层的动参数对温度和加载频率有明显的依赖性,高阶分数阶导数FVMP模型能在宽频段内描述减振垫层的动态力学行为.
(2) 考虑减振垫层的温频变特性对轨道结构垂向振动响应有很大的影响,其中轨道板尤为明显,在时域响应中,对于轨道板位移和轨道板加速度在FVMP模型20 ℃下计算的峰值明显大于K-V模型20 ℃下的峰值.对于FVMP模型在各参考温度点下轨道板位移的响应呈现出随着温度的降低而减小的趋势,而轨道板加速度则呈现出随着温度的降低而增大的趋势.
(3) 在低频段内轨道板的响应表现为K-V模型20 ℃下的频域响应大于FVMP模型20 ℃下的频域响应,而在中高频段内则表现为相反的趋势.FVMP模型各参考温度点在低频段内轨道板的响应表现为随着温度的降低而增加的趋势,而在中高频段内则表现为随着温度的降低而减小的趋势.
可见,若忽略减振垫层的温频变特性,会对轨道板振动响应的预测产生比较大的偏差,因此为提高对轨道结构预测的准确性,有必要考虑减振垫层的温频变特性.
