一类整环中素元及唯一分解的研究

孙秀娟，祁 燕

（1.唐山师范学院 数学与计算科学学院，河北 唐山 063000；2.咸阳师范学院 数学与统计学院，陕西 咸阳 712000）

设w是固定的整数，那么

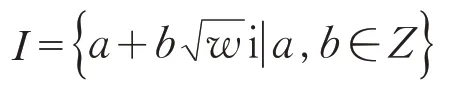
对于普通的数的加法和乘法作成整环。当w=-3，元素4 有两个不同的分解式

1 预备知识

定义1[5-7]整环I的一个元p叫作一个素元，假如p满足以下条件：

（Ⅰ）p不是零元；

（Ⅱ）p不是单位；

（Ⅲ）p只有平凡因子。

定义2[5]称一个整环I的一个元a在I里有唯一分解，假如满足以下条件：

（Ⅰ）a=p1p2…pr（pi是I的素元）。

（Ⅱ）若a=q1q2…qs（qi是I的素元），那么r=s，并且把qi的次序调换，使得qi=εi pi（εi是I的单位）（i=1,2,…,s）。如果I的既不是零元也不是单位的元都有唯一分解，称I是唯一分解环。

2 I中若干素元的确定以及整环I唯一分解的条件

在整环I中，ε是I的单位当且仅当 |ε|2=1。当w≥2 时，I的单位只有±1[8-9]。这一部分讨论I中既不是零元也不是单位的元是素元的充分条件。

定理1设α是非零整数，a,b,c,d∈Z,，则ad+bc=0,并且若b,d中有一个为0，那么另一个也为0。

证明：首先α=ac-bdw+，因为α是整数，所以ad+bc=0。若b=0，则ad=0。断言a≠0，d=0。反之，若a=0，则α=0，矛盾。同理可证，若d=0,则b=0，c≠0 。这就是说，若b、d中有一个为0，那么另一个也为0。

另外，设α∈I,a,b,c,d∈Z,

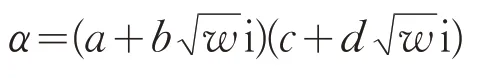
则取共轭，有

定理3设α是素数，α＜w,

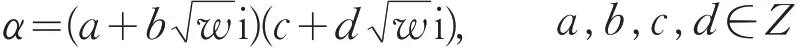
则α=ac,b=d=0，α是I中的素元。

证明：=α2=a2c2+a2d2w+b2c2w+b2d2w2。因为α2＜w2,所以b2d2=0。故b,d至少有一个为0。由定理1，b=d=0。这样，α=ac。因为α为Z中的素数，所以a或与α相伴，或a为单位。因此，α在I中无真因子，即α是I中的素元。

唯一分解环未必是主理想环，但是任何一个主理想环一定是唯一分解环[10]。下面讨论唯一分解环的充分条件。

例题1若w=2，则I是唯一分解环。

证明：设R是I的一个非零理想，令x是R中绝对值最小的非零元素，有(x)⊆R。下证R⊆(x)。

事实上，任取y∈R，那么

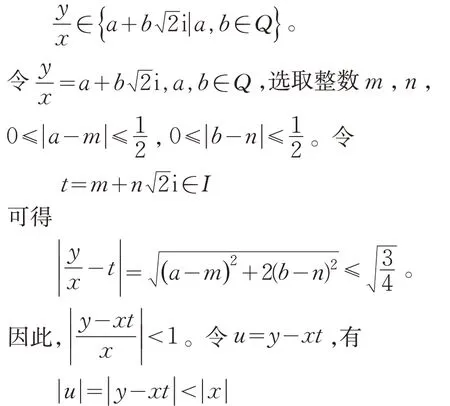
但x是R中绝对值最小的非零元素，所以u=y-xt=0。从而y=xt∈(x)，这样R=(x)，即I是主理想环，从而I是唯一分解环。

例题2当w=6，8，10，12，14，15，18，…，I不是唯一分解环。

证明：我们知道w=。对于大于等于6 的合数w而言，它至少可以分解成2 个素数的乘积，设w=n1n2…ni（nj是素数，j=1,2,…,i，i≥2）。由定理3 和定理4 知nj（j=1,2,…,i），为I中的素元。所以w在I中有两种不同的分解式，也就是说I不是唯一分解环。

例题3当w=3，5，7，11，13，17，19，…，I不是唯一分解环。

证明：若w是Z中的素数，令w=2k+1，则k+1 是小于w的整数，(k+1)2是合数，它至少可以分解成2个素数的乘积，不妨设为

3 结论

求整环中的素元没有一般的方法，本文通过对整环I中的元取共轭，结合素元的理论知识，求出了整环I中的若干素元：k±、小于w的素数和。通过例题的讨论，文中还给出了I为唯一分解环的充分条件是w=2。