针肋结构微通道热沉的结构优化设计

段治健，李 鑫，马欣荣

(1.咸阳师范学院 数学与统计学院，陕西 咸阳 712000；2.西北工业大学 航海学院，陕西 西安 710072）

微电子芯片、电池和模具等发热量较高的产品及装备对工作环境温度要求十分苛刻[1-3]。过高的温度会降低装置的工作效率和寿命，严重时直接导致设备损坏，引起火灾甚至人员伤亡。为了降低过热导致的危害，内置冷却通道的散热结构被广泛应用于雷达、汽车、轮船、潜艇、火箭和卫星等设备中[4-6]。

结构优化设计技术以数学优化方法为基础，通过改变工程结构的尺寸、形状或结构构型，在满足给定的约束条件下，能够实现最优性能的新型结构概念设计。特别是3D打印技术革命性的进展，使得结构优化设计技术可以应用于新型生物结构、微纳米结构、电磁超材料等诸多科学前沿领域。

自Bendsøe 和Kikuchi[7]开创性地将拓扑优化方法应用于结构设计以来，该方法逐渐被应用于流动问题、传热问题以及耦合问题。Saravanan 等[8]研究了针肋的半径、高度、间隔距离、雷诺数等参数对气冷通道热沉传热的影响，并利用结构优化方法得到了最优构型。Sui等[9]对波浪形通道针对不同雷诺数分析了传热系数、摩擦因数的影响。Guest[10]结合Darcy 与Stokes 方程设计了流动拓扑优化方法。文献[11-14]以多目标函数设计了对流传热拓扑优化模型，进一步扩展了拓扑优化的设计思路。

为了满足微通道热沉散热需求，本文研究了包含针肋结构的微通道热沉拓扑优化设计策略。

1 计算模型

1.1 几何结构

微通道热沉几何模型如图1（a）所示，结构尺寸为长（L）×宽（W）×高（H）=10 mm×10 mm×2.0 mm。加热底面厚度为Hb=0.5 mm，顶盖厚度为Ht=0.5 mm。图1（b）为包含4 个针肋结构的单个微通道几何模型：微通道尺寸为L×Wm×Hm=10 mm×0.5 mm×1.0 mm，针肋尺寸为高（Hp）×直径（D）=0.6 mm×0.3 mm，针肋等距分布，间距为d=1.3 mm。计算结构双外侧固体壁厚为0.25 mm。

图1 针肋结构微通道热沉几何模型

1.2 数值方法

微通道热沉的对流传热耦合问题满足质量、动量与能量守恒方程。采用非结构网格划分计算区域，结合间断Galerkin 有限元方法[15]求解偏微分方程组。

边界条件设置如图2 所示，初始温度T0=293.15 K，入口压力Pin=2 Pa，入口温度Tin=293.15 K，出口压力Pout=0 Pa。流固交界面采用壁面无滑移边界条件，针肋结构设定为多孔介质，初始材料体积占比为0.65。加热面给定恒定热流密度q=100 W/cm2，忽略流体物性变化，耦合对流传热计算微通道的综合性能。

图2 微通道热沉边界条件设置

流体材料属性：密度ρf=998 kg/m3，比热容Cpf=4 182 J/（kg·K），导热系数kf=0.6 W/（m·K），动力黏度μ=8.55×10-4Pa·s；固体材料属性：密度ρs=2 710 kg/m3，比热容Cps=902 J/（kg·K），导热系数ks=236 W/（m·K）。

对离散方程组采用高效隐式广义极小残余算法（Generalized Minimal Residual，GMRES）[16-17]，结合多重网格方法提高计算效率。

1.3 综合传热性能参数定义

流动雷诺数定义为

其中ρ为流体密度，u为入口流速，Dh为微通道的水力直径，μ为流体动力黏度。

由于针肋结构会增加流动损失，因此文中采用f/f0表征微通道的流动损失，引入范宁摩擦系数f为

其中Δp为压降，L为微通道长度。f0为光滑微通道的范宁摩擦系数，f0=0.046Re-0.2[18]。

为了表征微通道换热效率，定义微通道努赛尔数Nu为

其中q为加热面热流密度，Tw为壁面温度，Tf为流体温度；kf为流体导热系数。

引入针肋结构不可避免地会引起流动阻力增加，因此为了对强化换热进行综合评价，定义综合传热因子[18]

其中Nu0为光滑微通道的努赛尔数，综合传热因子η的值越大，则传热性能越好。

2 拓扑优化算法

流动传热优化问题的一般数学模型描述如下：

最小化/最大化：G(γ,u(γ))

满足：

其中G为目标函数，γ为设计变量（材料密度分布值），gi为等式约束，hj为不等式约束。

在整个设计区域中，根据γ的数值确定区域中材料的分布，函数g1，g2，…，gn为整个区域上的至少二阶可微的连续实值函数。对于不等式约束中的函数h1，h2，…，hm可以根据物理定律采用不同的表现形式，更好地描述拓扑优化系统的实际工况。此外，拓扑优化问题目标函数可以实现多目标函数优化。

2.1 优化数学模型

将计算区域划分为多孔介质、流体以及固体区域，引入Brinkman 惩罚项αu，则稳态不可压缩Navier-Stokes方程为：

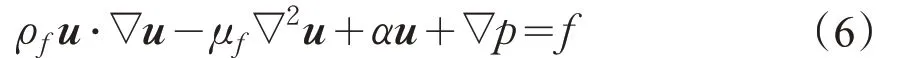
在流体区域上α=αf=0，惩罚项αu趋于零；在固体区域，迫使速度u趋于零。

热输运方程为

其中热传导系数k满足

采用材料属性的有理近似插值方法（Rational Approximation of Material Properties，RAMP）[8]定义多孔材料的物理属性，满足

其中αsf、ρsf、ksf、Cpsf分别为多孔材料的惩罚系数、密度、导热系数以及比热容。

结合边界条件，可得针肋结构微通道热沉的拓扑优化数学模型为

最小化：G=∫ΩTΩ·uΩ·ndA

满足：

其中γk为材料分布值，V=65%为材料体积约束上限，下标“s”代表固体，“f”代表流体。

2.2 优化算法

针对上述优化数学模型采用全局收敛移动渐近线方法求解[19]。方程（10）本质上属于0-1模型，求解时往往会出现棋盘格等现象，因此采用密度过滤与投影算法[20]克服数值不稳定问题，定义为

3 结果与分析

3.1 网格独立性验证

非结构网格具有良好的结构适应性，适合有限元方法求解，因此，针对微通道热沉几何结构采用非结构网格划分区域。为了验证网格独立性，文中采用三种网格，分别为：Case1（71.6 万），Case2（81.5万）、Case3（90.8 万）。图3（a）为微通道整体计算网格，图3（b）为针肋结构局部网格示意图。图4 给出了不同雷诺数Re下三套网格对应的最高温度的计算结果，可以看出Case1与Case2对应的最高温度最大误差与平均误差分别为1.80%、1.70%；Case2 与Case3 对应的最高温度最大误差与平均误差分别为0.15%、0.136%。显然，Case2与Case3的计算结果基本一致。因此，考虑到计算效率与计算精度，文中采用81.5万网格进行数值仿真。

图3 微通道换热器计算网格

图4 不同计算网格的最高温度分布

3.2 流动分析

图5 给出了光滑通道、针肋通道以及优化结构通道的沿程切面速度分布。显然，光滑平直微通道流速变化较小，而包含针肋结构以及拓扑优化结构的通道阻力增大，导致压降增加，在针肋结构处，通道面积减小，速度明显提升，尤其是拓扑结构速度梯度变化明显，从而引起边界层重启，使得冷却流体掺混效果增加，进而能更好地交换能量。图6给出了雷诺数为389.9 时，优化结构通道在高度方向z=0.3、0.5、0.7 mm 截面处的速度分布。可以看出，优化结构在针肋位置处的流速变化明显，随着高度增加，速度逐渐增加，优化设计增加了流固交界面的流动扰动；在拓扑结构分布区域，沿程流体速度逐渐减小，增加了冷却流体的停留时间，从而更好地降低微通道温度。

图5 沿程切向切面速度分布

图6 沿高度方向优化结构的不同截面速度对比

3.3 综合传热性能分析

图7 给出了在材料体积约束V=0.65 时，不同优化迭代步数对应的针肋截面材料分布（黑色为流体，白色为固体）。可以看出，当n从0 步迭代至20 步时，材料分布快速变化，随着迭代步数从20 步迭代至最终收敛，针肋结构的拓扑优化结构形状基本保持不变。优化结构上下边界的波纹形状逐渐清晰，在流固交界面上引起流体波动，能更好地交换能量，进而增强传热效果。

图7 不同迭代步的拓扑结构截面材料分布

图8给出了微通道的综合传热因子随雷诺数Re的变化规律。可以看出，随着Re的增加，优化结构对流体的掺混效果逐渐减弱，因此综合传热因子逐渐减小。在雷诺数Re=194.9 时，η增加了19.6%；在Re=389.9 时，η增加了13.4%；在Re=584.8 时，η增加了7.0%。平均传热效率提升了13.32%。相对于标准针肋结构，优化结构的平均综合传热因子增加了12.30%。显然，优化结构具有更好的综合传热性能。

图8 综合传热因子η随雷诺数Re的变化规律

4 结论

为了提高微通道热沉的散热性能，针对3D几何模型，研究了针肋结构微通道热沉的结构优化设计方案。基于RAMP方法，提出了拓扑优化数学模型，分析了拓扑结构的流动特性与综合传热特性，得到了以下结论：（1）采用RAMP方法，定义了多孔材料的物理属性，并将Brinkman 惩罚项引入Navier-Stokes 方程中，建立了针肋结构微通道热沉的拓扑优化模型；（2）采用GCMMA 计算了优化数学模型，分析了优化结构的流场与综合传热因子的变化规律。优化结构的底面温度分布更加均匀，平均综合传热效率提高了13.32%。