乌鲁木齐地铁隧道互层岩体力学特性及几何特征因子敏感性模拟*

谢良甫 王 博 王辉明 路玉佳

(新疆大学建筑工程学院，乌鲁木齐 830047，中国)

0 引 言

实际工程中，软硬互层状岩体广泛存在于隧道、边坡、地下洞室等领域，容易造成滑坡失稳(汤明高等，2019)、隧道塌方(Hsu et al.，2004)等复杂工程问题，因此众多学者在各个领域均展开了互层岩体力学特性研究(袁广祥等，2009；董雪等，2013；吉世祖等，2014；肖尚德等，2016；王飞等，2017；周云涛等，2017)。软硬互层岩体与均质岩体破坏特征差异显著(侯志强等，2019)，前者破坏过程更为复杂，破坏先兆信息更难预测(Yuan et al.，2016)、软层引起围岩的稳定性较低(范留明等，2006)、强度中等、耐久及耐磨损性较高(Yang et al.，2011)等特点。影响互层岩体破坏强度的主要几何特征因素包括：岩层倾角(王志杰等，2019a)，层厚(李昂等，2018)，层厚比(王志杰等，2019b)等。学者们大都通过数值模拟或室内试验的方式对软硬互层岩体的力学特性进行了研究。王志杰等(2019b)通过现场实验和数值模拟，分析不同层厚比对互层岩体稳定性的影响，认为层厚比在1︰1时，岩体稳定性最佳。吴渤等(2105)对互层岩体进行了室内试验和数值模拟分析，认为随着互层岩体岩层倾角的增加单轴抗压强度曲线大致呈U型变化趋势，并对不同倾角下的破坏模式进行总结与分类分析。李昂等(2014)基于FLAC模拟了互层岩体单轴压缩过程，认为岩层倾角与岩体内应力分布密切相关，在破坏过程中拉伸裂纹最先出现，随着剪切带的形成，裂纹扩展终止。邓荣贵等(2011)通过实验模拟了不同节理的层状岩石，并分析了力学及变形特性，认为当最大主应力与节理方向的夹角为0°、75°、90°时，对层状岩石的破坏特性影响较小，多条节理或其他夹角对层状岩石的破坏特性影响较大。虽然互层岩体力学特性研究成果众多，但大都是从岩层倾角变化的角度进行研究，对于影响因素作用下，互层岩体力学参数变化规律及裂纹等细观层面展开深入分析的研究较少，对于几何特征因子与互层岩体力学敏感性的分析更少。

随着乌鲁木齐轨道交通的发展，隧道穿越区域内大量的泥岩、砂岩组成的软硬互层岩体分布较广，因其力学性质复杂，容易造成的地表沉降、隧道塌方等工程稳定性问题尚未解决，以及目前关于乌鲁木齐地铁隧道软硬互层岩体力学特性的影响因素分析不够全面。基于此，为完善互层岩体力学特性理论，揭示其破坏机制。本文依托乌鲁木齐市地铁隧道，选取强风化砂岩、泥岩组成的软硬互层岩体为研究对象，采用颗粒流数值模拟单轴压缩试验从细观角度深入分析在岩层倾角、层厚比、层厚等因子作用下互层岩体的力学特性，依据正交试验法分析各因子敏感性，从而找到最有利组合及最不利组合。研究成果对互层岩体稳定性评价与预测具有一定的理论指导意义。

1 隧道地层特性及室内试验方案

1.1 隧道地层特性

乌鲁木齐地铁隧道一号线区间地质剖面如图1所示，隧道穿越区有大量的互层岩体存在。冲积、洪积河床堆积形成的第四系上更新统地层包括：圆砾、卵石，地表广泛分布杂填土，下伏侏罗系喀剌扎组上统岩层包括：泥岩、砂岩，两者呈互层状分布，层厚分布较为复杂(强风化泥岩夹强风化砂岩层、强风化砂岩夹强风化泥岩层等)，节理裂隙较为发育。强风化泥岩浅黄色，层状构造，泥质胶结，呈碎块状，局部有短柱状，属极软岩，层厚：2.8～12.8m，岩层产状：N45°E/20°～40°N。强风化砂岩，红褐色-灰黄色，细粒结构，局部为中粒结构，泥钙质胶结，厚层状构造，填充物为粉黏粒和褐铁矿，属极软岩，层厚：1.0～5.5m，岩层产状：N60°～65°E/25°N。

1.2 室内试验方案

乌鲁木齐1号线地铁隧道开挖后，在隧道穿越区大量的强风化泥岩、砂岩存在处，通过钻孔、取样获取岩芯。同时考虑到开挖面附近岩体扰动较大，其未被采用。取回的试样严格按照岩石力学试验要求进一步加工成高度10cm，直径5cm的圆柱体试样。试样在岩石三轴仪上进行伺服加压，加载仪器及试验过程如图2所示，加载速率为1.0kpa·s-1试样破坏后，实验数据被仪器自动记录，应力-应变曲线如图3所示，试验后经整理所得参数如表1所示。

表1 强风化泥岩、砂岩室内试验参数Table 1 Laboratory parameters of strong weathered mudstone and sandstone

2 颗粒流计算原理与数值试验方案

2.1 颗粒流计算原理

颗粒流模型是由不可破碎的圆形颗粒组成，采用牛顿第二定律从本质上描述颗粒间的复杂力学行为，把力学问题转化为数学问题，颗粒通过接触间的本构关系进行连接(Cundall et al.，1979)。本文使用线性平行黏结模型，平行黏结发生在两颗粒所受的微弱接触产生的挤压重叠处所形成的圆形或方形的有限范围内。平行黏结可以看作颗粒之间的重叠区有一组可以传递法向和切向力的弹簧，当接触间的力与力矩小于或等于0时，线性平行黏结本构关系存在，反之平行黏结接触被破坏，材料出现裂纹(Cho et al.，2007)。这种接触可以模拟颗粒间的弹性关系，因此比较适合岩体材料。

在颗粒流模拟单轴压缩试验时，数值模拟软件自带的编程语言提前设定好上下加压板的速度，并使上下加压板同时移动，利用数值软件内嵌的fish语言记录荷载作用下上下加压板所有垂直力并求和，然后除以试样的初始宽度(三维是体积或面积)得到轴向应力σ(Itasca et al.，2016)，记录上下加压板竖向位移，除以初始高度，得到轴向应变ε(Itasca et al.，2016)，σ、ε表达式如下。

(1)

式中：σ为应力；v为试样体积；Nc为测量区域接触的数量；Fe为颗粒间的接触矢量；Le为连接两个物体质心的分支向量；⊗为外积。

(2)

式中：ε为轴向应变；l为试样当前高度；l0为试样初始高度。

2.2 边界条件

在颗粒流数值模拟过程中，对试验施加荷载的过程主要分为两步。首先，生成由4块墙体组成的矩形区域，墙体被固定于相应的坐标，在矩形区域内生成颗粒并不断迭代达到相应的平衡。然后，左右两侧墙体被删除，左右两侧边界为自由边界。给颗粒赋予本构关系，岩体形成。上下墙体施加固定的移动速度，模拟轴向压力的施加，直至试样达到试验要求停止加压条件(当前试样所受轴向应力为峰值轴向应力的百分之七十时，试样停止加压)，试验模拟结束。

2.3 数值试验方案确定

本文选取了12cm×6cm的矩形模型模拟软硬互层岩体，考虑了层厚、层厚比(强风化泥岩与强风化砂岩之比，下同)、岩层倾角3个因素，每个因素分别考虑了5、13、9种情况，进行单轴压缩试验，具体试验方案如表2所示。

表2 试验方案Table 2 Test plan

3 数值试验模型建立及参数确定

3.1 数值试验模型建立

通过室内试验得到强风化泥岩、砂岩的物理参数，在此基础上进行微观参数标定，获取模拟互层岩体所需细观参数(表3)，使数值模型结果能够较为准确地反映实际工程中软硬互层岩体的力学特性。通过墙体生成命令，创建12cm×6cm的矩形模型模拟软硬互层岩体，使用ball distribute共生成6072个不同粒径的颗粒，在孔隙率为0.01作用下，采用时间步进行迭代，使初始状态的模型快速达到平衡。然后，删掉左右墙体，赋予平行黏结参数，用contact group对不同岩层赋予不同的力学参数。同时上下墙体会按照预设好的速度给试样加压，通过history命令监测，应力-应变等信息。如图4为试验中模拟的部分互层围岩试样，图4a为层厚比1、层厚为2cm、岩体倾角为0°的试样，图4b为层厚比1、层厚为2cm、岩体倾角为50°的试样。

表3 颗粒流数值模拟互层岩体所需细观参数Table 3 Meso-parameters required for particle flow numerical simulation of interbedded surrounding rocks

3.2 参数标定

为了使数值模拟得到的结果接近实际软硬互层岩体力学特性，首先采用单轴试验标定泊松比及弹性模量，然后采用双轴试验标定黏聚力和内摩擦角，在进行大量试验的参数调整后，标定应力-应变曲线(图5)，图5中室内试验的应力-应变曲线与数值模拟应力-应变大致相似，标定参数如表4所示，表4中试验参数与标定参数相差不超过15%。因此，数值模拟可以较好地反应实际岩体力学特性。

表4 宏细观参数与标定结果对比Table 4 Comparison of macroscopic and microscopic parameters with calibration results

4 单因素下互层岩体力学特征响应研究

4.1 岩体层厚

图6表示层厚比为1、岩层倾角为0°时不同层厚对单轴抗压强度的影响曲线。由图6可知，互层岩体抗压强度随着层厚的增加而降低，互层岩体层厚超过2cm时，单轴抗压强度的降幅相对于层厚为1.2～2.0cm时减小。在互层岩体为6.0cm 层厚时，单轴抗压强度最小，主要原因是随着岩体每层层厚的增加，较软的强风化泥岩快速地破坏，强风化砂岩未来得及破坏，试样整体就达到了模拟实验的停止加压条件造成的，降低了整个试样的承压能力。如图7为模拟试验中分析不同层厚岩体力学特性的部分试样图，图7a为层厚为6cm、层厚比为1、岩层倾角为0°的岩体试样，图7b为层厚为1.2cm、 层厚比为1、 岩层倾角为0°的岩体试样。

图8表示层厚比为1、岩层倾角为0°、层厚为3cm(图8a)、6cm(图8b)试样破坏后的裂纹图(图中红色为剪切裂纹，黑色为拉伸裂纹，下同)。图中强风化泥岩层出现大量的剪切裂纹及少量的拉伸裂纹，而强风化砂岩层几乎未出现裂纹。图9表示层厚比为1、岩层倾角为0°、层厚为：1.2cm、1.5cm、2cm、3cm、6cm条件下试样轴向应变与裂纹曲线图。

图9反映了层厚对裂纹的发展趋势及数量的影响关系，颗粒间的裂隙由于受到集中应力而产生裂纹，集中应力由剪切应力和拉伸应力组成，裂纹的发展就是集中应力不断释放给裂隙导致的。由图9可以看出随着互层岩体层厚的增加，裂纹数量呈下降的趋势，在层厚为1.5～2.0cm时，裂纹数量的变化较小，层厚对裂纹发展趋势大体相似。层厚1.2cm时试样破坏后在较小的应变范围内裂纹的数量直线增加，主要是试样内部结构完全被破坏，产生大量裂纹，表现出脆性破坏特征。层厚6cm相较于其他层厚裂纹数最少，裂纹发展最为迅速。可见层厚的不同对裂纹发展的数量及趋势都有明显影响。对比图6、图9可以得到层厚对单轴抗压强度与裂纹个数的影响基本呈现相同的减少趋势。图10表示层厚比为1、岩层倾角为0°、层厚为1.2cm的试样裂纹图，图中强风化泥岩层出现大量剪切裂纹及少部分拉伸裂纹，而强风化砂岩层出现较多的拉伸裂纹，及少量剪切裂纹。图11表示层厚比为1、岩层倾角为0°、层厚为1.2cm的应力、裂纹与应变的关系曲线图。

图10、图11可知，裂纹、应力-应变曲线总体分为5个阶段，OA段初始孔隙压密阶段：随着轴向应力的增加，颗粒间的孔隙率在减小，试样变得更加密实，应力-应变近似呈线性关系，裂隙受力较小，几乎未产生裂纹；AB段弹性应变阶段：应力-应变曲线近似为直线，此阶段的变形在荷载卸载后可以完全恢复；BC段裂纹稳定发展阶段：由于互层岩体每一层的强度不同，BC段中间出现多次应力峰值现象，主要是强风化泥岩强度较小，裂纹迅速发展(主要为剪切裂纹)，试样局部到达破裂，应力重分布导致的，同时会有少量拉伸裂纹出现；CD段裂纹不稳定发展阶段：试样内部有新的裂纹出现，裂纹、应力-应变曲线发展较为稳定，集中应力持续对裂隙释放，裂纹产生速度较上一阶段减缓，在其他薄弱部位仍然不断发生破坏，轴向应变发展较大，试样体积也在增加，试样达到极限承载能力；D点之后，由于之前已经多次出现强风化砂岩层的破坏，强风化泥岩也有较为明显的拉伸裂缝，试样承载能力迅速下降，而裂纹却迅速增加，出现裂纹交叉、相互贯通导致试样出现宏观断裂而破坏。

4.2 不同层厚比

图12表示层厚为2cm、岩层倾角为0°时、不同层厚比与单轴抗压强度的影响曲线图。由图12可知，互层岩体单轴抗压强度随层厚比的增加而减小。层厚比为0.1～0.6之间，随着强风化泥岩数量的增加，单轴抗压强度下降明显。层厚比为0.7～8之间，单轴抗压强度相对来说下降幅度特别小。在层厚比为8时单轴抗压强度达到最低。主要是随着层厚比的增加强风化泥岩在承受压力方面越来越起主导作用，强风化泥岩的单轴抗压强度相对于强风化砂岩较低，降低了试样的整体承压能力。

图13表示层厚为2cm、岩层倾角为0°、层厚比分布为0.1(图13a)、4(图13b)的试样裂纹破坏图，图13a强风化砂岩层出现了贯穿的拉伸裂纹，强风化泥岩层剪切裂纹较多，图13b强风化泥岩层有大量的剪切裂纹，少量的拉伸裂纹，强风化砂岩区几乎没有裂纹。造成这两种差异主要是不同岩层倾角的强风化砂岩承担轴向压力的比例不同。图14表示层厚为2cm、岩层倾角为0°、 不同层厚比下轴向应变与裂纹关系曲线图。

如图14，互层岩体所产生的裂纹数量随着层厚比的增加出现跳跃式的增减。总体来看，层厚比为0.1～0.6裂纹发展相对其他层厚比较为缓慢，而层厚比大于0.6时裂纹发展速度相对较快。主要是由于层厚比比较大时，强度相对较小的强风化泥岩占比增加，更多地承担了轴向应力，使裂纹的产生速度加快，试样的变形加大，强风化砂岩还未来得及产生更多裂纹和变形，就达到了数值模拟试验停止加压条件造成的。

图15为层厚比为0.4、岩层倾角为0°、层厚为2cm的试样裂纹破坏图，图中强风化泥岩层充斥着大量剪切裂纹，强风化砂岩层有少量的拉伸裂纹形成的裂缝。图16为层厚比为0.4、岩层倾角为0°、层厚为2cm的应力、裂纹与应变的关系曲线图。

图15、图16可知，OA段初始孔隙压密阶段、AB段弹性应变阶段两个阶段与图8中前两阶段比较相似，应力-应变近似呈直线关系，且几乎未产生裂纹；BC段裂纹稳定发展阶段：裂纹的产生较为迅速，应力-应变曲线出现较多小的峰值波动，主要原因是强风化泥岩占比较小，更容易在前期阶段出现多次薄弱部位的破坏，导致应力重分布，但是局部的破坏并不足以使整个试样停止加压的破坏条件；CD裂纹不稳定发展阶段：裂纹发展较为缓慢，同时拉伸裂纹也在不断发展，应力-应变曲线出现少量的拐点，说明这一阶段依然存在一定的应力重分布；D点之后，应力迅速下降，裂纹数量迅速上升，试样达到极限荷载，产生宏观裂纹而破坏。

4.3 互层岩体倾角

图17为层厚比为1、层厚为2cm时不同岩层倾角与单轴抗压强度的关系曲线图，由图17可知在岩层倾角为80°～90°时，单轴抗压强度有较大的变化。因此，为了探究其变化规律，从80°～90°之间取值观察单轴抗压强度的变化如图18所示，岩层倾角与单轴抗压强度近似呈线性关系增加。

图17分析了岩层倾角对单轴抗压强度的影响趋势，图形整体呈U形。这跟(吴渤等，2015)研究的随着互层岩体倾角的增大其单轴抗压强度曲线呈U形的结论基本相似。在0°～10°、40°～50°、以及70°～90°互层岩体的单轴抗压强度出现了较大变化，在10°～30°之间单轴抗压强度曲线较为平稳，40°左右时互层岩体的抗压强度达到最小。岩层倾角对单轴抗压强度的影响主要是因为强风化泥岩层出现剪切裂缝的方向与岩体倾角的方向越比较接近时，裂缝之间较易因压力的增加产生滑动，以及两种不同材料形成的交界面随着倾角的变化，承受剪应力的能力也有不同，使得试样承受压力的能力出现变化。

图19为层厚比为1、层厚为2cm、岩层倾角为20°(图19a)、70°(图19b)的试样破坏裂纹图，图19a的裂纹比图19b裂纹密一些，主要是图19b倾角较大，层间移动承担了一部分应力。图20为层厚比为1、层厚为2cm、 不同岩层倾角下轴向应变与裂纹的关系影响曲线。

图20裂纹数量及裂纹随应变的发展趋势也有较大差异。岩层倾角为40°时裂纹数量较少，裂纹发展趋势最快，岩层倾角为90°时的裂纹相较于其他岩层倾角数量最多、 发展趋势最为缓慢。由此可见，岩层倾角的改变，使得剪切裂纹方向与岩层倾角夹角产生不同程度的减小，从而使得10°到80°的裂纹数量较少且裂纹发展较为迅速。

图21为层厚比为1、岩层倾角为70°、层厚为2cm的试样裂纹破坏图，图中强风化泥岩层，出现大量剪切裂纹及少量拉伸裂纹，强风化砂岩层，几乎没有裂纹出现。图22为层厚比为1、岩层倾角为70°、层厚为2cm的应力、裂纹与应变的关系曲线图。

由图21、图22可知，OA段初始孔隙压密阶段，岩体孔隙在不断被压密；相对于图11、图16，AB段弹性应变阶段较长，即随着轴向荷载的增加，轴向应变在增加，但是却未产生裂纹，这主要是由层间滑动引起的变形；试样产生的变形基本为可恢复的弹性变形；BC段裂纹稳定发展阶段，此阶段产生的变形为塑性变形，裂纹增长速度较为缓慢；CD段裂纹不稳定发展阶段较短，裂纹迅速增加，这主要是层间滑动后，互层岩体本身迅速破坏所引起的裂纹增加，C点为小的拐点，互层岩体局部出现破坏，应力重分布；D点破坏之后应力随着应变的增加缓慢下降，裂纹-应变曲线急速上升，但应力并未降至0，说明试样还有一定的承载能力。

5 几何特征因素对互层岩体力学特征敏感性研究

5.1 正交试验设计及数值模拟结果

由第4节知，层厚比、层厚、岩层倾角3个因素单一作用下对互层岩体的单轴抗压强度及裂纹都有一定的影响，为了确定多因素对互层岩体作用下的最优组合(单轴抗压强度最大)与最不利组合，以及各因素对单轴抗压强度的敏感性，故采用正交试验进行分析。正交试验基于优化设计思想，在众多实验中找出代表性强的试验，通过对少数试验的分析，得到各因素对试验结果的影响因素，进而得到最有利及最不利组合。

正交试验的步骤为(倪恒等，2002)：(1)根据几何特征因素个数以及每个因素所要分析变化范围，选择合适的正交表，记为Ln(rm)，L表示正交表的标志，n为正交表的行数(即每个因素分析的次数)，r为因素水平数，m为正交表列数。(2)借助正交试验软件，使各因素在正交表中随机分布，得到计算方案。(3)严格按照计算方案通过模拟实验获取计算结果。(4)对正交表进行方差分析，并进一步解读分析结果。

本文在不影响各因素对互层岩体单轴抗压强度变化趋势的情况下，分别在每组选出4个水平(表5)，组成3因素4水平进行正交试验。表6为正交试验设计及数值模拟结果。

表5 试验因素与水平数Table 5 Test factors and levels

表6 正交试验设计及数值模拟结果Table 6 Orthogonal experiment design and numerical simulation results

5.2 正交试验结果分析

本次试验采用方差分析，方差分析可以精确分析出各因素对互层岩体单轴抗压强度的影响程度，并且能够区分试验本身引起的误差和改变水平数所引起的误差。正交试验本质是通过F检验统计量分析各因素对模拟指标影响的显著性，现对F(倪恒等，2002)检验统计量构造如下(倪恒等，2002)：

(3)

(4)

式(4)(倪恒等，2002)中：sT为总离差平方和，指总体样本值的离散状况；SA为组间误差平方和，指i列样本不同水平的差异程度，其自由度为(s-1)，记为hA；sE为组内误差平方和，指样本总体均值之间的差异，其自由度为(n-s)，记为hE。根据上述关系构造F为：

(5)

通过给定的显著水平α，依据Fj与F1-α(fA，fE)的关系判断该因素的显著性。

根据表4正交表可分别得出hA为3，hE为8，进一步通过式(4)到式(5)可计算出Fj值。选取显著水平α=0.01及α=0.05，通过F分位表，得F0.99(3，8)=7.59，F0.95(3，8)=4.07。当Fj大于F0.99(3，8)时认为几何特征因子对单轴抗压强度的影响非常显著，当Fj小于F0.99(3，8)大于F0.95(3，8)时认为几何特征因子对单轴抗压强度的影响显著，当Fj小于F0.95(3，8)时认为几何特征因子对单轴抗压强度的影响不显著。如表7为正交试验分析结果。

表7 正交试验Fj值分析结果Table 7 Fj-value analysis results of orthogonal test

根据表7可得层厚比对单轴抗压强度影响显著。层厚及岩层倾角对单轴抗压强度不显著，但Fj值不同，其值稍大的相对显著性强一些。因此，由表7可得，几何特征因素对单轴抗压强度敏感性由大到小依次为：层厚比、岩体倾角、层厚。

均值可判断正交试验中每个因素各水平对试验指标值的影响程度，均值越大该水平对试验结果越敏感，试验中单轴抗压强度越大越有利，因此由表8可选出多种组合如表9。

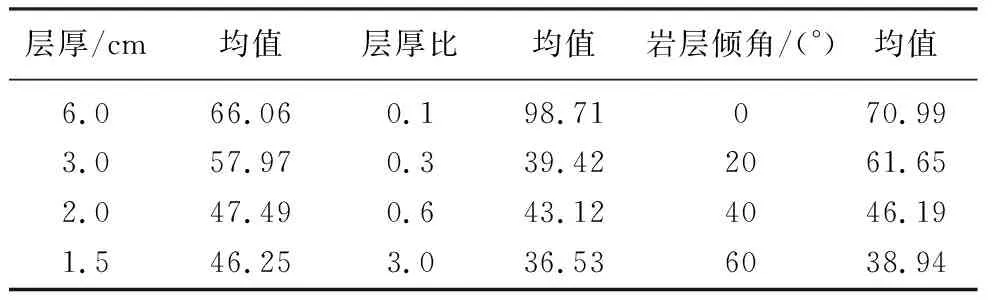
表8 正交试验均值分析结果Table 8 Mean analysis results of orthogonal test

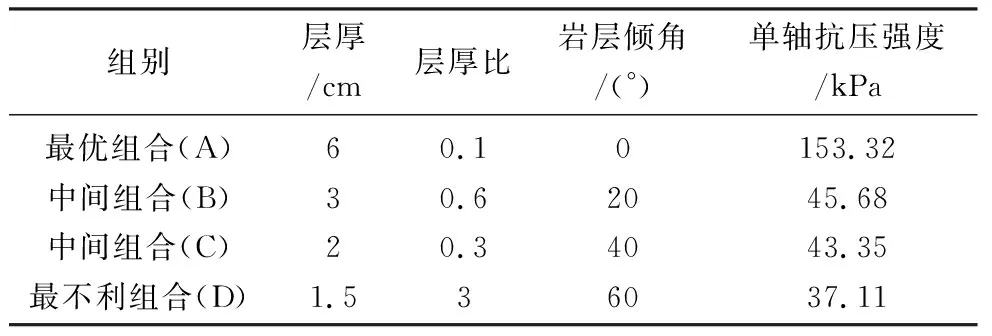
表9 不同均值下的组合Table 9 Combinations under different mean values

6 结 论

(1)互层岩体单轴抗压强度随着层厚比的增加而减小。在层厚比0.6～1附近减小趋势不明显。

(2)随着互层岩体岩层倾角的增加，试样的单轴抗压强度总体上呈U字形趋势变化，在岩体倾角为40°时达到最低。

(3)不同数值的层厚、层厚比、岩层倾角对裂纹数量及发展趋势都有较大的影响。层厚对裂纹影响较有规律，随着层厚的增加，裂纹数量减小，裂纹增加趋势加快。层厚比对裂纹的影响，从数量角度分析为跳跃性没有规律性，但从发展快慢趋势角度分析层厚比为0.1～0.6时发展较为缓慢，层厚比大于0.6时发展较为迅速。岩层倾角为0° 时裂纹较多，发展趋势较为缓慢，而在其他角度裂纹数量及发展趋势都比较相近。

(4)几何特征因素对单轴抗压强度敏感性由大到小依次为：层厚比、岩层倾角、层厚，并得出了最优组合。

本文使用了乌鲁木齐地铁隧道的实际互层岩体的力学参数，并在颗粒流软件中进行标定。能够比较准确地反映乌鲁木齐地铁隧道互层岩体实际情况的力学特性，希望能够对乌鲁木齐地铁建设中遇到的复杂岩体状况，提供一定的参考依据。