川南深层页岩水力压裂缝网扩展规律数值模拟研究*

2022-10-06孙景行刘俊辰黄浩勇姚志广岳文翰桂俊川徐尔斯张召彬赫建明

工程地质学报 2022年4期

关键词：压裂液主应力排量

孙景行曾波刘俊辰宋毅黄浩勇姚志广岳文翰桂俊川徐尔斯张召彬赫建明

(①中国矿业大学(北京)，力学与建筑工程学院，北京 100083，中国)

(②中国石油西南油气田分公司页岩气研究院，成都 610051，中国)

(③中国科学院地质与地球物理研究所，中国科学院页岩气与地质工程重点实验室，北京 100029，中国)

0 引言

水力压裂工艺是页岩储层改造的常用方法，其将高压的压裂液注入到低渗致密页岩储层，利用产生的流体压力和渗流作用使井筒周围产生裂缝并扩展，进行压裂改造释放页岩气(高强等，2020；冯雪磊等，2021)。我国川南地区页岩气资源丰富，其中志留系龙马溪组富有机质页岩厚度大、品质最优，是目前我国主力页岩气勘探开发层系(马新华等，2018)。目前3500m以深页岩气资源量占整个川南地区总资源量的比例高达86.5%(董大忠等，2012)，部分储层埋深已经接近5000m的深度范畴，这些深埋页岩储层的开发与3500m以浅区相比具有构造复杂、地应力差异大等特性，导致压裂形成复杂缝网的难度大，对于储层改造工程形成了巨大挑战(曾波等，2022)。因此有必要通过数值模拟研究深层页岩气水力压裂复杂缝网的主控因素，对实现川南地区深层页岩气的效益开发具有重要意义。

对水力压裂的过程进行数值模拟可以高效地研究压裂过程中各参数对压裂效果的影响，从而对现场施工提供指导。常用的裂缝扩展数值模拟方法包括有限元法、扩展有限元法、离散元法以及边界元法等(张搏等，2015)，本次研究压裂过程的数值模拟采用的位移间断边界元法在1976年被Crouch等人提出(Crouch，1976)，Olson(1993)将其应用到了水力压裂领域，并引入三维修正系数来计算单条缝高固定的水力裂缝的应力场(Olson，2004)。Olson et al.(2009)使用位移间断边界元法经过三维系数修正后分析了水平井分段多簇压裂中多裂缝同时扩展时的裂缝几何形态，并提出使用净压力系数来判断水力裂缝在含有天然裂缝储层中形成的裂缝网络的复杂程度。有学者建立了水力裂缝诱导应力场的模型，讨论了裂缝属性、射孔、地应力对产生复杂缝网的影响，但只考虑了裂缝形成初期井筒附近水平应力的变化，并没有考虑水力裂缝与天然裂缝的相互作用(郭建春等，2014)。赵金洲等(2014)计算了裂缝之间的应力干扰并讨论了不同地层参数和施工工艺参数对裂缝形状的影响，但其数值模拟模型为随机设置，不能很好地反映现场实际工程条件。考虑应力干扰和天然裂缝的影响，曾青冬等(2015)研究了簇间距对不同裂缝进液量的影响及天然裂缝属性和地应力差对复杂缝网的影响，但没有将应力干扰和天然裂缝结合在一起进行分析，仅分开讨论了其影响。Zhang et al.(2015a，2015b)结合页岩样品设计了虚拟裂缝系统来模拟难识别的小裂缝，建立了流体-岩石耦合系统的数值模型，对最大主应力方向和裂缝形态之间的关系进行了研究并推导了一个无量纲数M来解释裂缝扩展的稳定性。有学者通过引入图论将天然裂缝网络和预期水力压裂网络映射成图并采用位移间断边界元法研究了水力裂缝网络受天然裂缝网络、地应力和压裂参数的影响(Cheng et al.，2017)。

近年来有关三维水力压裂数值模拟的研究引起了许多学者的重视。有学者在Olson建立的模型基础上，建立了多条水力裂缝在裂缝性储层中的扩展模型，用位移间断边界元法计算裂缝间的应力干扰，该模型具有计算速度快的优势，但是无法考虑储层中的非均质和各向异性(Weng et al.，2011；Kresse et al.，2013)。Wu et al.(2016)设计了一种更精确的计算三维断裂应力和位移的方法，模拟了单个压裂阶段内多个裂缝同时传播的情况并研究了射孔簇间距、应力差及天然裂缝的几何形状对注入压力和裂缝复杂性的影响。有学者基于位移间断边界元法建立全三维模型并分析了多条水力裂缝在不同地应力场中的同时传播，研究了地应力分布对裂缝几何形状和相互作用的重要性，并对射孔参数进行了优化，但忽略了天然裂缝对裂缝扩展的影响(Tang et al.，2019；Cheng et al.，2021)。

基于从川南页岩气气田某井区采取的岩芯经观察重构的真实裂缝模型，本文采用位移间断边界元法模拟深层页岩储层中水力裂缝与天然裂缝相互作用的物理力学过程，研究压裂缝网扩展形成的规律与主控因素。研究结果能够较好地反映场地实际压裂情况，为川南深层页岩气水力压裂设计和施工提供参考。

1 裂缝扩展计算原理

位移间断边界元法只对模型中的裂缝进行初始网格划分，沿着新形成的边界可以生成更多的单元用于裂缝扩展的计算，通过添加用于裂缝扩展建模的新单元来调整网格，该情况下裂缝可被当作位移间断，其根据每个裂缝单元的法向位移(w)和剪切位移(v)的组成进行量化。在压裂过程的建模中，裂缝张开和滑动引起的应力分量如式(1)和式(2)所示(Xi et al.，2013)。

(1)

G22(X，s)v(s)]K(X，s)ds

(2)

式中：X=(x，y)是裂缝单元的坐标；对于闭合的裂缝，法向应力和剪切应力的关系为|τs|≤λσn，对于被打开的裂缝，τs=0且σn=pf，pf为流体压力。

裂缝中流体的体积流量q和在一维流动中施加质量守恒的连续性方程见式(3)。

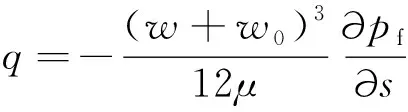
(3)

式中：q为裂缝中的流速；μ为流体动力黏度；w0为初始孔径；w为孔径；∂pf/∂s为流压梯度；vf为流体体积；L为裂缝段长度。

裂缝的扩展判定基于最大环向应力准则，其强度因子超过临界值时会发生扩展。水力裂缝遇到天然裂缝时会在天然裂缝的另一侧添加虚拟裂缝单元以检查应力状态。满足式(4)时，水力裂缝将穿过天然裂缝，其中，θ是裂缝扩展方向与当前裂缝方向的夹角，KIC为断裂韧度，KⅠ，KП为应力强度因子。

=KICKⅠsinθ+KП(3cosθ-1)=0

(4)

图1展示了采用DDM的计算步骤，最重要的过程是通过Gauss-Seidel迭代法求解流体压力pf、孔径w、滑移距离v、流体体积vf，随后检查裂缝是否发生扩展(Zhang et al.，2015a, 2015b)。裂缝扩展时，只需添加裂缝单元而无需对现有网格进行重新划分，DDM的重点是裂缝的传播和流体在裂缝空间中的流动。

2 计算结果及讨论

2.1 计算模型及参数

采用手持显微镜、体式显微镜为观察工具，对川南地区页岩气气田某井的岩芯进行了细观尺度下的观察和重构，各层位重构如图2所示，图中从左至右为埋深方向，从上至下为岩层方向。重构后对页岩储层的裂缝长度和密度进行统计分析，构建页岩岩芯二维裂缝模型(霍健等，2021)，最终建立的计算模型如图3所示。

图3为建立的二维裂缝计算模型，其中蓝色线条代表天然裂缝，红色十字代表压裂液注入点。模型尺寸为1m×1m，层厚设置为0.3m，裂缝网络密度为1.728m-1，整体密度偏差不超过0.3%，符合观察统计的裂缝长度及密度分布。模型边界为固定边界，最大主应力沿着竖向布置，其他模型材料参数如表1所示。该模型直观地展现了岩芯不同层位的裂缝分布，计算出的结果能够较好地反映场地实际。

表1 计算模型物理力学参数Table 1 Physico-mechanical parameters for calculation model

2.2 结果讨论与分析

图4 展示了不同主应力和排量条件下的压裂缝网及流体压力结果，未受影响的天然裂缝由深蓝色线条表示，可以看到模型注入点附近的流体压力最高，裂缝尖端的流体压力最低。裂缝扩展主要有两个传播方向，第1个是主天然裂缝方向(大致平行于x轴)，缝网主要通过激活天然裂缝沿该方向传播；第2个是最大主应力方向(沿y轴)，缝网主要通过产生新生裂缝沿该方向传播。工况(1)至工况（1）均为排量1L·min-1主应力差10MPa的工况，随着主应力增加，缝网内流体压力增加，缝网复杂程度降低；排量提升到2L·min-1后从工况(7)至工况(12)可以看到裂缝内流体压力提升较少，和1L·min-1工况相比，在高主应力下缝网复杂度提升的程度相较低主应力情况更加显著。

主应力差提高到20MPa之后从工况(13)至工况(18)可以看到缝网复杂度均显著降低，在最大主应力为135MPa时(工况(18))只生成一条水力裂缝，压裂效果差；提升排量到2L·min-1后从工况(19)至工况(24)同样看到在低主应力情况下裂缝内流体压力提升较少，缝网复杂程度提升不高，在最大主应力为115MPa和135MPa时(工况(23)和工况(24))相比低排量条件激活了更多的天然裂缝。

主应力差和主应力的大小直接影响着缝网形态的变化。当主应力较高时，裂缝扩展需要的能量较高，水力裂缝扩展能力较弱，缝网复杂度较低；当主应力差较高时，裂缝沿最大主应力方向扩展的趋势增强，难以在其他方向形成分支扩展，形成的缝网形态均较简单。

2.2.1 裂缝平均宽度变化

图5展示了不同工况下压裂缝网平均宽度的变化情况。在主应力差为10MPa时裂缝平均宽度随主应力的增加而增大，增加幅度为11%，主应力差为20MPa时裂缝平均宽度均随主应力的增加而增大，增加幅度为24%，说明主应力增加会导致地层中的破裂压力增大，裂缝平均宽度增大，当主应力差较高时裂缝平均宽度随主应力增加而增大的幅度更显著。

主应力差为10MPa时，增加压裂液排量导致缝网平均宽度平均增加9%；主应力差为20MPa时，压裂液排量提升导致缝网平均宽度平均增加3%，说明在较高主应力差条件下压裂液排量增加而导致压裂缝网平均宽度增大的能力变得有限。压裂液排量为1L·min-1时，主应力差增大10MPa导致缝网平均宽度平均增加17%，压裂液排量为2L·min-1时，主应力差增大10MPa导致缝网平均宽度平均增加11%，说明提升排量会导致地层中的破裂压力增大，裂缝的平均宽度增大，但是排量提升会使主应力差增大导致缝网平均宽度的增大的能力变得有限。

2.2.2 裂缝总长度变化

图6展示了不同工况下压裂缝网中新生裂缝、天然裂缝和缝网总长度的变化情况。可以看出主应力和主应力差对裂缝长度的影响十分明显。主应力差不变时随着主应力的增加，模型中产生的新生裂缝和激活的天然裂缝长度均降低，但各自所占缝网总长度的比例变化有所不同。其中主应力差为10MPa，排量为1L·min-1时随着主应力的增加，天然裂缝所占比例为45%～17%，新生裂缝所占比例为54%～82%；排量提高到2L·min-1后天然裂缝所占比例为45%～35%，新生裂缝所占比例为54%～64%。主应力差提升到20MPa后，随着主应力的增加，裂缝所占比例变化不明显，其中排量为 1L·min-1时天然裂缝所占比例平均值为24%，新生裂缝所占比例平均值为76%；排量提高到2L·min-1后天然裂缝所占比例平均值为27%，新生裂缝所占比例平均值为73%。

在主应力差为10MPa时，小排量下压裂液激活天然裂缝的能力受主应力的影响更明显，在较高的主应力下排量提升1L·min-1激活的天然裂缝长度提升近一倍，但同时新生裂缝长度变化不明显。主应力差提高到20MPa后，压裂液激活天然裂缝的长度相比与主应力差为10MPa的情况，降低幅度十分显著，同时排量提升后产生新生裂缝的长度有所提升，但并不能显著增加压裂液激活天然裂缝的长度。可见主应力差为10MPa时提高压裂液排量，缝网长度的增加以激活天然裂缝为主，主应力差为20MPa时提高压裂液排量，缝网长度的增加以产生新生裂缝为主。

图4可以看出在小排量、主应力差不高的条件下水力裂缝会优先向存在天然裂缝的位置扩展，主应力差为10MPa时，随着主应力的增大，裂缝扩展路径复杂度降低，沿着最大主应力方向扩展的趋势增强，裂缝长度的变化较为明显。主应力差为20MPa，排量为1Lmin·-1时主裂缝沿着最大主应力方向扩展的趋势增强，难以在其他方向形成分支扩展，当主水力裂缝前缘接近天然裂缝时直接穿过天然裂缝的情况更多，导致了水力裂缝中以新生裂缝为主；排量增加到2L·min-1后并没有激活较多的天然裂缝，裂缝基本还是沿最大主应力方向扩展，沿天然裂缝扩展的裂缝也在扩展较短距离后向最大主应力方向发生转折，所以在高主应力差的条件下提升压裂液排量对激活天然裂缝、形成复杂缝网具有一定作用，但效果一般。

图7展示了不同工况下压裂缝网的总长度。可以看到主应力差的变化对缝网长度影响十分显著，压裂液排量为1L·min-1时，主应力差提升10MPa导致缝网总长度平均降低70%，压裂液排量提升到2Lmin·-1时，主应力差提升10MPa导致缝网总长度平均降低63%，可见主应力差提高会导致缝网总长度明显降低。从图4的工况(13)至工况(24)可以看到主应力差提高会使水力裂缝扩展时沿各个方向产生新生裂缝的数量降低，压裂液激活的天然裂缝数量明显减少，缝网复杂程度显著降低，从而降低缝网的总长度。

主应力差为20MPa时，压裂液排量从1L·min-1提升至2L·min-1缝网总长度平均增加23%。主应力差为10MPa时，压裂液排量从1L·min-1提升至2L·min-1时除最大主应力为95MPa、115MPa两种工况反常外，其他工况中缝网总长度平均增加15%，说明排量增加，压裂液打开的裂缝增多，缝网长度增加。观察图4中(4)、(10)、(5)、(11)4种反常工况可发现工况(4)裂缝扩展途中与天然裂缝相遇时，发生了较多的分支扩展，缝网复杂程度较高，而工况(10)由于排量较大，水力裂缝下半部在扩展时直接穿过遇到的天然裂缝，到达模型边界导致计算停止，所以裂缝扩展时间更短，缝网长度偏低。同样工况(11)相比于工况(5)，压裂液排量更大，水力裂缝下半部分在扩展时直接穿过遇到的天然裂缝到达模型边界导致计算停止，裂缝扩展时间较短，缝网总长度偏低。说明主应力较高时，高排量相比于低排量，裂缝扩展时更可能直接穿过遇到的天然裂缝。

图8展示了不同工况下压裂缝网中拉张裂缝和剪切裂缝长度的变化情况。随着主应力增加，所有工况中压裂缝网的剪切裂缝长度明显降低，拉张裂缝长度基本保持不变。在主应力差为10MPa，排量为1L·min-1的情况中，随着主应力增加，剪切裂缝所占比例为89%～65%，剪切裂缝长度降低但仍然长于拉张裂缝；排量提高到2L·min-1后随着主应力增加，剪切裂缝所占比例为89%～77%，主应力差为10MPa时，提高排量导致剪切裂缝长度平均增加11%，拉张裂缝长度变化不明显。主应力差提高到20MPa后，排量为1L·min-1时随着主应力增加，剪切裂缝所占比例为64%～20%，拉张裂缝所占比例为36%～79%，可以看出在最大主应力增至75MPa时两种裂缝长度趋于相等，随后剪切裂缝长度开始低于拉张裂缝长度；排量提高到2L·min-1后随着主应力增加，剪切裂缝所占比例为65%～26%，拉张裂缝所占比例为35%～74%，主应力差为20MPa时，提高排量导致剪切裂缝长度平均增加32%，拉张裂缝长度平均增加10%。说明相比于拉张裂缝，剪切裂缝的形成受主应力和压裂液排量的影响更大，并且在较高主应力差条件下随着主应力增加，剪切裂缝长度的降低程度更加显著。

对于大多数天然裂缝，在被流体压力重新激活之前会发生剪切，剪切是由注入流体后裂缝表面之间的摩擦应力减小而造成的，而新形成的裂缝在后续扩展中又可能发生剪切，所以剪切裂缝的长度通常比拉张裂缝长，大部分剪切裂缝为天然裂缝，新形成的裂缝倾向为拉张裂缝。但是在图8红色方框显示的情况中，拉张裂缝比剪切裂缝长，这是因为在该情况下沿天然裂缝的剪切应力非常小，结合图4中工况(15)至工况(18)、工况(22)至工况(24)可以看到水力裂缝扩展时主要生成一条水力主裂缝，导致缝网以拉张裂缝为主，剪切裂缝为辅。

2.2.3 裂缝长度随压裂液注入变化

图9展示了不同工况下压裂裂缝长度随压裂液注入量的变化情况。在压裂初始阶段曲线斜率较大，注入一段时间后曲线斜率会有所减小，这是因为随着裂缝扩展数量的增多，压裂液的动力效应减弱，水力裂缝扩展能力减弱，扩展速率降低。在主应力差为10MPa、压裂液注入量相同的条件下，排量为1L·min-1和2L·min-1的裂缝长度在压裂前期基本相同，但在压裂液注入一定量之后，排量1L·min-1中的裂缝扩展长度甚至大于排量2L·min-1中的裂缝扩展长度，结合图4中的工况(1)至工况(12)可见这是因为随着水力裂缝的扩展，排量为2L·min-1下的水力裂缝中水力能量较高，当裂缝尖端接近天然裂缝时，直接穿过天然裂缝而生成新生裂缝的情况更多，该情况消耗的能量更多，耗时更长，所以注入相同压裂液时裂缝长度更低。在主应力差为20MPa、压裂液注入量相同的条件下，不同排量下的裂缝长度差距不明显，结合图4中的工况(13)至工况(24)可见当主应力差较高时会使裂缝沿着最大主应力方向扩展的趋势增强，降低排量对于裂缝扩展形成复杂缝网的影响程度，说明当主应力差较高时提升压裂液排量对于提升裂缝的复杂程度十分有限。

从图9 还可以看出在压裂液排量相同时，在较高主应力差的条件下，裂缝扩展速率较小。主应力差较低时，主裂缝在扩展过程中更易激活天然裂缝，扩展速率更快。主应力差增大，主裂缝沿着最大主应力方向扩展的趋势增强，遇到天然裂缝时更可能直接穿过天然裂缝，扩展速率降低且越来越难以在其他方向形成分支扩展，压裂液的注入总量随着应力差的增大而下降。