基于分数阶导数理论的Q3黄土流变本构模型研究*

慕焕东 邓亚虹 赫 佳 李 丽

(①长安大学地质工程与测绘学院，西安 710054，中国)

(②矿山地质灾害成灾机理与防控重点实验室，西安 710054，中国)

(③甘肃省交通科学研究院有限公司，兰州 730050，中国)

0 引 言

黄土广泛分布于我国西北地区，其在荷载的长期作用下可能发生蠕变和渐进破坏等流变现象(如西安地铁开挖的黄土隧道以及岩土工程中常见的边坡、挡土墙、地基与路基渐进破坏)，进而影响工程建构筑物的长期稳定性。因此，分析黄土在长期荷载作用下的应力-应变关系进而建立考虑流变特性的黄土本构模型对黄土地区工程设计具有重要的理论与工程实际意义。

学者们对岩土材料流变特性及本构模型的研究多从元件蠕变模型和经验蠕变模型两方面考虑。经验蠕变模型研究较为广泛，如陈昌富等(2008，2019)将固结理论与Kelvin蠕变模型相结合，建立了考虑固结-蠕变耦合作用的蠕变模型可合理评价软土或红黏土蠕变特性。刘忠玉等(2019)引入考虑时间效应的统一硬化(UH)本构模型描述饱和黏土的黏弹塑性并与一维流变固结试验结果对比验证其有效性。苏白燕等(2015)对重庆武隆鸡尾山滑坡滑带(炭质泥质灰岩)进行了岩石饱水直接剪切流变试验，得出滑带炭质泥质灰岩的剪应力-剪切位移曲线及其长期强度。李佐良等(2013)对德州松软土进行不同围压下的三轴固结不排水蠕变试验，建立了其分数阶蠕变本构模型。

元件模型以Maxwell、Kelvin、Burgers最为经典。对于黄土来说，目前大多采用由基本元件模型组成的整数阶模型，林斌等(2010)基于不同含水量Q3黄土的蠕变特征分析，将一个Hooke体与多个Kelvin体串联，提出了黄土损伤与流变耦合作用的本构模型，该模型可以准确描述黄土的突发性破坏特征；王鹏程等(2014)对陕西省泾阳县原状黄土进行室内三轴固结排水蠕变试验，以此建立了黏弹塑性九元件蠕变模型，该模型通过1个K体和2个V/K体来描述原状黄土的线性流变特性，但该模型仅可以较好地描述该地区黄土的三轴线性蠕变特性，不具备说明问题的普遍性。与此同时，现有研究表明在实际中为了提高模型的预测精度，在整数阶流变本构模型中往往通过串联多个K体来实现，从而增加了模型的复杂程度及求解参数的难度。然而，由传统的线性流变元件串联或并联组合而成的本构模型只能描述黄土的减速与等速蠕变，无法反映加速蠕变阶段(孙均，1999)。

上述学者提出的蠕变模型虽具有很多优点，但对蠕变试验曲线中加速蠕变阶段不能全面、精准描述，现有的研究还不能形成合理而又统一的认识，是目前研究中所面临的根本问题。上述问题主要是考虑加速蠕变阶段的非线性特性，为此，越来越多的学者们展开对非线性元件本构模型的研究。众所周知，由于含水率的不同，土体的软硬状态不同，因此可以认为土体是一种介于理想固体与理想流体之间的材料。基于这样的前提，殷德顺等(2007)基于分数阶微积分原理，改造出介于理想固体与理想流体之间的软体元件，建立了改进的分数阶蠕变本构模型，与整数阶模型相比，该模型可以更好地描述土体的非线性流变特性。在分数阶流变本构模型研究方面，学者们考虑多种类型岩土材料，对其本构模型进行拓展得到了分数阶的蠕变本构模型，并通过室内试验验证了其有效性。涉及到的岩土材料主要包括软黏土、冻土、软土、泥岩、软岩、盐岩等(孙海忠等，2007；何利军等，2011；宋勇军等，2013；吴斐等，2014；闫云明等，2017；蒋秀姿等，2018；孙凯等，2018；倪静等，2019；孙萍萍等，2020)。上述对于分数阶蠕变本构模型的研究具有非常重要的理论意义，但目前的研究对黄土材料研究较少，而黄土材料广泛分布于我国西北地区，承载的工程建构筑物极其广泛，同时已有研究表明在荷载的长期作用下，黄土所表现出的非线性蠕变特性成为影响其安全的重要因素，尤其是其蠕变变形和长期强度，往往是致使建构筑物变形失稳亦或强度破坏的主导因素之一。

关于黄土流变特性的研究，本课题组已通过三轴循环加卸载蠕变试验，基于统一流变力学模型理论，建立了由西原体与村山体串联组合而成的改进西原模型(李丽，2013；邓亚虹等，2015；李飞霞，2016；李丽等，2017，2018)。该模型能较好地描述Q3黄土的减速蠕变与等速蠕变阶段，但对于黄土流变试验曲线段(减速与加速蠕变段)无法准确描述，尤其是对不同于改进西原模型线性元件的非线性特性的准确描述，其效果有待进一步提高。

鉴于此，本文在课题组前期研究的基础上，以Q3黄土为研究对象，基于分数阶导数理论，考虑蠕变特性中等速蠕变及加速蠕变的非线性特征，采用介于理想固体及理想流体之间的Abel黏壶元件代替改进西原模型中的理想固体牛顿黏壶元件，推导建立了分数阶改进西原模型。同时考虑原状及重塑两种类型黄土试样，通过三轴分级循环加-卸载流变试验验证模型的有效性，该研究为实际工程中解决黄土流变问题提供了重要的理论依据。

1 分数阶导数基本原理

1.1 基于Riemann-Liouville分数阶微积分理论

相比于整数阶模型，分数阶模型的发展直至1990年才被广泛重视，其主要包括了Caputo、Grunwald-Letnikov和Riemann-Liouville(R-L)3种基本形式。上述3种基本形式中：一般通过引入积分定义即可以对微积分的计算过程进行简化，因此本文采用了R-L积分定义的形式。Riemann-Liouville分数阶微积分的定义为：设f在(0，+∞)上逐段连续，且在[0，+∞]的任何有限子区间上可积，对t>0，Re(γ)>0，称：

(1)

对上述分数阶积分进行逆运算，可以得到Riemann-Liouville分数阶导数的基本方程为式(2)所示，具体可描述为：设f∈C，ν>0，m是大于γ的最小整数，记ν=m-γ>0，则可得：

(2)

式(2)称为函数f(t)的γ阶Riemann-Liouville分数阶导数(Kilbas et al.，2006)。

1.2 基于分数阶导数的流变元件

传统的Newton元件代表着理想流体的含义，Hooke元件代表理想固体，由分数阶导数建立的流变元件即Abel元件(也被称为Scott-Blair元件)可以理解为是介于理想固体与理想流体之间的一种本构关系。根据模型中黏滞系数是否随时间发生变化，可将Abel元件划分为不随时间变化的常系数Abel黏壶及随时间变化的变系数(主要为考虑损伤特性)Abel黏壶两种形式(周宏伟等，2012)。常系数Abel黏壶的本构关系式如式(3)所示：

(3)

当σ(t)为常数时，对式(3)两侧进行分数阶积分，即可得到常系数Abel黏壶描述的流变关系式如式(4)所示：

(4)

在流变过程中，黄土的黏性系数ηγ不再恒为常数，引入损伤变量D来描述ηγ的劣化，其理论关系式为式(5)：

D=1-e-αt(0≤D<1)

(5)

式中：α为与黄土材料性质相关的系数。

将式(5)代入式(3)可得到考虑损伤变量的变系数Abel黏壶的本构关系为式(6)：

(6)

当σ(t)为常数时，对式(6)两侧进行分数阶积分，即可得到变系数Abel黏壶描述的流变关系如式(7)所示：

(7)

2 流变本构模型的建立

2.1 整数阶改进西原模型

黄土的典型流变过程一般分为3个阶段，包括减速流变阶段、等速流变阶段和加速流变阶段。夏才初等(2008)根据不同应力水平下的加卸载蠕变试验曲线，将弹性、黏性、弹塑性、黏弹性、黏塑性、黏弹塑性力学模型进行不同的串联组合，建立了15个流变力学模型，提出了统一流变力学模型理论。邓亚虹等(2015)基于统一流变力学模型理论，在三轴循环加卸载流变试验的基础上，建立由西原体与村山体串联组合而成的整数阶改进西原模型，如图1所示。

根据上述所建立的整数阶改进西原模型，考虑西原体中黏塑性体与村山体中黏弹塑性体两者之间屈服应力的大小关系，可以建立如图2所示的不同应力水平下的蠕变模型特征曲线。

由图2所示的蠕变模型特征曲线可知：

(1)在加载瞬间，各应力水平作用下均有瞬时弹性变形，反映出该本构模型中应串联有单独的弹簧元件。

(2)在低应力水平作用下，蠕变曲线为减速蠕变类型，卸载后其变形基本能完全回弹，说明具有黏弹性体元件。

(3)在较高应力水平作用下，卸载后蠕变变形有且仅有部分回弹，可以说明此时模型中必然存在黏弹塑性体元件。与此同时，蠕变试验结果表明减速蠕变的变形大于卸载后产生的滞后回弹变形，由此可以说明模型中应同时含有黏弹性体元件和黏弹塑性体元件。

(4)在高应力水平作用下，蠕变试验曲线出现了等速蠕变现象，且最终出现了加速蠕变现象，可见在低应力作用下模型的元件失去了作用，只有当应力达到一定值时才起作用，该元件称为黏塑性体。

2.2 基于Abel黏壶的分数阶改进西原模型

通过对蠕变模型特征曲线分析发现，本课题组已经建立的如图1所示的改进西原模型可以较全面地反映Q3黄土在三轴循环加卸载流变试验条件下的变形特性，描述其蠕变变形规律。但深入分析发现，无论是弹簧原件、黏弹性体元件、黏弹塑性体元件、黏塑性体元件都具有线性元件模型的特征。而黄土是一种典型的非线性土体材料，为了更为有效、真实地模拟黄土的非线性变形特征，在模型中考虑将代表理想流体的牛顿黏壶替换为介于理想固体与理想流体之间的Abel黏壶，建立考虑非线性特性的蠕变本构模型。

进一步分析Q3黄土的蠕变曲线，可以总结出如下特征，在3种应力(低应力、较高应力、高应力)水平作用下呈现出不同的变化特征。具体可描述为低应力水平时的减速蠕变、较高应力水平的减速蠕变、高应力水平的等速和加速蠕变。在第1种情况下，模型中的黏弹性体元件及黏弹塑性体元件的黏滞系数不随时间的变化而变化；第2种情况与第1种情况具有相同的变化特征；第3种情况的等速与加速蠕变特性需要黏塑性体来体现，黏滞系数随时间的变化而产生变化。因此，通过分析可知，在低应力及较高应力水平作用下，因黏滞系数为常数，因此选择常系数的Abel黏壶，而在高应力水平作用下，因黏滞系数不是常数，因此选择变系数的Abel黏壶，由此可构建基于Abel黏壶的分数阶改进西原模型如图3所示。

由图3可知，分数阶改进西原模型由弹性体、黏弹性体、黏塑性体和黏弹塑性体组成。其本构方程按应力大小可描述为不同类型，具体如下：

当σ≤σs1和σs2，即低应力时荷载作用时，首先是模型中弹性体元件的弹簧发生瞬时弹性变形，其次则为黏弹性体元件发生减速蠕变变形，在加载完成进行卸载作用，则加载产生的变形完全回弹。根据式(3)、式(4)关系可得本构方程为：

(8)

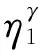
当σs2<σ<σs1，即较高应力时，弹性体、黏弹性体和黏弹塑性体发生变形，卸载后变形部分回弹，其本构方程为：

(9)

当σ≥σs1和σs2，即高应力时，模型整体均发生变形，蠕变曲线出现加速蠕变阶段，根据式(6)、式(7)关系可得其本构方程为：

(10)

综上所述，建立分数阶改进西原模型的本构方程：

(11)

3 流变试验与模型验证

3.1 流变试验

以西安地区Q3原状及重塑黄土为研究对象，采用CSS-2901TS三轴流变试验仪开展三轴循环加卸载流变试验。试验土样类型为原状土样及重塑土样两种，取原状样时应避免土样扰动，取样完成后应立即装入圆柱状铁皮桶内并用胶带密封；制备重塑土样时，将取回的一定质量的土进行风干、碾碎、过筛、配置含水率，含水率配置时需将水均匀喷洒在土料上表面并搅拌，搅拌后装袋密封并放置保湿皿至少20h以上。试验时，控制目标含水率及干密度，采用分层夯实法进行夯实。原状样与重塑样采用同一含水率(20%)，试验控制条件为固结不排水(CU试验)，加载方式为分级循环加、卸载，加载速率为0.001kPa·s-1，卸载速率为0.005kPa·s-1。固结时间为24h，固结后进行加卸载蠕变试验，衡量变形稳定的标准为24h内变形量小于0.05mm。试验完成后将所采集的试验数据按照Boltzmann原理进行处理后，得到了Q3原状与重塑黄土的蠕变试验曲线，如图4所示。

由图4可知，无论是原状黄土亦或重塑黄土，随荷载的作用大小表现出不同的蠕变特性：

(1)在低应力水平阶段，蠕变试验产生的变形较小，如原状黄土荷载为43.33kPa时，其蠕变变形量为1%，随着时间的增加蠕变变形量趋于稳定，该阶段只发生减速蠕变。

(2)在低应力至较高应力水平阶段，蠕变试验产生的变形有所增加，但增幅较小，相比于低应力阶段，其蠕变变形不能完全回弹，说明该阶段没有单独的黏壶存在。

(3)在高应力水平阶段，蠕变试验产生的变形经历了等速蠕变，并最终出现加速蠕变，可见低应力水平减速蠕变阶段的元件模型失去了作用，进而表明模型中存在有黏弹塑性体。

(4)对比原状黄土和重塑黄土的蠕变试验曲线，发现原状黄土的变形量小于重塑黄土的变形量，变形量差别由1%～7%到10%～40%。

3.2 模型参数拟合与验证

为了验证本文所建立的分数阶本构模型的正确性，将其与3.1节的试验数据绘制在一张图中，得到不同固结压力下原状黄土和重塑黄土的拟合曲线(图5、图6)。从图可知，模型拟合曲线与试验数据吻合较好，其相关系数达到了0.99，可见本文所建立的基于Abel黏壶的分数阶改进西原模型本构模型可以完整地描述Q3黄土流变的3个阶段。

为进一步分析本文所建立的分数阶本构模型与邓亚虹等(2015)所建立的改进西原模型之间所存在差异，将两者绘制在同一张图中(图7)进行分析。由图7可知，在加载初期(时间较小)的减速蠕变阶段，分数阶本构模型蠕变应变变化曲线更为圆滑，尤其是重塑黄土体现更为明显；在应力卸载后的蠕变变形阶段，同样呈现出该现象，说明本文所建立的分数阶本构模型可以较好地模拟黄土的流变特性。

在模型验证的基础上，需要对模型中各参数进行求解。最小二乘法作为数据处理中确定模型参数最常用的方法之一，其包含的列文伯格-马夸尔特法(Levenberg-Marquardt，亦称之为LM算法)是最小二乘法算法中的一种，其是利用梯度法求最大(小)值来解决曲线最小二乘拟合问题(Madsen et al.，2004；朱杰兵等，2010；何志磊等，2016)，该方法具有梯度法和牛顿法的优点，收敛速度更快。

表1 Q3原状黄土模型参数拟合结果Table 1 List of Q3 original loess model parameter fitting results

表2 Q3重塑黄土模型参数拟合结果Table 2 List of Q3 remodeling loess model parameter fitting results

4 参数敏感性分析

根据表1拟合结果，将拟合得到第3组参数代入式(11)，仅改变求导阶次γ，可得到不同γ对应的蠕变曲线(图8)。

由图8可知，求导阶次对蠕变特性具有一定的影响，具体可表现为求导阶次为0.1次时，其应变小于2.5%，随着求导阶次的逐渐增加，其应变逐渐增加，当求导阶次为0.9时，其应变近2.9%，表明蠕变变形在逐渐增加，但瞬时弹性变形速率则随着求导阶次的增加逐渐减小。

同时，考虑与黏性系数有关的材料参数α对蠕变特性的影响，绘制不同材料参数α下蠕变应变与时间关系曲线如图9所示。由图可知，材料参数为0.1时，其蠕变应变最小，随着材料参数的增加，其蠕变应变逐渐增加，但增加的幅值较小，其瞬时弹性变形基本一致，区别在于最终蠕变应变的大小具有一定差异，材料参数由0.1变化至0.9时，应变差异近10%。

5 结 论

(1)基于分数阶导数理论，考虑蠕变特性中等速蠕变及加速蠕变的非线性特征，引入一种介于理想固体与理想流体之间的分数阶常系数与变系数Abel黏壶，建立了分数阶改进西原模型并推导出本构方程。

(2)基于Q3原状与重塑黄土的三轴循环加卸载流变试验数据，对模型进行了对比分析。结果表明分数阶改进西原模型既能实现对Q3黄土减速蠕变、等速蠕变和加速蠕变3个流变阶段的模拟，可以弥补整数阶改进西原模型无法描述加速蠕变阶段，所建立的方程能很好地预测其蠕变变形特性及变形规律，所得模型参数可以直接用于Q3原状与重塑黄土的蠕变数值分析。

(3)通过对模型参数进行敏感性分析，发现求导阶次和与黏性系数有关的材料参数增加则蠕变变形均逐渐增加，但求导阶次增加瞬时弹性变形速率逐渐减小，与黏性系数有关的材料参数瞬时弹性变形基本不变。