基于改进NSGA-2-DE算法的综合能源系统运行优化

2022-10-06李贞涛张国军刘守恒

沈阳工业大学学报 2022年5期

李媛，李贞涛，张国军，刘守恒

(1. 沈阳工业大学理学院，沈阳 110870； 2. 华能辽宁清洁能源有限责任公司安全生产部，沈阳 110000； 3. 国家电投东北新能源发展有限公司生产技术部，沈阳 110000)

资源短缺和污染物排放量的不断增加使得环境问题同社会发展的矛盾日益突出，要想实现可持续发展战略，节能减排是必经之路.因此，优化能源结构、提高资源利用率等问题受到了国内外学者的广泛关注[1-2].冷热电联供型综合能源系统，通过多种能源联合供应的方式提高能源利用率[3].因此，深入对冷热电联供型综合能源系统各微源之间协调运行的研究，对于提高系统的经济性与环保性、减少资源的浪费、优化能源结构有着重要的意义.

目前，冷热电联供型综合能源系统运行优化研究主要考虑经济和环保两个方面.胡荣、孙亮等[4-5]建立了基于经济、能源和环境因素的冷热电联供系统模型，采用多目标优化算法得出Pareto最优解[6].但在建立综合能源系统模型时，只考虑了蓄电池一种蓄能装置，当某时段系统产生的冷、热能超出用户需求时，会造成能源的浪费.耿健等[7]基于具有蓄能装置的冷热电联供系统，构建了一种考虑经济和环境的多目标优化模型，分析了引入储能设备以及能源价格对综合能源系统经济性、环保性的影响.蒋润花等[8]为进一步节约运行成本、减少能源浪费，分析了天然气价格和分时电价对综合能源系统各优化策略的影响.上述文献在考虑系统对环境的影响时，只是将CO2、SO2等污染气体的排放量相加，没有考虑到其治理价格之间的差异，因此，不能充分反映其对环境的危害程度.

针对多目标优化问题，常用的算法有SPEA、MOPSO、NAGA-2[9]、MOEA/D[10]等，其中NSGA-2算法是目前能遴选出Pareto最优解的快速、准确的算法[11]，但其在解决复杂问题时存在收敛性与分布性较差的缺点.Li等[12]提出了一种基于DE算法的改进NSGA-2算法(NSGA-2-DE).该算法提高了算法的计算速度和精度，但在染色体修复、放缩因子的选择和非支配排序方式等方面还存在缺陷.

本文建立了含蓄热、蓄冷多蓄能装置的综合能源系统运行优化模型，分析了分时电价与蓄能装置对综合能源系统经济性与环保性的影响.对NSGA-2-DE算法进行改进，提出了一种基于ENS-SS快速非支配排序的改进NSGA-2-DE算法，该算法进行了如下改进：1)采用ENS-SS排序法，以加快非支配排序速度；2)采用随机修复法修复变异过程中违反约束条件的基因，以提高全局搜索能力；3)在变异过程中采用基于正态分布的放缩比例因子，以提高搜索能力和收敛速度.

1 综合能源系统

为提高能源利用率，本文引入蓄冷、蓄热装置，建立了一种含多种蓄能装置的综合能源系统运行优化模型，其结构图如图1所示.

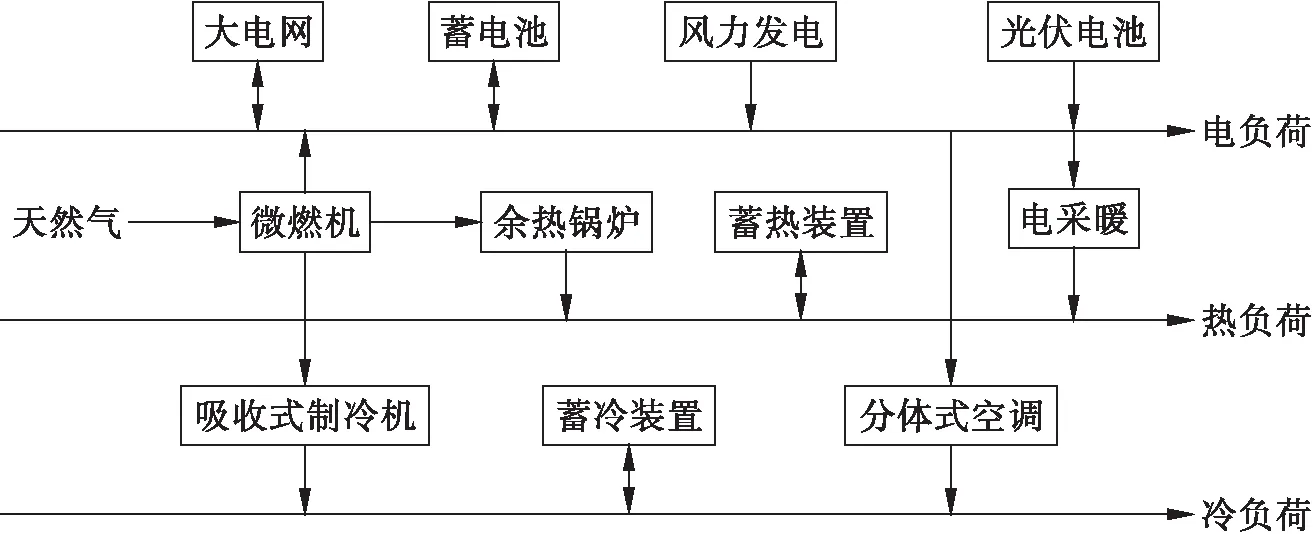
图1 综合能源系统结构Fig.1 Integrated energy system structure

综合能源系统中，电负荷主要由微燃机、风力发电、光伏电池提供，蓄电池存储多余电量，并根据分时电价向大电网购售电能.热负荷由余热锅炉提供，不足部分由电采暖补充.冷负荷由吸收式制冷机提供，分体式空调补充剩余冷负荷.蓄冷装置和蓄热装置用于存储多余能量，避免资源浪费的同时，还能缓冲各微源产生的能量波动.

1.1 微源模型

本文所构建的综合能源系统模型中，微燃机、余热锅炉和吸收式制冷机起到关键作用，其中微燃机燃料费用与发电功率的关系表达式为

(1)

式中：Ca为燃料费用；Qa和ηa为发电功率和效率系数；W为天然气价格；M为天然气低位热值；Δt为调度区间.

余热锅炉和吸收式制冷机利用微燃机产生的高温高压气体进行制热和制冷，计算数学模型为

(2)

式中：Qhw和Qcw为余热锅炉和吸收式制冷机的功率；Bh和Bc为制热、制冷系数；φ(t)为高温高压气体进入余热锅炉的流量比例.

1.2 目标函数

为保证系统的经济效益，本文考虑分时电价，根据电价的峰谷差异向大电网购售电能，以降低运行成本.运行成本包括购电费用、燃气费用以及各微源的维护费用，计算数学模型为

(3)

式中：f1为总运行成本；Qj和Ij为微源j的功率和单位维护成本；Qg(t)和Kt为购售电的功率和分时电价.

为减少污染物的排放量，本文将CO2、SO2、NOx三种污染物的治理费用最小值作为优化目标，通过单位治理价格、污染物排放系数来计算环境成本，计算数学模型为

(4)

式中：f2为环境成本；i=1、2、3时分别为三种污染物；Vi为污染物的单位治理价格；Qa(t)为微燃机功率；χg，i和χa，i分别为大电网和微燃机的排放系数.

1.3 约束条件

首先，为保证用户的冷热电负荷需求，需满足电负荷、热负荷及冷负荷平衡约束，即

(5)

式中：EL(t)、HL(t)和OL(t)分别为电、热、冷负荷；Em(t)、Hm(t)和Om(t)分别为放电、放热、放冷微源；Ee(t)为耗电微源.

其次，应保证各微源的运行功率在其最大功率范围之内，即

Qi，min≤Qi(t)≤Qi，max

(6)

式中，Qi(t)为第i个微源的功率.

最后，由于蓄能装置并不能产生能量，因此在一个调度周期应维持容量不变，同时还要保证剩余能量不低于最大容量的20%.蓄能装置容量约束的数学表达式为

(7)

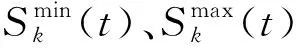
2 改进NSGA-2-DE算法

NSGA-2-DE算法是在传统NSGA-2算法的基础上，引入差分进化算子进行的改进，提高了算法的收敛性和分布性.本文提出了一种基于ENS-SS快速非支配排序的改进NSGA-2-DE算法.该算法主要对NSGA-2-DE算法做了如下改进：

1) 为提高非支配排序速度，采用ENS-SS高效非支配排序法[13]进行非支配排序.对于目标函数最小化问题，首先按照第一个目标函数的适应度对种群P中的N个解进行升序排列，若两个解的第一个目标函数适应度相同则按照第二个目标函数的适应度排序.将排序后的种群记为P′={p1，p2，…，pN}.

在完成排序后，开始将P′中的个体分配到不同的前沿中.由于一个解不可能被排序靠后的解支配，因此只需要和已经被分配到前沿的解进行比较，就足以确定该解所在的前沿[13].从第一个解p1到最后一个解pN，依次与已分配的解进行比较，确定其所在前沿，直到所有的解都被分配.

2) 在采用差分变异算子进行变异的过程中，某些变异后个体染色体上的基因会超过约束条件的范围，对于这部分染色体一般采用舍弃或者修复的方法.对在变异过程中违反约束条件的染色体，采取随机修复策略，修复表达式为

(8)

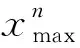
3) 在变异过程中采用基于正态分布的放缩比例因子.差分进化算子的变异过程表达式为

Ui=X1+ψ(X2+X3)

(9)

式中：Ui为Xi交叉时的目标基因；X1、X2、X3为Xi变异时随机选取的三个个体；ψ为放缩比例因子.ψ越大则算法的全局搜索能力越强，但收敛速度会变慢.为提高算法的搜索能力和收敛速度，本文采用基于正态分布的放缩比例因子，当个体Xi发生变异时，变异表达式为

(10)

式中：α为随机变量，取值范围为(-∞，+∞)；μ和σ为可变参数，需根据实际工程问题进行调整.根据正态分布密度函数的性质可知，μ和σ分别决定了放缩比例因子所在位置和离散程度，σ越大，算法的全局搜索能力越强，但结果的稳定性越差.

改进NSGA-2-DE算法的流程如图2所示，虚线处为主要改进部分.算法的具体流程如下：

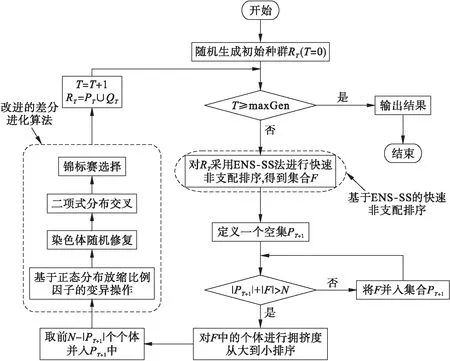
图2 改进NSGA-2-DE算法流程Fig.2 Flovo chart of improved NSGA-2-DE algorithm

1) 初始化.设进化代数T=0，种群规模为N，随机生成初始种群RT(规模为2N).

2) 若T≥maxGen(最大迭代次数)则返回Pareto最优解集，否则继续步骤3.

3) 快速非支配排序.将种群RT中个体采用ENS-SS法进行快速非支配排序，将排序后的个体按照其层级分配到不同的非支配面集合F中.

4) 定义一个空集合PT+1，将F依次并入集合PT+1中，直至|PT+1|+|F|>N(|P|表示集合P中的元素个数).

5) 拥挤距离计算.计算F内个体的拥挤距离，并按照拥挤距离从大到小对其进行排序，最后取前N-|PT+1|个个体，并入集合PT+1中.

6) 首先对PT+1中的个体按照式(10)进行变异操作、按照式(8)进行染色体随机修复，其次对变异后的个体进行二项式分布交叉，最后对交叉后的个体进行锦标赛选择，得到新的数量为N的种群QT.

7) 令T=T+1，RT=PT∪QT，并转到步骤2.

3 算例分析

3.1 基础数据

为验证本文所提模型及改进NSGA-2-DE算法的有效性，以某综合能源系统数据为例进行仿真[14-15].该系统利用某典型的冷、热、电负荷如图3所示、风力发电机和光伏电池出力测试数据如图4所示.

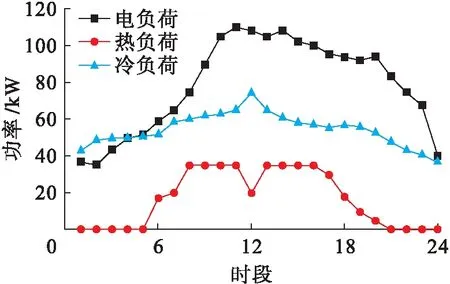
图3 冷、热、电负荷Fig.3 Cooling，heating and power loads

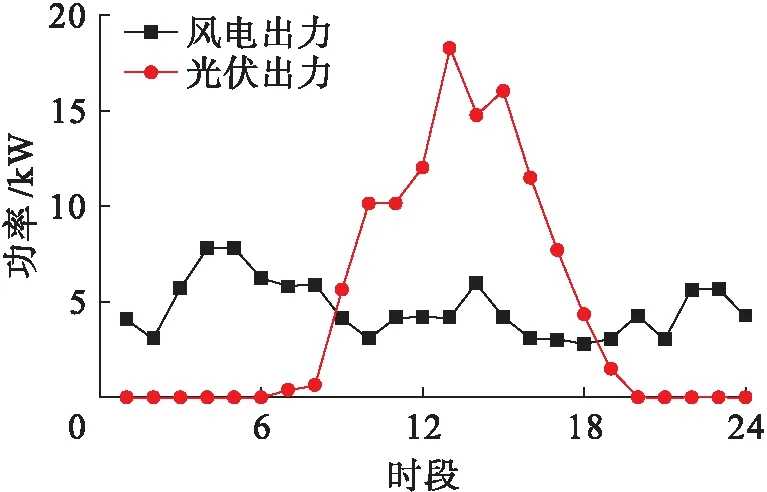
图4 风力发电机和光伏电池的出力Fig.4 Power of wind turbines and photovoltaic cells

分时电价如表1所示、污染物单位治理价格如表2所示、模型所包含的11个微源的功率上下限和维护价格如表3所示.微燃机的燃料为天然气，价格为3.25元/m3，低位热值为9.7 kWh/m3，余热锅炉和吸收式制冷机的制热、制冷系数分别取0.95和1.2，蓄电池和蓄热、蓄冷装置的容量分别为500、150和150 kWh.

表1 分时电价Tab.1 Time-of-use electricity prices

表2 污染物治理价格Tab.2 Pollutant treatment cost 元/kg

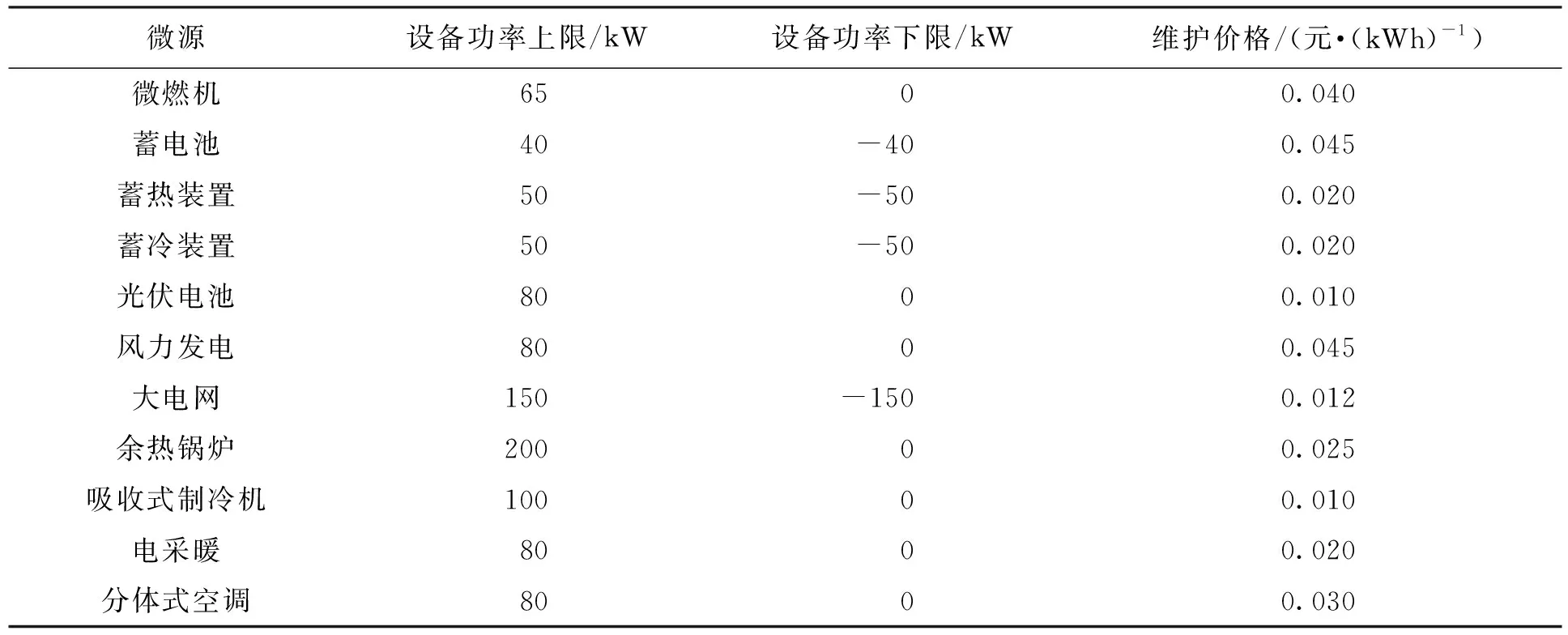
表3 微源相关数据Tab.3 Relevant data of micro-sources

3.2 模型仿真及算法分析

3.2.1 模型仿真

本文采用改进NSGA-2-DE算法对模型进行优化调度.以一天24 h为调度周期，1 h为调度时段，每个时间段内有8个优化变量，分别为：电网、微燃机、蓄电池、蓄冷装置、蓄热装置、电采暖、分体式空调的运行功率以及高温高压气体进入余热锅炉的比例.

种群数量取100，种群中个体的每一维坐标代表着某微源一个时间段内的出力情况，维度为192.最大迭代次数设为50 000次，采用可行性法则处理约束条件，仿真结果保留100个Pareto最优解，即用户可选择的方案.放缩比例因子ψ通常选取0.5，根据计算结果中环境成本和运行成本的大小及Pareto最优解的离散程度，对参数μ和σ进行调整，本文μ和σ分别取0.5和0.01.

为证明最优方案的优越性，对其进行分析，该方案中各微源的出力如图5所示，蓄电池功率及容量如图6所示.结合图5～6可以看出：1)1∶00～8∶00电负荷相对较低，且电价处于谷值，因此系统向大电网购电，蓄电池不断储存电能.8∶00时电价回归峰值，蓄电池向大电网出售电能.2)11∶00～16∶00电负荷需求大，电价处于平时，微燃机大功率输出，蓄电池放电保证用户的电能需求.3)18∶00～22∶00电价回归峰值，系统减少向大电网购电，蓄电池放电保证用户用电需求.4)23∶00～24∶00电负荷降低，且电价为谷值，系统从大电网购电储存到蓄电池中，保持蓄电池容量的稳定.

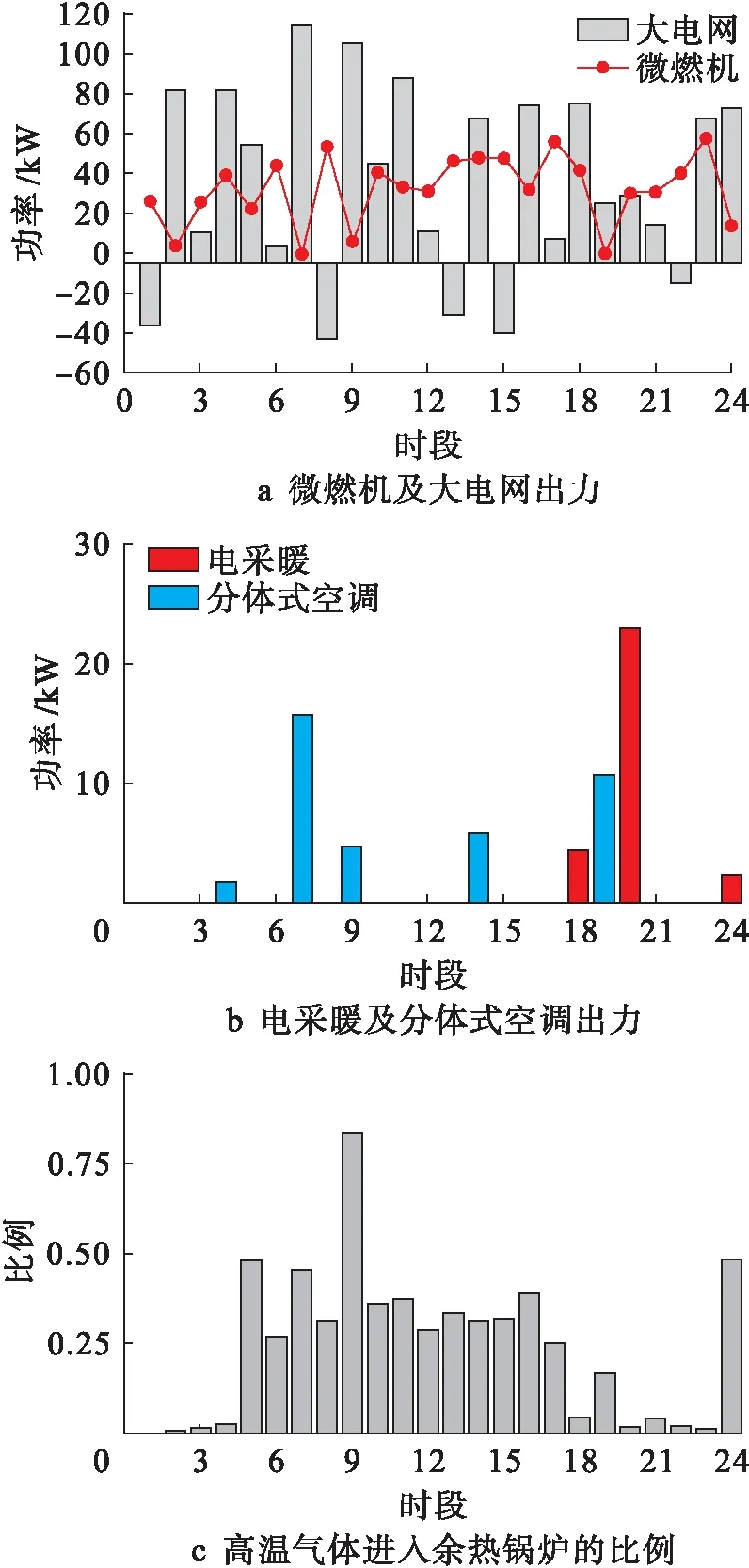
图5 各微源的出力情况Fig.5 Power of each micro-source

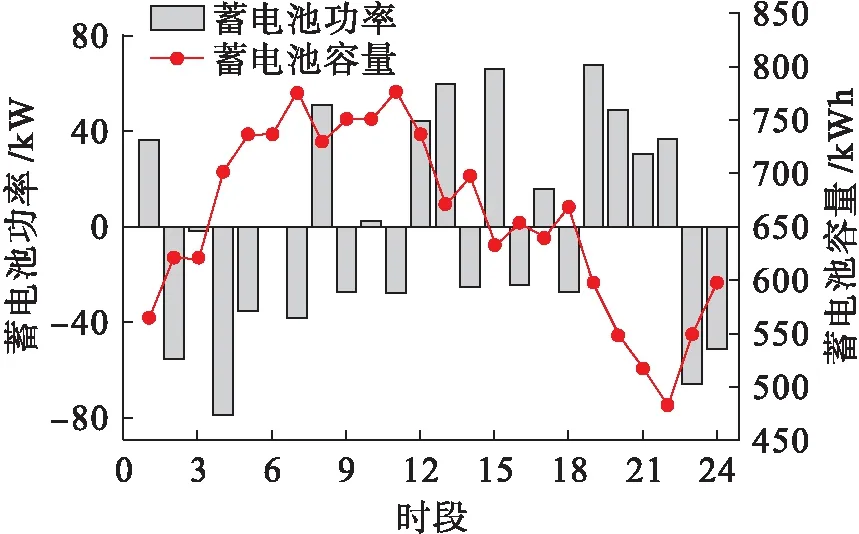
图6 蓄电池功率及容量Fig.6 Power and capacity of battery

图7是蓄热装置的出力及容量情况，结合图5可以看出：1)1∶00～6∶00热负荷低，余热锅炉功率较低.6∶00～9∶00热负荷增大，蓄热装置放热，高温高压气体进入余热锅炉的比例增大.2)10∶00～18∶00微燃机功率较大，热负荷主要由余热锅炉提供，不足部分由电采暖补充.3)19∶00～23∶00热负荷减小，高温高压气体大量进入吸收式制冷机，热负荷主要由蓄热装置和电采暖提供.4)24∶00时为保证蓄热装置容量平衡，余热锅炉功率加大，同时电采暖也开始工作，产生的热能储存在蓄热装置中.

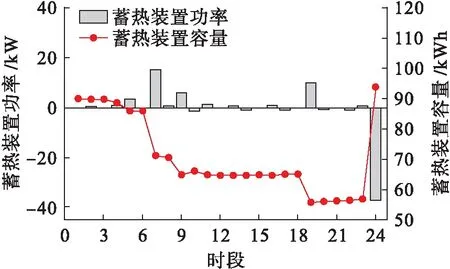
图7 蓄热装置功率及容量Fig.7 Power and capacity of heat storage device

图8是蓄冷装置的出力及容量情况，结合图5可以看出：1)5∶00～9∶00由于冷负荷增加，且吸收式制冷机的功率降低，蓄冷装置释放冷能，不足的部分由分体式空调补充.2)10∶00～18∶00由于微燃机的功率较大，冷负荷大多由吸收式制冷机提供，不足的部分由分体式空调补充，蓄冷装置不断储存冷能.3)19∶00时由于微燃机功率的减小，蓄冷装置和分体式空调同时工作保证用户的用冷需求.4)20∶00～次日4∶00冷负荷主要由吸收式制冷机提供，蓄冷装置储存冷能以保证容量平衡.

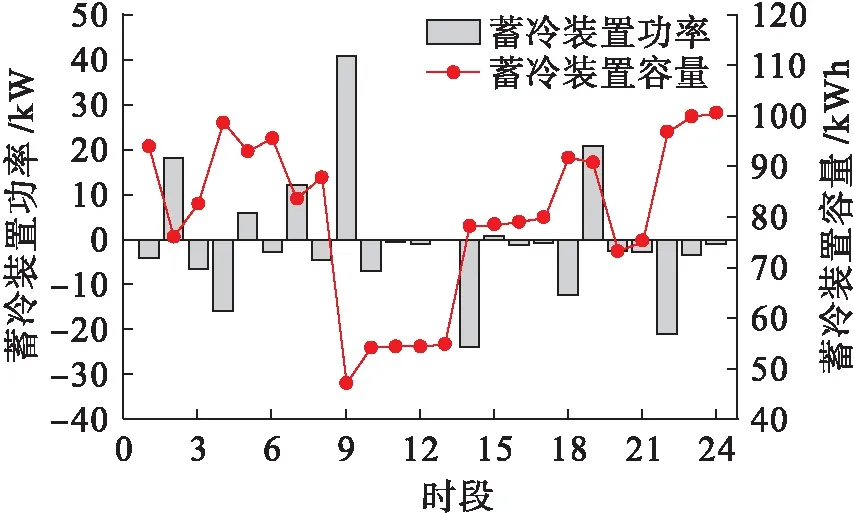
图8 蓄冷装置功率及容量Fig.8 Power and capacity of cool storage device

3.2.2 算法比较

为证明改进NSGA-2-DE算法的优越性，针对本文所提的综合能源系统模型及数据，采用NSGA-2算法、NSGA-2-DE算法同改进NSGA-2-DE算法进行对比.设置三种算法的种群数量均为100、迭代次数均为50 000次，最终结果都保留100个Pareto最优解，并采用TOPSIS法选取最优方案.NSGA-2、NSGA-2-DE算法所得Pareto最优解集如图9所示.由图9对比可以看出：NSGA-2算法求得的Pareto最优解有明显的间断；而NSGA-2-DE所得结果无明显间断点，且NSGA-2-DE算法所得最优点更靠近中间位置.

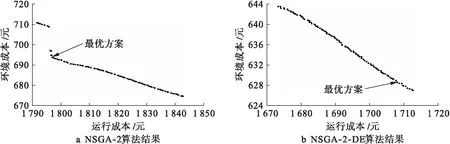
图9 传统算法得到的Pareto最优解集Fig.9 Pareto optimal solution set obtained by conventional algorithms

为了更好地说明改进NSGA-2-DE算法的优越性，将三种算法所得最优方案进行对比，对比结果如表4所示.由表4中数据可以看出：1)改进NSGA-2-DE算法的计算时间比NSGA-2算法慢了7.56 s，但其运行成本和环境成本分别减少了93.94元和128.77元.2)改进NSGA-2-DE算法的计算时间比NSGA-2-DE算法快了45.56 s，虽然其优化结果的运行成本提高了0.62%，但其环境成本降低了11.02%.3)改进NSGA-2-DE算法和NSGA-2-DE算法所得结果中系统消耗的总电能大致相等，但前者电采暖和分体式空调的总功率都在30～40 kW之间，而后者具有明显的差异，说明陷入了局部最优.因此，改进NSGA-2-DE算法在计算速度和优化结果上都要优于NSGA-2-DE算法；与NSGA-2算法相比计算速度相差不大，但优化结果明显更好.