仿生缓冲器的等效刚度与抗冲击性能分析

孙自强， 刘 川， 金映丽， 闫 明

(沈阳工业大学 机械工程学院， 沈阳 110870)

海军舰船受到水下非接触爆炸产生的冲击波、气泡脉动和滞后流的冲击作用，船体结构可能依然保持完整，但其内部设备却遭到破坏.为了保障舰船设备在冲击作用下正常工作，往往为舰船设备安装缓冲器[1-5].

近年来，关于仿生隔振系统的研究越来越多，Wu等[6]受动物肢体结构的启发，研究了肢体结构在被动隔振中的非线性特性；Dai等[7]提出了一种用于捕捉太空垃圾的新型仿生抗冲击机械手，从理论和实验两个方面研究了该系统的动力学响应和缓冲性能；Hu等[8]基于仿生X形结构和六自由度Stewart平台的非线性刚度和非线性阻尼特性，设计了一种被动六自由度隔振平台，并对其隔振性能进行了实验研究；Wang等[9]研究了一种新型n层垂直非对称X形结构模型，分析了其非线性刚度及非线性阻尼特性和隔振动态响应.Sun等[10]以n层剪式桁架结构隔振平台为研究对象，研究被动、半主动、主动隔振系统的设计以及非线性隔振的优势.

为满足舰船稳定性要求，舰船的重心不能过高，所以要尽量降低设备的高度，如此也能降低设备受冲击时的倾覆力矩.因此，本文提出一种与经典缓冲器相比，能降低设备高度的仿生缓冲器，用Lagrange法建立仿生缓冲器的动力学模型，对系统动力学方程和等效刚度进行分析，用龙格库塔法计算仿生缓冲器的抗冲击性能.

1 仿生缓冲器原理

1.1 原理模型

该仿生结构模仿动物弯曲肢体，在膝盖处加上弹簧阻尼系统，并与另一端相连，如图1所示.仿生缓冲器由连杆、弹簧阻尼系统和相应的旋转接头组成，缓冲器上端与设备连接，下端与基础或甲板连接，其原理模型如图2所示，k和c分别代表缓冲器中弹簧阻尼系统的刚度和阻尼.

图1 仿生结构Fig.1 Bionic structure

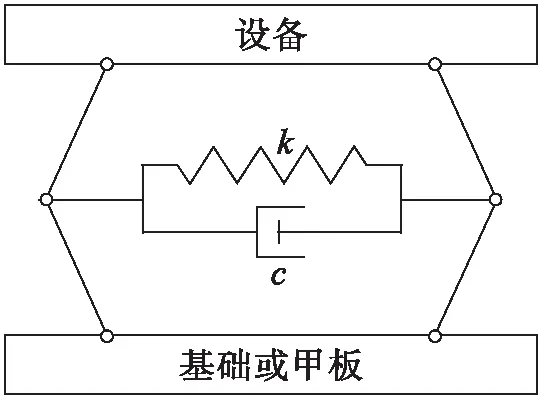
图2 原理模型Fig.2 Principle model

1.2 仿生缓冲器的运动方程

仿生缓冲器的几何关系如图3所示，m为设备质量，y1和y2分别为设备和基础的位移，l为四根连杆的长度，θ为四根连杆的安装角度，h为弹簧阻尼系统的位移，x为弹簧阻尼系统的长度变化量，φ为连杆的旋转角度.不考虑连杆和旋转接头的质量及其之间的摩擦力，求解仿生缓冲器在垂向的动力学方程.

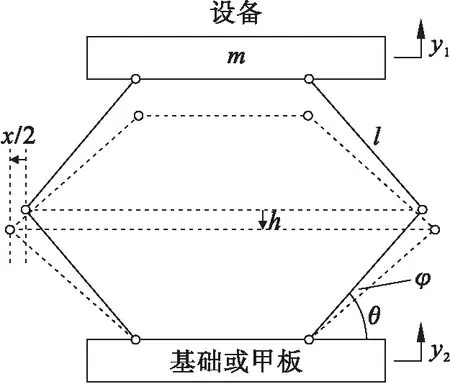
图3 几何关系Fig.3 Geometric relationship

由图3可知，x和φ可以根据y1、y2坐标确定.根据系统水平和垂直方向的运动可得

(1)

lsinθ-h=lsin(θ-φ)

(2)

设备与基础之间的相对位移为

(3)

弹簧阻尼系统的位移为

h=(y2-y1)/2

(4)

x和φ可以表示为

(5)

(6)

式中，φ的取值范围为-θ<φ<90°-θ.

系统总动能为

(7)

系统势能为

(8)

式中：k为弹簧阻尼系统的刚度；x0为弹簧阻尼系统的初始变形量.

拉格朗日函数[11]为

L=T-V

(9)

拉格朗日方程[12]为

(10)

式中，D为能量耗散函数，其表达式为

(11)

整理可得系统动力学方程为

(12)

系统垂向刚度力为

(13)

系统垂向阻尼力为

(14)

由式(13)和(14)可以看出，仿生缓冲器的垂向刚度力和垂向阻尼力是非线性函数，其数值由杆长、连杆安装角度和弹簧阻尼系统的长度变化量所确定.

(15)

(16)

将式(15)和(16)代入系统动力学方程得

(17)

式中：β0=0；β1=tan2θk；

式(17)即是经过二阶泰勒展开后简化的系统动力学方程.

1.3 仿生缓冲器的等效刚度

为了探究连杆长度和连杆安装角度对仿生缓冲器等效刚度的影响，计算得到相对位移与垂向刚度力之间的运动规律.仿生缓冲器的初始结构参数如表1所示.

表1 初始结构参数Tab.1 Initial structure parameters

在仿生缓冲器其它初始结构参数不变的条件下，系统不同连杆长度下的等效刚度曲线如图4所示，系统不同连杆安装角度下的等效刚度曲线如图5所示.

图4 杆长对等效刚度的影响Fig.4 Influence of rod length on equivalent stiffness

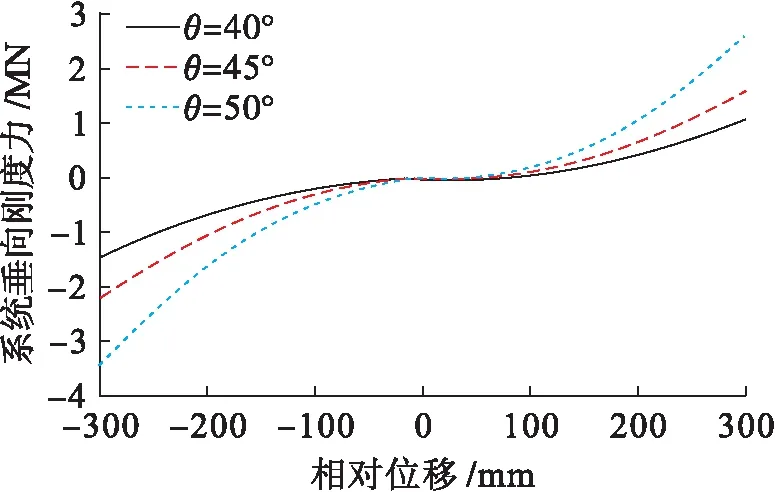
图5 安装角度对等效刚度的影响Fig.5 Influence of installation angle on equivalent stiffness

由图4、5可以看出，随着相对位移的增大，垂向刚度力的增大速度越来越快，仿生缓冲器的等效刚度越来越大，即呈现刚度硬化的特性.随着连杆长度的减小和连杆安装角度的增大，等效刚度的非线性越明显.因此，仿生缓冲器的非线性刚度受系统结构参数的影响.

2 与经典缓冲器结构的对比

该仿生缓冲器通过调整弹簧阻尼系统的安装位置来降低缓冲系统中设备的高度.选取两个长度相等的弹簧阻尼系统，将其分别放在经典缓冲器和仿生缓冲器中，通过调整连杆的长度以及连杆安装角度可以使设备的高度降低，仿生缓冲器与经典缓冲器结构的对比如图6所示，图中H1=H2.

图6 结构对比Fig.6 Comparison of structures

由图3、6可以看出，仿生缓冲器中设备的高度d与连杆长度l、连杆安装角度θ之间的关系表达式为

d=2lsinθ

(18)

由式(18)可知，仿生缓冲器中设备的高度随连杆长度、连杆安装角度的减小而减小.在仿生缓冲器初始结构参数条件下，与经典缓冲器相比，仿生缓冲器使系统中设备的高度降低了64.65%.

3 冲击响应计算及分析

通过Lagrange法和泰勒公式得到式(17)简化的系统动力学方程，再利用四阶龙格库塔法计算其冲击响应.对于冲击激励，根据德国军标BV043-85定义的正负双半正弦波信号对缓冲器基础施加冲击输入.将仿生缓冲器与经典缓冲器的抗冲击性能进行对比.设两个系统的基础遭受正波峰值125.6g，负波峰值31.4g，正波脉宽为5 ms，负波脉宽为20 ms的正负双半正弦波加速度冲击，加载的冲击载荷波形如图7所示.

图7 冲击载荷Fig.7 Impact load

将仿生缓冲器与经典缓冲器的刚度系数和阻尼系数分别设置为1×106N/m、6 700 N·s/m.经过仿真计算可知，仿生缓器的连杆安装角度越大，系统的相对位移幅值越小，但是考虑到安装角度越大，设备的高度会增大，综合考虑将连杆安装角度θ设置为60°，得到仿生缓冲器与经典缓冲器的相对位移响应对比曲线和加速度响应对比曲线，如图8、9所示.

图8 相对位移响应曲线Fig.8 Relative displacement response curves

图9 加速度响应曲线Fig.9 Acceleration response curves

为评价仿生缓冲器的抗冲击性能，需要计算其相对于经典缓冲器的峰值降低率.系统的相对位移峰值降低率为

(19)

式中：u1为经典缓冲器的相对位移峰值；u2为仿生缓冲器相对位移峰值.

系统的加速度峰值降低率为

(20)

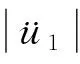
由图8、9可以看出，两种缓冲器的相对位移峰值和加速度峰值都呈现衰减趋势，所以仅考虑最大峰值的变化量.经典缓冲器的最大峰值为21.245 mm，出现在0.012 3 s；仿生缓冲器的相对位移最大峰值为16.243 mm，出现在0.011 2 s.由式(19)计算得：系统的相对位移最大峰值降低了23.54%.

经典缓冲器的加速度最大峰值为112.26g，出现在0.002 3 s；仿生缓冲器的加速度最大峰值为103.41g，出现在0.002 1 s.由式(20)计算得：系统的加速度最大峰值降低了7.88%.与经典缓冲器相比，在仿生缓冲器连杆安装角度为60°时，系统的相对位移峰值和加速度峰值都有所降低，所以仿生缓冲器具有更好的抗冲击性能.

4 结 论

通过上述分析可以得到如下结论：

1) 仿生缓冲器的等效刚度呈非线性特性.随着相对位移的增大，垂向刚度力的增大速度越来越快，仿生缓冲器的等效刚度越来越大，呈现出刚度硬化特性.在其它参数一定的情况下，随着连杆长度的降低和连杆安装角度的增大，仿生缓冲器等效刚度的非线性越明显.

2) 与经典缓冲器相比，仿生缓冲器能有效降低设备的高度.当仿生缓冲器的连杆安装角度为60°时，仿生缓冲器具有更好的抗冲击性能.