高超声速圆柱绕流中驻点热流的稀薄效应*

李宪开，张志雨，何淼生，朱斌镔，柳 军

(1. 国防科技大学 空天科学学院， 湖南 长沙 410073; 2. 沈阳飞机设计研究所扬州协同创新研究院有限公司， 江苏 扬州 225000; 3. 上海交通大学 航空航天学院, 上海 200240)

临近空间高超声速飞行器气动设计需要准确预测壁面热流，工程经验及理论公式在近连续流区内逐渐失效[1-3]，数值模拟方法仍然是壁面热流预测的主要工具。然而，当来流克努森数(Kn)大于0.01时，即便是简单的高超声速平板绕流问题仍然因方法的不同而存在较大差异[3-4]。

对于稀薄高超声速流场，直接模拟Monte Carlo(direct simulation Monte Carlo, DSMC)方法被认为是最可能准确预测壁面热流的方法[5]。该方法虽物理上满足Boltzmann方程并对其进行直接模拟[6]，但并不能直接给出稀薄流场热流输运的数学方程。目前，基于宏观方程的数值方法还无法在全流域范围内获得与DSMC结果一致的热流结果，这说明高超声速流动驻点热流输运中稀薄效应的作用机制还不够清楚。

从工程应用的角度来看，纳维-斯托克斯(Navier-Stokes，N-S)方程的应用是最广泛的，其对热流模拟的基础是Fourier热传导定律。但是，将其直接应用于稀薄高超声速流场会获得偏高的热流结果[2-3]，最直观的原因是壁面速度滑移或温度跳跃现象的出现，故而从20世纪80年代至今发展了诸多滑移或跳跃边界条件来拓展N-S方程在稀薄流域的应用[7-9]。Maccormack[7,9]等提出的通用型滑移或跳跃边条可使N-S方程在Kn=0.25的高超声速圆柱绕流计算中获得与DSMC误差不大于10%的驻点热流结果，但二者的流场结果具有极大的差异[10-11]。近期研究表明[12-14]，对于简单的高超声速圆柱绕流和平板绕流问题，即使采用更趋近于真实物理的高阶滑移或跳跃边界条件、非平衡边界条件也无法获得与DSMC一致的壁面附近流场信息。

从气体物理的角度来看，随着Kn的增大，局部流场的分子速度分布不再满足平衡态Maxwell分布，也不再满足线性本构关系和Fourier热传导关系。近年来，不少学者在拓展流体动力学方程上做了大量的研究，以其准确模拟稀薄流域流动问题，包括Eu-type方程[15-16]、Burnett-type方程[17]等。例如，Eu-type方程可以在Kn=0.25、Ma=10的圆柱绕流中获得与DSMC误差不大于10%的驻点热流结果[15]。有趣的是，非线性驻点热流输运的相关研究[1-2]表明：基于Burnett方程的二阶热流展开项对非线性热流的贡献为正，即稀薄效应下的高阶热流表达应为Fourier热流加上二阶热流项，然而却发现DSMC结果低于N-S方程Fourier热流，这一矛盾被归因于展开项系数的不确定性。

此外，对于稀薄高超声速流场的解析还可以采用基于速度分布函数计算的气体动理学方法，包括气体动理论统一算法[18]、统一气体动理学格式[19]和多尺度粒子方法[20]等，这一类多尺度方法的研究也是近十几年来稀薄计算的热点。值得一提的是，这一类方法的发展通常采用DSMC方法结果作为验证的标准[5]，本文内容属机理讨论，因此采用最可能准确的DSMC方法开展研究。

总结上述两个角度的调研，我们不难发现热流输运中的稀薄效应表现在两个方面：一是壁面速度滑移和温度跳跃现象，使得真实热流低于Fourier热流[3,7-8]；二是非线性本构关系和非线性热传导，虽基于Burnett方程展开项分析获得较Fourier热流偏高的结果[2-3]，但诸多计算数据却获得非线性热流低于Fourier热流的观点[2-3,10]。前述两点稀薄效应的描述均基于宏观上的理解和认识，在微观层面上的理解较少，然而深入的理解对进一步发展准确的驻点热流预测方法是至关重要的。因此，本文从Fourier热传导定律失效的观点出发，基于DSMC方法对Kn为0.01～0.1、Ma为5～10的高超声速圆柱绕流驻点热流中的稀薄效应进行研究，旨在从微观视角上给出连续方法高估驻点热流的新理解。

1 问题描述

研究对象为半径R=0.152 4 m的二维高超声速圆柱绕流，以文献[3]中Kn=0.05的算例为参照，通过改变来流压力实现Kn为0.01～0.1的变化范围。研究的物理问题如图1所示，为规避热力学非平衡带来的影响，来流气体选为氩气(Ar)，相关的气体参数如表1所示。

图1 物理问题示意Fig.1 Schematic diagram of physical problem

表1 氩气相关气体参数

本文计算的算例分为两组，第一组为不同来流Kn的算例，该组中Case-1至Case-10的来流Kn从0.01等差增长至0.1，公差为0.01；第二组为不同来流Ma的算例，该组中Case-1至Case-11的来流Ma从5等差增长至10，公差为0.5。第一组算例中来流Ma固定为10，第二组算例中来流Kn固定为0.05。

2 方法介绍

采用DSMC方法开展微观视角下的数值研究工作，该方法是以唯象论为物理基础，并借助以往稀薄气体流动的模拟经验和数理统计知识而发展起来的一种计算算法，由Bird教授于20世纪70年代提出[6]。DSMC方法并不是直接对Boltzmann方程进行求解，而是从物理上模拟了一个与Boltzmann方程描述一致的气体流动过程。20世纪90年代，Wagner[21]证明了DSMC方法的控制方程实为Boltzmann方程，自此之后DSMC方法才在高超声速领域发挥重要作用。

DSMC方法的具体介绍本文不再赘述，详细内容可参考Bird的专业书籍[6]。本文中采用的分子模型为可变径硬球(variable hard sphere, VHS)模型，气-壁相互作用过程通过Maxwell模型实现完全漫反射的固定壁温边界条件。对于VHS模型，可根据Chapman-Enskog理论和分子动力学理论获得以下几个平衡态参数的定义：

1)平衡态分子平均自由程为：

(1)

2)参考温度下黏性系数可表述为：

(2)

3)黏性系数幂次关系式为：

(3)

4)热传导系数定义为：

(4)

式(1)～(4)中各参数的含义可参考Bird专业书籍[6]，这里不再赘述。

针对驻点热流展开讨论，采用三种不同的热流计算方式。第一种是DSMC壁面热流微观统计结果，下文中采用“DSMC_data”来表示。DSMC的壁面热流需要统计所有撞击壁面的模拟分子的能量，如式(5)所示。

(5)

式中：qDSMC_data为壁面热流密度；treal为真实物理时间；A为单位面积；e是单子气体分子能量，包括平动能、转动能和振动能，上标in和re分别代表了入射壁面和从壁面反射离开的模拟分子。

此外，为对比连续方法和微观粒子算法在热流结果上的差异，还采用了Fay-Riddell关系式作为第二种热流表达方式，下文用“F-R correlation”表示，该关系式可写成：

(6)

式中，各参数含义可参考文献[22]，本节不再赘述。

第三种热流表达方式耦合了DSMC流场计算结果和Fourier热传导定律，即基于DSMC流场温度的Fourier热流，下文用“DSMC_Fourier”来表示，具体表达式为：

(7)

式中：κ为热传导系数，可由式(4)求得；η为壁面法向方向。

最后，为使不同来流条件下的热流具有可比性，采用来流参数对其进行无量纲化：

(8)

3 结果与讨论

3.1 不同稀薄效应下驻点热流规律

图2所示为不同来流Kn下驻点热流变化规律，横坐标为来流Kn的1/2次方，纵坐标为热流系数cq。其中：“F-R correlation”通过式(6)求得；“DSMC_data”为DSMC壁面热流结果，由式(5)确定；“DSMC_Fourier”为基于DSMC流场温度的Fourier热流结果，由式(7)求得。此外，图2中采用蓝色十字图标标出了文献[3]中的无滑移N-S方程的结果，与红色实线的匹配结果可验证本文F-R关系式的正确性。

图2 不同表达方式驻点热流随来流Kn的变化规律Fig.2 Trend of stagnation point heat fluxes with different Kn

根据式(6)的推导，容易得到F-R关系式热流结果与Kn1/2成正比，图中“F-R correlation”曲线所示亦如此。黑色虚线所示的DSMC壁面热流结果从Kn1/2>0.1(Kn>0.01)开始逐渐偏离F-R关系式预测结果，偏离程度随Kn增大而增大，并且不再保持与Kn1/2的线性关系。前述观察到的现象具有共识性，基于对稀薄效应的宏观认识(壁面滑移或跳跃现象)可以较好地理解。

有趣的是，黑色实线所描述的基于DSMC流场温度的Fourier热流结果“DSMC_Fourier”与DSMC壁面热流结果存在差异。这意味着即便N-S方程等连续方法能够借助于壁面滑移或跳跃边界条件获得与DSMC结果一致的宏观流场，也不能得到准确的壁面热流结果。更详细地，不同Kn下“DSMC_Fourier”驻点热流较DSMC微观统计结果高，且相对误差随着Kn的增加逐渐从20%减小至10%左右，这隐喻着Fourier热传导定律的失效。

通常，稀薄效应由来流密度变小或研究对象变小所引起，可以理解为流场状态的稀薄程度，如图2所示的Kn变化。来流Ma增大，会使激波及壁面附近的梯度增大，进而局部Kn随之增大，可以理解为流动的稀薄程度。图3给出了不同来流Ma时，三种不同热流表达方式下的驻点热流变化规律。可以看到，由来流Ma引起的稀薄效应增强同样使得驻点热流结果增大，但三种不同表达方式下的热流增长具有差异性。黑色虚线所示的DSMC壁面热流结果均小于F-R关系式预测结果，且二者的差异随来流Ma的增加而增大。此外，“DSMC_Fourier”所示的Fourier结果在当前Ma范围内仍然高估驻点热流，且相对误差随着Ma的增加逐渐从24%减小至12%左右。

图3 不同表达方式驻点热流随来流Ma的变化规律Fig.3 Trend of stagnation point heat fluxes with different Ma

总结图2与图3所示的热流差异规律，可以做如下理解：

1) F-R关系式等连续方法与DSMC微观统计的驻点热流之间的差异主要由温度跳跃现象引起，这是稀薄效应的第一种体现；

2) 基于DSMC宏观温度的Fourier热流和DSMC微观统计的驻点热流之间的差异表明，Fourier热传导定律不再适用于稀薄高超声速驻点热流的预测，这是稀薄效应的第二种体现。

上述两点理解通过两种宏观现象阐述，还需要基于微观视角进行进一步的解释，主要回答两个基础问题：一是温度跳跃现象的微观理解是什么？二是稀薄效应下Fourier热传导定律的失效机制是什么？后续两个小节将分别针对前述两个基础问题展开。

3.2 驻点温度跳跃现象的微观理解

通常认为，F-R关系式及N-S方程等连续方法在稀薄条件下高估热流的主要原因是未考虑壁面滑移或跳跃现象。如同设计温度跳跃边界条件一样，这是基于宏观的一种认识，通常借助局部克努森数来设计。局部克努森数可定义[8]为：

(9)

式中，Q是温度、速度和压强等流场宏观参数，η为壁面法向方向。

此外，一种简单且常用的温度跳跃边界条件可以是Smoluchowski跳跃边界条件[7,9]：

(10)

若采用温度计算KnGLL并代入跳跃边界条件，可以得到：

(11)

由于壁面附近温度变化不算太大，式(11)中γ和Pr可作常数处理。因此可认为在当前计算范围内，式(11)所示的比值基本保持不变。

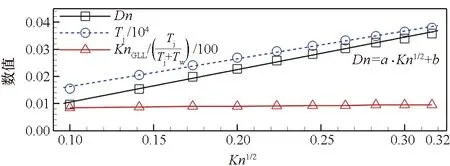
式(10)或式(11)为温度跳跃的数学或宏观表达式，为印证其合理性，统计了不同来流Kn和来流Ma下式(11)左侧所示的比值变化规律，如图4中带三角符号的红色直线所示。可以看到，该比值同Kn和Ma基本保持无关性，这表明在当前考虑的稀薄效应程度下，采用KnGLL衡量连续介质假设失效下的温度跳跃现象是合适的，文献[10]也表明采用式(10)所示的温度跳跃边界条件可以在Ma=10、Kn=0.05条件下获得与DSMC误差不超过10%的驻点热流结果。

(a) 来流Kn变化(a) Freestream Kn changes

在微观层面，当边界层内、外存在足够大的温差时可以认为温度跳跃现象必然存在。无论第一层网格多小，其内所含模拟分子不可能全部由壁面反射分子组成，第一层网格的物理量变化更多地取决于其他网格和该网格之间的流通量。故而，第一层网格宏观温度必然大于壁面温度，而这种跳跃温差取决于分子间碰撞频率的大小。当流动逐渐偏离平衡态时，分子间碰撞频率会减小，可能入射的模拟分子群和壁面反射分子群之间的碰撞减少，导致壁面附近流体温度越发高于壁面温度，温度跳跃现象增强。基于上述理解，定义一个微观统计量非平衡度Dn来表征当地流场的非平衡度：

(12)

式中，νsimu为DSMC碰撞过程中实际的碰撞频率，νtheo为VHS模型对应的理论平衡态碰撞频率。那么，Dn=0为平衡态，Dn>0或Dn<0为非平衡态。值得注意的是，采用的氩气为单原子分子，因此这里的非平衡指的是分子速度分布偏离Maxwell平衡态分布，也可称为平动非平衡。

为验证前述所提出的偏离非平衡态和温度跳跃之间的关系，图4中列出了不确定度Dn、温度跳跃Tj和来流Kn、来流Ma之间的关系。为保证Dn和Tj在同一坐标中具有可比性，图中蓝色虚线所示为温度跳跃的万分之一倍(Tj/104)。从图4中不难发现，Dn和Tj均与Kn和Ma呈一次线性正相关关系。此外，图中Dn与Tj曲线的斜率是十分接近的，可认为非平衡度在一定程度上可以用于描述温度跳跃的大小，这也表明了温度跳跃现象在微观层面上是由流动偏离平衡态所引起。

3.3 Fourier热传导定律的失效机制

回顾图2和图3中所示的热流规律可知，基于DSMC流场温度的Fourier热流结果与DSMC壁面热流仍然存在差异，这表明稀薄效应增强时，采用Fourier定律描述沿驻点线的热流输运是不合适的。通常认为该问题由线性本构关系失效导致，进而发展了诸多高阶热流关系式来解决该问题。然而，类如Wang、Singh等的研究工作表明二阶热流项的贡献为正[1-2]，体现在壁面热流上应该获得较Fourier热流更大的结果，但数值结果获得相反的结论。

本节通过对比DSMC和基于DSMC流场温度的Fourier表达沿驻点线的热流结果，尝试给出线性Fourier热传导定律的微观失效机制。图5所示为Kn=0.01、Ma=10的高超声速圆柱绕流驻点线热流输运结果，其中“DSMC_Fourier”为基于DSMC流场温度的Fourier热流，由式(7)计算求得；“DSMC_data”为DSMC微观统计结果，通过对网格内模拟分子的能量进行统计而写成热流通量的形式[23]。

(13)

式中：c为矢量热运动速度；int为单个气体分子的内能，包括转动能及振动能。当气体为单原子时，略去式(13)第二项。

图5 驻点线热流输运及非平衡度变化趋势Fig.5 Variation of the heat transfer and non-equilibrium degree along the stagnation streamline

根据热运动速度分解，可写出x方向上的热流通量表达式[23]：

(14)

此外，由于速度分布偏离平衡态分布是线性本构关系不再成立的内在原因，因此图5中还给出了沿驻点线的非平衡度Dn的变化趋势，如图中蓝色曲线所示。

图5中，绿色实线所示的“DSMC_Fourier”线性热流输运在激波内和壁面附近与DSMC微观统计结果存在明显差异。另外，蓝色曲线所示的非平衡度在激波和壁面附近均大于零(分子速度分布偏离平衡态)，可认为局部稀薄诱导的非平衡效应是Fourier热传导定律不再适用的本质原因。更详细地，线性Fourier表达在激波内低估传热，在壁面附近高估传热。激波内大梯度引起的偏离平衡态分布和壁面附近大梯度引起的偏离平衡态分布在分布形式上是不同的，尽管两种偏离均引起碰撞频率的减小，但最终引起的线性热传导失效是不同的。另外，还可以观察到一个有趣的现象：非平衡度的峰值并没有对应着热流最大的位置，而是比较靠近激波的前边界，也许这也是诸多可计算气体动理学方法在激波前缘位置与DSMC结果吻合不太好的缘故。

图5右上角的红色实心圆点为DSMC驻点热流结果，该结果高于壁面第一层网格内的DSMC微观统计热流。对比了所有算例的第一层网格热流和驻点热流，结果表明：驻点处第一层网格热流均小于驻点热流。并且，该差异随Kn和Ma的增大而增大，在本文计算的最小Kn和最小Ma条件下，二者是十分接近的。第一层网格热流和壁面热流之间的差异正是温度跳跃存在的一种证明。

此外，绿色曲线所示的“DSMC_Fourier”热流输运在靠近壁面几层网格内出现了突增的现象，本文所计算的算例均出现了不同程度的Fourier热流突增现象，并且这种突增现象均发生在距离壁面约3倍当地分子平均自由程的空间内。正好，根据Maxwell速度分布可知，在一个平均碰撞时间内95%以上的分子可自由移动的距离均在3倍分子平均自由程内。同理，从壁面反射的分子在无分子间碰撞的条件下可自由移动的距离基本上均小于3倍分子平均自由程，即壁面反射分子直接影响流场的作用范围约为3倍分子平均自由程。因此，将观察到的Fourier热流突增现象解释为壁面约束效应，这和文献[24]中观察到的近壁面分子平均自由程变化规律在物理上是相通的。

为量化前述壁面约束效应，表2列出了各算例条件下的Fourier热流突增的强度，表中的数值为近壁面3倍分子平均自由程范围内的Fourier热流最大值和最小值之比。从表2中可看到，量化Fourier热流壁面约束效应的比值随Kn的增大而减小，也随Ma的增大而减小。因此，来流Kn和Ma的增大均使得Fourier热流突增减弱。回顾图5中“DSMC_Fourier”曲线，壁面附近平动非平衡效应使Fourier表达高估热流，壁面约束效应同样使Fourier表达高估热流。图4和表2表明，壁面附近平动非平衡度随Kn、Ma增加而增加，壁面约束效应随Kn、Ma增加而减弱。二者共同作用下，Fourier表达下的驻点热流高于DSMC结果，且相对偏差随Kn、Ma增加而减小，从而可认为壁面约束效应对Fourier热传导失效的贡献更大。

表2 壁面约束效应下Fourier热流突增强度规律

由于DSMC方法的特点是随机，虽获得了流场的非平衡度描述，但无法确定哪些模拟分子代表非平衡态，哪些模拟分子代表平衡态。也正由于模拟分子的随机碰撞和自由移动，可在统计壁面热流时以非平衡度的大小按概率统计平衡态热流和非平衡态热流。若非平衡度为0.1，那么与壁面发生碰撞的模拟分子有10%的能量交换统计为非平衡态热流，剩余90%的能量交换统计为平衡态热流。

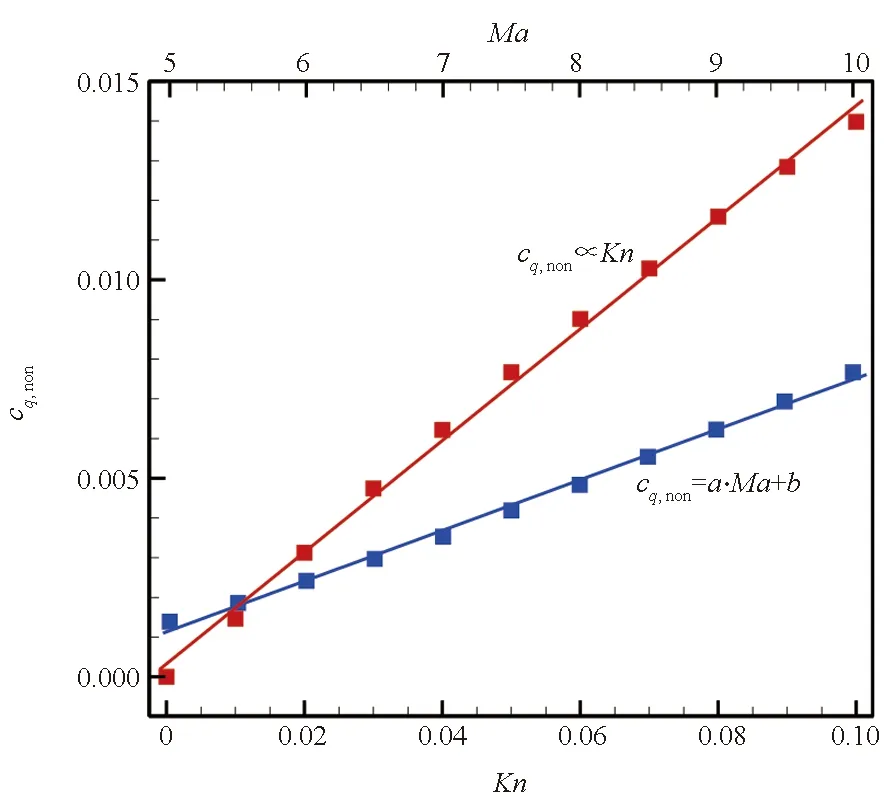
图6 非平衡态热流随来流Kn、Ma的变化规律Fig.6 Variation of the nonequilibrium heat flux with respect to the freestream Kn and Ma

基于上述观点，可获得如图6所示的非平衡态热流随Kn和Ma的变化规律，且容易看到：非平衡态热流与Kn和Ma均呈现出线性正相关关系。同时，由于Kn为零时，流动处于平衡态，此时非平衡态热流也应为零，因此可以认为非平衡态热流与Kn成正比。

4 结论

针对工程上关心的稀薄高超声速驻点热流预测中存在的方法适用性问题，采用Fay-Riddell关系式、DSMC方法和基于DSMC流场温度的Fourier传热三种热流表达方式，对不同来流Kn和Ma的高超声速圆柱绕流驻点热流规律及差异开展了研究，针对经典连续方法在稀薄流区高估驻点热流的现象给出了如下几点理解：

1) 基于微观统计的非平衡度参数Dn和壁面温度跳跃Tj均与Kn、Ma呈线性正相关关系且斜率接近，Dn所描述的平动非平衡正是温度跳跃现象在微观层面上的诱因。温度跳跃会削弱温度梯度导致热流降低，从而无滑移连续方法会高估驻点热流。

2) 流场局部稀薄效应使得壁面附近分子速度分布偏离平衡态，线性本构关系不再保持，Fourier热传导定律失效且高估热流，从而基于DSMC流场温度的Fourier热流高估驻点热流。

3) 受到壁面反射分子的影响，基于DSMC流场温度的Fourier热流在壁面附近约3倍分子平均自由程内高估热流，称之为壁面约束效应，这也是Fourier热传导定律失效且高估驻点热流的第二种体现。