Meixner扭曲函数及其在期权定价中的应用研究*

姚落根， 翁嘉雪， 刘 欢，王敬童

(湖南工商大学 理学院,湖南 长沙,410205)

0 引言

期权定价和保险定价是金融数学研究的重要内容, 本质上都是对未定权益的权利价 值进行定价. 已有研究成果(如Mildenhal[1]等)指出期权定价和保险定价之间只有细微的差别, 这就为这两种定价方法的交叉融合提供了可能. 目前, 期权定价对保险定价 产生了深远的影响, 它强调了保险产品与期权之间的相似性, 因而保险定价可以借助期 权定价的思想与方法. 这方面的研究已取得很多成果, 见文献[2-5]等. 然而, 利用保险 定价方法解决期权定价问题的研究成果很少, 仅见到文献Gerber等人[6-7]和Bladt等[8].值得注意的是, Schmitz[9]用反例证明了Bladt等[8]的结论是错误的. 随着保险证券化的急剧发展, 特别是保险期权的面市, 更是对这种融合提出了现实需要. 因此, 将保险定价方法运用于期权定价具有重要的理论意义和现实意义.

在保险定价理论中, 概率变换是一种常用的风险定价方法. 设随机变量X代表风险, 王树勋[10]利用Choquet积分定义其价格H[X;γ]如下

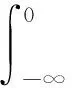
其中SX(x)是X的生存函数,gγ是某个概率扭曲函数. 如果X非负,则H[X;γ]简化为

基于标准正态分布, 王树勋[10]提出了著名的王氏变换

gγ(u)=Φ(Φ-1(u)+γ)，

(1)

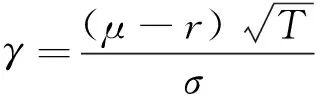
Hamada[14]的结果表明, 在正态收益率时, 利用王氏变换计算期权价格非常有效, 但在非正态收益率时却不尽人意. 金融资产的收益率呈非正态分布特征早已成为人们的共识. 为了适应收益率的非正态特征, 王氏变换有必要进行改进.目前国内外这方面的研究已有一些结果, 王树勋[15]提出了如下的双参数变换替代王氏变换

gν,γ(u)=Tν(Φ-1(u)+γ)，

其中Tv为自由度为v的t分布的分布函数. Kijima & Muromachi[16]考虑了如下变换

gγ(u)=E[Φ(G-1(u))Y+γ]，

其中Y是非负随机变量,G(x)是随机变量U/Y的分布函数,U是与Y独立的标准正态随机变量. Godin等[17]引入了NIG变换

gα,β,δ,γ(u)=ΦNIG(ΦNIG-1(u)+γ)，

其中ΦNIG为NIG分布的分布函数.

为了刻画收益率的非正态性质, 国内外学者提出了很多模型模拟收益率. Meixner过程就是其中之一.Meixner过程的增量分布具有尖峰厚尾性质, 这些性质非常适合刻画资产价格的收益率. 本文利用概率变换思想, 基于Meixner分布定义了一类新的概率扭曲函数——Meixner扭曲函数, 证明了在Meixner模型中, 按Meixner扭曲函数得到的期权价格和在均值修正鞅测度(mean correcting martingale measure)下得到的期权价格一致, 从而说明了按Meixner扭曲函数得到的期权价格无套利. 数值计算结果表明, 按Meixner扭曲函数得到的期权价格非常准确.

1 Meixner分布和Meixner过程

Meixner过程源于正交多项式理论的研究, 首先由Schoutens等[18]引入.后来, Grigelionis[19]将其应用于金融数据的建模. 目前,Meixner过程是金融数学中常见的数学模型.本节将介绍Meixner分布和Meixner过程.

定义1如果随机变量X的特征函数为

(2)

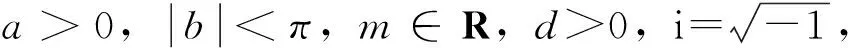
Grigelionis[19]给出了Meixner分布的密度函数

(3)

Meixner分布的各阶矩都存在. 这里仅列出后面参数估计中需要用到的期望(E(X)), 方 差(D(X)), 偏度(Skewness(X))和峰度(Kurtosis(X)),

由于正态分布的峰度为3, 容易看到Meixner分布的峰度总是大于正态分布的峰度.

由(2)式，对任意正整数n有

故Meixner分布无穷可分, 从而可以按如下方式定义Meixner过程.

定义2概率空间(Ω,F,(Ft)t≥0,P) 上的右连左极过程X={Xt,t≥0}称为具有参数(a,b,m,d)的Meixner过程, 如果Xt满足

1.X0=0 a.s.;

2.Xt具有独立增量和平稳增量 ;

3.Xt～M(a,b,mt,dt) .

下面的结论在本文后面定理4的证明和数值实验中需要用到.

定理1设X～M(a,b,m,d),α∈R,β∈R,α≠0, 记Y=αX+β.则

Y～M(a|α|,sgn(α)b,αm+β,d),

(4)

其中sgn是符号函数.特别地, 若Y=-X, 则Y～M(a,-b,-m,d).

证明只需证明Y的特征函数具有(2)形式.

E[exp(iuY)]=E[exp(iu(αX+β))]

由于cosx,coshx都是偶函数, 故

最后等式表明Y～M(a|α|,sgn(α)b,αm+β,d).

2 Meixner扭曲函数

本节基于Meixner分布, 提出Meixner扭曲函数, 并研究Meixner扭曲函数对Meixner分布的影响.

定义3设X～M(a,b,m,d), 称概率扭曲函数

(5)

为Meixner扭曲函数.

与王氏变换只有一个参数不一样,Meixner扭曲函数有5个参数. 本质上,Meixner扭曲函数就是把-X的x分位数向左或向右平移|γ|个单位, 然后重新用-X的分布函数作用. 我们接下来讨论Meixner扭曲函数对Meixner分布的影响.

定理2设X～M(a,b,m,d),h(X)是连续递增的非负函数,Z=h(X).则

(6)

证明因X是连续型随机变量, 故

SZ(x)=P(Z>x)=P(h(X)>x)=P(X>h-1(x))=F-X(-h-1(x)).

将Meixner扭曲函数gγ;a,b,m,d(x)作用于SZ(x)可得

因此, (6)成立.

3 期权定价

本节研究Meixner扭曲函数在期权定价中的应用.

考虑如下几何Lévy市场模型: 市场中有两种资产, 一种为无风险资产, 其价格过程为

Bt=exp(rt).

另一种资产称为股票, 其价格过程为

St=S0eXt,0≤t≤T,

(7)

其中, 无风险利率r和股票初值S0都是正常数,X={Xt,t∈[0,T]}是定义在概率空间(Ω,F,F=(Ft)t∈[0,T],P)上的的Lévy过程. 如果Xt不是布朗运动和泊松过程, 则上述市场模型不完备, 因而存在无穷多个等价鞅测度. 在几何Lévy模型中, 通常选取均值修正鞅测度作为定价测度(参见Schoutens[20]). 均值修正鞅测度的核心思想是通过修正Lévy过程的均值, 使得股票价格过程的折现过程为鞅, 从而得到定价测度. 在Xt为Meixner过程时, 我们把Schoutens[20]的结果总结为如下的引理.

引理1在模型(7)中, 设Xt在市场概率P下是参数为(a,b,m,d) 的Meixner过程, 则执行价格为K、到期日为T的欧式看涨期权(ST-K)+在均值修正鞅测度Q下的价格为

EQ[e-rT(ST-K)+],

(8)

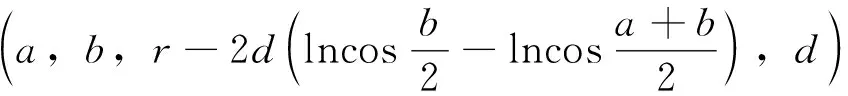
在模型(7)中, 设Xt是参数为(a,b,m,d)的Meixner过程,则XT～M(a,b,mT,dT). 令h(x)=S0ex, 则ST=h(XT). 利用定理2, 我们有

H[ST;-γ]=E[h(XT-γ)]

=S0e-γE[eXT]

=S0e-γeφ(-i)T.

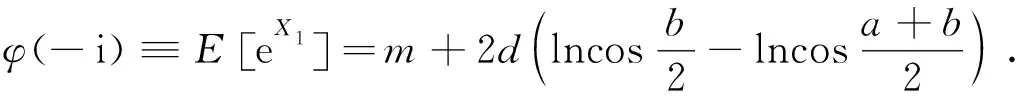
γ*=(φ(-i)-r)T,

(9)

则显然有

H[ST;-γ*]=S0erT.

换言之, 在Meixner扭曲函数g-γ*;a,b,mT,dT作用下, 资产的收益率等于无风险利率.

下面的定理说明在指数Meixner模型中, 由Meixner扭曲函数得到的期权价格等于均值修正鞅测度下的价格.

定理3在模型(7)中, 如果Xt是参数为(a,b,m,d)的Meixner过程, 则

H[e-rT(ST-K)+;-γ*]=EQ{e-rT(ST-K)+},

(10)

其中Q是均值修正鞅测度,γ*由(9)式定义.

证明令h(x)=e-rT(S0ex-K)+, 则h(XT)=e-rT(S0eXT-K)+. 由定理2,

记YT=XT-γ*. 由于在实际概率P下,XT～(a,b,mT,dT), 由定理1可知, 在实际概率P下,YT～M(a,b,mT-γ*,dT). 另一方面,

EQ{e-rT(ST-K)+}=e-rTEQ{(S0eXT-K)+}.

因此, 定理的结论成立.

4 数值实验

本节将对来自五个常用的期权定价模型(B-S模型、Merton跳扩散模型、NIG模型、Meixner模型和VG模型)的模拟数据, 讨论三种扭曲函数(分别基于正态分布、NIG分布和Meixner分布)定价的准确性.

理论上, 在将要讨论的5个模型中, 股票价格的下确界为0, 上确界为+∞. 但在计算机模拟过程中, 必有min{ST}>0,max{ST}<+∞. 同时, 在数值计算中, 需要用经验 分布代函数代替真实分布函数. 这些都会对相对误差产生无法避免的影响. 另外，容易得到当执行价格K大于或等于模拟价格的最大值时, 任何模型下, 三种扭曲算子的相对误差都等于1; 而当执行价格K小于或等于模拟价格的最小值时, 任何模型下, 三种扭曲算子的相对误差都等于exp(-rT)min{ST}/S0. 因此, 对于深度虚值期权和深度实值期权而言, 比较三种扭曲算子的准确性就没有意义. 基于这个原因, 本文主要讨论当执行价格在股票初始价格S0附近时的相对误差.

4.1 B-S模型

在模型(7)中, 令Xt=(μ-0.5σ2)t+σWt, 其中Wt是标准布朗运动. 首先利用参数S0=50,r=0.05,T=0.5,σ=0.15,μ=0.1, 模拟出5 000个股票价格ST. 其次, 利用极大似然估计方法求得NIG分布的参数估计

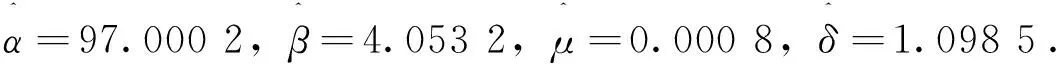
和Meixner分布的参数估计

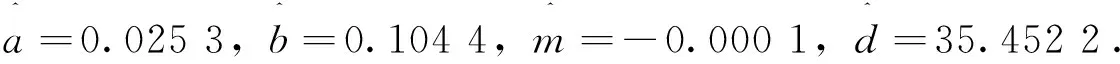
最后利用三种扭曲函数(分别基于正态分布、NIG分布和Meixner分布)计算欧式看涨期权的价格及其相对误差. 由于此次模拟max{ST}=76.254 1, min{ST}=34.803 7, 从图1左图可以看到, 当执行价格不小于76.254 1时, 三种扭曲函数得到的相对误差都为1; 当执行价格K→0+时, 三种扭曲函数得到的相对误差都收敛于

exp(-rT)min{ST}/S0=0.678 9.

从图1右图可以看到, 当执行价格在S0=50附近时, 王氏变换的相对误差最小, Meixner和NIG变换的相对误差几乎没差异, 最大的相对误差不超过6.5%. 因此, 在BM模型中, 由这三种扭曲函数得到的期权价格都非常准确.

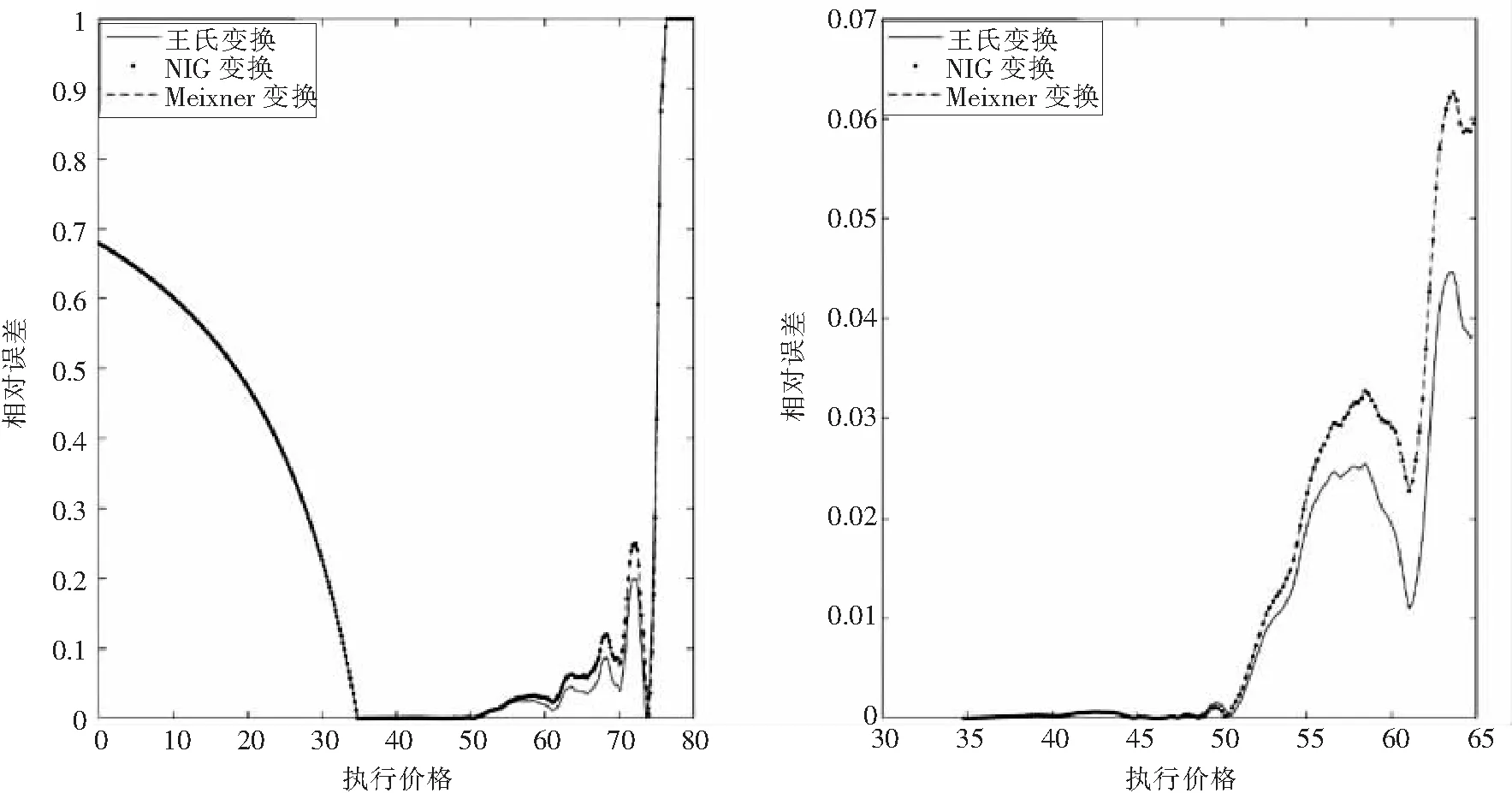
图1 B-S模型中三种扭曲算子价格的相对误差Fig.1 The relative errors of prices of three distortion operators in B-S model

4.2 Merton跳扩散模型

Merton[21]考虑了如下跳扩散模型

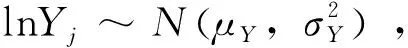
与B-S模型的做法类似, 给定S0=30,r=0.05,T=0.5,μ=-0.1,σ=0.2,λ=1.5,

μY=0.2,σY=0.3. 先模拟出5 000个股票价格ST.利用极大似然估计方法求得NIG分布和Meixner分布的参数分别为

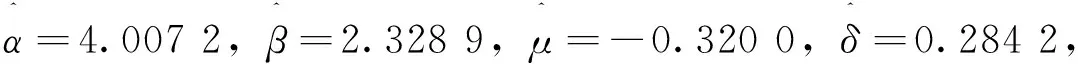
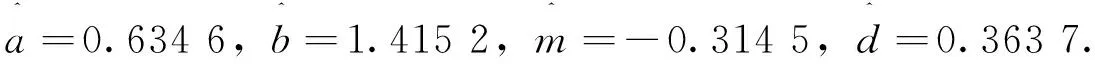
此次模拟max{ST}=173.801 5,min{ST}=6.702 3, 从图2左图可以看到, 当执行价格不小于173.801 5时,3种扭曲函数得到的相对误差都为1; 当执行价格K→0+时,3种扭曲函数得到的相对误差都收敛于exp(-rT)min{ST}/S0=0.217 9. 从图2右图可以看到, 当执行价格在30附近时, Meixner价格和NIG价格比较准确, 相对而言, Meixner价格稍优于NIG价格, 但王氏变换价格比较差.

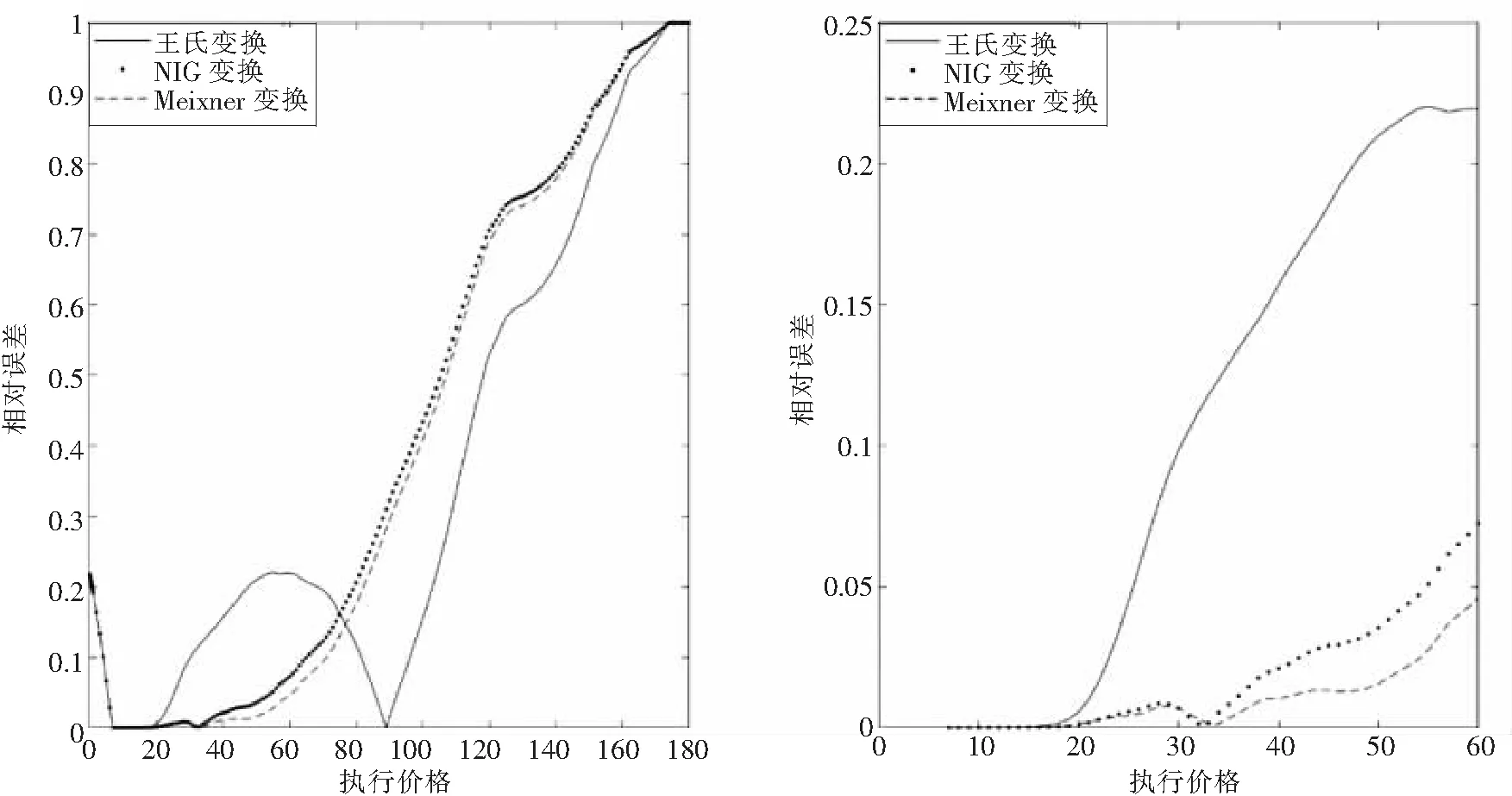
图2 Merton跳扩散模型中三种扭曲算子价格的相对误差Fig.2 The relative errors of prices of three distortion operators in merton jump diffusion model

4.3 NIG模型

在模型(7)中, 设Xt是参数为(α,β,μ,δ)的NIG过程. Godin[17]给出了均值修正鞅测度下, 欧式看涨期权CT=max{ST-K,0}∣的价格为

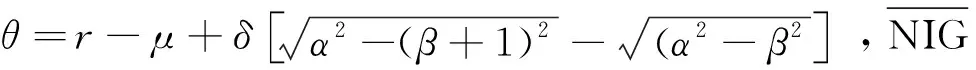
给定S0=30,r=0.08,T=0.5,α=10,β=-0.2,μ=0.1,δ=0.3后, 模拟出5 000个股票价格ST. 利用极大似然估计方法求得Meixner分布的参数为

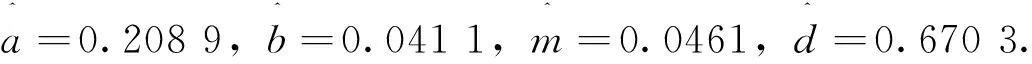
本次模拟max{ST}=59.561 3,min{ST}=16.949 3, 从图3左图可以看到, 当执行价格不小于59.561 3时, 三种扭曲函数得到的相对误差都为1; 当执行价格K→0+时, 三种扭曲函数得到的相对误差都收敛于exp(-rT)min{ST}/S0=0.542 8. 从图3右图可以看到, NIG价格和Meixner价格比较准确, 王氏变换价格比较差.

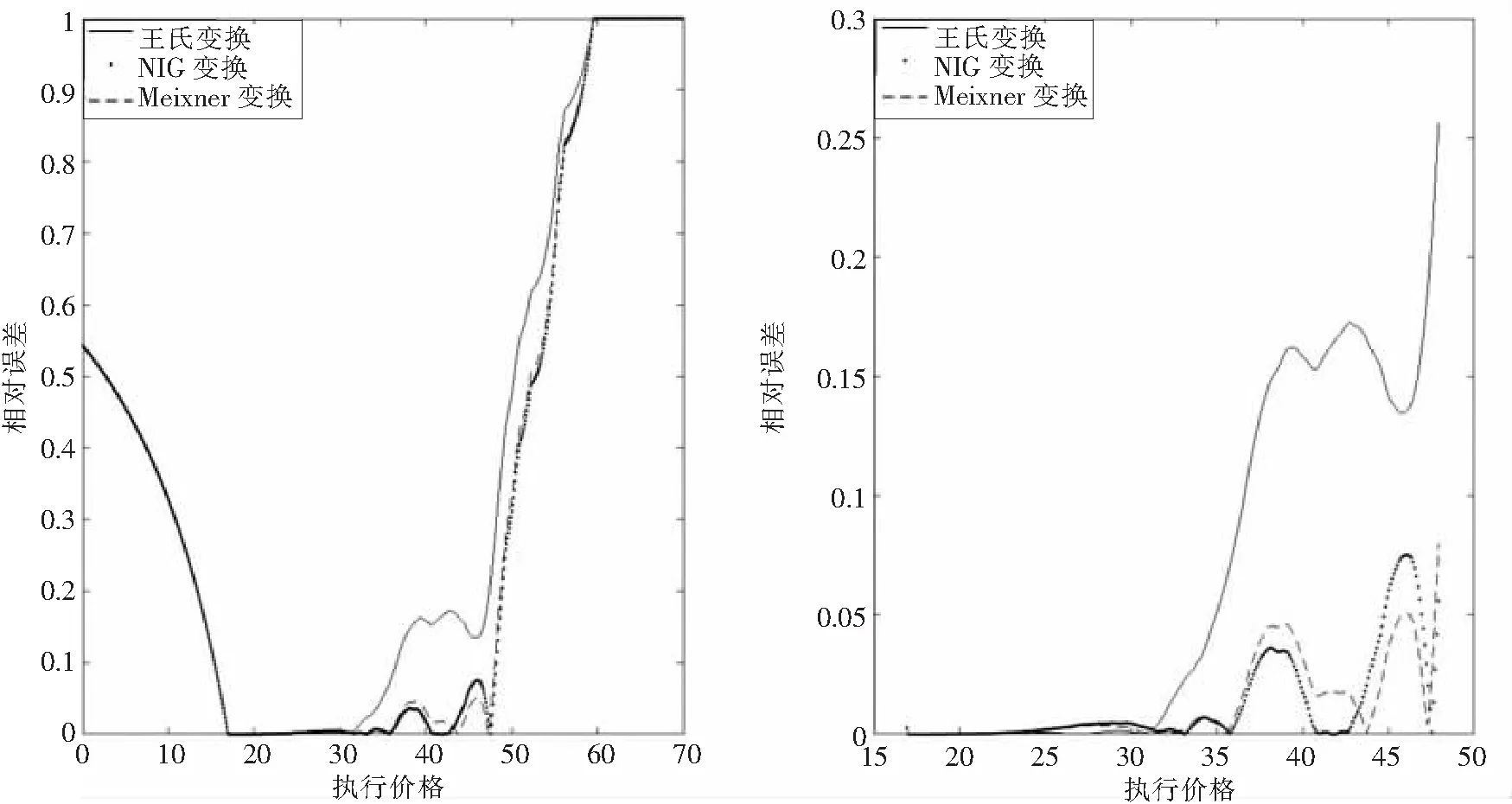
图3 NIG模型中三种扭曲算子价格的相对误差Fig.3 The relative errors of prices of three distortion operators in NIG model

4.4 Meixner模型

设模型(7)中的Xt是参数为(a,b,m,d)的Meixner过程.给定S0=50,r=0.08,

T=0.5,a=0.3,b=-0.1,m=0.15,d=0.2后, 模拟出5 000个股票价格ST.NIG分布参数的极大似然估计值为

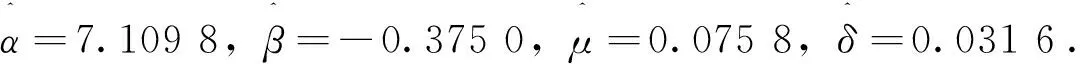
本次模拟max{ST}=142.816 8,min{ST}=15.522 9, 从图4左图可以看到, 当执行价格不小于142.816 8时, 三种扭曲函数得到的相对误差都为1; 当执行价格K→0+时, 三种扭曲函数得到的相对误差都收敛于exp(-rT)min{ST}/S0=0.298 3. 从图4右图仍然可以看到,NIG价格和Meixner价格比较准确, 王氏变换价格比较差.

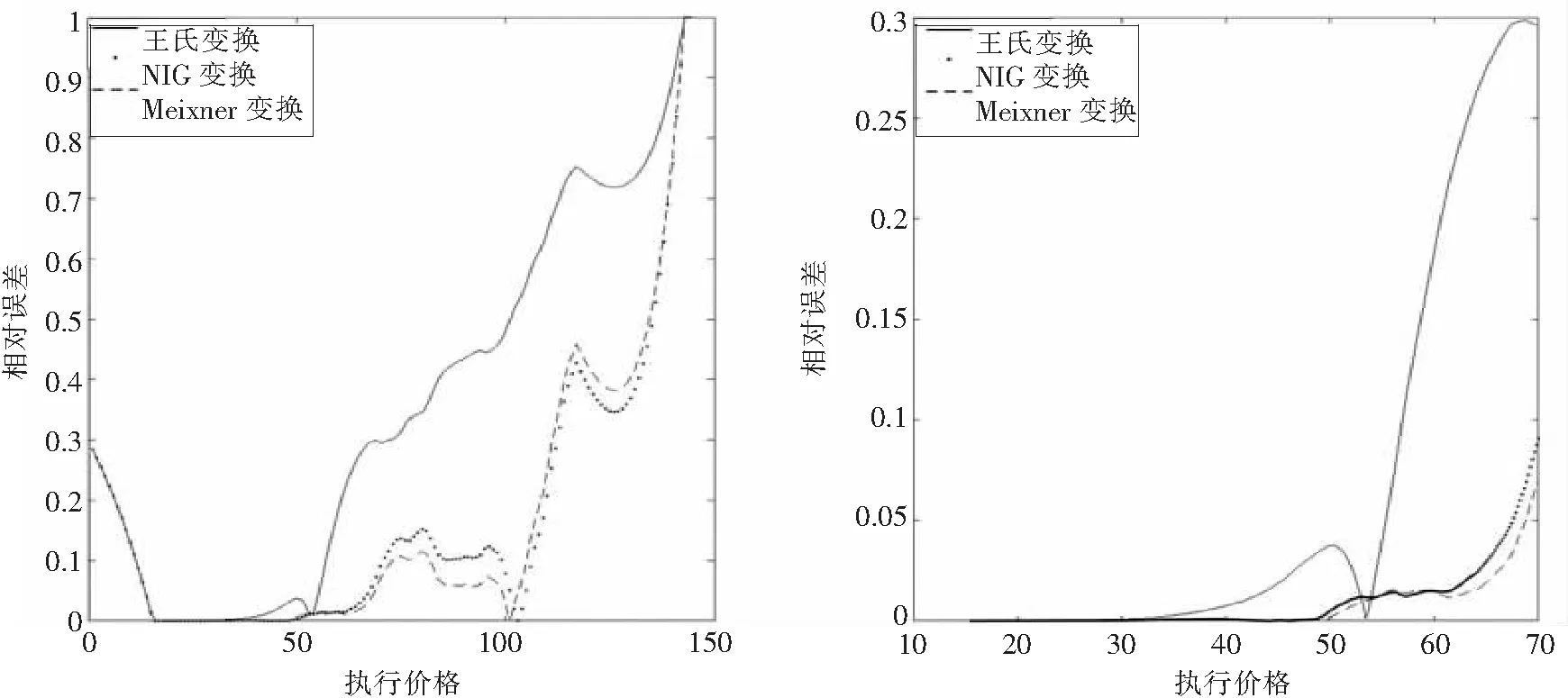
图4 Meixner模型中三种扭曲算子价格的相对误差Fig.4 The relative errors of prices of three distortion operators in Meixner model

4.5 VG模型

设模型(7)中的Xt是参数为(θ,ν,σ,μ)的VG过程. 取参数S0=50,r=0.05,

T=0.5,θ=-0.2,v=0.1,σ=0.15,μ=0.15后, 模拟出5 000个股票价格XT. 利用模拟价格, 分别得到NIG分布和Meixner分布参数的极大似然估计值为

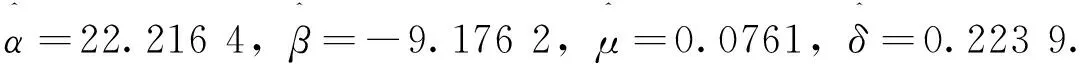
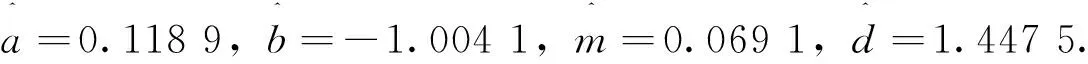
本次模拟max{ST}=138.144 9,min{ST}=15.637 0, 从图5左图可以看到, 当执行价格 不小于138.144 9时, 三种扭曲函数得到的相对误差都为1; 当执行价格K→0+时, 三种扭曲函数得到的相对误差都收敛于exp(-rT)min{ST}/S0=0.305 0. 从图5右图可以看到, 总体上来说, NIG价格和Meixner价格比较准确, 王氏变换价格比较差.

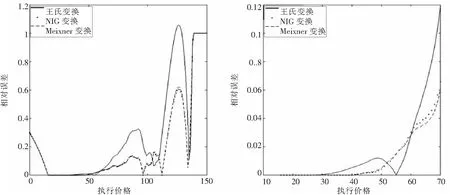
图5 VG模型中三种扭曲算子价格的相对误差Fig.5 The relative errors of prices of three distortion operators in VG model