高转速、大容量卧式水轮发电机组关键技术分析研究
2022-10-03周一飞
周一飞
(杭州杭发发电设备有限公司,杭州 310018)
0 引言
水轮机、发电机是水力发电设备系统中的两大关键设备,水轮机将水的势能转化为机械能,发电机将机械能转变为电能。2021年是“十四五”规划开局之年和碳中和元年,水电清洁能源开发有着广阔的发展前景,水电装备技术将进一步创新突破,朝着高水头、高转速、大容量和高可靠性发展。因此高水头、高转速和大容量水轮发电机组关键技术的研究:通风冷却系统流场和温度场耦合的数据计算技术、高转速、内循环滑动轴承多目标优化技术、基于遗传算法的滑动轴承优化设计技术是目前十分迫切的任务。
本项目的研究区别于其他对高水头、高转速、大容量水电机组的研究,采用耦合求解的方法为水轮发电机定子寻找了高效、合理的通风思路,并借助遗传算法解决滑动轴承的多目标优化问题,从而推广电站的低能耗配置。同时借助有限元对机组的稳态性能进行分析,较传统计算更贴切真实值。
1 滑动轴承流体动力润滑分析
1.1 轴承油膜热流耦合分析
以SFW2-J1000-8/1180型水轮发电机组的径向轴承为研究对象,油膜模型是按照φ220轴承设计图纸及轴承润滑计算偏心率数值建立的,其进油口在+Y偏+X轴上方25度,取轴向3mm宽油膜模型作为计算域,对油膜进行稳态CFD分析,材料采用L-TSA-46油,如图1所示。

图1 油膜网格图
模拟假定油膜为无限宽,润滑油假设为不可压缩,且其各点粘度相等,形成油膜重量假设为忽略不计,油膜运动惯性力忽略不计,其边界条件有:
1)压力进口,为保证供油充足进油压力取0.001MPa;
2)压力出口,取油膜出口面为开口流;
3)边界流动面,取油膜内外圆面;
4)流域面,取油膜内外圆面;
5)对称面,取油膜两端面;
6)油膜内表面应施加750r/min的旋转框。
1.1.1 CFD分析计算
根据上述基本假设和给定边界条件,解算得到轴承油膜的静压与温度分布云图,如图2和图3所示。

图2 油膜静压云图

图3 油膜温度云图
由上图可知最高压力为3.296MPa,油膜温度区间为49℃至52.36℃,轴承油膜温度分布在供油充足情况下,在许用范围内。对比表1中实测油温结果和CFD计算结果(表中数据为实际温度)。

表1 轴承油膜温度对比
从上述计算中可看到:通过求解后的压力场和温度场分布结果,在供油充足情况下,进油口位置在+Y偏+X轴25度方向,上瓦设有4mm深周向油槽的轴瓦,设计是合理的,油膜容易形成、油膜温度低。模拟值与实测值非常接近,证明了模拟的准确性及可行性。
1.2 计入轴颈倾斜的滑动轴承流体动力润滑分析
实际情况下,径向滑动轴承工作时,轴颈多处于倾斜状态,在轴承润滑分析中考虑到轴颈倾斜,要获得轴承压力分布和静态特征,需要进行步骤较多的多次迭代和复杂的循环求解。通过Reynolds方程使用Matlab编程计算求解,滑动轴承流体动力润滑分析计算流程如图4所示。

图4 滑动轴承流体动力润滑分析计算流程
1.2.1 仿真润滑分析结果
1.2.1.1 轴颈不倾斜润滑分析
仿真润滑分析结果如图5和图6。

图5 油膜厚度分布图
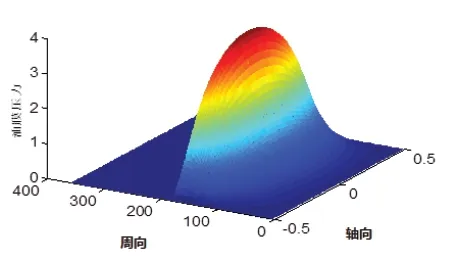
图6 油膜压力分布图
分析分布图,得出结论如下:
1)轴承油膜厚度沿周向展开是余弦函数,轴承油膜厚度逐渐减小直至最小厚度再逐渐增大,沿轴向厚度均匀不变,整个油膜只存在一个楔形。
2)轴承油膜压力沿周向先增大到达最大极值后减小,沿整个周向呈非线性分布。油膜压力沿轴向呈抛物线分布,整体来看,油膜压力最大值位于轴承宽度中央。
1.2.1.2 轴颈倾斜润滑分析(α=0°)
考虑轴颈倾斜方位α=0°时,不同轴颈倾斜角对轴承润滑性能的影响。
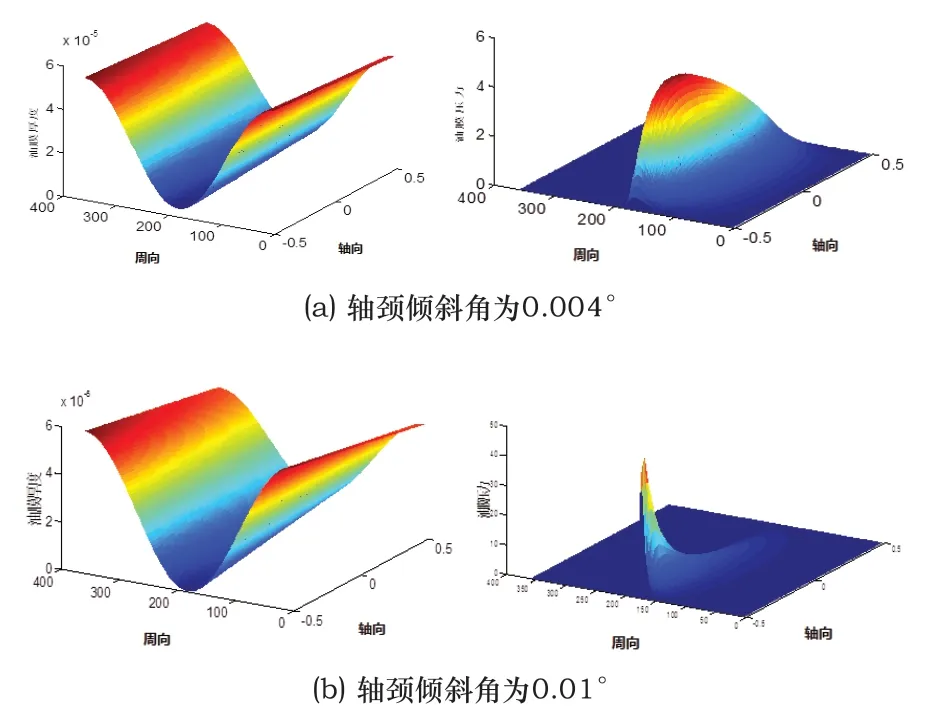
图7 轴承在不同轴颈倾斜角时的油膜厚度和油膜压力(α=0°)
轴颈倾斜方位α=0°时,对比轴颈不倾斜分析,结论如下:
1)油膜压力和油膜厚度呈现分布不同情况,两者分布差异随倾斜角增加而增大。
2)油膜压力最大值位置发生移动,移向轴承一端的端部,随着倾斜角的增加,油膜压力最大值位置越接近端部。
3)倾斜角增至最大时,油膜压力呈现单峰分布,压力最高值比轴颈不倾斜时增加了数倍。
1.2.1.3 轴颈倾斜润滑分析(α=90°)
考虑轴颈倾斜方位α=90°时,不同轴颈倾斜角对轴承润滑性能的影响。

图8 轴承在不同轴颈倾斜角时的油膜厚度和油膜压力(α=90°)
轴颈倾斜方位α=90°时,对比轴颈不倾斜分析,结论如下:
1)油膜压力分布状况发生了明显变化:倾斜角增加,油膜压力随倾斜角增大而向两端端部移动,当倾斜角增大到最大值时,油膜压力分布出现双峰,且压力值也成倍增加。
2)油膜厚度分布状况发生了改变:轴颈倾斜时,油膜厚度值各不相同,呈现最小油膜厚度,位置在轴承一端的端部,最小油膜厚度值随轴颈倾斜角增大而减小。
1.3 基于通用膜厚的动压轴承形状优化
1.3.1 优化模型
动压轴承的形状优化模型可用如式(1)所示:
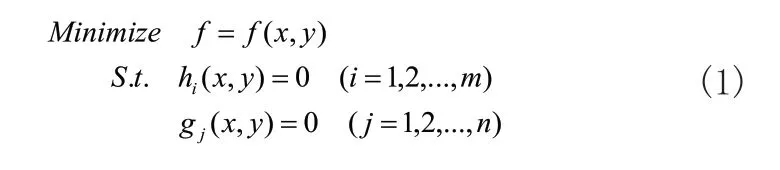
基于软件MATLAB语言结合编程,对动压轴承的形状优化模型进行求解。MATLAB PDE有限元数值求解框图如图9所示。

图9 MATLAB PDE有限元数值求解框图
上述动压轴承膜厚泛函方程采用遗传算法、MATLAB求解优化模型,以动压轴承获得承压最大的优化结果和轴承型线函数为目标。
1.3.2 优化分析
设l/d=1和Tol=10-2,计算n取1,2,3时的值,承载力和设计变量如表2所示。
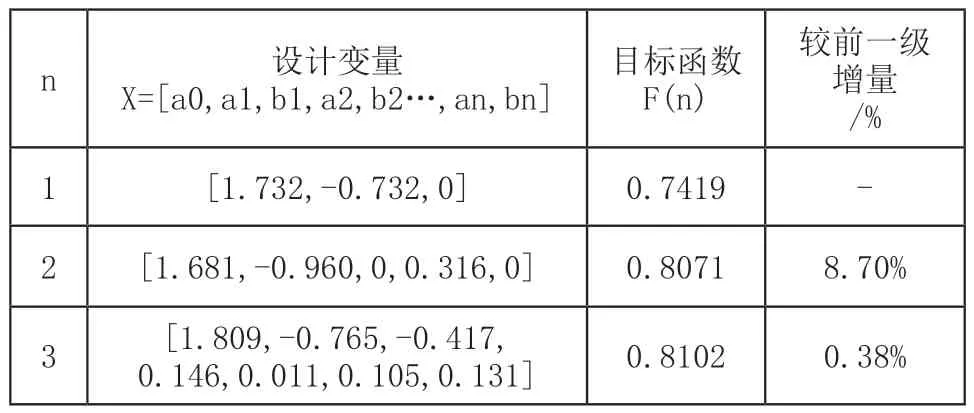
表2 不同级数n对应的优化结果
从表2中看出,n值越大,优化结果越好,但n值不宜取太大,否则计算量过大。通过采用逐步逼近法确定n值,使无穷级数变为可确定值。由计算结果对比可知,n=2时迭代已收敛,n继续增大时优化效果越来越不明显。
图10显示了选用不同的级数n所优化的轴承型线图。蓝色实线为原圆轴承轮廓线,不同颜色虚线分别表示不同级数n下的优化型线轮廓,相比于原先的圆轴承,优化后的轴承形状为近圆形。
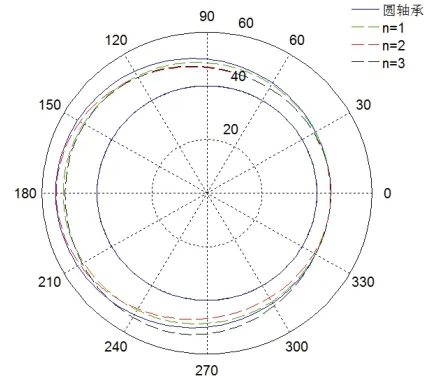
图10 轴承型线截面图
不同级数对应的轴承型线沿周向的展开如图11所示,不同级数对应的型线均仅有一个楔形收敛区,且轴承的总承载力较高。

图11 轴承型线展开图
根据图12不同级数n对应的轴承压力分布图可以看出,由于不同级数n所优化的轴承型线不同,轴承油楔形状也不同,使无量纲压力分布及最大比压力值也不同,n=2时的无量纲压力大于n=1时的值,说明级数为2时的轴承最大承载力最优。
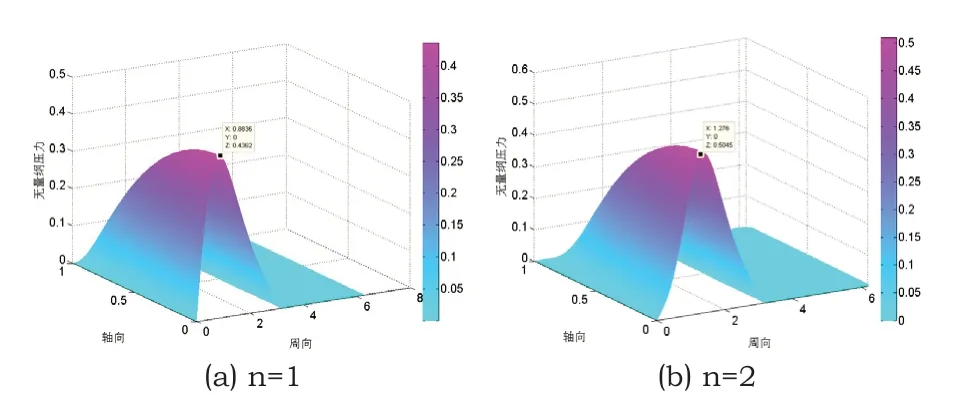
图12 当级数n分别为1和2时对应的比压分布图
综上,通过优化,轴承的最大承载力提高了8.7%,确保形状全局优化、轴承承载稳定、机组运行安全可靠。
2 通风冷却系统结构的计算机流场分析
以SFW-J5000-4/1480型水轮发电机通风系统为例如图13所示,根据电站实测数据来看,这台发电机的风量过大,故对该机型通风系统进行优化设计,使用NX THERMAL/FLOW进行有限元分析。
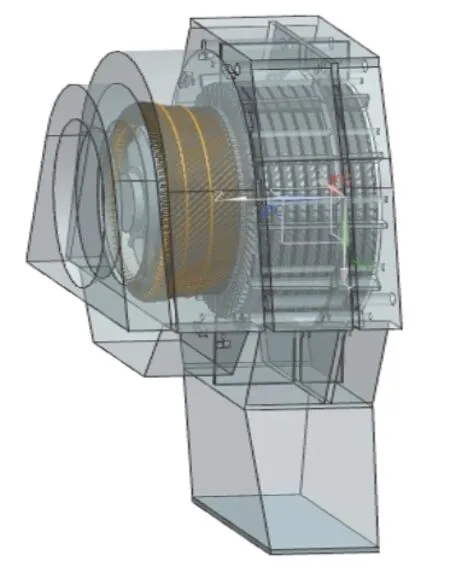
图13 1/2通风系统流体域模型
2.1 通风系统仿真的边界条件
1)进出口为开口流。
2)模型1/2对称处设为对称面。
3)定转子空气域网格。
4)空气流动面;壁摩擦设为光滑-有摩擦,无滑动壁。
5)移动旋转框旋转转速为额定转速1500r/min。
2.2 有限元解算结果
模拟结果进出口平均风速分别为4.78m/s、2.47m/s;进出口面积分别为:0.4m2、0.78m2。那么,进出口风量分别为:1.91m3/s、1.93m3/s。进出口风量差别很小,说明通风系统内部空气流动比较流畅,但端部冷却较果不是太好。从放大图看,端部风速与铁心中心风速有明显差别,而且有旋涡现象。定子铁心轴向风速分布如图14所示,可看出端部风速比铁心风速小很多,铁心段风速比较均匀。

图14 通风系统流线图
电机损耗所需散热量为109kW,通风系统所需用风量为2.02(m3/s),电站实测风量进口为2.86m3/s,出口风量为2.55m3/s。由此看来裕量是很大的,有必要进行优化。
发电机通风系统目的是有效的带走电机中损耗热量,使电机运行在允许的温度范围内。从单位流量的通风损耗减小及结构简单、运行可靠、维护加工方便方面考虑,将风扇叶片数减少为三个,模拟结果得进出口风量分别为:1.98m3/s、1.99m3/s。
通风系统不同结构时的模拟风量与实测风量比对如表3所示。

表3 模拟与实测通风量对比表
由上表数据看出如果在有空冷器情况下,通过对风扇结构的重新设计,使得通风系统结构更简洁,风量增加,且3个风扇叶比9个风扇叶端部散热性更好。
3 高效稳定转轮的设计分析
本项目以公司某水轮机产品为例进行内部流体流动状况研究,基于UGSNX平台,对水轮机各部件的过流区域建模,基于ICEM对各几何模型进行网格划分,基于FLUENT进行数值计算。为观测尾水管流域存在的非稳态的压力脉动现象,釆用非稳态模型研究尾水管流域的流动变化,分析水轮机内流道的流动状况,为后续结合实际水轮机运行状况作前期的测试与探索。
3.1 混流式水轮机全流道几何模型的建立与网格划分
本次研究基于UGS NX平台,各过流部件三维建模,获得的流场域。再使用ICEM对模型进行网格划分如图15所示。

图15 混流式水轮机网格
3.2 全流道非稳态数值模拟研究
水轮机在运行过程中,流体运动在固体边界会存在变形情况,本项目基于滑移网格(Sliding Mesh)模型,进行全流道非稳态数值模拟,重点对尾水管直管段流域流体的瞬时变化状况进行研究与分析。
3.2.1 计算结果分析
3.2.1.1 最优开度
在尾水管入口处安装2个监测点A点和B点,如图16所示。
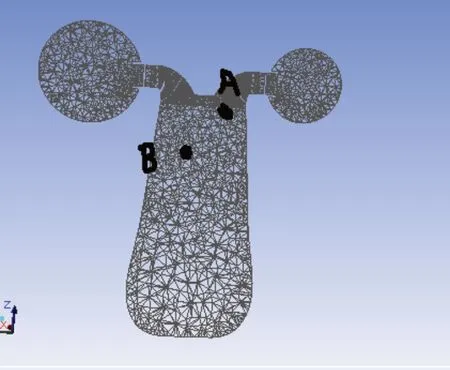
图16 尾水管压力监测点公分布图
A点:监测测量尾水管入口段壁面压力。
B点:监测测量锥管段中心轴附近压力。点锥
初次采用最优开度进行计算,分析测得的压力脉动曲线可知A点处压力随时间变化相对稳定,如图17所示,根据流体迹线未发现明显漩涡。压力脉动的赋值也比较小,看不出涡动,机组运行状态良好。

图17 压力脉动检测图
3.2.1.2 非最优开度
当开度在5~13范围时监测点均监测出压力脉动,以开度8为例模拟结果,如图18所示。
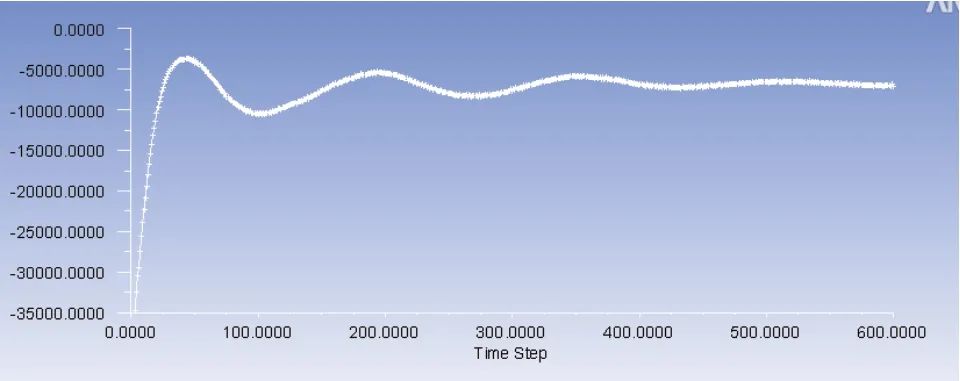
图18 观测点B压力变化图
结果显示,约在0.2s后,上游旋转流开始对尾水管直管段流场产生影响,B点处压力随时间发生显著波动,幅度与周期均有明显变化,由此可知,尾水管的流场存在着强烈的扰动。
获取一横截面的压力随时间变化分布图,如图19所示,受转轮旋转影响,存在涡动,各截面分析如下:

图19 尾水直锥管四个截面压力分布图
1)全时间段内截面中心出现大小不同的低压区。
2)低压区均为偏心旋转。
3)压力偏心旋转有一定的相位差。
综上所述,通过上述分析方法,获得尾水管入口处的压力变化和分布情况,直观地显示出压力脉动是导致尾水管振动的直接原因。减小甚至消除水轮机尾水管内压力脉动是避免机组运行时发生低频共振的重要手段。
4 结语
本项目对高转速、大容量水轮发电机组的这几项关键技术的研究取得了突破性研究成果。首先,采用热流耦合计算高速轴承运作产生的温度场,预测轴承油膜是否失效,并且用泛函数形状优化对轴承进行优化。其次,通过对通风冷却系统结构的计算及流场分析,有效地控制高转速工况下电机的温度。最后,通过分析不同导叶开度下引起的尾水管压力脉动情况,避免整机发生低频共振。这些研究成果对以后对高转速、大容量水轮发电机组的探索与研究提供了理论依据。
