基于机器视觉的小模数齿轮精度参数自动化检测技术研究
2022-10-03袁鹏哲张启元张烈山
袁鹏哲,张启元,陈 莉,余 箫,张烈山
(浙江理工大学 机械与自动控制学院,杭州 310018)
0 引言
齿轮是一种传递运动和动力的机械零部件,是机械产品中重要的基础元件,其广泛应用于汽车车辆、电动工具、航天航空、各类机械设备等众多主机行业[1]。
齿轮是机器中质量最大、最复杂、最关键的零件之一,在很大程度上决定了所使用的机器和机构的性能[2]。作为传动系统的核心部件,传动系统的质量往往由齿轮的精度决定。国家标准GB/T10095.1-2008和GB/T10095.2-2008对渐开线圆柱齿轮的精度参数进行了明确的规定。对齿轮精度参数的精密测量是保证其互换性、连接强度、工作精度等性能的基本前提,因此实现齿轮精度参数的自动检测对提高齿轮的传动精度和可靠性具有非常重要的意义[3,4]。
小模数齿轮是指模数小于等于1mm的齿轮,一般来说其外形尺寸也比较小,广泛应用于精密机械、仪器仪表等精密传动领域。传统的综合性齿轮测量仪器如CNC齿轮测量中心、三坐标测量机存在操作复杂、价格昂贵、维修难度大、适应性较差、动态性能不足、效率低下等问题,无法进行在线的应用[5~11]。而专用的齿轮测量器具,例如公法线千分尺、游标测齿卡尺等都只能实现某一项精度参数的手工测量,测量效率和精度都受到很大限制。这两类方法都属于接触式的离线测量方法,受到探头尺寸的限制,它们无法伸入小模数齿轮的齿槽内,进而无法实现其精度参数的检测。
进入新世纪以来,在制造业中信息化、智能化的发展趋势越来越要求质量检测技术具备较低的时延,能够实现产品在位检测。机器视觉影像测量技术正是这样一种高效的检测方法,它是一种融合了计算机图形学、信息处理、光电子学和模式识别等科学为一体的现代检测技术,具有非接触、高速度、动态范围大、信息量丰富、成本相对低廉等诸多优点,广泛用于各种实时、在线、自动化的精密测量中[12~15]。
机器视觉检测技术作为一种高效的几何量测量新技术,也非常适用于小模数圆柱直齿轮精度参数的测量。特别是智能制造大背景下,如何实现齿轮精度参数的自动化、非接触、高精度检测成为齿轮制造智能化的基础性问题。本文将影像测量技术应用在小模数齿轮精度参数的自动化检测上,搭建了一套小模数圆柱直齿轮精度参数测量实验系统,对本文所述方法进行了实验验证。
1 齿轮精度参数检测原理
机器视觉齿轮精度参数检测系统的原理如图1所示,它通过成像系统将被测物面成像至光电检测单元(相机感光面),光电检测单元将光信号转换为电信号(电子图片),并将其传送至上位机。上位机获得检测图像后,利用图像处理软件从检测图像中提取出所需的几何特征,在根据成像系统的数学模型,计算出所关心的几何量,从而实现被测产品几何参数的测量。
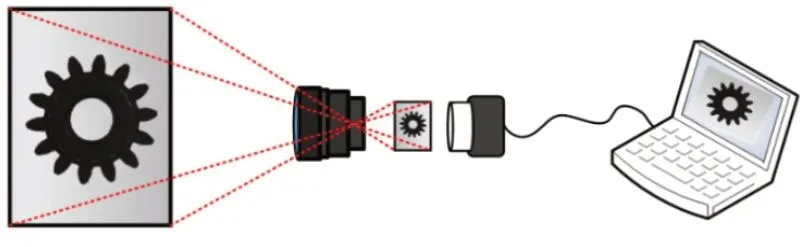
图1 测量系统原理示意图
1.1 坐标转换原理
为了建立测量模型,引入了4个坐标系:
1)世界坐标系Ow-XwYwZw,也称为测量坐标系用于描述被测物体的空间位置;
2)相机坐标系Oc-XcYcZc,也是一个三维直角坐标系,原点位于镜头光心处,X、Y轴分别与相面的两边平行,Z轴为镜头光轴,与像平面垂直;
3)像素坐标系O0-UV,一个二维直角坐标系,反映了相机CCD/CMOS芯片中像素的排列情况。原点位于图像的左上角,U轴、V轴分别与像面的两边平行,其坐标值为整数,单位为像素;
4)像平面坐标系O-XY,又被成为图像坐标系,是一个二维直角坐标系,其坐标轴的单位通常为毫米(mm),原点是相机光轴与相面的交点(称为主点),即图像的中心点,X轴、Y轴分别与U轴、V轴平行。可由像素坐标系经过平移和单位变换得到图像坐标系。
机器视觉一般测量过程就是从获得的检测图像中提取出特征点(或点族),经过一系列坐标变换得到世界坐标系下被测物体的特征点坐标,进而得到被测物体各项几何参数。因此,机器视觉测量过程的关键是坐标系的转换。对于单目视觉测量来说,为了方便计算,选定世界坐标系的X轴、Y轴分别与相机坐标系的X轴、Y轴平行,坐标原点则设计为成像系统光轴与被摄物平面的交点。因此,本文所述方法所涉及到4个坐标系的关系如图2所示。

图2 视觉检测系统坐标系关系示意图
图像坐标系与像素坐标系的关系为单位转换和坐标平移的关系,设像素坐标系原点在像平面坐标系下的坐标为(u0,v0),每个像素点在图像坐标系x轴、y轴方向的尺寸为dx和dy,且像点在像平面坐标系下的坐标为(x,y),于是可得到像点在像素坐标系下的坐标(u,v)的齐次坐标形式如式(1)所示:

本文所设定的世界坐标系与相机坐标系的关系特殊,仅存在坐标的平移,设被测物面上某点的坐标为(xw,yw,0),其对应在相机坐标系下在坐标为(xc,yc,U)因此可得两个坐标系的转换关系为:

式(2)中,U为被测物面到镜头光心的距离,也即物距。
从相机坐标系到图像坐标系的转换就是3D坐标点到2D平面的透视映射。根据小孔成像模型和三角形相似定理可以得到两个坐标系的转换关系为:

式(3)中,f为镜头的有效焦距,单位:mm。
联合式(1)~式(3),最终整理可得像素坐标与世界坐标系的转换关系:

式(5)中,fx为U轴方向归一化焦距,fx=f/dx;fy为V轴方向归一化焦距,fy=f/dy。
这样就能将像素坐标系中所有的点转化到被测物面坐标系,也即世界坐标系。单目视觉测量中,提取出来的特征点将其转换到世界坐标系下,即可得到实际被测物体的几何尺寸信息。
1.2 相机标定及图像矫正
由相机获取的图像上每一点的亮度将反映空间物体表面某点反射光的强度,而该点在图像上的位置则与空间物体相应点的几何位置有关。这些位置的相互关系由相机成像几何模型所决定。该模型的参数称为相机参数,这些参数必须由实验与计算来确定,实验与计算的过程称为相机标定。式(5)中的fx,fy,u0,v0均为本文相机标定过程中需要确定的内参数,物距U为外参数。
在理想情况下从相机坐标系转换到图像坐标系时,放大倍率是常数,但是在实际的光学系统中,透镜的放大率会随光束和主轴间所成角度改变而改变。由于透镜制作和安装存在不确定性,导致远光轴区域的放大率与光轴附近的放大率差异较大时会导致平面内图形的各部分与原物不成比例,这种现象就是图像畸变,常见的图像畸变又分为径向畸变和切向畸变两种。本文引用张正友标定法[16,17],利用标准棋盘格实现内参矩阵和径向畸变、切向畸变参数的标定及矫正。
式(5)中U/fx和U/fy被称为系统的像素当量,单位为:mm/pixels。由于标定用标准棋盘格的方格边长为已知标准量,根据标定图片可知一个方格边长所占据的像素数,两数相除即可得到像素当量,进而可得物距U。
1.3 图像预处理
利用成像系统和相机采集的被测物数字图像往往包含一些噪声,而且被测物的特征也很不明显。因此,完成被测齿轮图像采集后,必须对图像进行预处理,完成齿轮轮廓边缘的提取。
数字图像的预处理主要包括高斯滤波、二值化、腐蚀膨胀以及Canny边缘提取四大部分。高斯滤波可以有效地消除实际相机拍摄图像中出现的高频噪声干扰。图像二值化使处理后图像的灰度值只有0和255两种数值,从而保留和突出重要的形态信息。通过腐蚀和膨胀对二值图中的高亮区域进行处理,则可以使得目标轮廓边界更为平滑,便于后续处理。Canny算法通过梯度算子计算突出灰度值,并对得到的图像进行强度梯度筛选、非极大值抑制、双阈值算法等运算,保证边缘提取准确率。
1.4 测量算法流程
完成齿轮图像的预处理后,基本上得到了齿轮的内外轮廓,如何从外轮廓像素中提取出有用特征,是最终实现齿轮几何参数自动化测量的关键。本文以小模数圆柱直齿轮的齿距、齿厚和公法线长度3个重要的齿轮制造精度控制参数的自动测量为例,设计了机器视觉测量算法,具体流程图如图3所示。

图3 测量算法流程图
完成图像预处理后,需要对外部齿廓像素进行进一步处理,从中提取出齿廓中齿顶圆像素点,再利用最小二乘法拟合齿顶圆。其中,提取齿顶圆像素点这一关键步骤尤为重要,直接影响着测量系统的整体精度,其算法流程图如图4所示。首先应用OpenCV中的Findcontours()函数从预处理后的图像中提取出齿轮的内外轮廓像素,并抠除齿轮的安装孔轮廓;然后利用最小凸包算法勾勒出齿轮最外层轮廓,并以5×5的大小建立齿顶圆掩膜;最后将预处理后的图像与掩膜相乘,便得到齿顶圆轮廓。

图4 齿顶圆像素点提取算法流程图
齿根圆像素点的提取过程如图5所示,先计算齿顶圆的像素圆度,也即先评估齿顶圆上点相对于理想圆的径向波动范围,记为ΔR;齿根圆和齿顶圆同心,再计算齿廓上离圆心最近的点(该点必为齿根圆上点),记录该点到圆心的距离为Rmin;齿根圆与齿顶圆应具有相当的圆度误差,判断每一个齿廓上的像素点到圆心的距离是否小于(Rmin+ΔR),若小于该值则该像素点记为齿根圆上点。
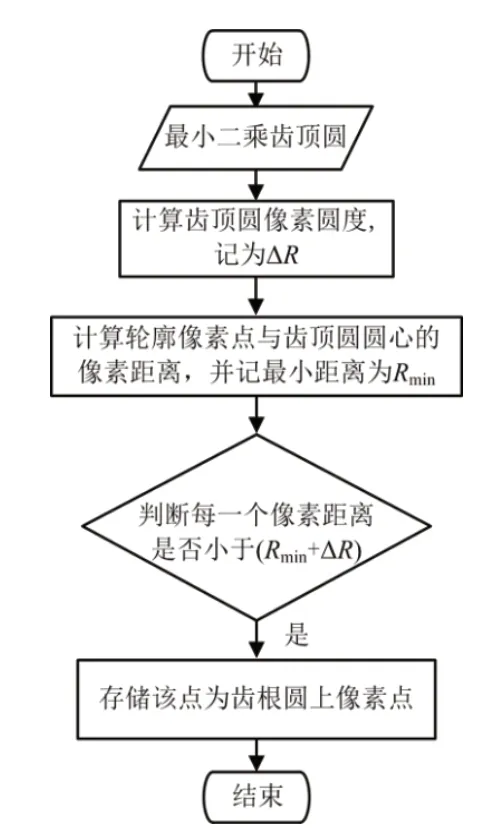
图5 齿根圆像素点提取算法流程图
除了齿顶圆和齿根圆像素点的提取以外,本文所述齿轮参数自动测量算法的3个关键子程序分别为:圆的最小二乘拟合算法、测量点提取算法以及精度参数计算算法,下面将简述这3个关键子算法的原理。
1.4.1 圆的最小二乘拟合
本文使用最小二乘法原理拟合齿顶圆、齿根圆。最小二乘法是从误差拟合角度对回归模型进行参数估计的方法,它通过最小化误差的平方和寻找数据的最佳函数匹配。
设拟合圆的面积为S,圆心为(a,b),半径为r。通过Canny算子边缘检测得到的第i个边界为D(xi,yi),i∈(1,…,n),该点距离圆心的距离为ri,以ri为半径的圆面积为Si,那么两个圆的面积误差εi为:
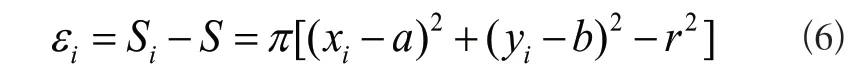
根据最小二乘原理,当误差εi的平方和最小时,解得:
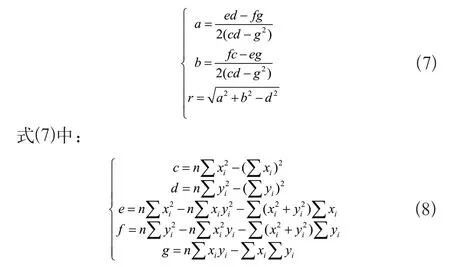
1.4.2 测量点提取
对于测量点的确定,根据齿轮几何参数的定义本文先在齿轮外轮廓图片上构造与齿轮基准轴线同心参考圆,参考圆与齿轮外轮廓的交点即为测量点。不同的被测参数具有不一样的参考圆(详见1.4.3节),测量点定义如图6所示。利用图3所示算法已经拟合得到的齿顶圆和齿根圆,参考圆与它们同心,直径则是根据它们各自的定义得到,这样很容易在软件算法上实现各个参考圆的构建。
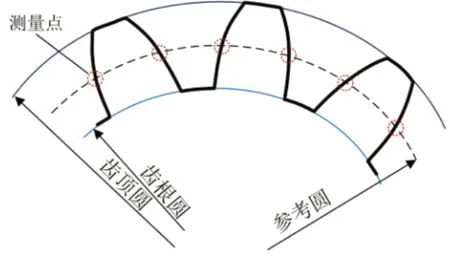
图6 测量点示意图
1.4.3 齿轮精度参数计算
小模数齿轮主要用于精密传动结构中,它对传动的准确性有较高的要求。齿轮精度参数中,齿距偏差、齿厚、公法线长度等参数是影响传动准确性的主要因素,因此本文主要针对小模数齿轮的齿距,弦齿厚及公法线长度(如图7所示)进行检测。这些参数的定义均为两测量点间的弦长或者弧长,因此只需要明确两测量点的位置坐标与齿轮中心坐标即可。算法实现过程中,需先构造参考圆或者切线,然后提取测量点,将测量点像素坐标转换到物平面坐标系下,然后计算两个测量点的距离或者弧长即可实现齿轮几何参数的计算。

图7 齿轮几何参数定义示意图
1)弦齿厚的测量算法
弦齿厚定义为齿高中部圆圆周上一个轮齿两侧齿廓间弧线的弦长就是齿厚,如图7中Si所示,也即图中测量点c和d之间齿中圆圆弧的弦长。构造齿中圆之前,需拟合齿顶圆和齿根圆,得到齿顶圆和齿根圆的直径和圆心,齿中圆的直径即为齿顶圆和齿根圆直径的平均值,其圆心与齿顶圆和齿根圆同心。通过计算每齿与齿中圆的一对交点间的距离即可得到弦齿厚,其计算公式简单在此不予赘述。
2)齿距的测量算法
根据定义,齿距定义为分度圆上任意两个同侧齿面间的弧长,如图7中P所示,也即图中测量点a和b之间的分度圆圆弧。通过计算相邻两齿与齿中圆的两对测量点中两个同侧测量点间的弧长获得。要构造分度圆,需要先计算得到该齿轮齿数Z,分度圆与齿顶圆同心,其直径则为模数m(模数采用其规格值)和齿数Z的乘积。在齿厚参数的计算前,先构造了齿中圆提取了齿中圆上的各个测点。根据测量点的个数能够计算出该齿轮的齿数Z。
构造分度圆后,提取测量点a和b,再结合分度圆的圆心坐标,可根据式(9)来计算齿距P:
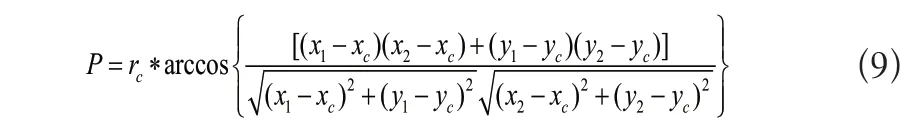
式(9)中,(x1,y1)和(x2,y2)为物平面坐标系下两个测量点的坐标,(xc,yc)为物平面坐标系下分度圆圆心的坐标,rc表示分度圆的半径。
3)公法线长度的测量算法
公法线长度是指齿轮上几个轮齿的两端异向齿廓间所包含的一段基圆圆弧的弦长,即该两端异向齿廓间基圆切线线段的长度如图7中Wk所示,也即测量点e和f之间的线段长度,以图7所示跨齿数k=3为例,公法线长度的计算过程如下:
(1)根据定义基圆与分度圆同心,基圆直径等于cosα与分度圆直径的乘积,α为压力角,由此构建基圆,记圆心为O;
(2)构建测量c和测量点d的中心点,记为点O’;
(3)连接圆心点O和中心点O’,构建中心线OO’;
(4)计算中心线OO’与基圆的切点坐标;
(5)根据切点构建基圆的切线,切线的方向与中心线OO’正交;
(6)提取切线与齿轮齿廓的交点,即为图7中测量点e和f;
(7)计算测量点e和f之间的距离,即为所求公法线长度W3。
2 小模数齿轮精度参数测量实验
2.1 实验系统
为验证本文所述机器视觉方法测量小模数圆柱直齿轮精度参数的有效性,搭建了一套影像测量系统。为模拟实际自动化生产线,实验系统通过传送带传送齿轮到指定位置。将影像测量系统安装到工业机器人的末端,利用上位机控制机器人调整相机拍摄位置与拍摄角度。该系统实物如图8所示,它主要由传送带、机械臂、LED光源、定焦镜头、工业相机以及上位机所构成。该系统里有COMS高分辨率工业相机进行摄像,将获取的图像上传至上位机,进行图像处理和参数测量计算。测量系统主要部件的型号及性能参数如表1所示,系统尺寸测量分辨率为0.006mm。

图8 系统图像采集实物图

表1 测量系统主要性能参数
2.2 齿轮参数测量
本文对精密传动领域常用的14齿小模数直齿轮进行一系列齿轮参数测量实验。为了验证本文所述方法和系统的准确性,使用标准14齿小模数齿轮作为被测件,其主要几何参数如表2所示。

表2 待测件规格参数
2.3 测量结果分析
对齿轮图像进行处理后,可以得到如图9所示的外部齿廓图像。再由外向内分别构建分度圆、中圆以及基圆,从它们与齿轮轮廓构成的相交图像中提取测量点,并画出如图10所示的公法线图像,最终通过测量算法算出齿轮的齿厚、齿距和公法线长度。

图9 被测齿轮外部齿廓图

图10 公法线实际测量模型构建图
2.3.1 测量重复性分析
使用本系统对待测件上同一齿进行8次测量,再对数据进行比较,可得到测量重复性的分析结果,待测件测量参数如表3所示。

表3 重复性测试实验结果 (单位:mm)
由表3测量结果,运用贝塞尔公式进行重复性标准差的计算,可以得出三项齿轮参数测量结果的重复性标准差均小于等于0.013mm,以齿距的重复性测试为例,作出图11所示折线图,可以清晰的判断出该测试齿序的齿距在1.847mm~1.878mm之间,可见本系统的测量重复性较高。

图11 齿距重复性测试折线图
2.3.2 测量正确性分析
同样本文还对待测件进行多次测量后求和取平均值。由于被测齿轮精度参数的真值未知,故这里将测量结果与被测齿轮规格参数进行对比,以检验本系统测量结果的正确性,被测件测量平均值与偏差如表4所示。

表4 正确性测试实验结果 (单位:mm)
从表4中反映的是对齿轮14个齿序的齿厚、齿距以及分别14个齿序为基准的三齿公法线长度,以齿轮齿厚为例,作出如图12所示的折线图,比较直观的展示出齿轮的齿厚情况,可以看出,齿轮齿厚、齿距、公法线长度与齿轮规格参数偏差最大仅有0.002mm,可见本系统的测量重复性精度极高,测量所得结果具有很高的正确性。

图12 齿厚测量结果折线图
3 结语
针对的小模数圆柱直齿轮的精度参数测量问题,本文提出了一种基于机器视觉的自动化检测方案。该方法利用高分辨率工业相机和成像系统对被测小模数齿轮进行摄像,经图像预处理、齿轮特征拟合、测量点提取、坐标转换等处理后,根据齿轮精度参数定义计算出被测齿轮的精度参数值。从测量结果及分析看,该自动化测量系统的测量重复性良好,测量标准差达0.013mm,重复性精度较传统方法更优。本文所述方法和系统实现了对小模数齿轮各精度参数的非接触、高精度的快速检测。解决了当前接触式测量法因探头尺寸限制无法实现小模数齿轮精度参数测量的问题,为齿轮的自动化在线检测提供了可行的技术方案。
