黏粒含量对钙质砂渗透特性影响试验研究

2022-10-02朱学敏庞志明代佳骏肖昕迪

辽宁科技学院学报 2022年4期

朱学敏，庞志明，代佳骏，马露，于敏，肖昕迪

(安徽科技学院建筑学院，安徽蚌埠 233000)

1 概述

最近几十年我国近海工程数量增长迅速，而此类工程面临的最大难题是沿海地区土质复杂，土体性质受海水影响较大。本文针对我国南海地区土质进行研究，南海海域钙质砂分布广泛，土体中黏粒含量较高，前人主要基于钙质砂的理化特征和力学性质进行研究，对其渗透特性的研究不足。钙质砂内空隙较多，棱角突出且易破碎，其主要成分是碳酸盐，其中CaCO3含量超过90%，且夹杂各种海洋生物[1-2]。渗透系数的确定一般有室内试验和理论计算两种方法。室内试验方法分为常水头试验和变水头试验，且试验过程较为烦琐，同时试验人员的操作熟悉程度对试验数据影响较大，因此仅通过试验的方法确定渗透系数会产生一定误差。本文通过数据分析并拟合提出一种经验公式，旨在建立一种可解决实际工程问题的渗透系数计算方法。

渗透特性是土体的一个重要性质，国内外学者对此研究较为广泛。1856年Darcy通过室内试验研究提出均质砂土在层流情况下流速v与渗透系数k和水力坡降i的关系公式v=ki[3]，但此公式仅针对无黏性土层流下的工况，适用情况受限；随着进一步研究，相继有Terzaghi[4]公式、Hazen[5]公式、朱崇辉[6]公式和苏立君[7]公式建立了各种不同因素与渗透系数的相关关系，但上述公式适用情况各异；胡明鉴等[7]发现渗透系数与不均匀系数呈现负相关关系，而苏立君等[8]认为渗透系数与不均匀系数呈正相关性，并研究了渗透系数随孔隙率、颗粒粒径和曲率系数的变化规律，试验结果显示渗透系数与上述影响因素呈现较好线性相关关系。在试验基础上建立了渗透系数经验公式，并与前人计算公式对比，发现该计算公式具有较高的可靠性，但缺乏针对黏性土渗透特性的研究；钱琨等[9]通过室内试验研究了钙质砂颗粒级配和孔隙比与渗透系数的关系，并经过综合分析得到渗透系数计算公式。发现该计算公式与前人计算公式相比精度有较大提高，但该计算公式仅能反映钙质砂的渗透特性，对于混合土层渗透系数计算的适用性有待进一步研究；胡明鉴等[10]考虑细颗粒含量对钙质砂地层渗透特性的影响，发现细颗粒存在最佳含量，最佳含量细颗粒下渗透系数的变化最为显著。鞠远江等[11]通过试验研究发现细颗粒易在渗流时流失导致土体渗透性能产生变化，细颗粒流失越大渗透系数变化越大。

2 试验材料及试验过程

2.1 试验材料的物理特性

试验中采用的土样材料由黏性土-高岭土和钙质砂组成。其中高岭土是一种黏土矿物，由长石、普通辉石等铝硅酸盐类矿物在风化过程中形成，本试验中采用的高岭土目数为1 250目。钙质砂取自我国南海某地，钙质砂原材料内空隙较多，其内部特征如图1，图中圆圈表示的是内部空隙，试验中使用的材料是钙质砂原料经压碎再过筛后得到。将不同黏粒含量的钙质砂经过粒径分析激光仪测试得到其颗粒累计级配曲线如图2所示，图中s表示黏粒含量。由颗粒累计级配曲线可以得到不同黏粒含量下土样的有效粒径d10、平均粒径d30和限制粒径d60，进而根据公式(1)、(2)计算得出不均匀系数Cu和曲率系数Cc，Cu和Cc的计算公式如下：

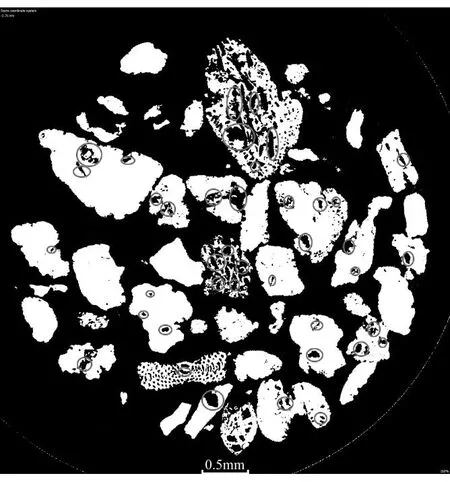
图1 钙质砂颗粒微观图(红色圆圈处为内空隙)

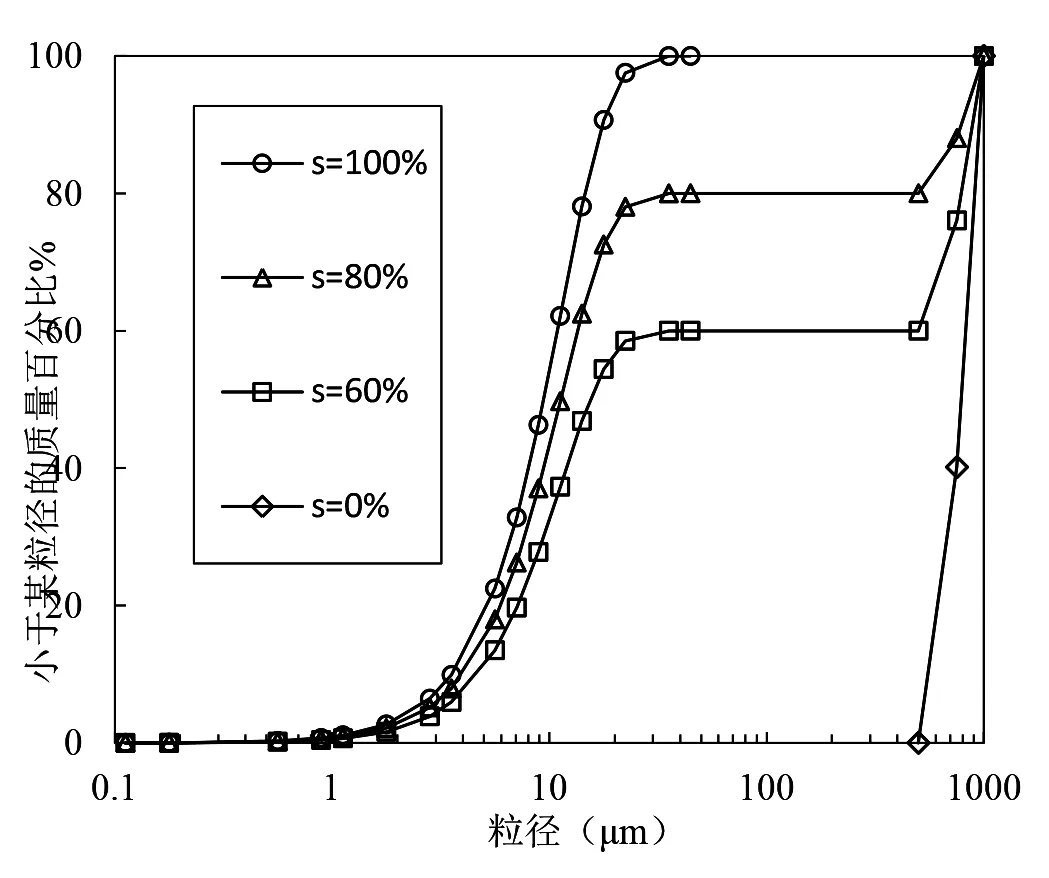
图2 不同黏粒含量的颗粒累计曲线图

(1)

(2)

不同黏粒含量下所得结果如表1所示。

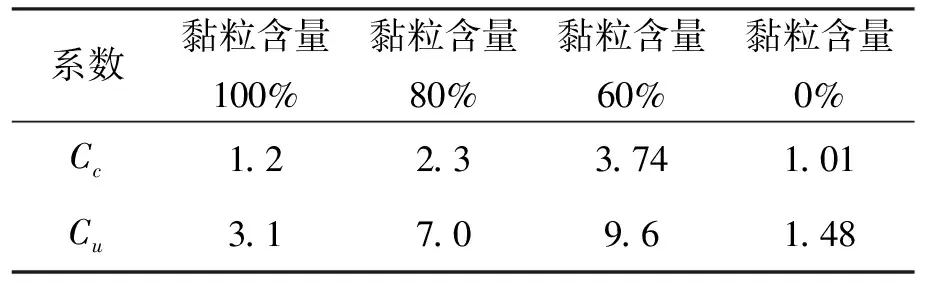
表1 不同黏粒含量下曲率系数与不均匀系数

2.2 试验过程

此试验中，钙质砂属于无黏性土，具有良好渗透性能，故此试验采用常水头的试验方法。试验中所使用的装置有渗透容器、变水头管、供水瓶、进水管等，其中常水头渗透仪主要由上盖、底座、套座、环刀、透水石和螺杆等组成。环刀内径为61.8 mm，高为40 mm，透水石的渗透系数应大于10-3cm/s。参照《土工试验规程》中的具体流程进行相应的试验步骤操作，制样前需在环刀内表面均匀涂抹适量凡士林，此步骤是防止环刀内壁渗水进而影响试验结果的准确性；为确保试样的整体性试土样填充满环刀和减少制样过程中土颗粒因扬尘造成损失，应按照孔隙比的差异选择适宜质量水分制取试样，再依据不同黏粒含量分别进行制样，每个试样分层装入圆桶，每层2 cm-3 cm厚,按质量等分5份，逐层击实，以确保试样内部空隙均匀分布。试样制取完成后，将试样放置于加满水的真空缸内抽真空，使试样完全饱和以提高试验结果的准确性，抽真空时间持续约1 h；试样饱和后，将环刀放置于渗透容器中，连接供水管和调节管，并由调节管中进水，微开止水夹，当水面与试样顶面齐平，关止水夹。降低调节管口，使其位于试样上部1/3高度处，造成水位差使水渗入试样，经调节管流出，在渗透过程中应调节供水管夹，使供水管流量略多余溢出水量，溢水孔应始终有余水流出以保持常水位；测压管水位稳定后，记录测压管水位，计算各测压管间的水位差，待渗透仪软管中有水流出开始记录数据，同时开动秒表，用量筒接取一定时间内渗透水量，重复上述步骤两次。按照公式(3)计算渗透系数：

(3)

其中，Q表示时间t内的渗透水量，L为两测压孔的试样高度，A为试样截面积，t为测读水头的时间，H为平均水位差。

为提高准确性，试样渗透系数取三次重复试验结果的平均数。

3 试验结果分析

3.1 孔隙比对渗透系数的影响

在直角坐标系中绘制不同黏粒含量下渗透系数与孔隙比的相关性散点图，反映随着孔隙比的增加渗透系数的变化规律。对不同黏粒含量下的试验结果进行线性拟合分析，并借助趋势线研究孔隙比e与渗透系数k的相关关系。对试验数据进行线性拟合，得到的拟合结果如图3所示，其中R2表示土样渗透系数k与e2(e为孔隙比)的线性相关程度。由图中可知在黏粒含量为60%时，渗透系数随着孔隙比二次方的增大也相应增大，渗透系数k与e2呈现较强的正相关关系，两者的拟合公式可以表示为：

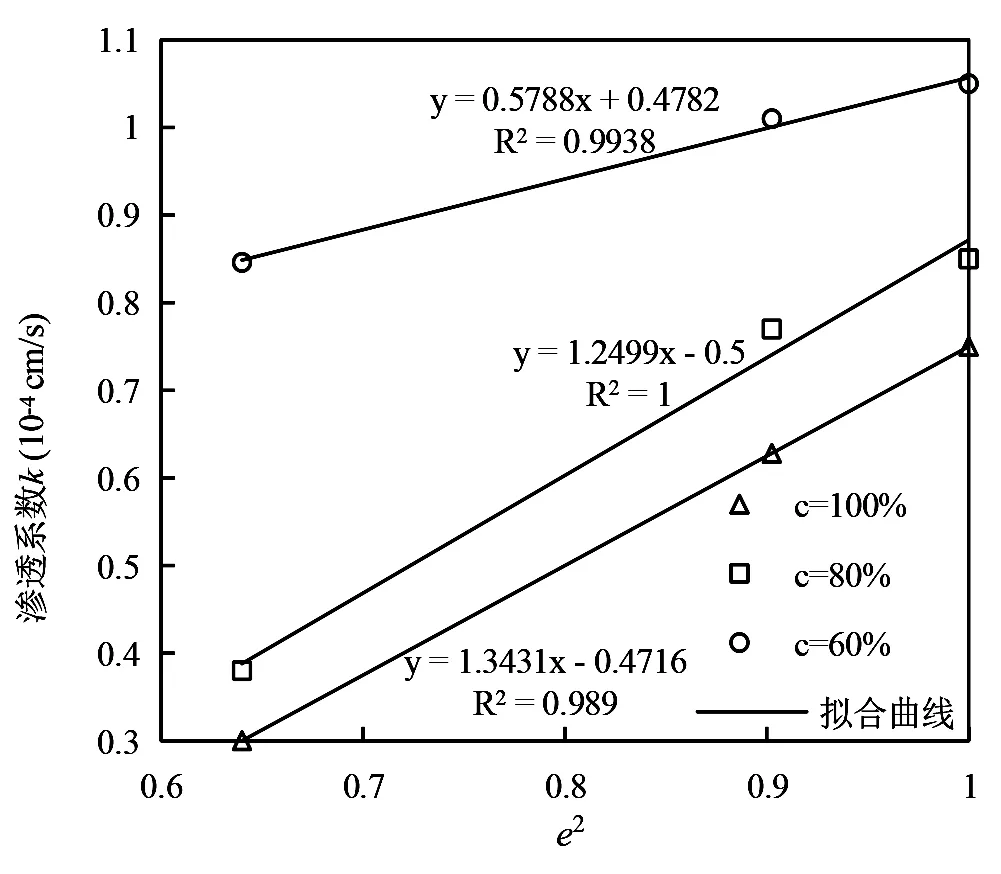
图3 渗透系数与孔隙比相关关系图

k=(0.578 8e2+ 0.478 2)×10-4

(4)

其中，相关系数R2=0.993 8。黏粒含量为80%和100%时也具有相似的规律。

从微观视角分析，在黏粒含量一定时，颗粒级配对渗透系数的影响可忽略不计，因此在孔隙比增大时，单位体积的土样内孔隙所占比率也随之增大，孔隙的平均直径也相应增大，土样内部的渗流通道也对应变宽，在压力水头一定时，水流受到的阻力变小，单位时间内的渗流量增加，由公式(3)可知渗透系数会相应变大。

3.2 黏粒含量对渗透系数的影响

将相同孔隙比下不同黏粒含量的土样击实后进行渗透试验，将不同黏粒含量对应的渗透系数绘制于直角坐标系中，如图4所示。由图可知，同一孔隙比下黏粒含量不同对应的渗透系数差异明显，渗透系数随着黏粒含量的增加而显著减小，60%黏粒含量对应的渗透系数约为纯黏粒试样渗透系数的1.5倍。从图中可以看出渗透系数k与黏粒含量s具有较高的线性负相关性，孔隙比为0.8、0.95和1时对应的相关性系数依次为0.8 572、0.9 785和0.9 643，由此可知黏粒含量对渗透系数的影响较大。在土样孔隙比一定时，内孔隙体积相同，而高岭土相比于钙质砂其颗粒较细，颗粒表面光滑、透水性差，因此在黏粒含量逐渐增大时，土颗粒之间接触更加紧密，大颗粒钙质砂之间的孔隙被细颗粒黏粒填充，内孔隙的平均直径减小，土样内部难以形成渗流通道；而在孔隙体积不变的情况下，孔隙平均直径减小，孔隙数量减少，水流渗流的路径受阻，水流通过土样的速度变缓。

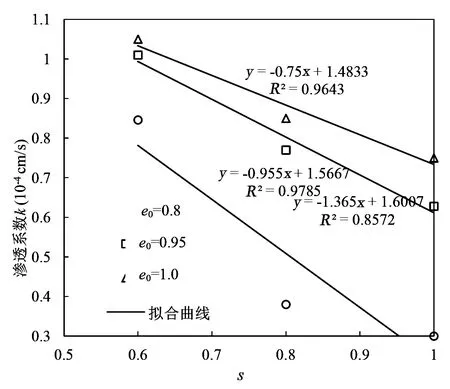
图4 渗透系数与黏粒含量相关关系图

3.3 不均匀系数和曲率系数对渗透系数的影响

将相同孔隙比下不均匀系数Cu和曲率系数Cc的乘积与渗透系数的关系表示于直角坐标系中，结果如图5所示。由图可知，随着两者乘积的不断增加，土样的渗透系数也随之增大，并且Cu·Cc与渗透系数k之间存在较好的线性相关性，孔隙比为0.8、0.95和1时，两者的线性相关系数分别为0.9347、0.9997和0.9963。不均匀系数是反映土体颗粒均匀程度的一个指标，不均匀系数越大表示土体中颗粒粒径的涵盖范围越大；曲率系数是反映土体颗粒粒径连续性的一个指标，曲率系数大于1小于3表示土粒的粒径齐全，连续分布。

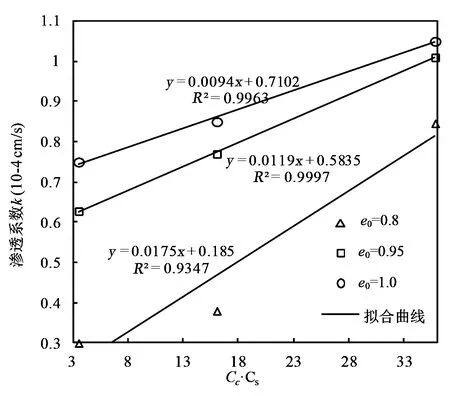
图5 渗透系数与不均匀系数和曲率系数相关关系图

在不均匀系数与曲率系数乘积Cu·Cc较大的情况下，颗粒粒径的大小差异较大，且存在某些粒径的颗粒缺失，而较粗颗粒之间的孔隙需要细颗粒填充，而在孔隙比一定时，Cu·Cc越大粗颗粒之间的孔隙被细颗粒填充比率较小，因而更容易形成渗流通道致使渗透系数变大。

3.4 颗粒大小对渗透系数的影响

由图1可知不同黏粒含量下有效粒径d10变化规律较为明显，并且根据以上研究结论发现粗颗粒越多，颗粒间空隙越大，渗透系数越大；反之细颗粒越多，颗粒间空隙越小，渗透系数越小。因此研究颗粒大小对渗透系数的影响具有一定的研究意义，本文主要研究细颗粒对渗透性的影响，而在颗粒累计级配曲线中d10可以较好反映细颗粒的占比，故本文针对d102与渗透系数k的关系进行研究。在保持土样孔隙比不变的条件下，将d102与渗透系数的关系绘制于直角坐标系中，如图6所示。由图可知，随着d102的逐渐增大，土样的渗透系数也随之增大，且两者之间的相关性程度较高。当黏粒含量为0.8、0.95和1.0时，d102与渗透系数的线性相关度依次为0.953 3、0.999 5和0.999 6。从微观角度分析，当d102较小时，细颗粒未能完全填充粗颗粒间空隙，使得细颗粒受到的包裹和约束力较小，在水流通过时细颗粒被带走，进而形成渗流通道，因此对应的渗透系数相比d102时较小。

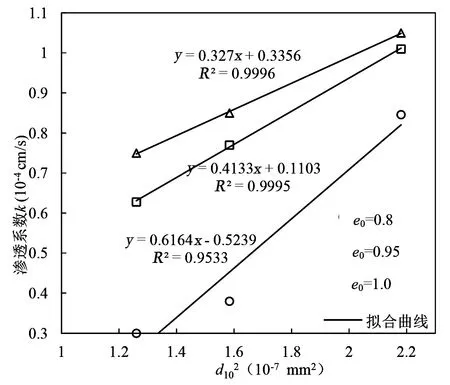
图6 渗透系数与颗粒大小相关关系图

4 渗透系数计算公式

对各种影响因素单独分析，并进行数据整合和线性拟合可以发现土样的渗透系数与e2(e为孔隙比)、黏粒含量s、不均匀系数Cu和曲率系数Cc的乘积Cu·Cc有较高的相关性。本文采用因素分析法研究每个因素对渗透系数的影响作用，该方法通过改变某一因素而保持其他条件不变,通过分析渗透系数与单一因素的相关关系得出相应的拟合公式，发现每个影响因素与渗透系数都呈现较好的相关性。为了能体现各个影响因素的综合作用，可以把各参数相乘并对得到的公式进行修正，建立通用的经验公式以表征土样渗透系数的计算过程，拟将公式应用于实际工程中为计算渗透系数提供参考，所得公式如下：

式中，k为渗透系数(cm/s)，B为无量纲。将试验所得数据代入建立的经验公式，反复验算以推算出无量纲B的值。通过反演计算，可以得出当B取0.024时渗透系数计算值与试验所得实际值之间差异较小，因此取B=0.024。

为了验证本文得出的经验公式的可靠性，将本文经验公式计算值k、太沙基公式计算值kT、哈增公式计算值kH、苏立君公式计算值k苏、朱崇辉公式计算值k朱与渗透系数实测值的比值列于表2中。

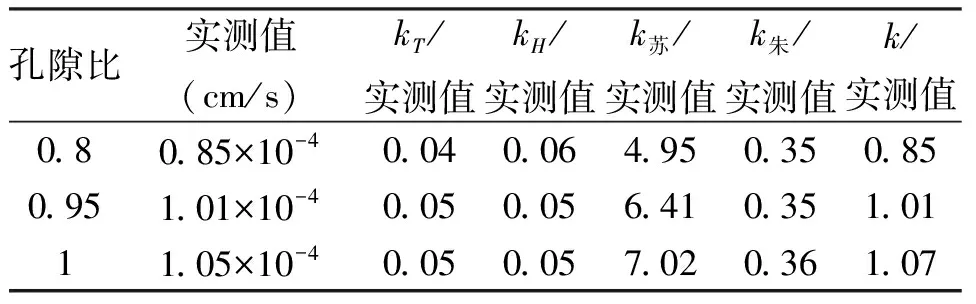
表2 渗透系数经验公式计算值与实测值的对比表

经过对比分析发现，本文提出的经验公式计算结果相比于上述公式计算结果精确度有较大提高。经验公式计算值与实测值的比值在0.80～1.10之间，表明此经验公式准确性较好，可以为实际工程提供参考，特别是对于含有黏粒的钙质砂工程，一定程度上解决了计算其渗透系数的难题，实用性较高。由表可知各种渗透公式计算所得结果差异明显，造成此现象的原因可能在于各种方法研究的对象和工况不同，其他研究者大多研究单一土类的渗透系数影响因素，但实际情况下土体成分多样，内部结构极为复杂，即使产生细微变化，对渗透系数的影响也可能极其明显，因此如何利用有效的方法和合适的颗粒组成模拟实际工程中复杂多变的工程状况是后续研究的重点。