基于MATLAB惯量电模拟异步电机的建模与仿真
2022-10-02王龙龙党金金
王龙龙,党金金
(洛阳职业技术学院 汽车与轨道交通学院,河南 洛阳 471400)
车辆底盘测功机是非常重要的试验设备,它通过道路模拟系统真实再现汽车在道路上行驶时的工况,从而能够对汽车动力性、经济性等各项指标进行准确测量。因为在底盘测功机上试验时汽车处于静止状态,所以底盘测功机必须能够对汽车在道路上试验时产生的惯量进行准确模拟。底盘测功机惯量电模拟,即用加载电机代替原有的机械飞轮组,通过控制电机的输出扭矩与机械飞轮的惯性扭矩相等,从而实现汽车惯量的模拟。惯量电模拟因能够实现惯量的无极调整,减小测试系统体积和运行噪声,提高设备的自动化程度,使操作更加方便而被广泛应用。
交流异步电机因为结构简单、工作可靠,寿命长、价格便宜等诸多优点在工业领域得到了广泛的应用。本文在建立交流异步电机数学模型的基础上,结合坐标变换,利用MATLAB仿真软件中的Simulink工具箱搭建了异步电机直接转矩控制系统的仿真模型,并对某型汽车在DCG-10E型底盘测功机上进行滑行试验时所需补偿的惯性扭矩为例进行了仿真分析。
1 电模拟电机补偿扭矩的计算
1.1 机械飞轮惯量的计算
汽车在道路上进行试验时,被试汽车的动能分为平移质量的动能和旋转部件产生的动能,可以表示为
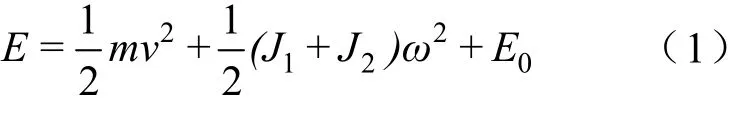
式中,为汽车质量;为驱动轮的角速度;为汽车速度;为汽车驱动轮的转动惯量;为汽车从动轮的转动惯量;为汽车传动系统零部件旋转产生的动能。
汽车以相同速度在底盘测功机试验时,试验台和汽车的动能为

式中,为飞轮转动惯量;为测功机滚筒转动惯量;为电力测功器转子的转动惯量;为飞轮的角速度;为测功机滚筒的角速度;为电力测功器的角速度。
因为飞轮与底盘测功机滚筒之间通过电磁离合器联接,所以==,=。
由式(1)和式(2)相等可得飞轮的转动惯量为

式中,为汽车驱动轮的半径;为底盘测功机滚筒的半径。
1.2 电模拟电机补偿转矩的计算
电模拟电机转子受力示意图如图1所示,由牛顿第二运动定律可得,电机转子的动力学方程为
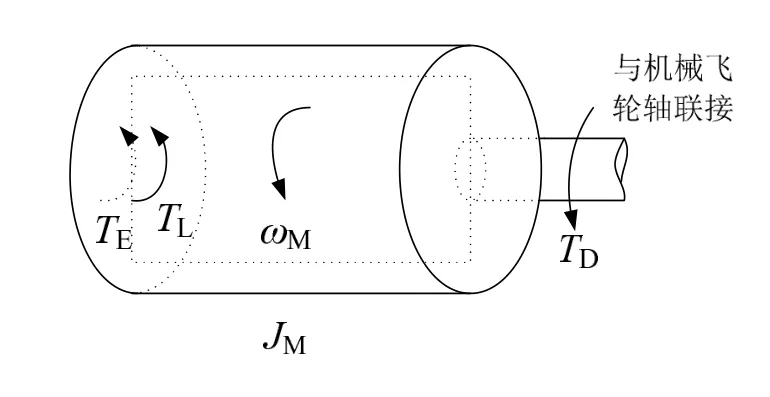
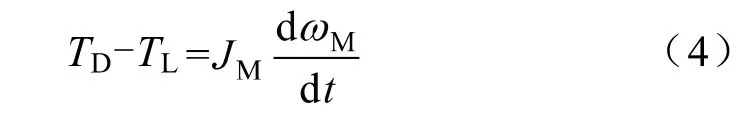
式中,为加载电机转子的转速,rad/s;为转子的转动惯量,kg.m;为电机轴所受驱动扭矩,Nm;为电机所受的电磁扭矩,Nm。
当在飞轮轴上安装转动惯量为的机械飞轮组时,那么在相同的扭矩作用下电机转子的动力学方程为
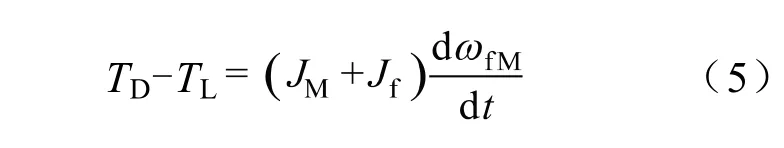
式中,为添加飞轮时电机转子的转速,rad/s。
显然与不相等,想要使两者相等,那么电机就必需补偿出机械模拟时飞轮产生的惯性扭矩,那么式(4)可以写为

式中,即为模拟转动惯量为的机械飞轮时电机需要动态补偿的扭矩。
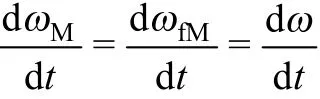

2 异步电机数学模型与直接转矩控制原理结构图
2.1 异步电机的数学模型
异步电机由其自身构造决定了其具有阶数高、强耦合、非线性等特点,为了便于异步电机数学模型的建立,特做如下假设:
(1)异步电机的三相绕组呈对称分布。
(2)忽略异步电机定子和转子之间的齿槽效应。
(3)异步电机的铁损和磁滞损耗都忽略不计。
(4)忽略温度变化对异步电机绕组的作用。
则异步电机在坐标系中的电压方程为
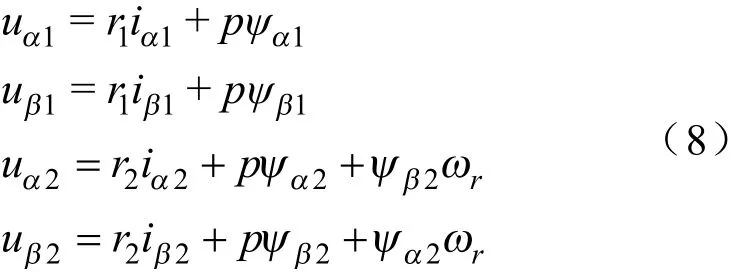
式中,u、u为异步电机定子坐标系中的电压分量;i、i为异步电机定子坐标系中的电流分量;u、u为异步电机转子坐标系中的电压分量;i、i为异步电机转子坐标系中的电流分量;、分别为异步电机的定子和转子的电阻;为微分算子;ψ、ψ分别为异步电机定子在坐标系下的磁链分量;ψ、ψ分别为异步电机转子在坐标系下的磁链分量;为异步电机转子的角速度。
异步电机在坐标系中的磁链方程为
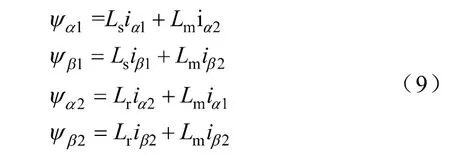
式中,为异步电机定子的自感;为异步电机转子的自感;为异步电机定子和转子之间的互感。
异步电机在坐标系中的电磁转矩及转矩方程为
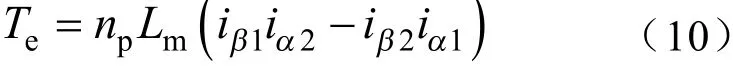
式中,为异步电机的极对数;为异步电机的转矩。
电机的运动方程为

式中,为电机负载转矩;为异步电机的转动惯量。
2.2 异步电机直接转矩控制系统结构图
根据异步电机直接转矩控制基本原理,直接转矩控制系统主要是要解决异步电机磁链幅值的控制和异步电机电磁转矩的控制这两个问题。这两个问题可以用电压空间矢量的选择切换来解决。异步电机直接转矩控制系统主要由三相/两相变化单元、电机转矩观测单元、电机磁链观测单元、坐标变换单元等单元组成。
3 异步电机直接转矩控制模型的建立
3.1 异步电机仿真模型
异步电机在两相静止坐标坐标系下的数学模型包括多个微分方程,使用Simulink建模就是对微分方程的求解。利用MATLAB中的Simulink工具箱对动态系统进行建模和仿真。本文使用Simulink工具箱中的S-Function函数构造了异步电机的仿真模型,如图2所示。

3.2 转速和转矩调节
转速调节主要是通过比例积分微分(Proportion Integration Differentiation, PID)调节器,以给定转速和电机反馈转速的差为输入量,通过调节PID调节器的参数,控制电机输出转矩为定值。转矩调节主要通过滞环比较器来调节,输入为给定转矩和观测转矩的差,输出为开关信号。
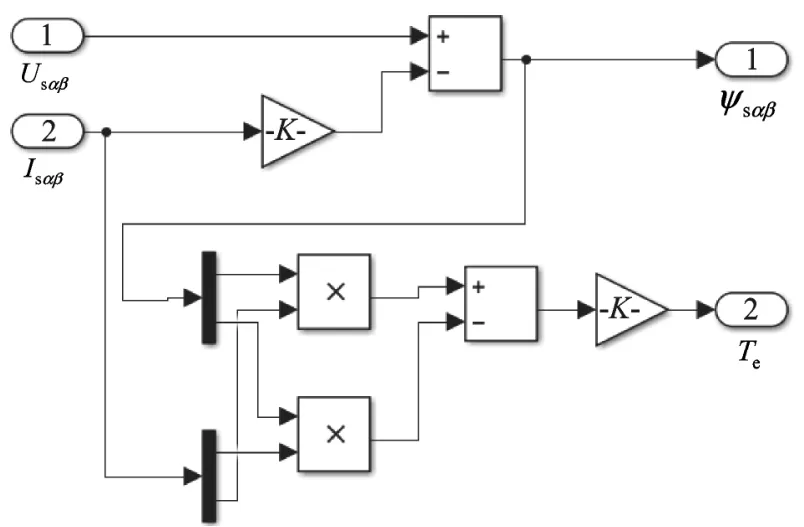
3.3 异步电机定子磁链观测模型
磁链观测模型如图3所示,磁链测量的准确与否对异步电机直接控制有着重要的影响,直接决定逆变器开关状态的选择。因为异步电机定子磁链很难进行直接测量,所以本文通过间接测量的方法获得异步电机定子磁链的值,即通过测量异步电机的转速和定子电压,再根据式(12)求出。
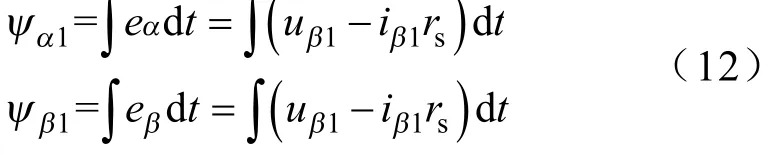
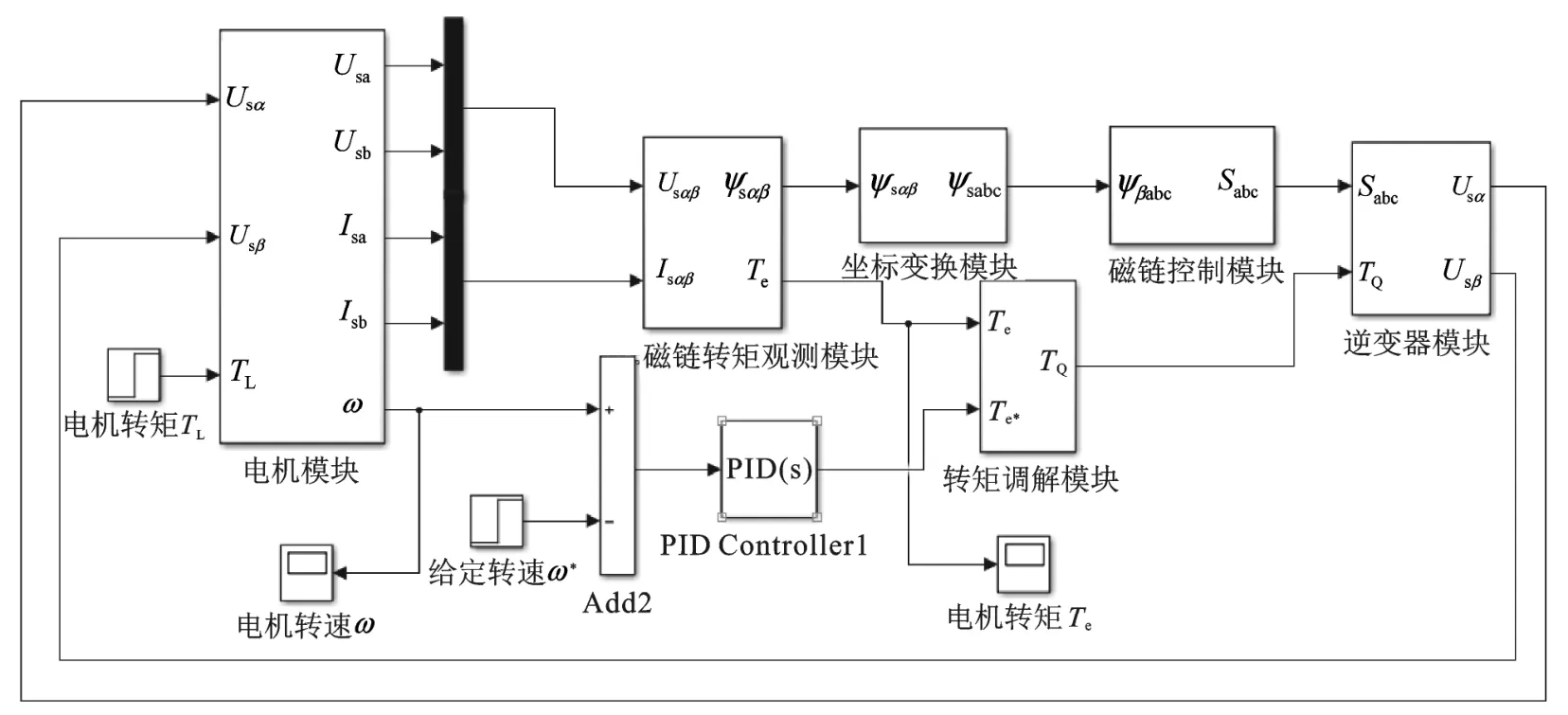
3.4 异步电机直接转矩控制系统的仿真模型
异步电机直接转矩控制系统的Simulink仿真模型如图4所示,模型主要由电机模块、磁链转矩观测模块、坐标变换模块、磁链控制模块、转速和转矩控制模块、逆变器模块构成,逆变器模块用M-funciton函数实现,这里不再详细说明。
4 惯量电模拟电机加载转矩仿真分析
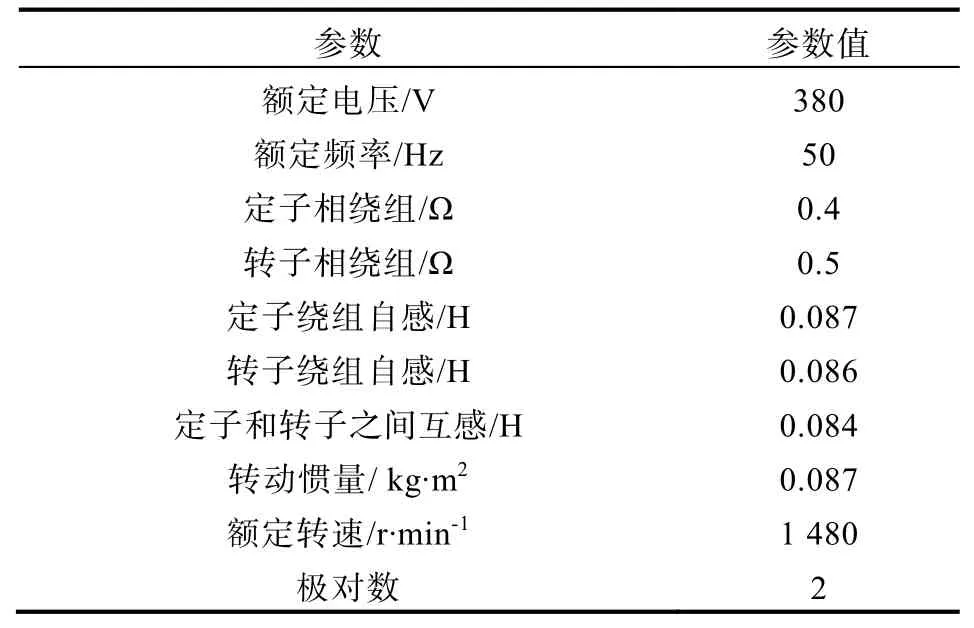
为了保证车辆在底盘测功机上试验时的准确性,对惯量电模拟时所用电机进行了仿真分析。由式(7)计算某型号车在DCG-10E型底盘测功机上试验时需要补偿的扭矩,选取Y225S-4型异步电机为加载电机,并以Y225S-4型号电机为例进行仿真分析,电机参数如表1所示。
为了验证本文设计异步电机直接转矩控制系统仿真模型的稳定性、准确性和静态与动态性能,仿真时先空载启动,当系统进入稳定状态后,在=0.25 s时突然施加=30 Nm的负载转矩,仿真得到异步电机的转速和转矩波形图如图5所示。
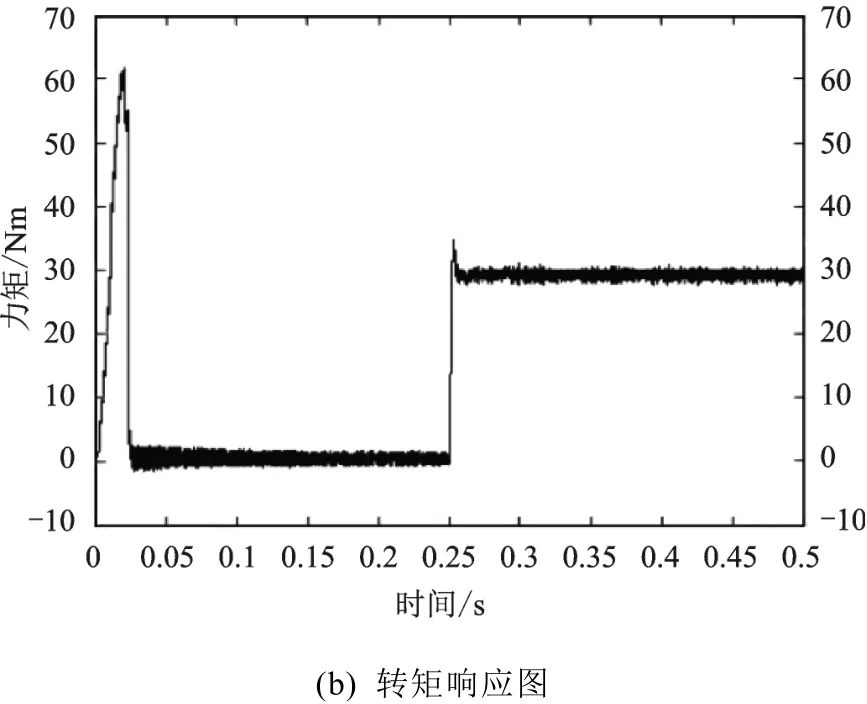

由仿真结果知,在空载启动下,在=0.05 s时,电机转速达到额定转速,同时电机电磁转矩稳定在零附近。说明该系统响应速度快,并且准确;在=0.25 s时突然施加=30 Nm的负载转矩,电机转速突然下降,但是又在很短时间内恢复到平衡状态,转矩也在很短时间内由零变为30 Nm,并稳定。仿真波形图说明本文所搭建的异步电机直接转矩控制系统仿真模型的准确性和合理性。
5 结论
本文基于汽车驱动轮动态特性相同的原理,推导出惯量电模拟是加载电机的补偿转矩。为了更好地实现惯量电模拟,在分析异步电机数学模型的基础上,利用MATLAB中Simulink工具箱搭建了异步电机的直接转矩控制系统仿真模型,并对电模拟所需电机进行仿真分析,仿真波形图说明搭建的仿真模型能够快速、准确地对异步电机进行控制,为交流异步电机在底盘测功机惯量电模拟中的应用提供了参考。
