基于块稀疏编码的物联网无源定位机器学习
2022-10-01李晓茹
江 河,李晓茹,孙 敏
(1.太原学院 计算机科学与技术系,山西 太原 030012;2.山西大学 计算机与信息技术学院,山西 太原 030006)
0 引 言
作为无线定位技术的一种,无源定位(device-free localization,DFL)技术[1]作为在物联网环境下提供高质量服务的新兴技术,得到了广泛的关注[2,3]。由于DFL可以在不携带任何附加设备或标签的情况下定位目标,所以催生了大量新兴的工业和家庭应用,如安全防护中的入侵检测、移动机器人定位,以及患者和老年人的医疗监控等[4,5]。
传统的无源定位中由于传感器节点生成的数据具有与特定目标位置相关且与其它节点不同的特定模式,因此模式信息可用于定位。从这个角度出发,以往的研究将定位问题转化为分类问题[6]。为了解决分类问题,许多流行的机器学习方法如k-最近邻(KNN)[7]、支持向量机(support vector machine,SVM)[8]和深度学习[9],可用于精确的单目标定位。然而,对于多目标定位问题,现有的分类方法如深度自动编码器和KNN等,需要配置复杂的决策规则,且定位精度较低。为了精确定位目标,先前的研究已经提出了许多方案。文献[10]利用贪婪匹配追踪(greedy-matching pursuit,GMP)算法解决了l1范数正则化最小化问题。文献[11]利用CS建模目标函数中的1范数,采用贝叶斯贪婪匹配追踪(Bayesian greedy-matching pursuit,BGMP)方法进行单目标定位。文献[12]将DFL描述为一个稀疏表达分类问题,并通过稀疏编码来定位单个目标来解决最小化问题。然而,上述方法中DFL数据中自然群稀疏性的研究并不充分。此外,由于稀疏解的元素索引与网格ID相关,0范数或1范数方法通常通过选择稀疏解中的最大值来估计目标位置。然而,在实际场景中,目标可能具有不同的大小或尺寸类型。解决这一问题的有效方法是在原始信号中引入相位偏移或振幅变化,从而使攻击者或入侵者无法获得正确的感应信号,这种方法在很大程度上导致了信号衰落,严重降低了解码信噪比,因此,有必要开发一种鲁棒可靠的DFL算法,使其能够在这种具有挑战性的情况下工作,并具有良好的信号恢复性能。
针对上述问题,提出了一种基于块稀疏编码的物联网无源定位机器学习算法,并通过实验验证了提出算法能够有效克服无源定位相关的机器学习算法不考虑群体结构,定位精度低,可靠性差等缺点。
1 建立模型
1.1 准备工作
如图1中的步骤(1)所示,为了更方便进行DFL操作,检测区域被几个无线发送器-接收器节点包围,并且将其分割成多个网格。没有将无线节点有规律地进行分布,其位置也不一定是已知的。由于存在散射、衍射和吸收,目标会影响信号的广播,从而改变每个节点的统计平方公差(received signal strength,RSS)的测量值。当目标位于网格上时,可以检测到包含特定RSS测量的联合信号配置。此外,从封闭的目标位置感应到的RSS信号通常表示出类似的特征。因此,如果将目标捕获的网格视为一种类别,则目标定位问题可以转化为分类问题。
另外,如果将RSS测量值视为图像的像素值,可以将收集的RSS信号构建为具有特定模式的RSS图像。此外,由于RSS测量的信号基础比目标引起的信号变化要强得多,因此重要的特性通常会被淹没在原始信号中。这将不利于定位分析。为了克服这一问题,采用背景消除策略对原始信号进行预处理。然后得到具有明显特征的RSS变异图像,当目标在不同的检测区域网格内移动时,将得到不同的RSS信号变化特征。
1.2 DFL信号的稀疏表示模型
1.2.1 数据采集及背景消除
根据式(1)消除背景
(1)
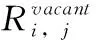
假设无线传感器节点总数为N。 如图1中步骤(1)的说明,每个节点作为时间日程表发送无线信号,而其它节点接收和测量信号。然后,得到由N个所有节点的变化组成的矩阵ΔR,如式(2)所示
(2)
式中:c是目标捕获的网格的索引,l是目标位于第c个网格时的样本索引。 ΔRi,j中的i是输入ID,j是接收ID。
1.2.2 构造数据集
构造数据集主要分为以下两个步骤:
(1)构建传感矩阵。如图1中步骤(2)所示,假设检测区域中有C个网格,每个网格被视为一个类别。在这个区域中,所有潜在目标的位置都被归为C个类。对于每一个类c=1,2,…,C, 当一个物体在相应的网格上时,令l=1,2,…,L, 共进行了L次实验。
(2)在线状态处理测试信号。在此状态下采用了类似的处理过程,包括数据收集、背景消除和矩阵到向量的转换。当目标T定位在不同的网格上时,得到观测信号y,其中T必须小于总网格数。如果T=1时,是单目标定位,则当T>1时,为多目标定位。
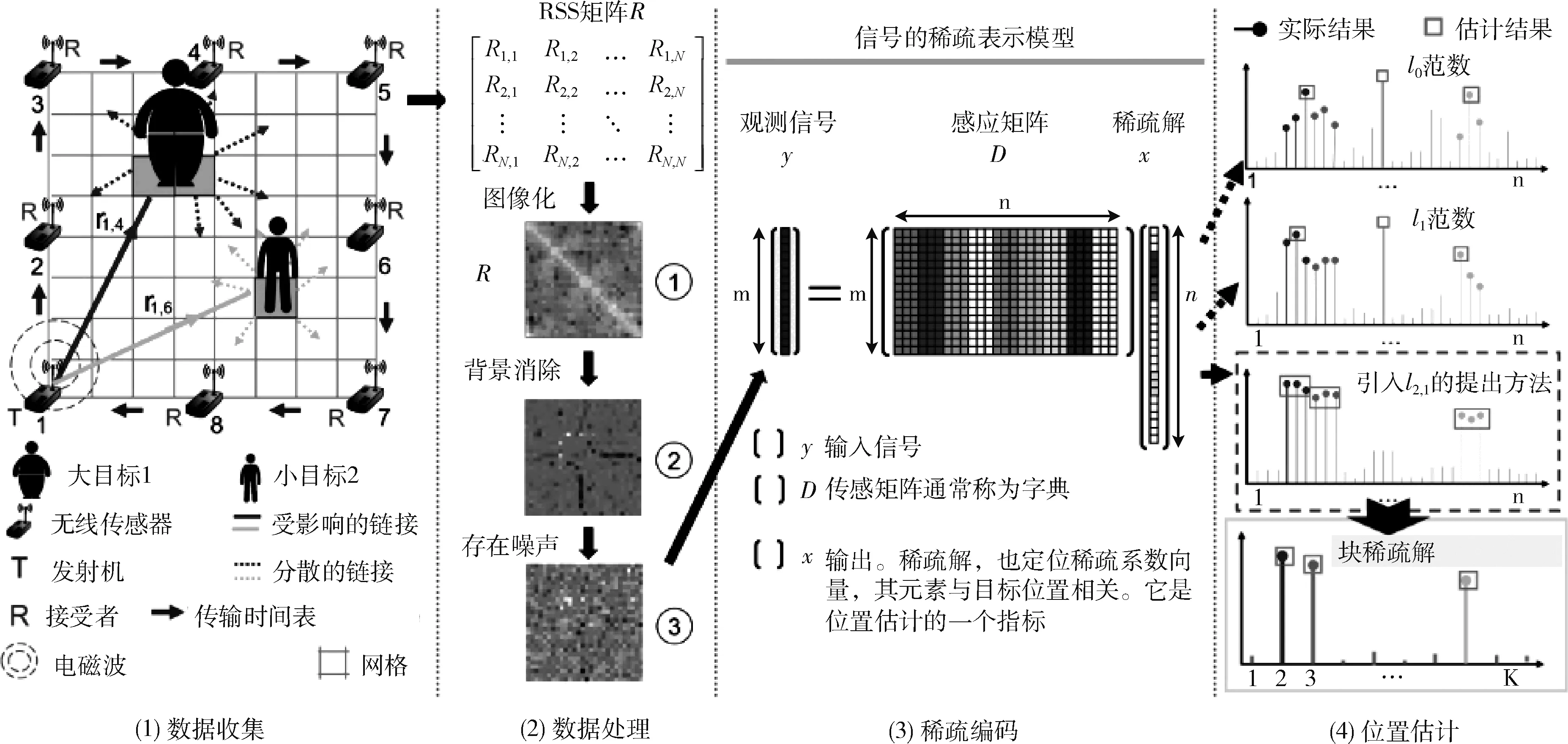
图1 块稀疏编码结构框架
1.2.3 测试信号的稀疏表示
现在将定位问题进一步表述为稀疏表示分类问题,其实质就是将定位问题转换为寻找识别匹配问题。为了便于理解稀疏表示模型的原理,首先看一下图2(a)中的一个简单示例,其中将检测区域分割为9个网格,即C=9, 因此,矩阵包括9类样本。由于同一类数据之间存在高度一致性,因此每个类的数据空间分布表现如图2(b)所示。这就导致了测试信号优先选择同一类中的基础样本来表示自身的现象。因此,如图2(a)所示,当测试信号属于第一类时,用三角形标记的样本代表测试信号。方块表示测试信号,其它符号是矩阵的样本。
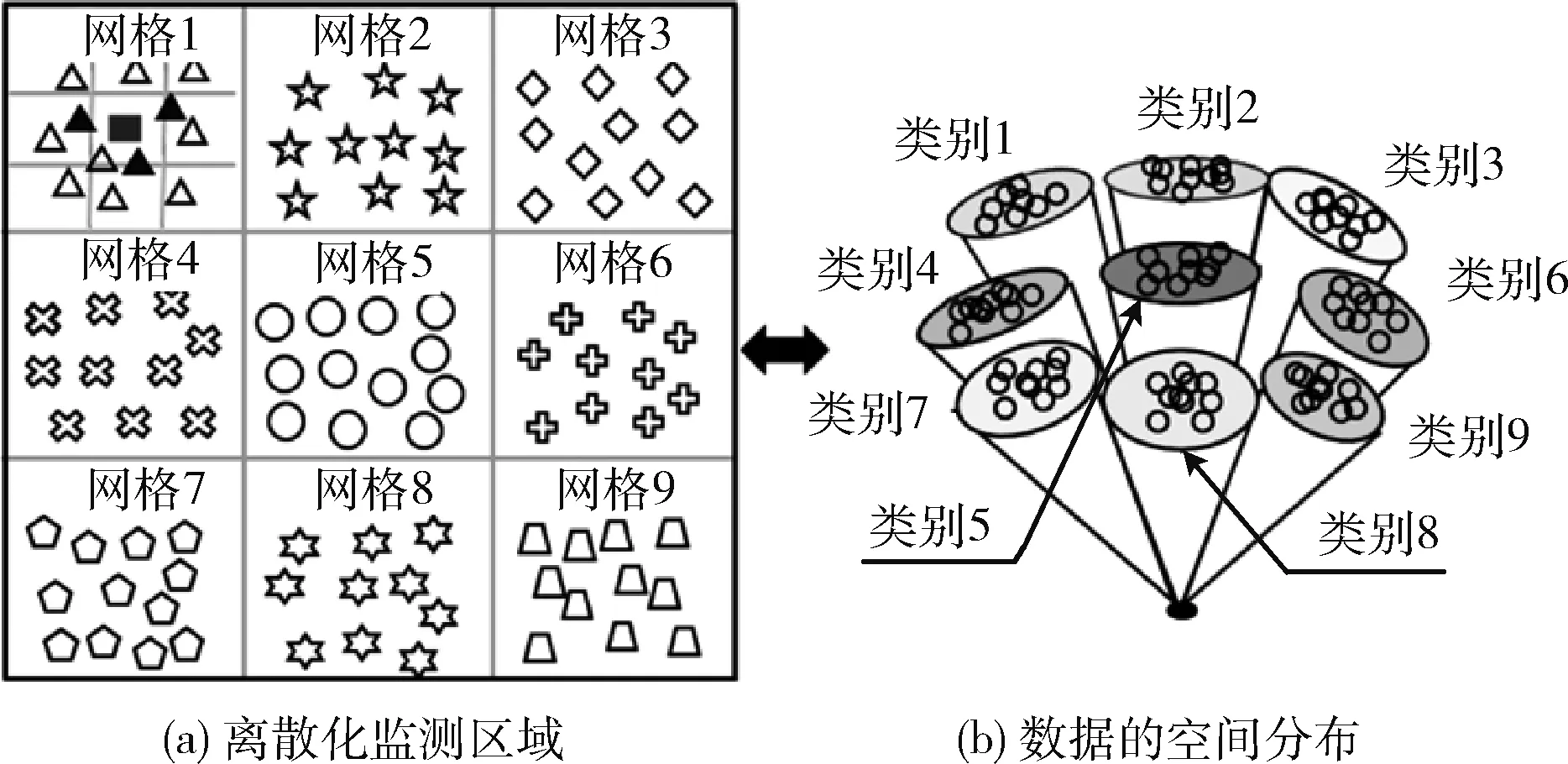
图2 测试信号稀疏表示分类
从上文分析可知在线状态时,当目标位于检测区域时,得到测试信号y。此处以两个目标为例,假设目标分别位于第p个网格和第q个网格。如果给定足够的样本,测试信号y可以用矩阵D的两个相应样本集线性表示,该线性表示如以下公式所示
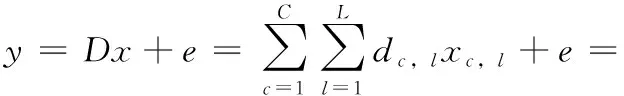
(3)
式中:x=[0…0xp,1…xp,L0…0xq,1…xq,L0…0]T∈Rn是一个由系数组成的向量;xp,j和xq,j∈R(1 总之,观测信号y可以用矩阵D中n个基础样本稀疏表示。从这个角度来看,式(3)变成了稀疏表示问题,其中x是稀疏系数向量,其非零元素与目标位置相关。基于式(3),一旦稀疏解即稀疏系数向量x被确定,目标的准确位置就被估计出来了。因此,DFL问题本质上是一个稀疏表示分类问题,可以很好地用稀疏表示模型来表示。 2.1.1 稀疏编码存在的问题 稀疏编码是基于矩阵D和观测信号y寻找一个包含小部分非零值分量的潜在向量变量,称为稀疏。在实际应用中,为了获得精确的DFL,在构造矩阵时需要大量的样本。这导致基础样本总数n大于字典数m的可能性很高。因此,式(4)通常是一个不确定系统,其解不是唯一的,即问题是不固定的。 然而,通过选择最稀疏解,可以使问题确定下来。这启发了本文用稀疏正则化方法来解决最优化问题,以找到最稀疏解。最常用的稀疏正则化项是l0范数和l1范数,但是用l0来寻找待定系统中线性方程的最稀疏解是NP难问题。l1范数将稀疏模式独立地看作一个单粒子,在个体水平上产生稀疏性。相比之下,由于目标位置较近,导致了DFL数据的内群结构,个体选择l1范数和l0范数会降低定位精度。 2.1.2 具有块稀疏模式的新目标函数 为了确定最稀疏解,本文利用l2,1范数作为正则项来进行分组,在稀疏解中生成块稀疏模式。目标函数如式(4)所示 (4) 2.2.1 基于近端算子的块稀疏编码 虽然等式(4)不是光滑的,但它有全局最优解。通常采用次梯度法求解式(4),通过对式(4)求导,并令其为零,可以得到最小值x* (5) (6) 为了与式(6)一致,本文基于式(4)进行了修改。修改和推导的过程在附录部分有详细的说明。那么,接下来考虑比式(4)更简单的目标函数的最小化方法,如式(7)所示 (7) 式中:K被视为已知常数,因为它和x没有关系;μ是一个比例因子,其值应大于 (DTD) 的最大特征值e, 例如1.01×e;b是与x大小相同的中间变量,推导过程如以下公式所示 (8) (9) (10) 2.2.2 基于块稀疏解的目标定位 为了便于位置估计,将x*转换成块稀疏解β* (11) (12) 提出的定位算法简称BSCPO,其伪码如算法1所示。原始目标函数(13)的方程如下 (13) 通过对式(13)求导,并将其等于零,可以得到最小的x*如式(14)所示 (14) 修改后的目标函数如式(15)所示 (15) 式中:K是已知常数,与x无关。μ是大于 (DTD) 最大特征值的比例参数,例如,设为最大特征值的1.01倍。b是中间变量,和x的大小一致。以上就是从式(13)~式(15)的修改和推导的详细过程。式(13)中的J(x) 不易取得最小值,因为求解 (DTD)-1的计算量非常大,而且容易出错。因此构造了一个新的函数,避免用最大最小化(MM)优化算法求解 (DTD)-1。 根据MM的原理,找到一个Hk(x), 以便在每次迭代中,可以选择在x(k)处与J(x) 一致的Hk(x) 值,否则上界J(x)需要满足以下条件: (1)Hk(x)≥J(x), 对于全部x (2)Hm(x(k))=J(x(k)) 利用体视显微镜或金相显微镜观察分析剪切破坏后的焊接连接面的表面状态,以评估焊接质量,分析强度值形成原因。 然后,用以下公式进行推导 Hk(x)=J(x)+x的非负函数 (16) (17) 其中,μ必须选择等于或大于 (DTD) 的最大特征值。那么 (μI-DTD) 是一个半正定矩阵,这将推导出 vT(μI-DTD)v≥0, ∀v μ≥(DTD)的最大奇异值 (18) 由此得到了期望的Hk(x) 值。下面检验新函数对x的导数 (19) (20) 将式(20)和式(14)相比,可以看出式(20)无需求解 (DTD)-1, 这将大大节省计算量。最后,通过式(21),可以得到修正后的目标函数 (21) 令 (22) 就可以得到下面的二次表达式 (23) 式中:K1由式(22)的前两项组成,和x无关。K和x有关,是关于x的常数,关系式如下 (24) 因此,式(15)中的问题P(x) 等于最小化式(23)中的Hk(x)。 算法1:基于邻近算子的块稀疏编码 输入:y∈Rm,D∈Rm×n,μ,λ,x0=0 输出:φ1,…,φs (1) for k=0 to 最大迭代次数 do (4) 直到满足收敛准则或达到最大迭代次数。 (5) end for (6)x*←x(k+1) (7) 根据式 (12)β*←x* (8) 根据式 (13) 估计目标位置位于第φ1、φ2、φS个网格 (9) 返回{φ1,…,φS} 在室外无源定位的真实实验数据集上验证本文提出的方法的性能。实验环境是Matlab R2016b,硬件配置为64位、8 GB内存和Intel CoreTM i7 CPU系统为Windows10的计算机。 如图3所示,方形检测区域面积为21×21英尺,被分割成36个网格,周围有28个TelosB传感器节点。每个传感器节点的工作频段为2.4 GHz。两个相邻节点之间的间隔距离为3英尺,每个节点距地面3英尺。基站监听整个网络流量,通过USB端口将采集到的实时数据传送到计算机。在每个网格上,进行30次实验,每次时间间隔都较短。每个网格分配有一个网格号,最左下角的网格为1号网格,从左往右,从下往上依次编码。 图3 DFL系统的实验装置 对于单目标定位实验,将RSS样本矩阵分为两部分,其中25个样本用于构建字典,其余样本为测试样本;对于多目标定位实验,它与单目标实验共享同一个字典,而测试信号来自两个定位目标的新RSS示例。矩阵大小为784×900,每个测试样本大小为784×1。 3.1.1 背景消除时采用的数据预处理 由于原始RSS信号是直接从环境中测量的,可能包含很多无用的信号分量,这些分量比有用的信号波动更强烈。例如,即使在检测区域中有目标,背景信号也不会改变。因此,有必要对背景像素进行预处理。在室外DFL实验中,通过从Rtarget中减去Rv acant进行数据预处理,如图4所示。经过预处理后,可以消除大部分无用信号分量,且信号变化明显。 图4 数据预处理的示例 3.1.2 不同方法的性能比较 l0和l1范数是DFL领域中最流行的稀疏正则化范数,许多相关文献证明了它们的有效性。因此,比较了本文提出的BSCPO算法与含有l0范数和l1范数的算法的性能。此外,为了验证所提出的块稀疏算法的性能有所提高,本文还将其与多基线和最新的机器学习算法进行了比较,包括具有卷积自动编码器(CAE)的深度神经网络、一维卷积神经网络(CNN-1D)、支持向量机(SVM)、KNN、基于迭代收缩阈值算法的稀疏编码(SC-ISTA)和正交匹配追踪稀疏编码(SC-OMP)。 3.1.3 其它参数设置和指标 为了明确算法的性能评价和结果比较,本文将定位的精度作为评价算法性能的指标。为了保护隐私,在原始RSS信号中加入了严重的高斯噪声,以防止网络相关隐私泄露给入侵者或攻击者。在实际应用中,DFL系统会不可避免地受到环境噪声的干扰,例如周围无线设备引起的电磁干扰。因此,信号的恢复性、鲁棒性和可靠性对DFL算法至关重要。本文用信噪比来衡量信号质量。SNR定义为SNR(dB)=10log10(Psignal/Pnoise), 式中:Psignal和Pnoise分别代表信号功率和噪声功率。另外定位准确率(%)表示提出方法定位的准确样本与所有定位样本数的比值。 3.2.1 单目标定位方法的性能 该方法当DFL系统受到严重噪声干扰时仍具有较好的鲁棒性能。图5描述了当目标位于检测区域的第36个网格处时的示例。从图5(a)中,与图4(c)的原始无噪声信号相比,测试信号受噪声污染更严重。尽管存在这种不利条件,但由于块稀疏解的相关元素是非零的,所以通过块稀疏解,目标仍然可以精确被定位,模型已较清晰地重构测试信号,这也可以验证模型的有效性。 图5 对无噪测试信号和有噪测试信号进行成像 如图6所示,用一个例子解释了本文方案比具有l0范数和l1范数的算法能更好地处理DFL。通过l0范数或l1范数的稀疏解,由于噪声的影响,另一组的元素值大于真实值,从而导致目标位置估计错误。相比之下,使用BSCPO的群稀疏解,由于最大元素与真实情况一致,因此可以正确地定位目标。对所有测试样本进行测试,图7给出了BSCPO的定位精度以及在各种噪声条件下的结果比较。从图7可以看出,本文提出的BSCPO算法在定位精度和鲁棒性方面都优于引入l0范数和l1范数的算法。当带有噪声的测试信号和带有噪声的字典的信噪比分别超过-10 dB和-20 dB时,BSCPO定位精度达到100%。 图6 算法性能比较 图7 算法的定位精度 如图8所示,以无线发送器-接收器-传感器为例来展示本文算法的恢复性能和去噪性能。噪声信号的信噪比为-5 dB。从图8可以看出,在噪声信号和原始信号之间存在一些明显的振幅偏移。通过BSCPO算法进行去噪处理,信号几乎可以完全恢复,两个恢复的信号分别与对应的无噪声原始信号非常接近。 图8 提出的BSCPO算法的信号恢复性能 3.2.2 对比分析 将本文方案与其它6种机器学习方法进行比较,除了先前讨论过的具有l0范数和l1范数的算法。特别是,Deep CAE[13]、SC-ISTA[14]和SC-OMP[15]是当前最先进的DFL算法,均采用了本文的数据集。SC-ISTA、SC-OMP和KNN使用未经消除背景的原始RSS信号。因此,在不同实验中设置相同的条件。此外,还使用了常用的基本分类方法进行了实验,有支持向量机和一维卷积神经网络(CNN-1D)。对于支持向量机,采用一对一策略和径向基函数核进行多分类。 比较结果见表1。从中可以看出,在矩阵的信噪比为-10 dB及测试信号的信噪比为-5 dB的严重噪声条件下,BSCPO算法的定位精度最高。这表明,BSCPO算法在鲁棒性和定位精度方面优于其它6种机器学习算法,从而可说明DFL处理过程也较可靠。 表1 本文算法与其它机器学习算法的定位准确性的比较 3.2.3 多目标定位方法的性能 以两个目标定位为例,对本文BSCP多目标定位性能进行了评价。目标真实位置见表2所列的6种情况。 表2 6种情况下两个目标的真实位置分布 原始测试数据的定位结果如图9所示,可以从情况1到情况5准确地定位目标。在此以一个正确定位的块稀疏解为例,即情况1。对于情况6,网格23处的目标位于对角相邻的网格28处,这是不正确的,但是仍然接近正确的位置,而另一个目标可以正确地定位在网格25处,如图9(b)和图9(c)所示。这表明该算法在多目标定位中性能良好。 图9 多目标实验中的定位结果 为了解决传统的无源定位机器学习算法的缺点,提出了一种基于块稀疏编码的物联网环境下无源定位机器学习算法,并且通过数据集实验进行了验证,可以得出如下结论: (1)当无源定位系统受到严重噪声干扰时仍具有较好的鲁棒性能与恢复性能。 (2)由于充分考虑了群体结构信息,所以本文提出的BSCPO算法在定位精度优于其它算法。 (3)在原始感知信号中加入了严重的高斯噪声,既能够保护网络隐私,又提高了模型的鲁棒性。 但是,在现有的研究条件下,用户的隐私数据保护仍旧是急需解决的问题,下一步将研究如何在不泄漏真实数据的情况下更新矩阵的变量,从而达到分类与保护的效果。2 提出的方法
2.1 现存问题及本文提出的解决方案

2.2 块稀疏编码定位算法
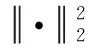


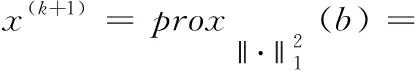
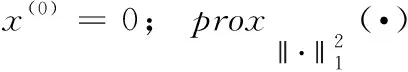
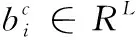
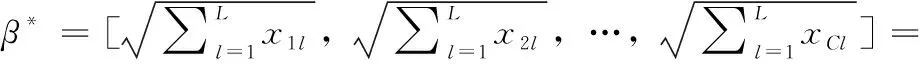


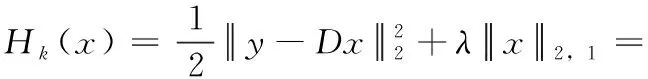
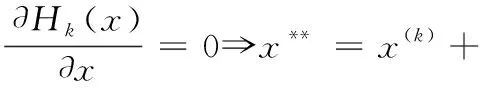
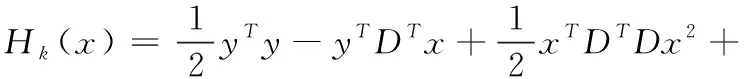
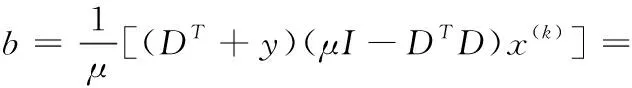
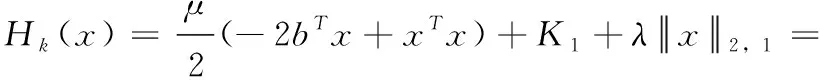
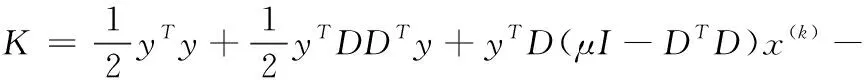
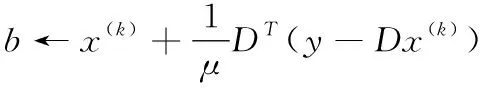
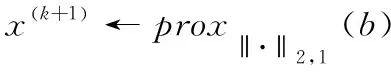
3 实验与分析
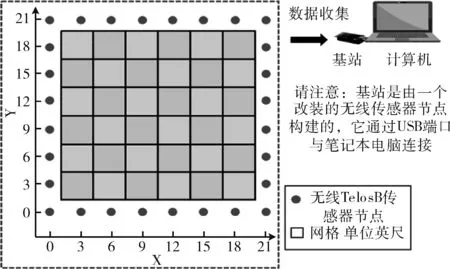
3.1 实验相关介绍
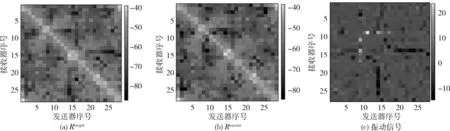
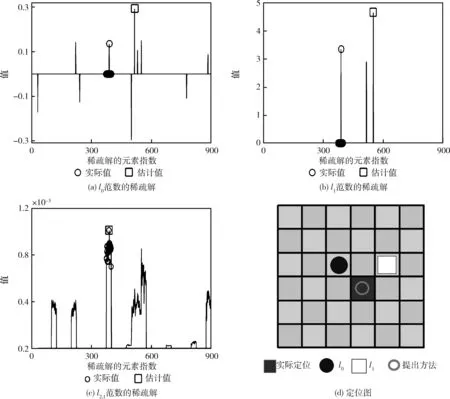
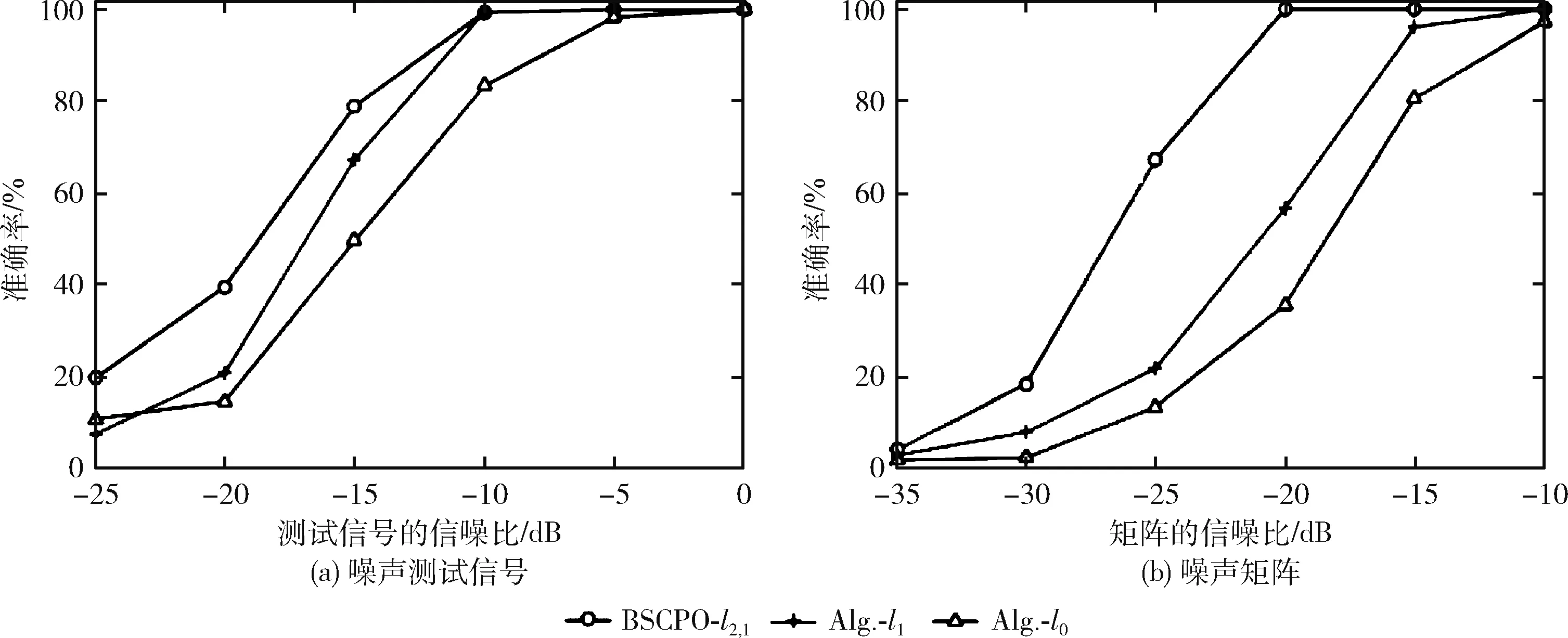
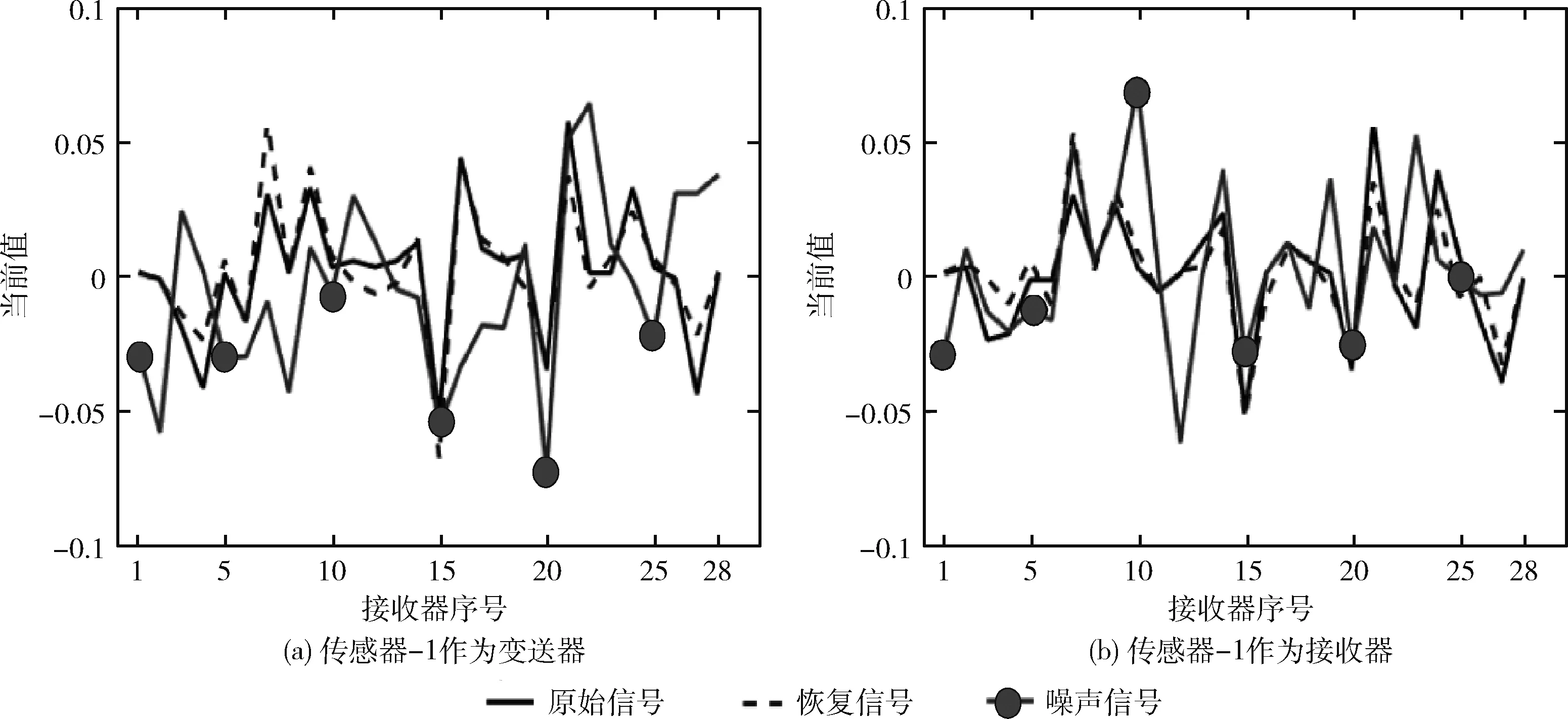
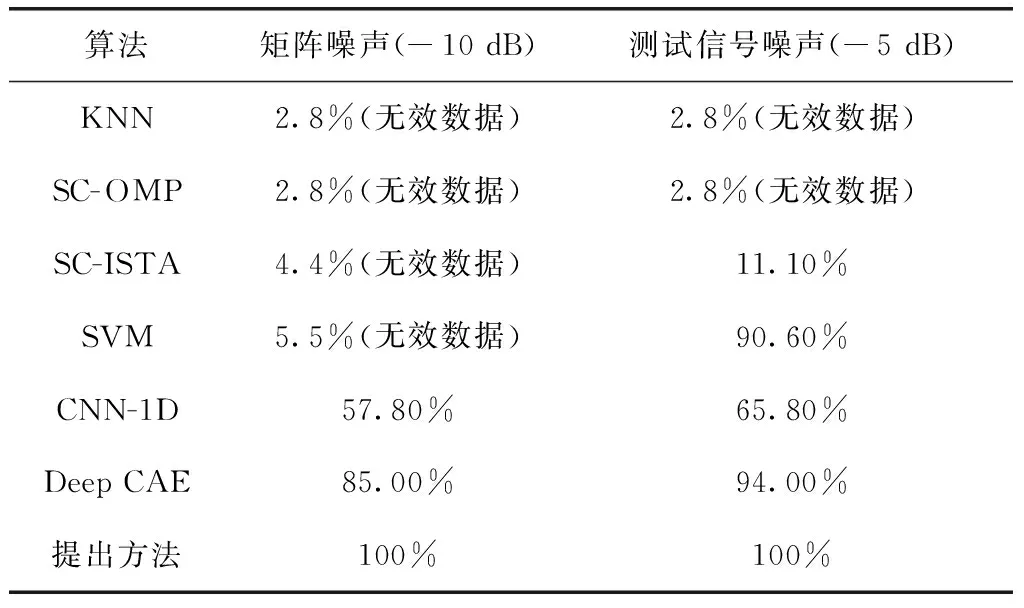
3.2 实验结果及分析
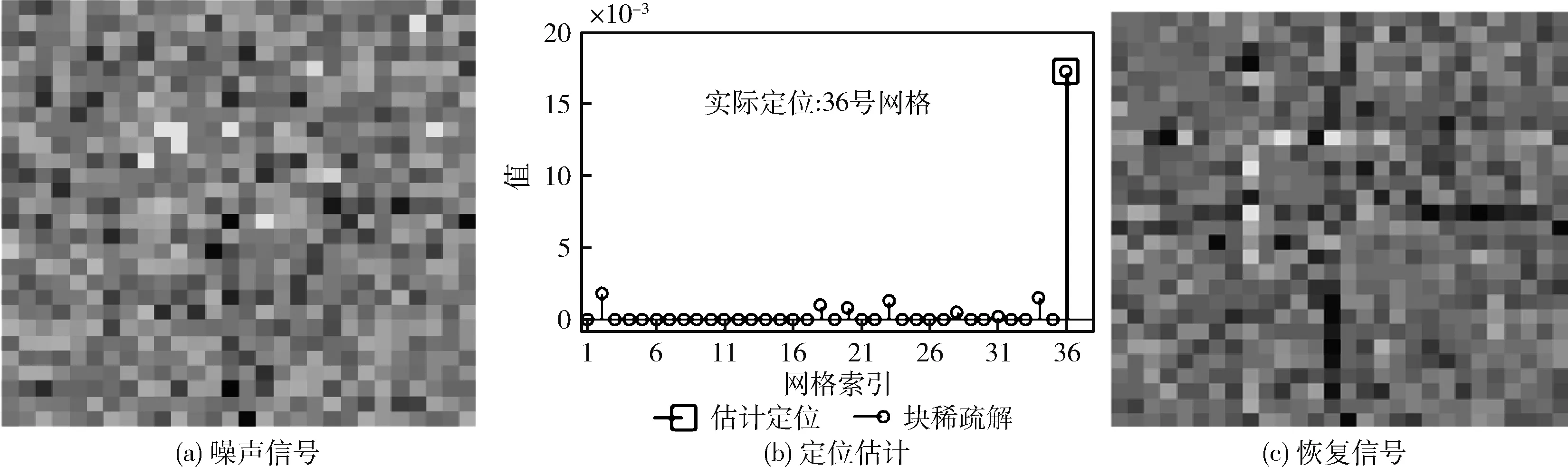
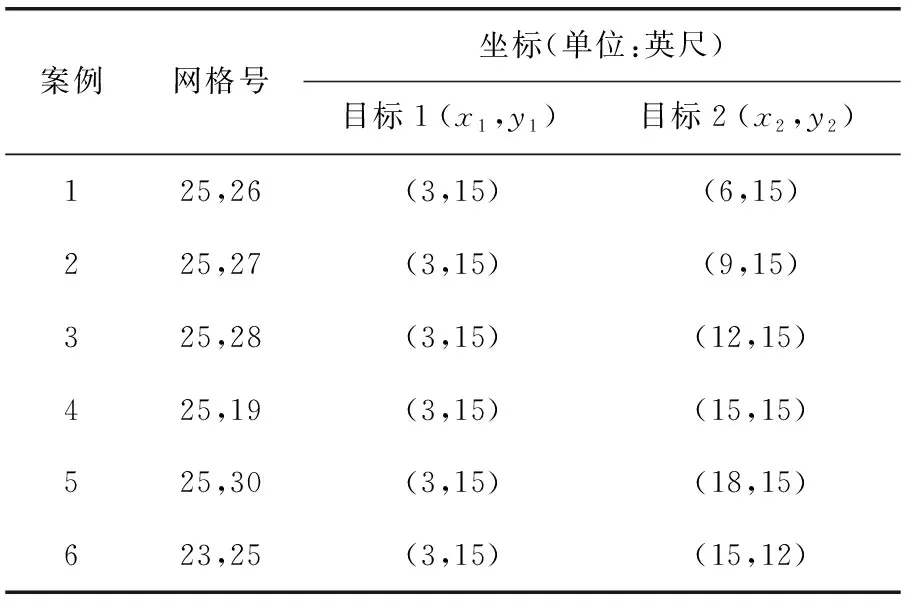
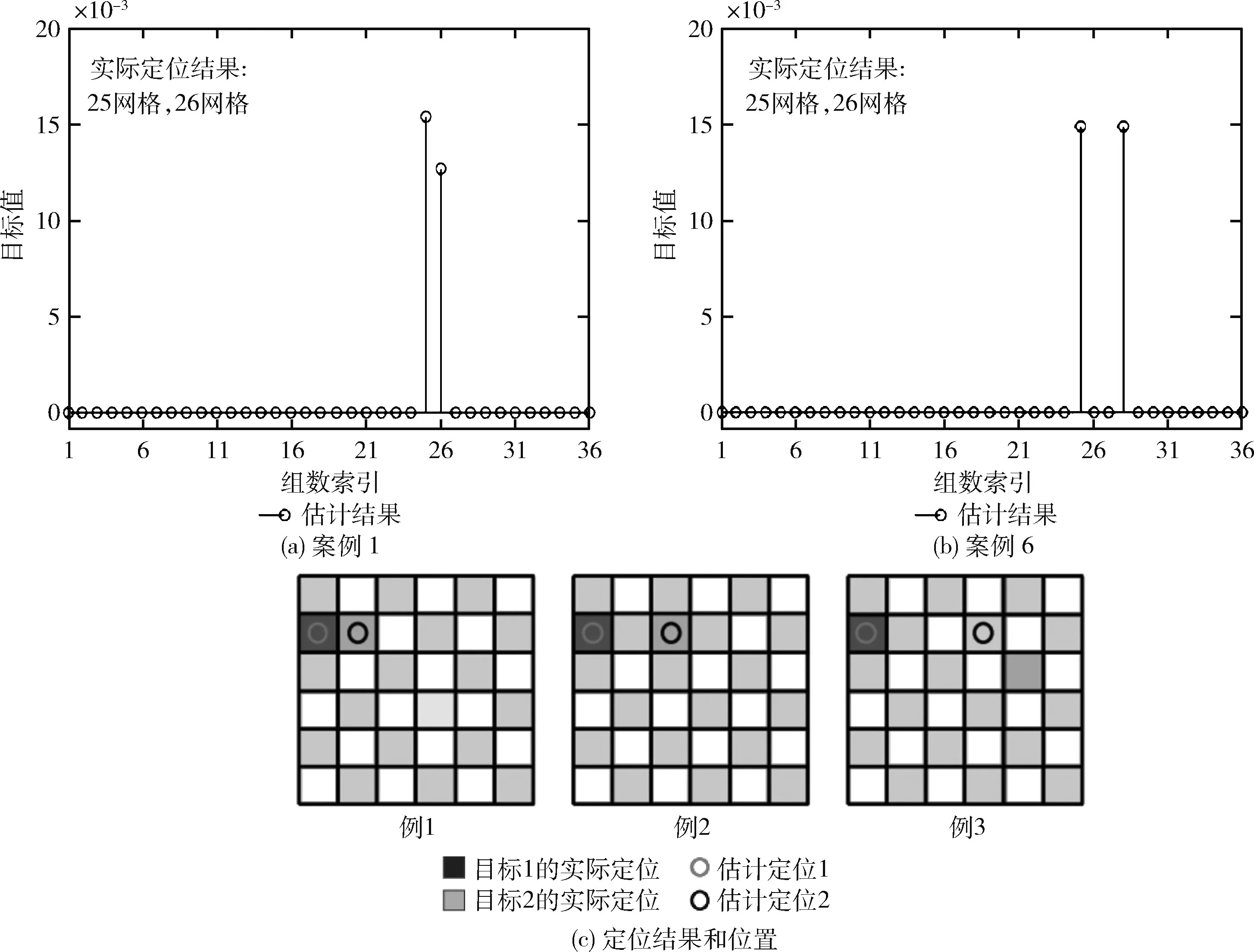
4 结束语
