面向边缘计算系统的隐私编码计算方案
2022-10-01昌继青储海波施连敏
昌继青,储海波,王 进+,沈 炯,施连敏
(1.苏州大学 计算机科学与技术学院,江苏 苏州 215006;2.苏州市公安局 大数据建设应用支队,江苏 苏州 215008)
0 引 言
传统的云计算模型由于集中式的存储特点与带宽资源限制已经无法满足计算任务的实时性和高效性需求[1]。在此背景下,边缘计算作为物联网设备和云数据中心之间的桥梁,开创了在网络边缘收集、处理数据的新型计算模式。边缘计算利用靠近数据源端的边缘设备为用户提供实时的数据处理服务,将云计算任务部分卸载到网络边缘以减轻云中心的计算、通信负载,已经成为新的研究热点[2]。虽然边缘计算能够有效缩短计算任务的完成时间且应用前景广阔,但由于边缘设备轻量化、分布式等特点,隐私安全和资源限制问题已经成为边缘计算发展过程中的两个巨大挑战。首先,边缘设备,如基站、移动终端、路由器、个人电脑等,通常存储、计算和通信资源有限。尤其,边缘设备有限的存储资源直接限制了它们可以执行的计算和通信任务数量。因此,如何充分利用边缘设备的有限资源,高效地完成计算任务值得深思。其次,不可信的边缘设备引起的隐私安全问题也亟需解决。边缘设备通常分散在用户侧,其分布式的特征导致边缘设备更容易被入侵者监视或攻击。在许多边缘计算应用场景中,例如智慧医疗、自动驾驶、附近影院推荐服务等,边缘设备可能从历史记录中推断出用户的隐私偏好,损害用户的隐私安全。因此,本文针对存储资源有限的边缘计算系统,设计了一种隐私编码计算方案(private coded computation scheme for edge computing system,PCEC),在保护用户隐私的前提下有效地降低了通信负载。PCEC方案给出了一个基于线性编码的计算方案,通过将目标数据与其它数据通过线性操作混合,使得边缘设备在计算过程中无法识别用户目标数据,同时降低通信负载。
1 相关工作
近年来,在边缘计算领域的学者们取得了许多优秀的成果。Li等[3]提出了一种通用的编码边缘计算方案将计算任务卸载到边缘设备,同时考虑计算负载的最小化以及通信效率的最大化。Zhou等[4]以矩阵乘法任务为例,利用空闲边缘设备进行分布式计算以降低计算延迟。越来越多的研究关注到了边缘设备的轻量化和分布式特征,思考如何充分利用有限的资源高效地完成任务。比如,Wang等[5]针对设备存储资源有限且存储容量各不相同的边缘系统,通过任务分配方案和编码计算方案的联合设计,最小化矩阵相乘任务中的总成本。Li等[6]提出了一个统一的分布式编码框架,并将其应用在雾计算系统中,实现了通信资源和计算资源之间的权衡。
此外,边缘计算中的安全问题,包括数据机密性和用户隐私性[7],也引起了学者的广泛关注。线性编码能够在保证安全的同时低带宽消耗和传输延迟[8],已经得到了广泛的应用。在数据机密性方面,许多文献已经提出了各种安全高效的编码计算方案并考虑了丰富的计算模型,例如同构边缘系统[9]、异构边缘系统[10]、“滞后节点”问题[11]、合作攻击模型[12]、主动攻击模型[13]等。然而保护用户隐私也具有现实意义却尚未得到充分的研究。针对用户隐私的保护,Sun等[14]通过将原始数据与其它信息进行混淆实现了隐私数据恢复。Mirmohseni等[15]提出了一种编码计算方案,利用设备帮助用户计算来自N台服务器的K条消息的任意函数,同时对每个设备隐藏该函数。在矩阵乘法任务中,Kim等[16]提出了一种基于多项式编码的计算方案,同时保护了数据机密性和用户隐私性。在以上隐私问题的研究中,计算设备需要存储整个数据,或者从远程公共数据库下载数据。这些方案带来了额外的存储要求和通信负载,不能直接应用于资源有限的边缘计算系统。因此,如何利用资源有限的边缘设备,在保护用户隐私的前提下高效地完成计算任务,成为研究的重点。
2 问题建模
2.1 系统模型
如图1所示,边缘计算系统模型通常由云、用户s0和n个边缘设备si组成,i∈{1,…,n} 且n≥2。 边缘中有一个由w个大小为r×s的矩阵组成的库B={B1,B2,…,Bw}, 且数据块Bj是B中的第j个矩阵,j∈{1,…,w},w≥2。 每个边缘设备最多存储t0个数据块,即t0为边缘设备的存储限制,t0>0。 用户拥有一个大小为m×r的本地矩阵A且仅想要使用B中的一个数据块计算得到ABθ,θ∈{1,…,w}。 用户隐私性要求任意一个边缘设备无法识别用户目标矩阵的下标θ。
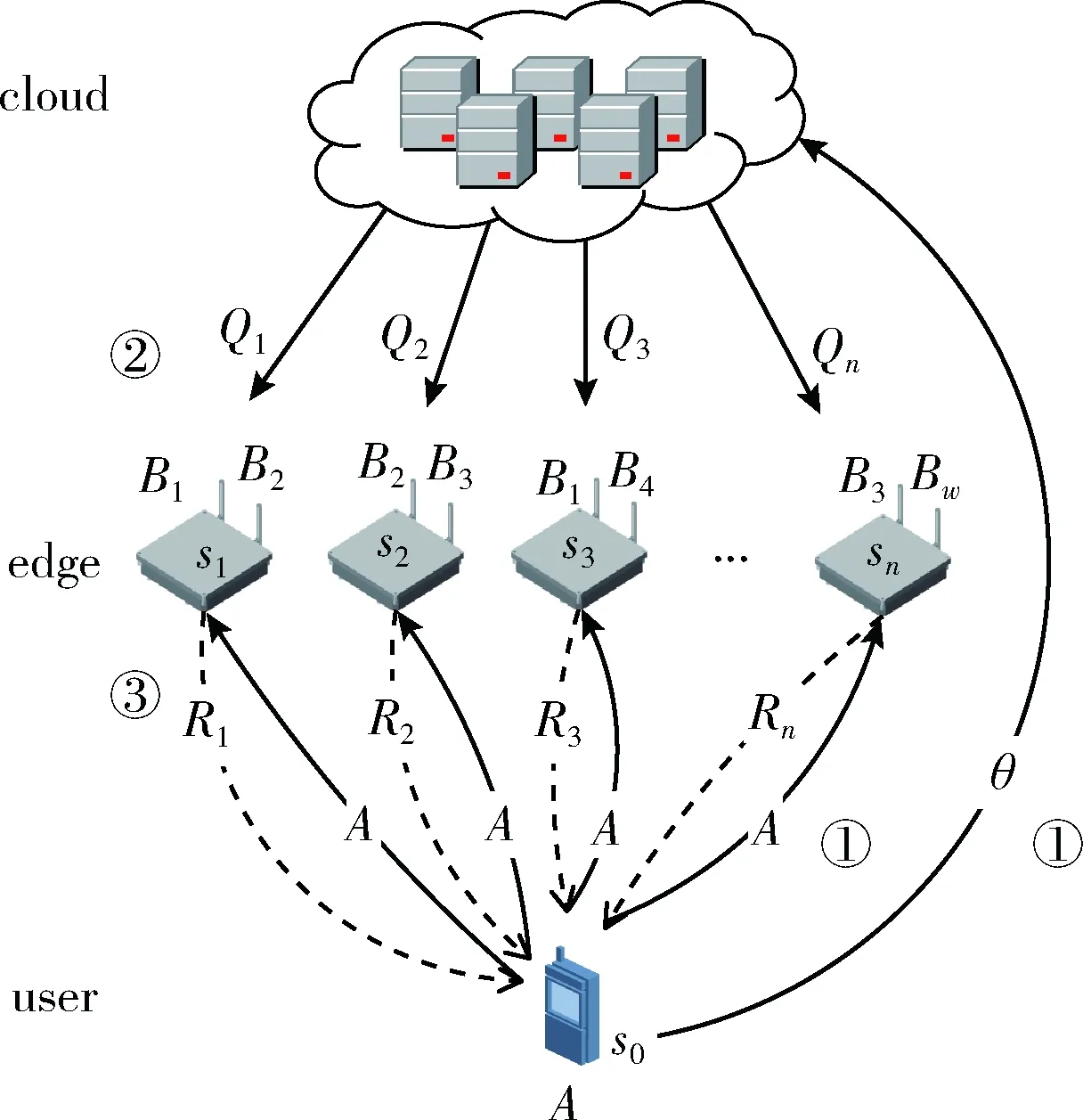
图1 隐私边缘计算的系统模型
2.2 计算框架

(.)[i,j]代表一个矩阵第i行第j列的元素,块矩阵相乘操作定义如下:
定义1 块矩阵相乘⊗:假定存在一个大小为e×f的矩阵Q和一个大小为g×h的矩阵F,Qu代表矩阵Q的第u行。按列将矩阵F分成f个层,其中Fv代表第v个层,那么执行块矩阵相乘操作后可以得到式(1)
(1)
然后,隐私计算流程如图1所示:
(1)用户将所需数据块的索引θ发给云,并将矩阵A分发给边缘设备。
(2)收到θ后,云会生成一个计算方案,包括一组编码系数矩阵Q={Q1,Q2,…,Qn}, 一个选择矩阵C和一个解码矩阵D。然后云把Q发送给边缘设备。
(3)在收到Qi和A后,边缘设备si开始执行计算任务。
1)si将存储的每个数据块按列分成l=αt个层后得到Fi= [M1,1…M1,lM2,1…M2,l…Mt,l]。
2)si计算Gi=Qi⊗Fi后进一步得到Ri=AGi并把结果返回给用户。Ri,u=AGi,u代表Ri中的第u个值。
(4)当接收到所有中间结果后,用户s0完成如图2所示的解码过程:
1)s0根据矩阵C选择Ri中有用的值并得到R′i。 具体来说,若C[i,j]=1, 用户选择Ri,j用于解码过程,并将它加入到R′i。h表示式(2)的值
(2)
2)s0计算得到R′=[R′1T…R′nT]T, 其中 (.)T代表矩阵转置。实际上,R′中共有h个值,其中的任意值都是来自集合 {ABj,v|j∈{1,…,w},v∈{1,…,l}} 中的h个层的线性组合。如果用一个大小为h的矢量x代表这些层,可以得到R′=Dx, 其中D是相应的编码矩阵。
3)s0可以解码R′=Dx得到x,并恢复出ABθ。
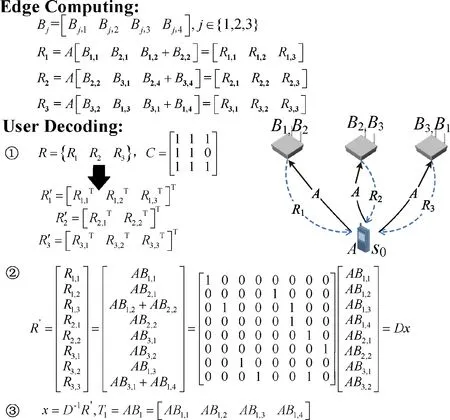
图2 解码示例
为评估所提计算方案,我们给出如下定义:
定义2 通信负载:边缘设备返回给用户的中间结果的大小,即所有中间结果对应的矩阵中的元素总个数。
2.3 攻击模型与隐私要求
本文研究了被动攻击模型,每个边缘设备均可能是被动攻击者,或者被攻击者窃听。这些被动攻击者相互不勾结,但不断窃听网络内的计算节点,试图从收到的数据包中破解出用户的信息。本文重点关注通信和数据计算过程中的隐私保护问题,当用户解码得到ABθ后,任意一个设备无法识别用户目标矩阵的下标,即θ。 类似的隐私条件已经在文献[14,16]中被研究过。因此,对边缘设备的隐私约束为:
定义3 隐私条件:当且仅当对任意i∈{1,…,n}, 边缘设备si均满足式(3)时,计算方案保证了用户的隐私安全
I(θ;Qi,A,Ri,Vi)=0
(3)
式中:I(·;·) 表示互信息,用于度量变量间共享的信息。式(3)表示边缘设备的获得数据Qi,A,Ri,Vi与θ相互独立,即无法从Qi,A,Ri,Vi中获得θ的任何信息。
3 隐私编码计算方案PCEC
本节给出PCEC的方案设计。同时我们对该方案进行理论分析,证明它满足了隐私条件且可以保证ABθ的恢复。
3.1 PCEC方案设计
本小节将从存储分配、隐私计算方案设计和边缘计算过程3个关键部分对提出的PCEC方案进行描述。
3.1.1 存储分配

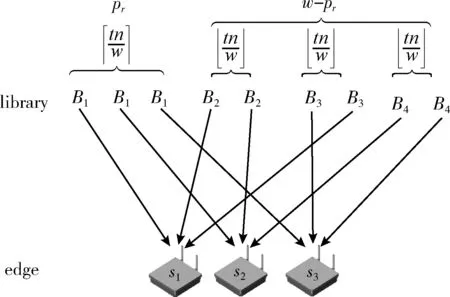
图3 存储分配示例

3.1.2 计算方案设计
为了便于计算方案的理解,我们先基于图2中的例子描述PCEC方案的大体思路,然后给出该方案的通用设计。
示例:在图2中的边缘计算部分,有n=3个边缘设备和w=3个数据块,每个边缘设备存储了t=2个数据块,每个块出现在α=2个设备中,用户想得到AB1。 在图2中节点返回的中间结果Ri中,目标数据块B1中的每个层要么单独出现,要么与在其它节点已经发送过的层组合出现。因此,在所有设备返回结果后,用户可以恢复出AB1。 此外,在s1返回的结果R1中,数据块B1和B2都使用了2个不同的层。同时其它2个节点返回结果的结构类似,且均使用了存储数据块的不同层。因此,这些边缘设备无法辨别哪一个数据块是用户的目标。在以上例子中我们发现,可以对返回结果设计通用的数据结构,以保证每个数据块被使用相同的次数。同时,随机选择使用的层的顺序可以进一步保证用户的隐私性。
通用设计:首先为每个设备返回的结果设计通用的消息结构,然后用设备存储的数据来具体地实例化该消息结构。

表1 t=2,α=2时消息结构示例

表2 t=3,α=3时消息结构示例
(2)实例化:接着我们用每个节点存储的层来对消息结构进行实例化。为了隐私安全,PCEC方案需要生成一个大小为w×l的随机矩阵P来实现层的随机选择。具体地,第v次从Bj中选取一个层时,该方案将选择B′j=Bj,u,u=P[j,v]。 因此在Bj中随机选择层,相当于在B′j中顺序选择层。首先,每个层在每个边缘设备中不会被重复使用。其次,在所有边缘设备中,按升序原则使用B′θ的所有层。第三,对于其它数据块中层的选择必须遵循3条规则:首先,在所有边缘设备的1-sum中,按升序原则使用层。第二,在每个边缘设备中,按升序原则使用与B′θ一起出现的层。第三,在每个边缘设备中,按降序原则使用层。这3条规则由强到弱。以上规则可以保证PCEC最后能恢复出ABθ。
3.1.3 边缘计算过程
在收到Qi和A后,边缘设备si开始执行计算任务。首先,si将存储的每个数据块按列分成l个层后得到Fi。 然后si计算Gi=Qi⊗Fi。 注意计算过程相当于把不同的层通过加法组合在一起,即实现隐私计算方案设计中消息结构和实例化过程。最后,si计算Ri=AGi并把结果返回给用户。
3.2 理论分析
3.2.1 隐私性证明
定理1 PCEC方案满足隐私条件。
证明:根据链规则,将式(3)中的隐私条件转化如下
I(θ;Qi,A,Ri,Vi)=I(θ;Qi)+I(θ;Vi|Qi)+
I(θ;A|Qi,A,Vi)+I(θ;Ri|Qi,Vi,A)
(4)
首先,用户的本地数据A与θ无关,因此I(θ;A|Qi,A,Vi)=0。 同时存储分配阶段生成的设备存储的数据Vi和Fi也与θ无关,即I(θ;Vi|Qi)=0。
由PCEC的设计过程可知Qi由消息结构和实例化过程决定。其中消息结构的设计完全与θ无关。此外,实例化过程相当于从数据块中选择不同的层。对于每个设备存储的数据块Mb,实例化过程选择了αt-1个不同的层,b∈{1,…,t}, 设ob={ob,1,…,ob,αt-1},b∈{1,…,t} 为这些层的下标。ob,u实际上是随机矩阵P中的一个值,u∈{1,…,αt-1}。 因此{ob|b∈{1,…,t}} 中的元素相互独立且与θ无关。所以可知I(θ;Qi)=0。 由于Ri由A,Fi和Qi决定且它们均与θ无关,因此可得I(θ;Ri|Qi,Vi,A)=0。
综上,对任意边缘设备si,I(θ;Qi,A,Ri,Vi)=0均成立,即PCEC满足隐私条件。
3.2.2 可解码性证明
定理2 当 (α-1)t-1≥αt-2且α≥2时,PCEC方案可解码出ABθ。
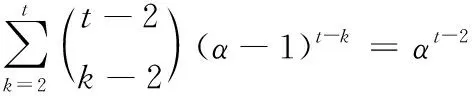
用z1代表第二种形式中的所有层的最大下标值。我们假设z1>p。 在PCEC方案选择层Mu,z1之前,如果第三种形式中的所有层的下标均大于p,那么为前二种形式选择层时,PCEC方案可以选择 {Mu,z|z∈{1,…,p}} 中的任意层。同时,由于前二种形式中只需要p个层,并且第二种形式中的层按照升序原则选择。因此可知z1≤p, 但这与z1>p相矛盾,所以第三种形式中必然存在一个层Mu,z2满足z1>p≥z2。 当我们为第三种形式选择Mu,z2时,Mu,z1尚未使用,然而我们选择了小于z1的z2, 这与按照降序原则选择层相矛盾。因此,假设不成立,即z1≤p且第二种形式中的所有层的下标均不大于p=αt-2+(α-1)t-1。
在消息结构中,每种类型的1-sum由一个单独的层构成,且出现(α-1)t-1次。所以,对于每个设备中存储的每个数据块Mu, 我们可以直接获得 (α-1)t-1个层。同时由于至少α个设备存储了该数据块,我们可以从1-sum中直接获得α(α-1)t-1个层。在每个边缘设备的1-sum中,任意非目标数据块Mu遵循降序原则选择层,因此用户可以得到数据 {AMu,v|v∈{1,…,α(α-1)t-1},Mu≠Bθ}。 当 (α-1)t-1≥αt-2,α≥2时,可得α(α-1)t-1=(α-1)(α-1)t-1+(α-1)t-1≥αt-2+(α-1)t-1=p, 即对于任意非目标数据块Mu, 用户可以直接得到 {AMu,v|v∈{1,…,p},Mu≠Bθ}。 在消息结构中,Bθ中的每个层要么单独出现要么与已经发送过的非目标块的层一起出现。因此,在PCEC方案中,当每个设备返回中间结果给用户后,用户可解码出ABθ。
4 仿真结果与分析
4.1 环境和参数设置
本文实验的硬件环境为Intel Core i5-6400 CPU,8 GB内存。我们使用Java语言进行编程实现存储方案,通过大量实验计算得到不同参数下,不同方案的通信负载。同时我们利用Matlab绘图工具,绘制相关实验图,以此验证提出方案的性能。我们考虑以下3种参数:①库B中的矩阵数量w;②边缘设备的数量n;③边缘设备的存储限制t0。参数的默认值为:m=1000,s=1000,n=20,w=15,t0=w/2。 对于每个参数组合,我们为每个方案生成100个实例,并报告平均结果。我们将本文的PCEC方案与以下方案比较:
(1)无编码的隐私计算(uPC)方案:所有边缘设备直接计算用户本地数据A和节点存储的所有数据块的乘积,并将中间结果返回给用户。该方案中用户无需解码,可以直接从中间结果中得到ABθ。 注意此时,若每个节点均只存储2个数据块,该方案通信负载最小为2n。
(2)基于分块的隐私计算(BPC)方案:该方案利用简单的分布式计算原理,首先将Bθ按列进行分块,然后把计算ABθ的任务分散到所有存储了Bθ的节点上,即让这些节点各自完成一部分子任务。为了保证用户隐私,所有设备除了计算ABθ的子任务外,还需要额外计算A和它们存储的其它非目标数据块的乘积,并将结果返回给用户。
(3)基于范德蒙矩阵编码的隐私计算(VPC)[16]方案:每个边缘设备将存储的矩阵按列分成块α后使用范德蒙矩阵进行编码。然后,每个设备将结果与A相乘,并将乘积返回给用户。注意,当返回的总中间结果数量αn不小于未知数的数量αw时,该方案才能实现顺利解码出ABθ。
4.2 计算方案的性能
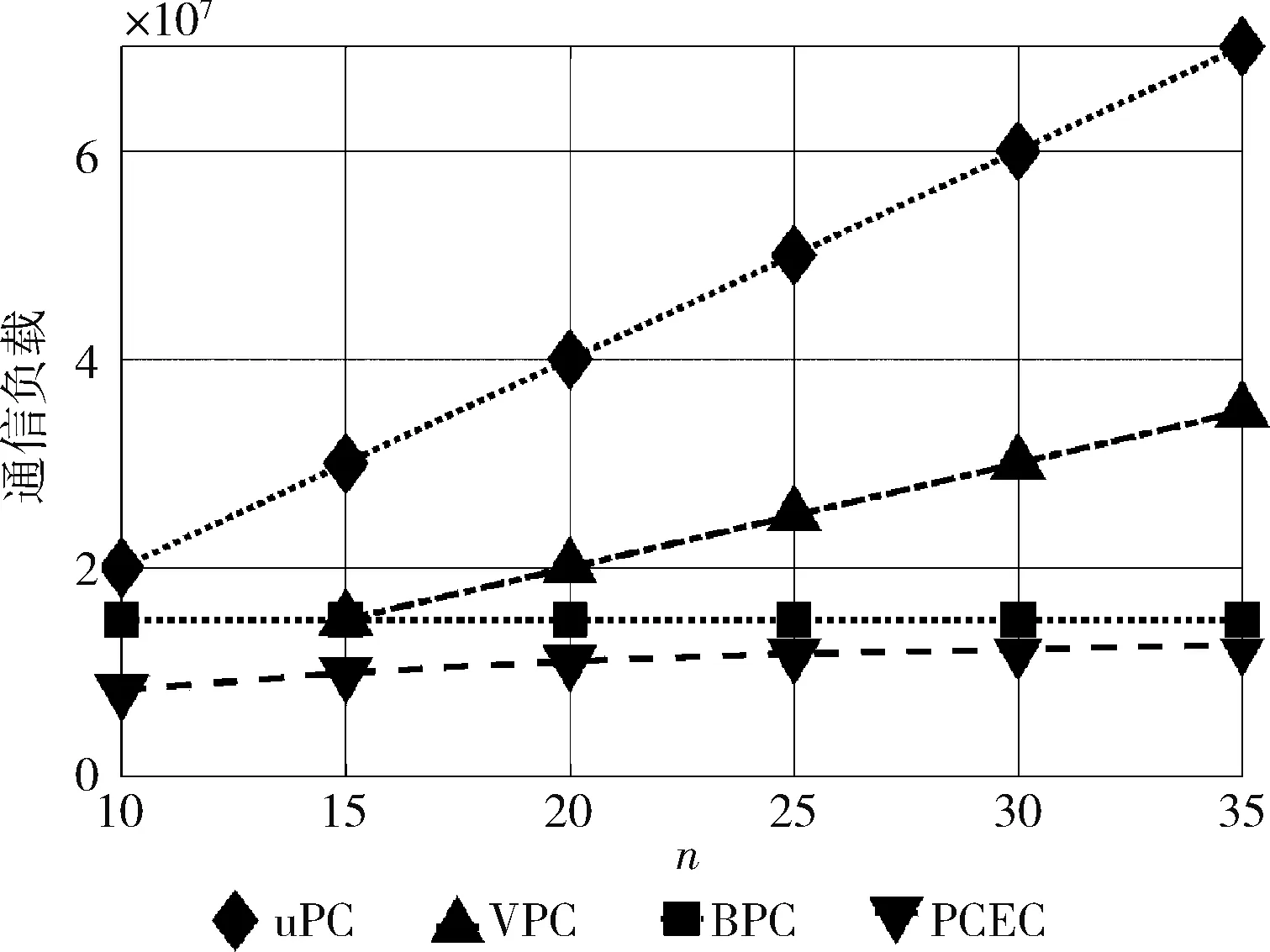
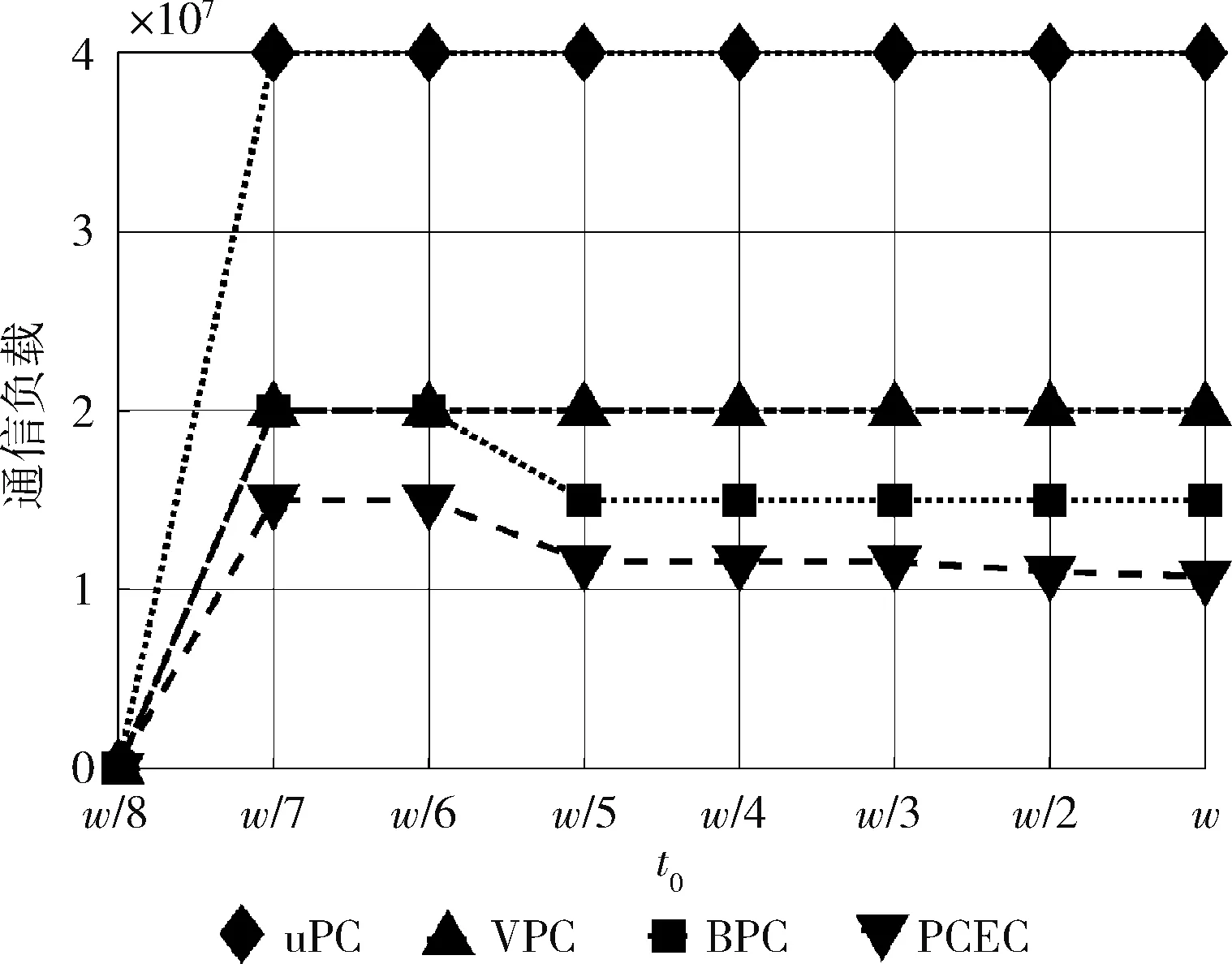
我们将比较4种方案的通信负载与在不同参数下的变化情况。首先分析通信负载与库中的矩阵数量w的关系。当n为20个边缘设备时,4种方案的通信负载的变化情况如图4所示。从图4中可以看到,当w从5变为30时,BPC和PCEC的通信负载随着w的增加而增加。这是因为当w增加时,BPC和PCEC中的边缘设备需要将目标矩阵的数据与更多不同矩阵的数据混淆,导致通信负载增加。而uPC或VPC的通信负载与w无关。这是由于uPC可实现的最小通信负载是2n,与w无关。此外,我们还发现:①PCEC的性能优于BPC(减少了约30%的负载)、VPC(减少约35%的负载)、uPC(减少75%的负载);②在n 图4 通信负载与w关系 然后我们分析通信负载与边缘设备数量n的关系。当w为15个矩阵时,4种方案的通信负载的变化情况如图5所示。从图5中可以看到,uPC和VPC的通信负载随着n的增加而线性增加。这是由于更多的节点存储了更多的数据,需要返回的数据也相应变多。其次我们发现,PCEC中通信负载的增加缓慢,几乎可以忽略不计。这是由于PCEC中,当节点数量增加时,每个数据将被存储更多次,数据矩阵的分层数变多且每一个中间结果变小,因此总的通信负载增加比较缓慢。此外,BPC的通信负载与n无关。这是因为BPC要求存储Bθ的边缘设备计算ABθ的一部分。如果有更多的边缘设备,每个边缘设备将承担更少的计算任务。因此BPC的总通信负载主要取决于w的大小。相比较而言,PCEC总是能够很好地减轻n的变化带来的影响,并实现最少的通信负载。 图5 通信负载与n关系 最后,我们分析通信负载与存储限制t0的关系。在图6中,系统中存在n=20个边缘设备和w=15矩阵。通过将每个设备的存储限制t0从w/8增加为w,我们比较了4种方案的通信负载。注意,当t0≤w/8时,有t0<2, 即每个设备最多只能存储1个数据块。而本文不考虑这种情况下的隐私问题,所以默认每个方案的通信负载为0。从图6中可知,uPC的通信负载较大,且基本不变。这是由于uPC可实现的最小通信负载是2n,与t0无关。其次,当t0从w/5增加为w/2时,每个方案的通信负载只有不明显的降低。因此,在实际应用中我们可以选择存储能力有限的节点完成隐私任务,将存储资源相对丰富的节点投入到更复杂的计算任务中,可以保证通信负载基本不变的前提下,提高节点的利用率。最后,我们发现BPC和PCEC的通信负载随着t0的增加而有所减少,且PCEC始终实现了最低的通信负载。因此,本文提出的方案能够充分利用边缘设备存储资源有效地节约通信成本。 图6 通信负载与t0关系 本文主要研究了在一个资源有限的边缘计算系统中,如何高效地完成计算任务并保证用户的隐私安全的问题。针对上述问题,提出了一种面向边缘计算系统的隐私编码计算方案,通过设计基于冗余的存储方案以及基于线性编码的计算方案,能够充分利用边缘设备的存储资源,解决边缘计算中的隐私保护问题,并降低通信负载。最后,通过设计实验对所提PCEC方案进行了分析评估。实验结果表明,与其它方案相比,PCEC能够有效地减少约75%的通信负载。在下一步工作中,我们将利用现实的边缘计算系统验证所提出的方案,并考虑异构边缘计算系统中的隐私保护问题。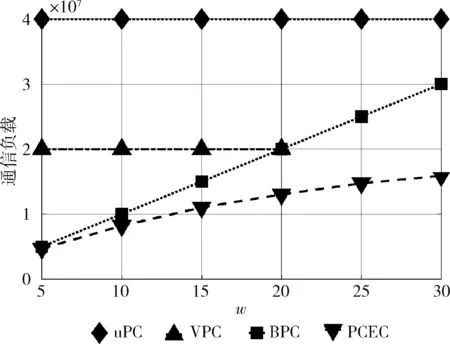
5 结束语
