基于概念本质 实现有效建构
——人教版教材四年级上册“平行和相交”教学思考与实践
2022-10-01鲁洁
□鲁洁
【课前思考】
“平行”是人教版教材四年级上册“平行四边形和梯形”单元的核心概念之一,是认识平行四边形和梯形的基础。教材将“平行”与“垂直”这两个核心概念安排在同一课时进行教学,实际教学效果如何?笔者对城区某校223名四年级学生进行了教学后测,情况如表1。

表1
从后测情况看,学生的“垂直”概念建立得比较好,有93.3%的学生能在魔方上找出与已知线段垂直的4条线段。“平行”概念的建构存在欠缺,有79.8%的学生找不到“看不见”的平面上的平行线。另外,学生对两线位置的关系不清晰,仅有54.7%的学生能将“相交、平行、垂直”三者的关系表达正确。造成以上结果的原因分析如下。
在本节课的学习之前,学生已经认识了直角、长方形和正方形,这些都是学生学习“垂直”概念的知识基础,而对于“平行”概念的学习缺少必要经验的支撑,所以“平行”概念的建立较“垂直”相对困难些。
教师往往按照教材编排将“平行”和“垂直”安排在同一课时教学,但由于一节课的时间有限,学生对“平行”和“垂直”这两个概念的理解仅仅停留在外延判别上,对它们的本质意义不能牢固建立,特别是对本单元的核心概念“平行”的前置条件“同一平面”的理解不深刻,导致“平行”概念建构不到位,同时对“相交”“平行”“垂直”三者的逻辑关系辨认不清。
基于以上分析,将“平行”与“垂直”安排在同一课时学习,效果不佳。而“平行”这一核心概念又是后续学生学习平行四边形和梯形、画长方形等的基础。为了进行基于核心概念的单元整合教学,笔者对学习序列进行了调整,把“平行和相交”单独设为一课时,这样更利于学生建构“平行”这一核心概念,从而达成以下教学目标。
(1)通过想象、分类等活动,理解“平行”的意义,能正确判断平行现象。
(2)经历画一画、数一数、辨一辨等活动,感悟“同一平面”,发展“平行”的空间意识,积累活动经验。
(3)结合对生活中平行现象的辨认,感悟“平行”与生活的联系。
【教学实践】
一、在分类中感知“平行”
(一)通过想象,唤醒经验
教师引导学生进行两次想象:第一次把黑板想象成一个平面;第二次想象在这个平面上出现了一条直线(大屏幕上显示一条直线)。
师:你们想的直线和大屏幕上的一样吗?
生:方向不一样,我想象它是横的。
生:和我想的位置不一样。
生:长短不一样。
生:直线可以向两端无限延伸,所以不能比长短。
(二)通过分类,认识平行
教师让学生先想象两条直线的位置关系,然后在白纸上把它们画下来。随后选择有代表性的作品进行展示(如图1)。

图1
教师引导学生先观察展示作品,再独立思考进行分类,然后同桌之间讨论,最后再全班交流讨论。
生(第1组代表):我们组按两条直线是不是交叉来分,①⑤是交叉的,其余是不交叉的。
师:交叉是什么意思?大家用手比画一下(全体学生比画)。你们说的分叉,在数学上我们称为这两条直线相交。
生(第2组代表):我们组认为③和⑥其实也相交,延伸一下就可以了。
生:是的,画一画就可以发现它们是相交的(学生在黑板上演示)。
生:不画也行,想象一下也可以发现它们是相交的(学生用手比画)。
生(第1组代表):哦,现在我们明白了,③和⑥看似不相交,其实是相交的。
生(第3组代表):我们组的想法和第2组一样,①③⑤⑥都是相交的,②④⑦是不相交的。
生(第4组代表):是的,我们组也认为②④⑦再延长也不会相交,因为它们的方向相同。
师:在同一平面内,两条直线的位置关系可以分为相交和不相交这两类,像②④⑦这样,两条直线永不相交我们称为这两条直线互相平行。
二、在量化中理解“平行”
(一)借助方格纸量化“平行”
让学生先独立在方格纸上画一条直线,使它与已知直线a平行。然后,教师选择有代表性的作品进行展示(如图2),并组织全班交流。
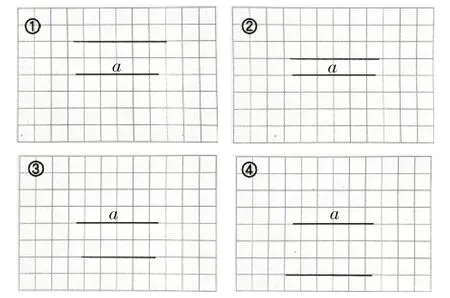
图2
师:观察这些作品,你发现了什么?
生:它们都是平行的。
生:有些画在已知直线的上面,有些画在下面。
生:它们都把直线画在了方格线上。
生:因为方格线和方格线是互相平行的,所以画在方格线上就行了。
生:我还发现画在方格线上两条直线的距离不变。
生:是的,在①号作品中,两条直线之间的距离是2格。
师:真是这样吗?我们一起来看看。
(课件动态演示:依次出现虚线。如图3)

图3
生:两条直线之间相距2格,直线延长后也相距2格。
生:是的,②号作品两条直线之间相距1格,④号作品两条直线之间相距3格。只要画在方格线上,相距的格子数就相等。
生:我觉得不一定要画在方格线上。把它向上平移一点点也可以。
(学生用手比画,教师用课件演示)
生:向下平移也可以。
(学生用手比画,教师用课件演示)
生:这样的直线能画无数条。
师:为什么刚才两位同学都提到要“平移”呢?
生:因为只有平移才能保证两条直线间的距离相等。
师:是啊,只有两条直线间的距离相等,它们才永远不会相交,互相平行。借助方格纸,同桌互相检查一下刚才画的直线是否和已知直线平行。
(二)利用变式加深理解
1.在运动中发现本质
教师用课件演示:将图3这组平行线按顺时针方向旋转90度(如图4),再旋转45度(如图5),引导学生判断这两条直线是否仍然平行。

图4

图5
生:仍然互相平行。
生:因为两条直线相隔的格数不变,永远不会相交,所以仍然平行。
师小结:像这样两条直线之间相隔的方格数相等,这两条直线就互相平行。
2.在调整中沟通联系
教师用课件出示作品(如图6),先引导学生辨析这两条直线是否平行,然后试着调整其中一条直线的位置,使这两条直线互相平行。

图6
生:这两条直线是相交的。
生:是的,是相交的。两条直线延长后有相交的点。
(教师用课件演示,如图7)

图7
师:怎么调整才能使这两条直线互相平行?
(先让学生想象比画,教师再用课件动态演示)
小结:两条直线互相平行时,两条直线之间的距离也处处相等。
(三)规范记法与读法
为了描述方便,我们给这两条直线标上字母ɑ,b。ɑ和b互相平行,还可以说ɑ是b的平行线或b是ɑ的平行线。记作:ɑ∥b。读作:ɑ平行于b。
三、在辨析中内化“平行”
(一)运用概念,寻找“平行”
教师出示图8,让学生找出每个图形中哪两条线段互相平行。

图8
让学生列举生活中有关平行的现象。
(二)观察思考,建构“同一平面”
教师先引导学生观察饼干包装盒的正面,找一找哪两条线段互相平行(学生找到后,教师用细铁丝标注出其中一组,如图9);接着教师打开盒盖(如图10),引导学生判断这两条直线是否还互相平行,并说明理由;最后教师撕破盒盖(如图11),组织学生讨论:“这两条直线是否还互相平行?请判断并说明理由。”

图9

图10

图11
师:图11中,这两条直线互相平行吗?
生:还是互相平行,因为它们没有相交。
生:不对,虽然这两条直线不会相交,但方向不一样了。(边说边比画)
生:我同意,如果把盒子竖起来,从上往下看,这两条直线没有对齐。(复原包装盒)这样对齐就可以了。
生:我知道了,它们在同一个平面内,才互相平行(边说边用手比画平面)。
师:刚才两条直线分别在哪个平面内?(引导学生分别比画两条直线所在的平面)
师生归纳得到:在同一个平面内不相交的两条直线叫作平行线。
(三)应用拓展,深化“平行”
1.在双杠模型中找“平行”
教师先引导学生同桌合作在双杠实物模型(如图12)中找平行线,并记录下来,然后组织交流。

图12
生:我们组发现了5组,分别是AB∥CD,CD∥GH,GH∥EF,EF∥AB,AC∥EG。
师:大家想象一下每组平行线所在的平面,并用手比画一下每组平行线所在的平面。
生:我们组发现还有2组,分别是AB∥GH,CD∥EF。
生:是的,我们组也找到了这2组。(借助双杠实物模型比画这两组平行线所在的同一平面)
生:你看,这样更明显(边说边用白纸物化平面)。
教师用课件演示7组平行线,配合出示每组平行线所在的平面。
2.在《几何原本》中找“平行”
教师介绍《几何原本》中关于“平行”的描述:“平行直线是在同一个平面内向两端无限延长不能相交的直线。”
【教学反思】
“平行”是本单元的核心概念之一,是认识平行四边形和梯形的基础。学生是否理解“平行”的概念本质,将直接影响他们后续进一步的学习。
一、遵循规律,关注概念建构的进度
概念的建构过程一般可分为“感知对象、建立表象、抽象本质、符号表征和概念内化”这几个阶段,本节课的教学既遵循学生的认知规律,又关注“平行”这一概念的发生、发展过程。主要安排了三个教学环节(如图13),先让学生在分类中感知“平行”,建立“平行”概念的表象;再借助方格纸让学生在量化中理解“平行”,使抽象的“平行”概念具象化;最后借助饼干盒、双杠模型让学生在辨析中内化“平行”,突破“同一平面”这一概念建构的难点。这样的环节安排遵循了概念建构的规律,紧扣概念内涵步步深入,使“平行”概念在学生头脑中有了从直观到抽象的完整建构过程。

图13
二、由表及里,获得概念感悟的力度
“平行”概念比“垂直”概念更为抽象,理解“永不相交”对四年级学生来说比较困难,它不像“垂直”概念可用直角进行直观判断。因此,在教学实践中,笔者借用方格纸让学生通过画一画、比一比、数一数等活动发现“两条直线间的距离(方格数)不相等,两条直线就相交;两条直线间的距离(方格数)相等,两条直线就互相平行”,引导学生从量化的角度直观地理解两条直线“相交”和“不相交”,对“平行”的概念通过“两条直线间的距离(方格数)相等”进行直观感知,由表及里,从而加深对概念本质的理解。
三、步步为营,达到概念理解的深度
调整课时后,学生对“平行”概念的建构过程是层层推进的。从基于“方向相同”的初步感知,到“距离相等”的直观感悟,再到“同一平面”的前置条件增加,不断完善认识,加深理解。教师借助饼干包装,“破坏”同一平面,从而让学生感受到两直线平行必须在同一平面内的必要性;利用双杠实物对“同一平面”进行直观物化,有效突破教学难点。
